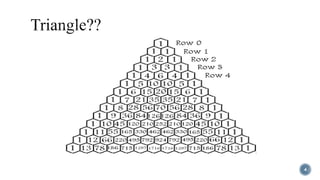
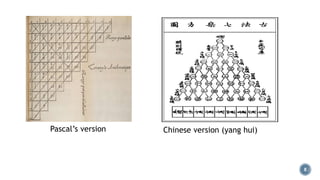
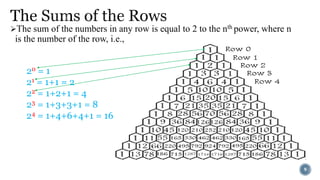
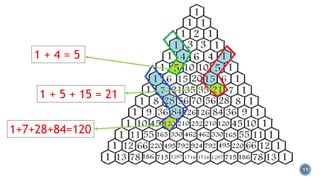
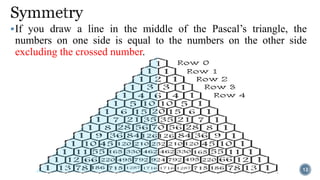
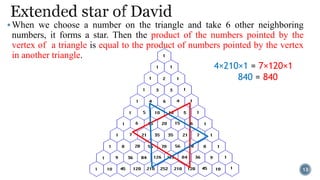
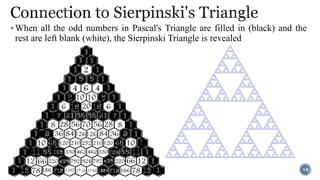
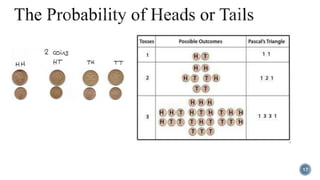
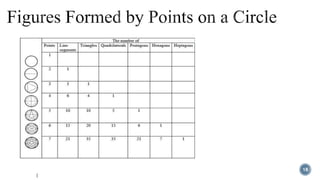
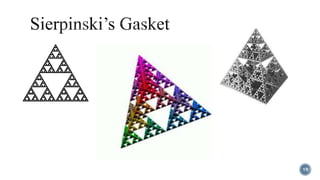
Pascal's Triangle is a triangular array of binomial coefficients named after mathematician Blaise Pascal, although it was studied by others prior to him. It has historical significance, being known in China as early as the 11th century and later presented by Yang Hui, while it has various mathematical properties and applications, including connections to probabilities and number patterns. The triangle reveals intricate patterns, such as the Sierpinski triangle when odd numbers are highlighted.

1. Pascal’s Triangle
1
Presented by: The Camouflage
Gagan Puri
Rabin BK
Bikram Bhurtel

2. Introduction and history
Properties
Application
References
2

3. It is a triangular array of the binomial coefficients
It is named after a French Mathematician Blaise Pascal
Although other mathematicians studied it centuries before him in
India, Persia (Iran), China, Germany, and Italy.
3

4. 4

5. If we expand (X+Y)n then we will get the numbers of n row of
Pascal’s triangle
Let’s see:
5

6. The Pascal’s Triangle is made up of the powers of 11, starting with
110. For nth row  11n
Or from the binomial expansion
Or trace this pattern:
Row 0
6

7. Pascal's triangle was known in China in the early 11th century
through the work of the Chinese mathematician Jia Xian
But it was presented in 13th century by Yang Hui
Hence it is still called Yang Hui's triangle in China.
The book was written in AD 1303 which is more than 700 years
ago and also more than 300 years before Pascal discovered it.
Because Pascal collected several results known about the triangle,
and employed them to solve problems in probability theory, it was
named after him
7

8. Pascal’s version Chinese version (yang hui)
8

9. The sum of the numbers in any row is equal to 2 to the nth power, where n
is the number of the row, i.e.,
9
20 = 1
21 = 1+1 = 2
22 = 1+2+1 = 4
23 = 1+3+3+1 = 8
24 = 1+4+6+4+1 = 16

10. If a diagonal of numbers of any length is selected starting at any of
the 1's bordering the sides of the triangle and ending on any number
inside the triangle on that diagonal, the sum of the numbers inside
the selection is equal to the number below the end of the selection
that is not on the same diagonal itself.
10

11. 11
1 + 4 = 5
1 + 5 + 15 = 21
1+7+28+84=120

12. If you draw a line in the middle of the Pascal’s triangle, the
numbers on one side is equal to the numbers on the other side
excluding the crossed number.
12

13. When we choose a number on the triangle and take 6 other neighboring
numbers, it forms a star. Then the product of the numbers pointed by the
vertex of a triangle is equal to the product of numbers pointed by the vertex
in another triangle.
13
4×210×1 = 7×120×1
840 = 840

14. When all the odd numbers in Pascal's Triangle are filled in (black) and the
rest are left blank (white), the Sierpinski Triangle is revealed
14

15. 15

16. 16

17. 17

18. 18

19. 19

20. 20

21. 21

22. References:
 https://www.slideshare.net/ecooperms/pascals-triangle-slideshow
 https://www.slideshare.net/rishabhbhndr1/pascal-triangle-36885431
 https://www.tutorialspoint.com/learn_c_by_examples/pascals_triangle_progr
am_in_c.htm
 http://britton.disted.camosun.bc.ca/pascal/pascal.html
 https://www.google.com.np/search?q=pascal+triangles&source=lnms&tbm=
isch&sa=X&ved=0ahUKEwiPntvH1avUAhVEQ48KHSOQC3QQ_AUIBig
B&biw=1517&bih=698#imgrc=Vnu3EO26ABcNxM:
22

23. Queries
23