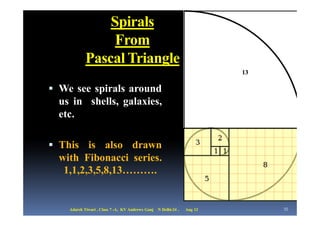
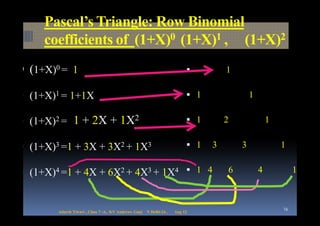
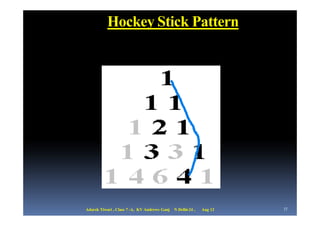
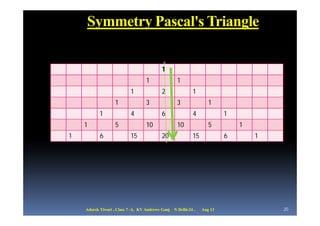
The document discusses Pascal's triangle, which was invented by French mathematician Blaise Pascal. It contains many mathematical patterns that have various applications. Some key patterns discussed include the Fibonacci sequence, golden ratio, spirals, and the Sierpinski triangle. The document also explores how Pascal's triangle relates to powers of numbers, binomial coefficients, and the "hockey stick" pattern.