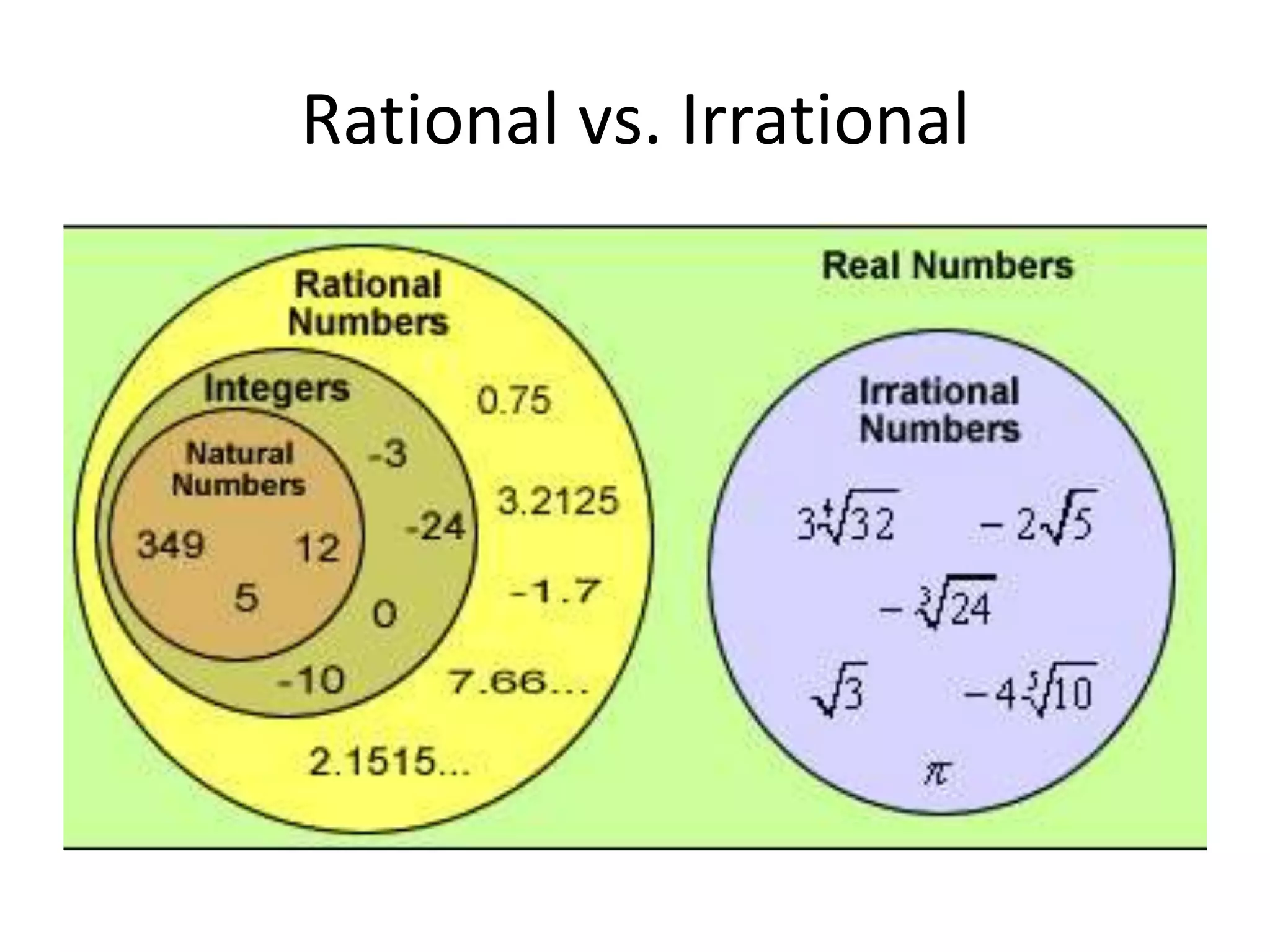
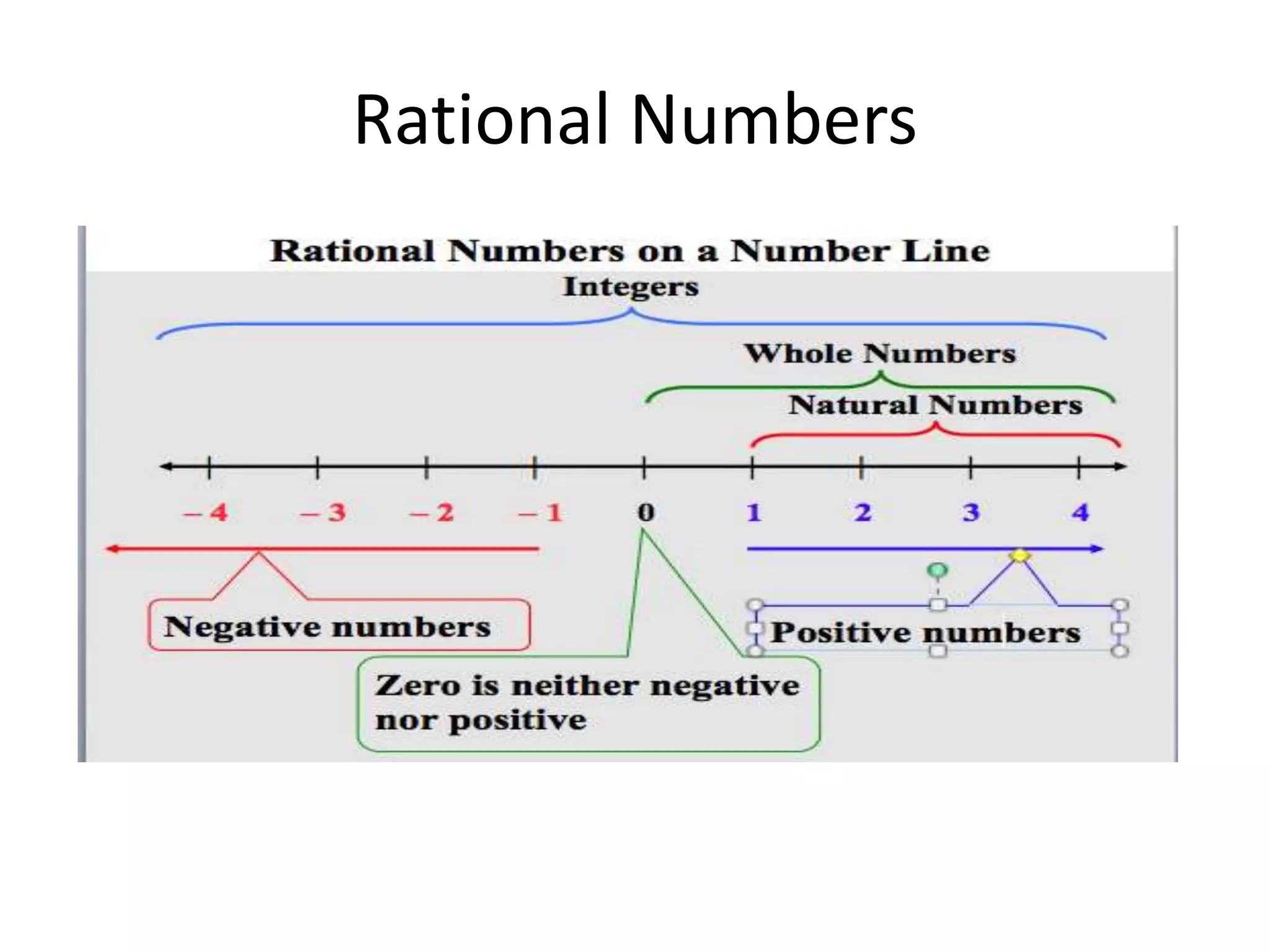
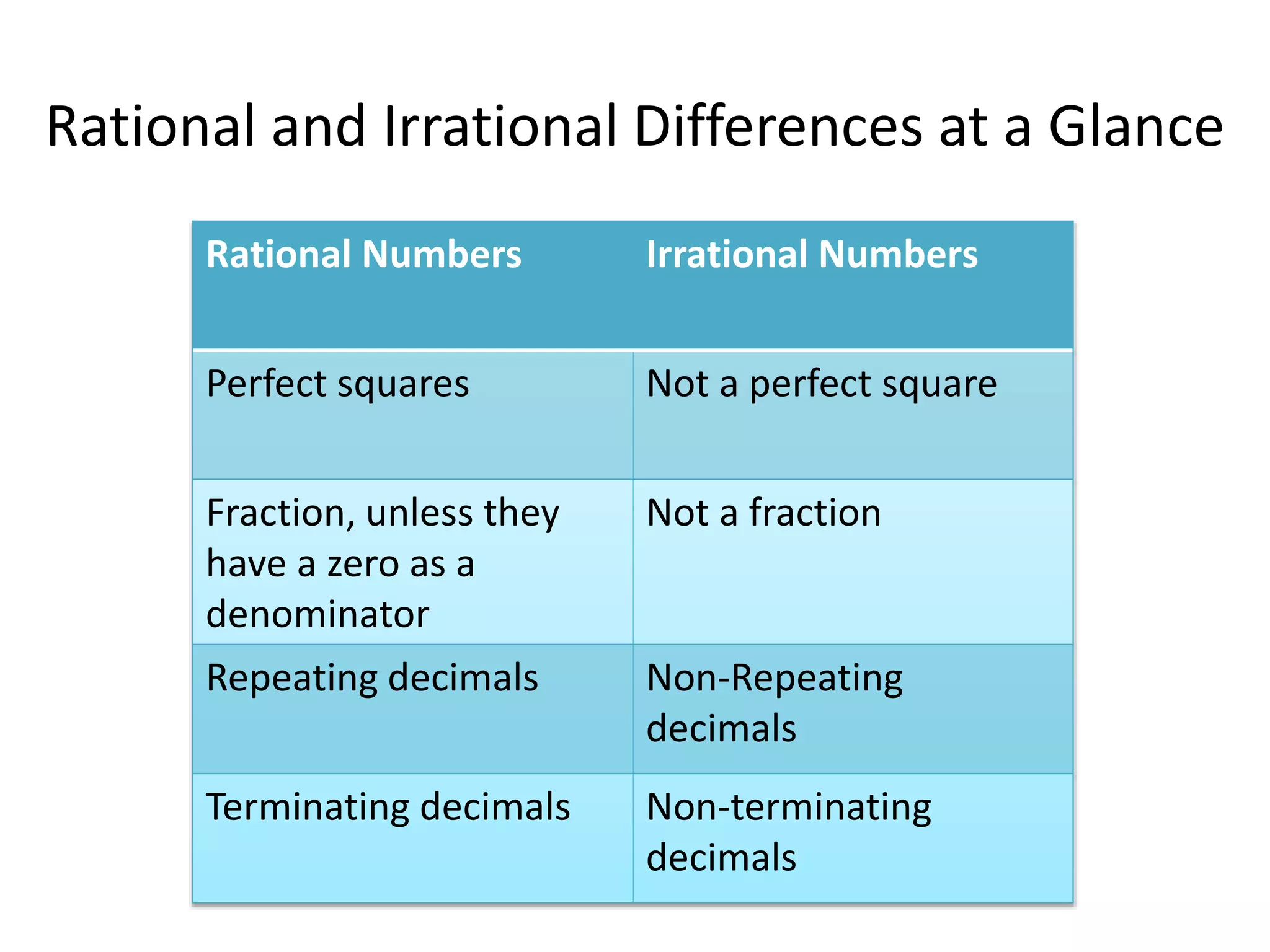
This document discusses rational and irrational numbers. Rational numbers can be written as fractions or repeating decimals, and include integers and perfect squares. Irrational numbers cannot be written as fractions and their decimals do not repeat, such as the square root of 2 or pi. Some key irrational numbers are discussed, which when calculated on a calculator either provide a non-terminating decimal or cause an error message. Rational numbers can be identified by determining if a number can be expressed as a ratio or fraction.

1. Unit 1
The Number System
8.NS
Know that there are numbers that
are not rational, and approximate
them by rational numbers.

2. MGSE8.NS.1. Know that numbers that are not
rational are called irrational. Understand informally
that every number has a decimal expansion; for
rational numbers show that the decimal expansion
repeats eventually, and convert a decimal expansion
which repeats eventually into a rational number.

3. Unit 1
The Number System
MGSE8.NS.2 Use rational approximation of irrational
numbers to compare the size of irrational numbers,
locate them approximately on a number line, and
estimate the value of expressions (e.g., estimate π2to
the nearest tenth). For example, by truncating the
decimal expansion of √2 (square root of 2), show that
√2 is between 1 and 2, then between 1.4 and 1.5, and
explain how to continue on to get better
approximations.

4. Part 1 Rational and Irrational numbers
In the world of math, Numbers can be labeled in two
different categories
Rational: Any integer (positive or negative number) that can be
written as a fraction/ratio
and
Irrational: Any integer (positive or negative number) that
cannot be written as a fraction

5. Rational vs. Irrational

6. Rational Numbers

7. Rational numbers
Look at the word RATIONAL. What word do you
see in this term?
What does this world mean?

8. Rational numbers
The term “RATIO” refers to making a comparison of two different numbers
Such as 13 girls to 15 Boys or 13:15
You may remember that we can write a ratio in three ways:
13 to 15 13:15 13/15
Because we are able to write ratios in the form
of a fraction. We can identify these numbers as
rational.

9. Rational numbers
What about whole numbers??
Why are they considered rational?
Turn to your neighbor and discuss why 3 is
considered a rational number

10. Rational numbers
Remember that all whole numbers can be
written as a fraction, just by putting a 1
underneath it. Therefore 3 can be written as a
fraction and is considered rational.

11. Decimals and rational numbers
If decimal form is another way to write a fraction, does
this mean every decimal number is a fraction?
This is where it can get confusing!

12. Decimals and rational numbers
Rational numbers that are expressed
as a ration that
REPEAT
Or
TERMINATE

13. Terminating Decimal
Think about the word
terminate…What does it mean?
Notice that these decimals end on their
own, these numbers were not rounded.
They Terminated.
Terminating numbers are RATIONAL

14. Terminating Decimal
Terminating numbers can be written
as a fraction
5/10 or ½
75/100 or ¾
287/1000
89/100

15. Repeating numbers
Using a calculator, you can use your phone for
this!, Calculate 1 divided by 3.
What did you get?

16. Repeating Decimals
These threes will never end, they will repeat forever.
To represent the repetition in a decimal, we can put a line
over the first time the repeating numbers are shown and
drop all the other numbers behind ig

17. Repeating Decimals
These threes will never end, they will repeat forever.
To represent the repetition in a decimal, we can put a line
over the first time the repeating numbers are shown and
drop all the other numbers behind it.

18. Repeating Decimals
The process of dropping numbers without rounding is called Truncating
ANY TIME YOU TRUNCATE A REPEATING DECIMAL YOU
MUST PUT A LINE ABOVE ALL OF THE NUMBERS.
F.Y.I.
THIS LINE IS
CALLED A
VINCLULUM

19. Repeating Decimals
Truncate and place the vinculum in
its appropriate place.

20. Repeating Decimals
Truncate and place the vinculum in
its appropriate place.
ALL REPEATING NUMBERS CAN BE TRUNCATED AND
WRITTEN AS A FRACTION. THEREFORE, REPEATING
NUMBERS ARE RATIONAL

21. Perfect Squares, numbers that
are the product of a number multiplied
by itself, are also rational

22. IRRATIONAL NUMBERS
Have you ever heard someone say
“you are being irrational”?
What do you think that means?

23. IRRATIONAL NUMBERS
QUICKLY TURN TO YOUR NEIGBOR AND TALK ABOUT WHY
THIS IMAGE IS IRRATIONAL?

24. IRRATIONAL NUMBERS
The term IRRATIONAL is defined as something that is
illogical or unreasonable. In other other words,
IT DOESN’T MAKE SENSE.

25. IRRATIONAL NUMBERS
Let’s think about
NEVER ENDS, IT GOES ON FOREVER

26. IRRATIONAL NUMBERS
Let’s think about
ALSO NEVER REPEATS.

27. IRRATIONAL NUMBERS
IF NEVER REPEATS
IF NEVER ENDS
&
HOW CAN WE WRITE AS A FRACTION?

28. IRRATIONAL NUMBERS
Because we cannot write as a fraction, we call it Irrational
Other numbers include the following
Go ahead and put these in your calculator and see what you
get.

29. IRRATIONAL NUMBERS
You make get a long answer, or even an error message.
This indicates that the number is irrational.

30. Rational and Irrational Differences at a Glance
Rational Numbers Irrational Numbers
Perfect squares Not a perfect square
Fraction, unless they
have a zero as a
denominator
Not a fraction
Repeating decimals Non-Repeating
decimals
Terminating decimals Non-terminating
decimals