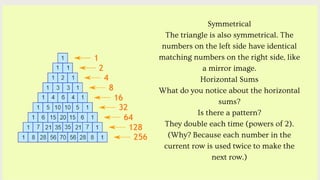
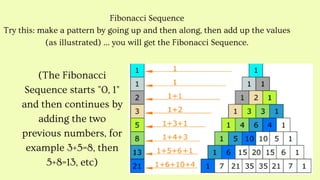
Pascal's Triangle is a triangular array of numbers that represents coefficients in binomial expansions, revealing interesting patterns and properties. Each row starts with 1, and other numbers are derived from the sum of the two numbers directly above them, showcasing symmetrical properties and relationships to powers of 2, Fibonacci sequence, and binomial coefficients. The document also discusses the significance of these patterns in various mathematical fields such as probability and combinatorics.

1. Understanding
Pascal's Triangle
Exploring its Patterns and Properties

2. Exploring the Fascinating Pascal's
Triangle
Pascal's triangle reveals patterns in binomial coefficients.
Pascal's triangle, in algebra, a triangular arrangement
of numbers that gives the coefficients in the
expansion of any binomial expression, such as (x + y)n.
It is named for the 17th-century French
mathematician Blaise Pascal, but it is far older.

3. Exploring Pascal's
Triangle Basics A pascal's triangle is an
arrangement of numbers in a
triangular array such that the
numbers at the end of each row are
1 and the remaining numbers are
the sum of the nearest two
numbers in the above row. This
concept is used widely in
probability, combinatorics, and
algebra.

4. Exploring the Fascinating Pascal's Triangle
Understanding its patterns and mathematical significance.
To build the triangle, start with "1" at the top, then continue
placing numbers below it in a triangular pattern.
Each number is the numbers directly above it added
together.
(Here I have highlighted that 1+3 = 4)

5. Patterns Within the Triangle
Diagonals
The first diagonal is, of course, just
"1"s
The next diagonal has the Counting
Numbers (1,2,3, etc).
The third diagonal has the
triangular numbers
(The fourth diagonal, not
highlighted, has the tetrahedral
numbers.)

6. Symmetrical
The triangle is also symmetrical. The
numbers on the left side have identical
matching numbers on the right side, like
a mirror image.
Horizontal Sums
What do you notice about the horizontal
sums?
Is there a pattern?
They double each time (powers of 2).
(Why? Because each number in the
current row is used twice to make the
next row.)

7. Horizontal Sums
What do you notice about the horizontal sums?
Is there a pattern?
They double each time (powers of 2).
(Why? Because each number in the current row
is used twice to make the next row.)

8. Exponents of 11
Each line is also the powers
(exponents) of 11:
> 110=1 (the first line is just a "1")
>111=11 (the second line is "1" and
"1")
> 112=121 (the third line is "1", "2",
"1")
etc!

9. But what happens with 115 ?
Simple! The digits just
overlap, like this:

10. Odds and Evens
If we color the Odd
and Even numbers,
we end up with a
pattern the same
as the Sierpinski
Triangle

11. The same thing happens with 116 etc.
Squares
For the second diagonal, the
square of a number is equal to
the sum of the numbers next to
it and below both of those.
Examples:
32 = 3 + 6 = 9,
42 = 6 + 10 = 16,
52 = 10 + 15 = 25,
...

12. Fibonacci Sequence
Try this: make a pattern by going up and then along, then add up the values
(as illustrated) ... you will get the Fibonacci Sequence.
(The Fibonacci
Sequence starts "0, 1"
and then continues by
adding the two
previous numbers, for
example 3+5=8, then
5+8=13, etc)

13. BINOMIAL THEOREM

14. The binomial theorem formula is
(a+b)n= ∑nr=0nCr an-rbr, where
n is a positive integer and a, b are
real numbers, and 0 < r ≤ n. This
formula helps to expand the
binomial expressions such as (x +
a)10, (2x + 5)3, (x - (1/x))4,
and so on.
What is binomial
theorem

15. What is a binomial
coefficient with an
example?
In combinatorics, the binomial coefficient is used to denote the
number of possible ways to choose a subset of objects of a
given numerosity from a larger set. It is so called because it
can be used to write the coefficients of the expansion of a
power of a binomial.

16. Binomial theorem
expansion formula
The binomial theorem formula is (a+b)n=
∑nr=0nCr an-rbr, where n is a positive
integer and a, b are real numbers, and 0 <
r ≤ n. This formula helps to expand the
binomial expressions such as (x + a)10,
(2x + 5)3, (x - (1/x))4, and so on.

17. If a and b are real numbers and n is a
positive integer, then (a + b)n =nC0 an +
nC1 an – 1 b1 + nC2 an – 2 b2 + ... 1.
The total number of terms in the binomial
expansion of (a + b)n is n + 1, i.e. one
more than the exponent n.
What is the formula for
the binomial theorem
combination?