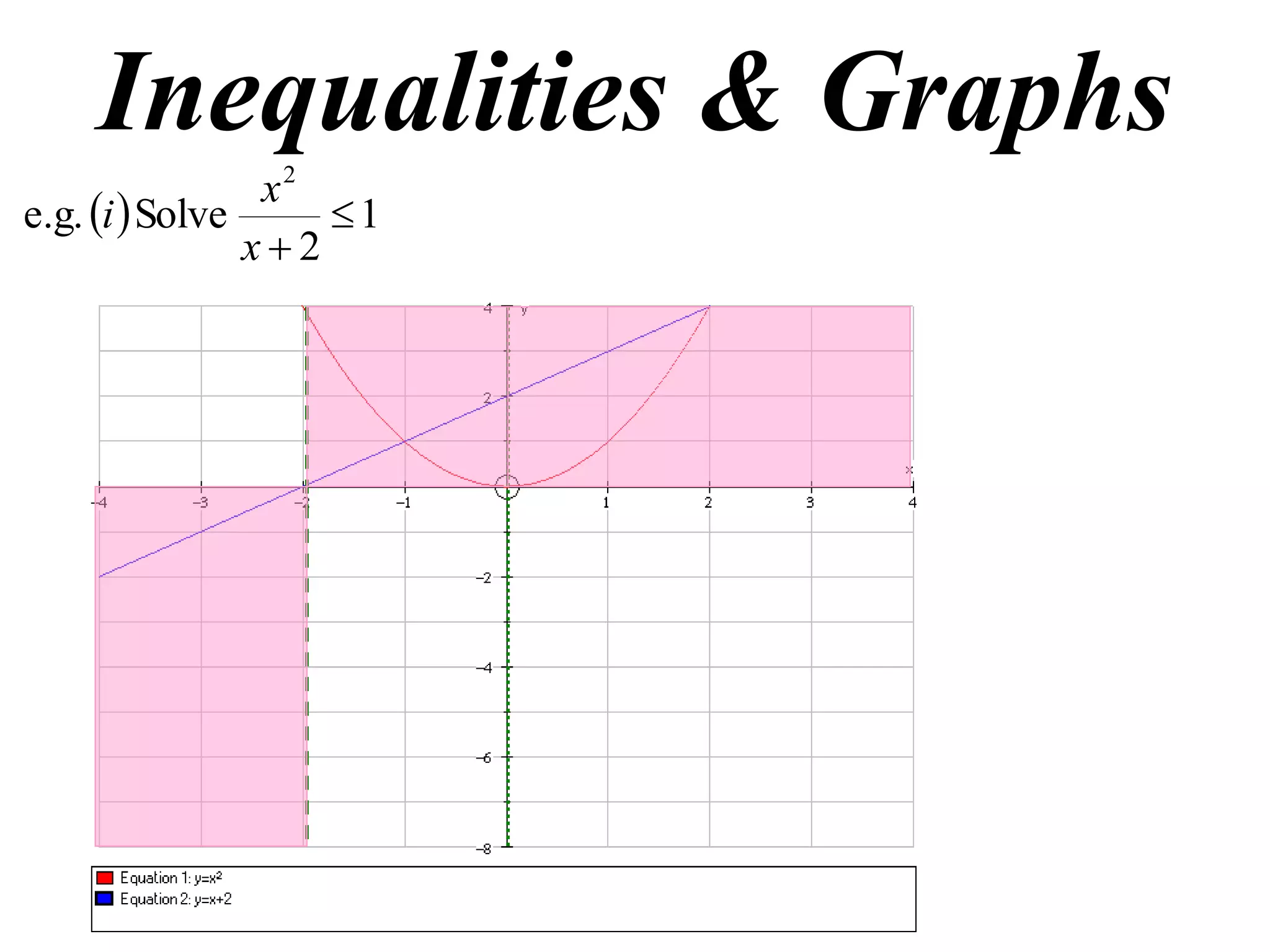
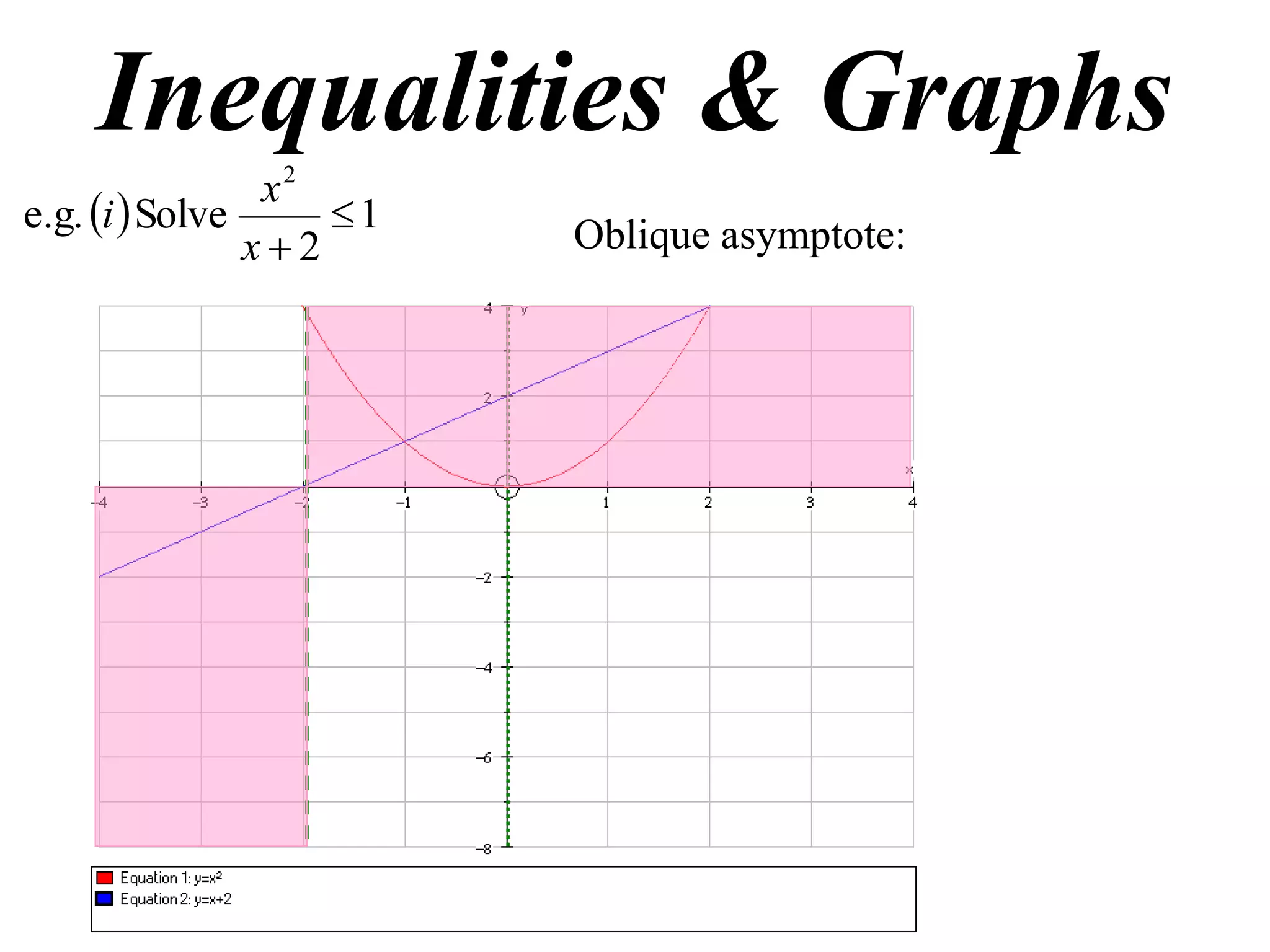
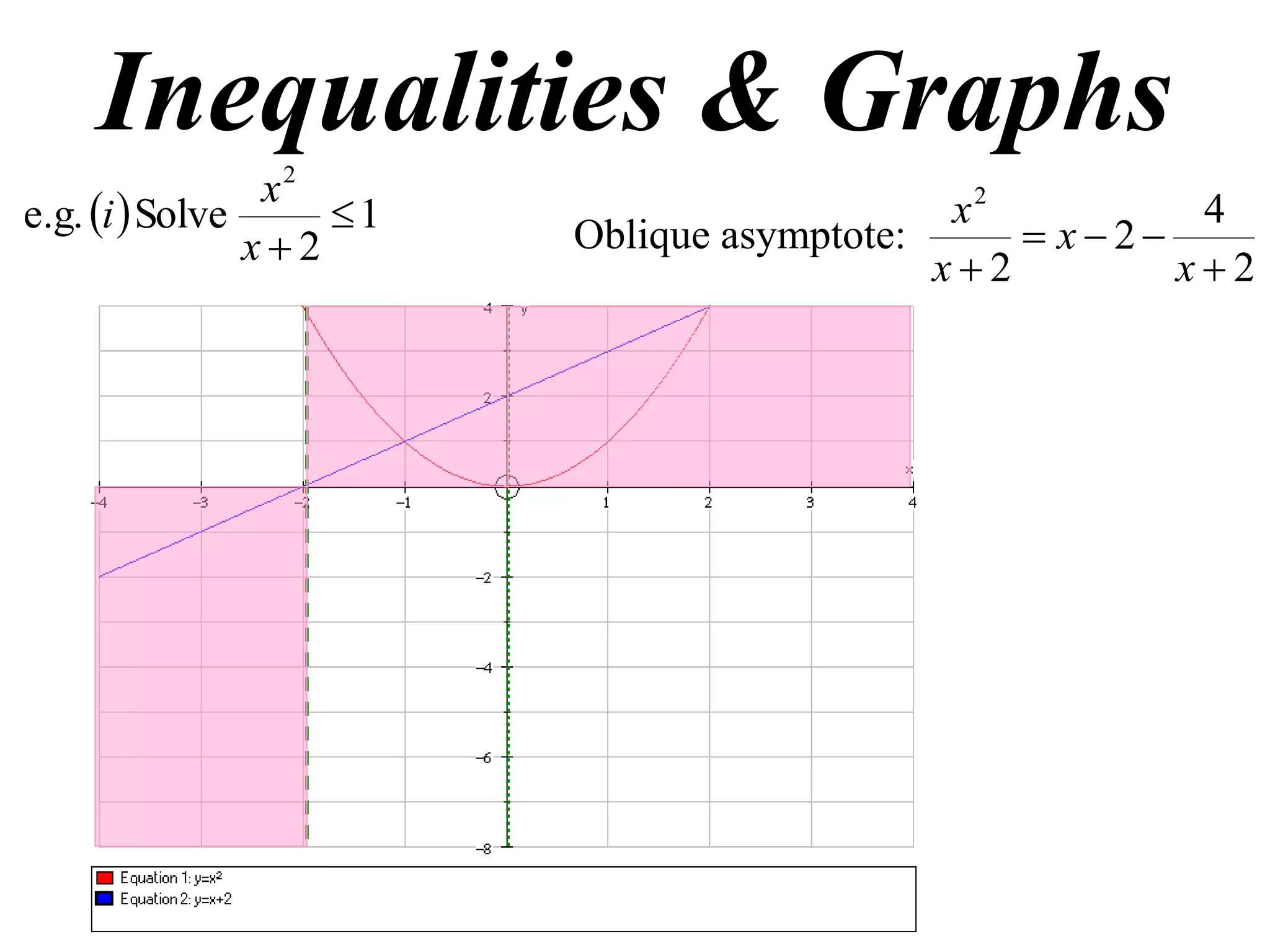
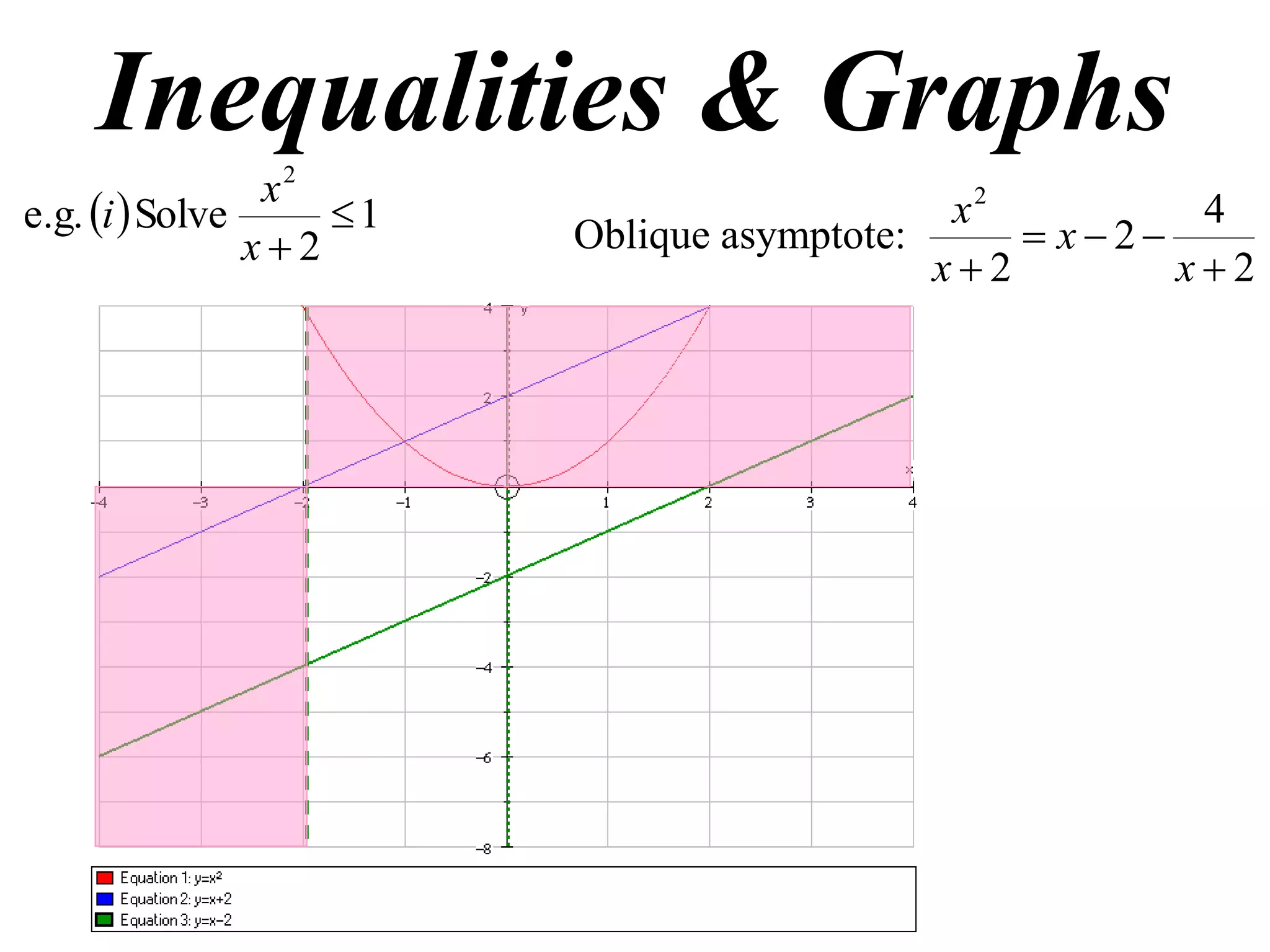
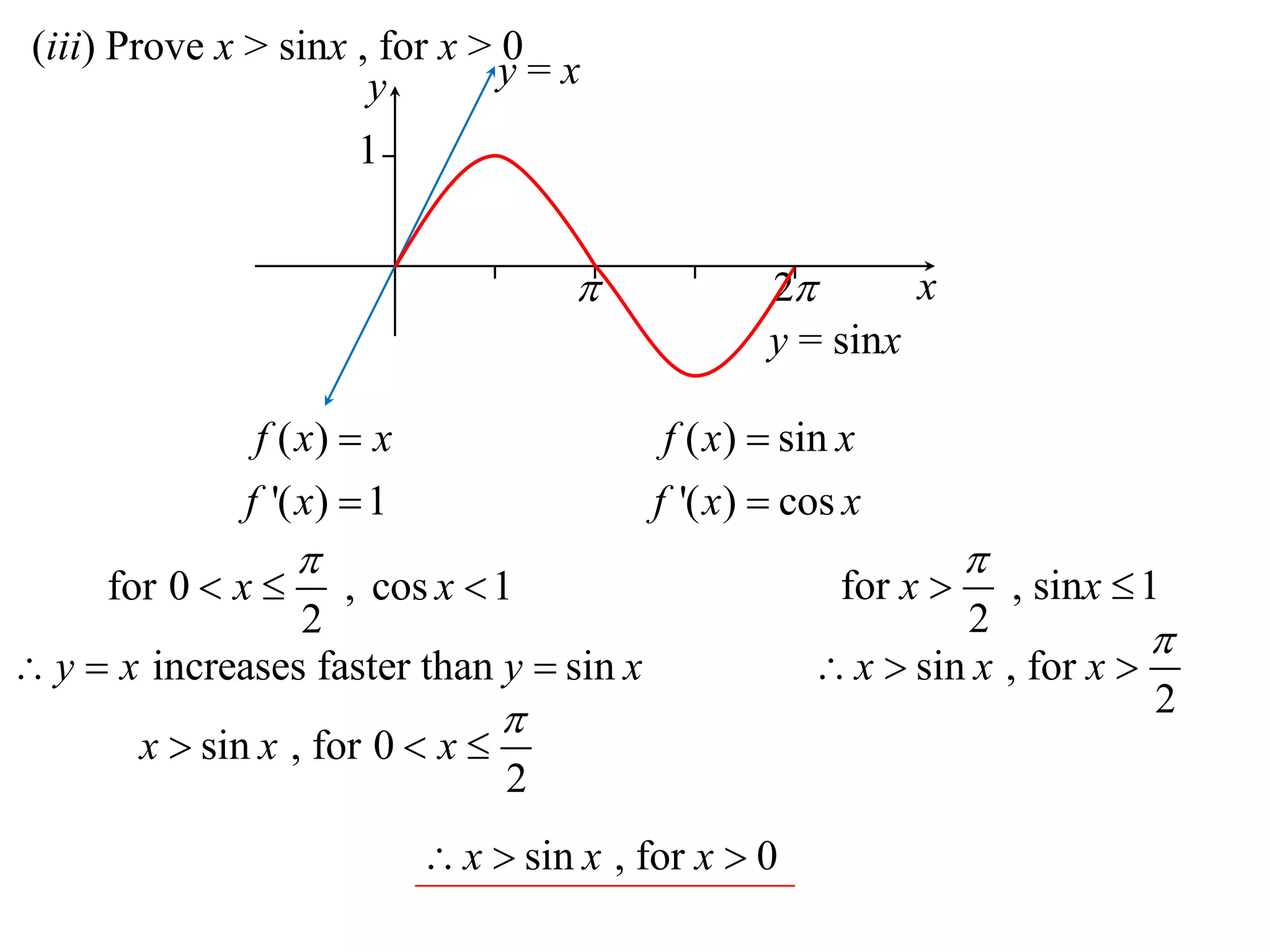
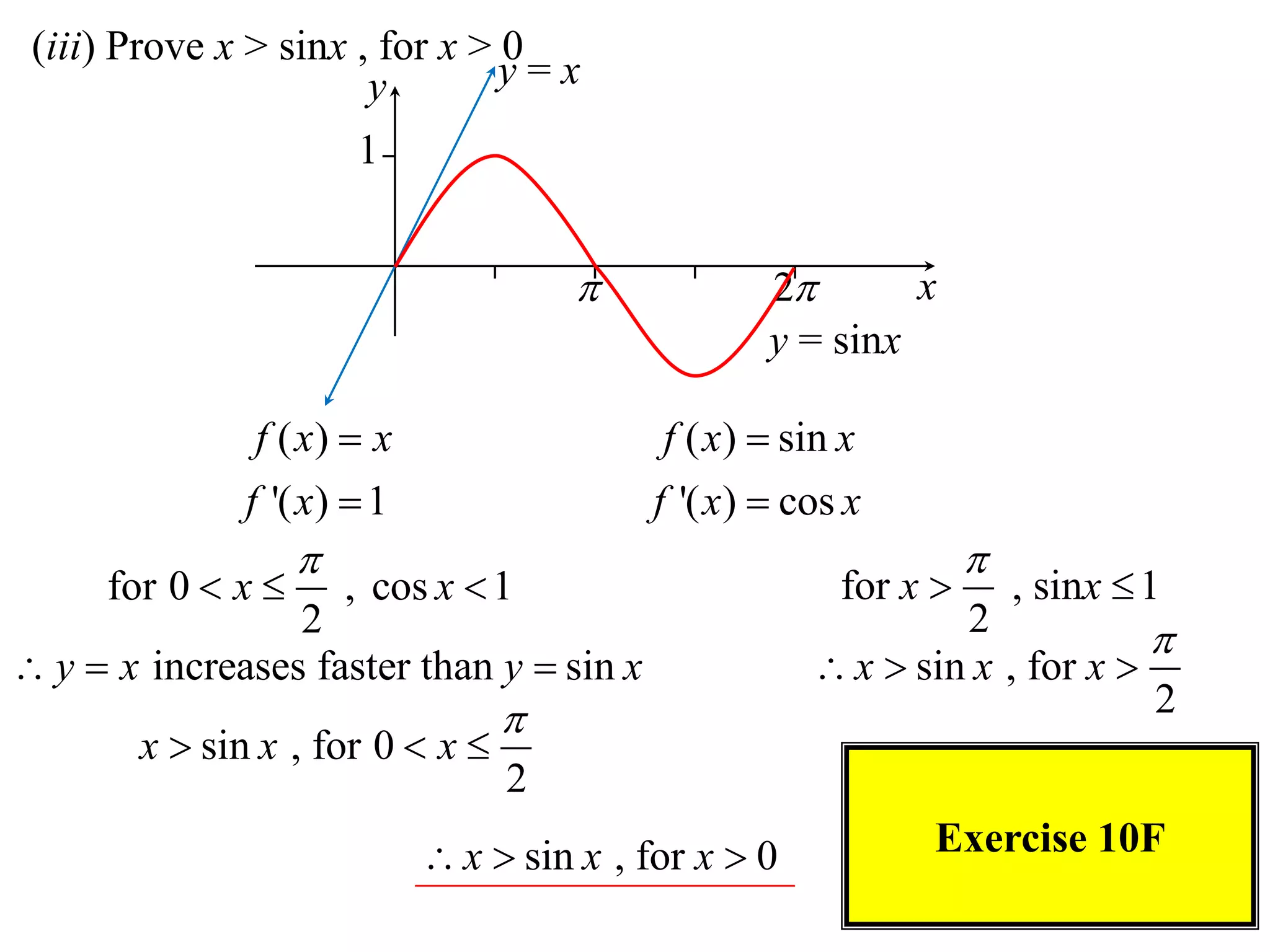
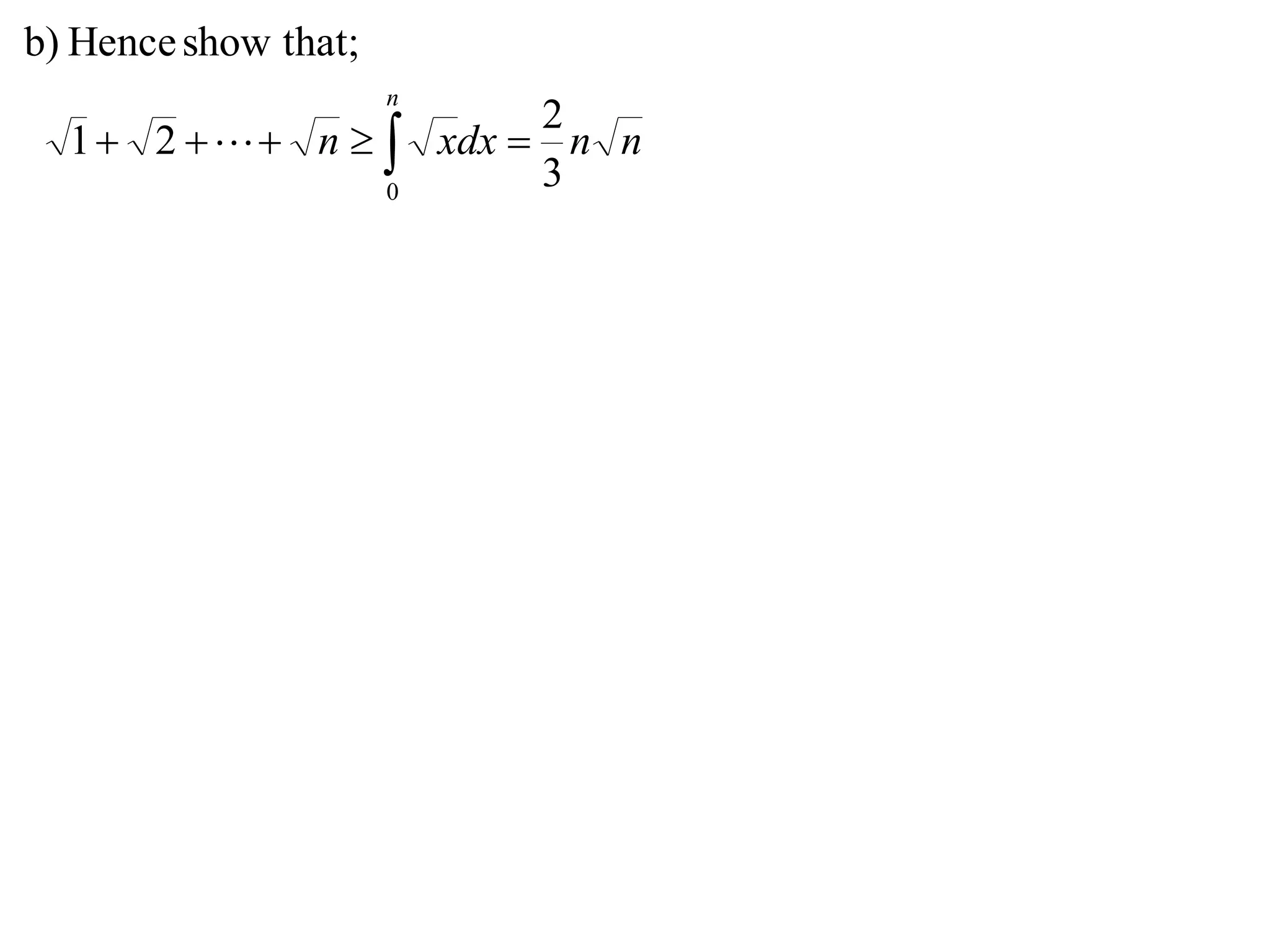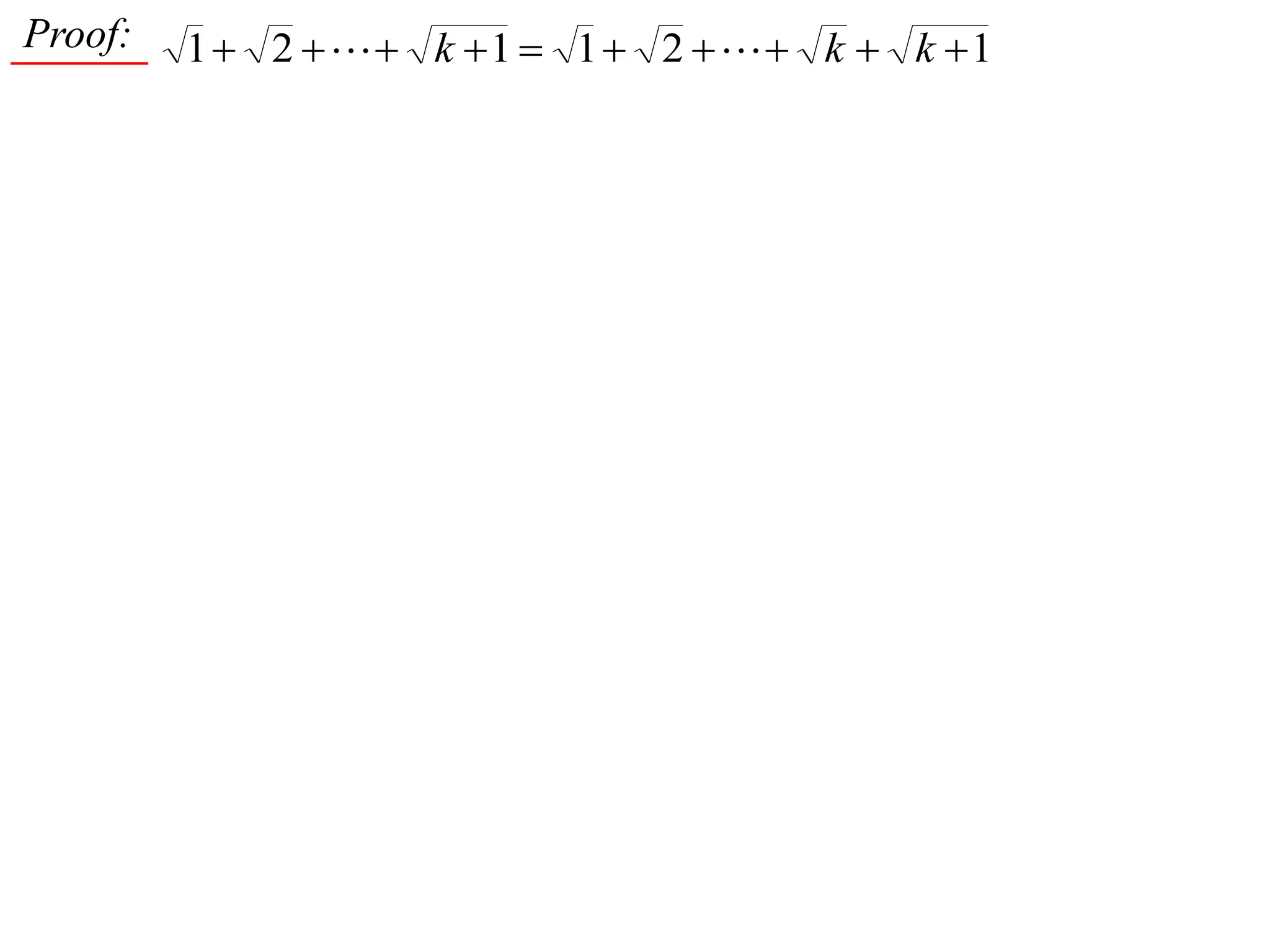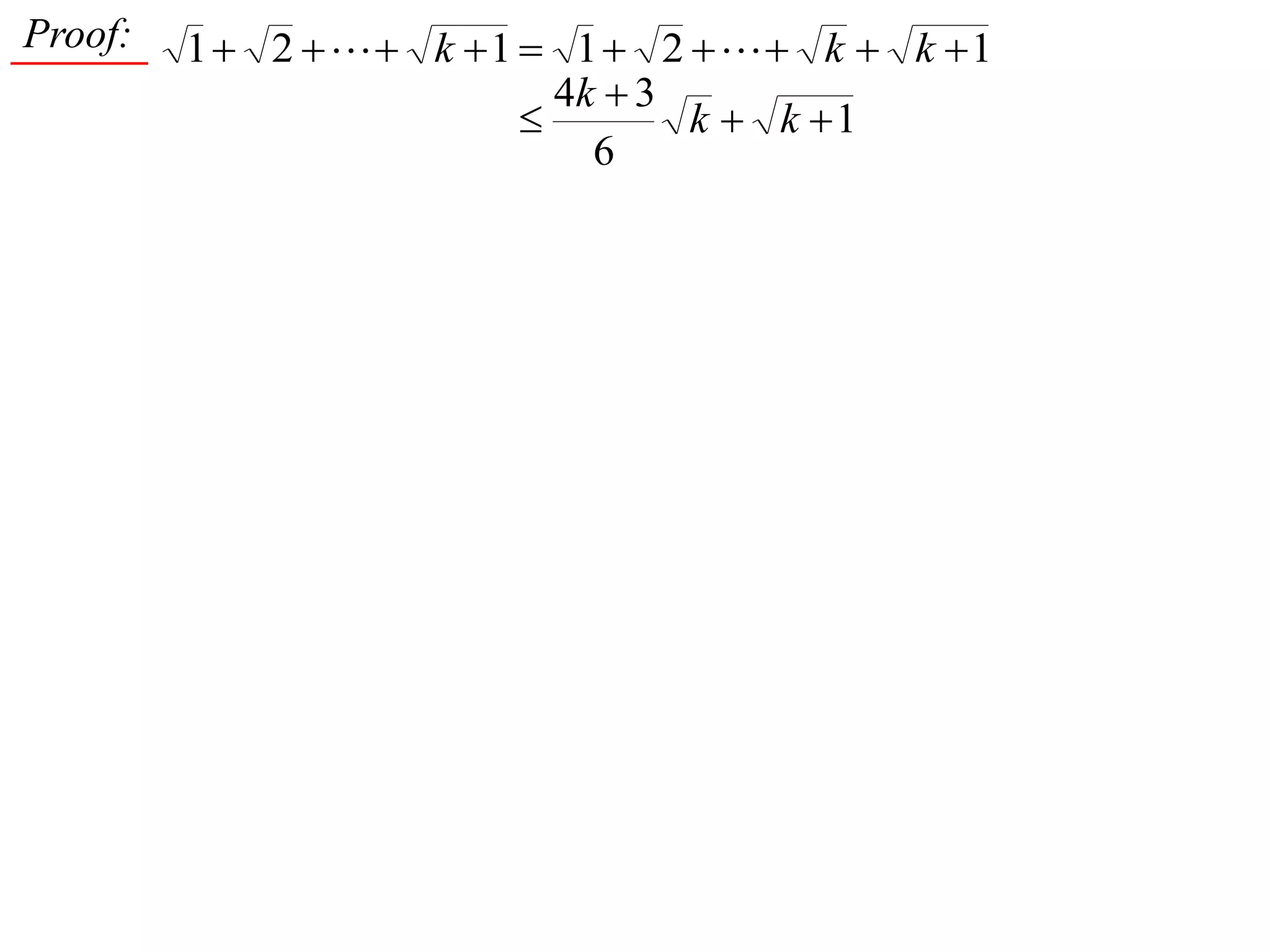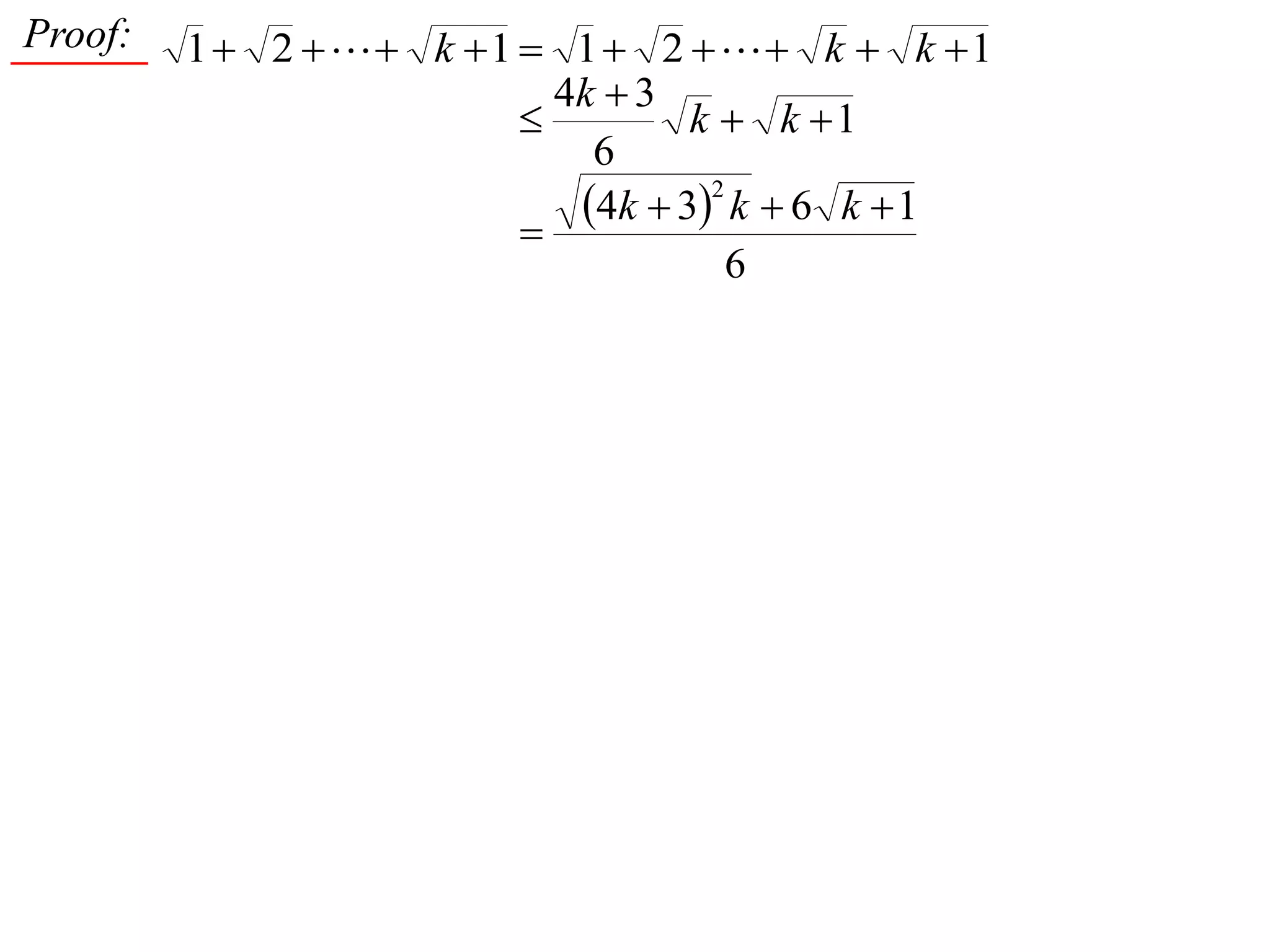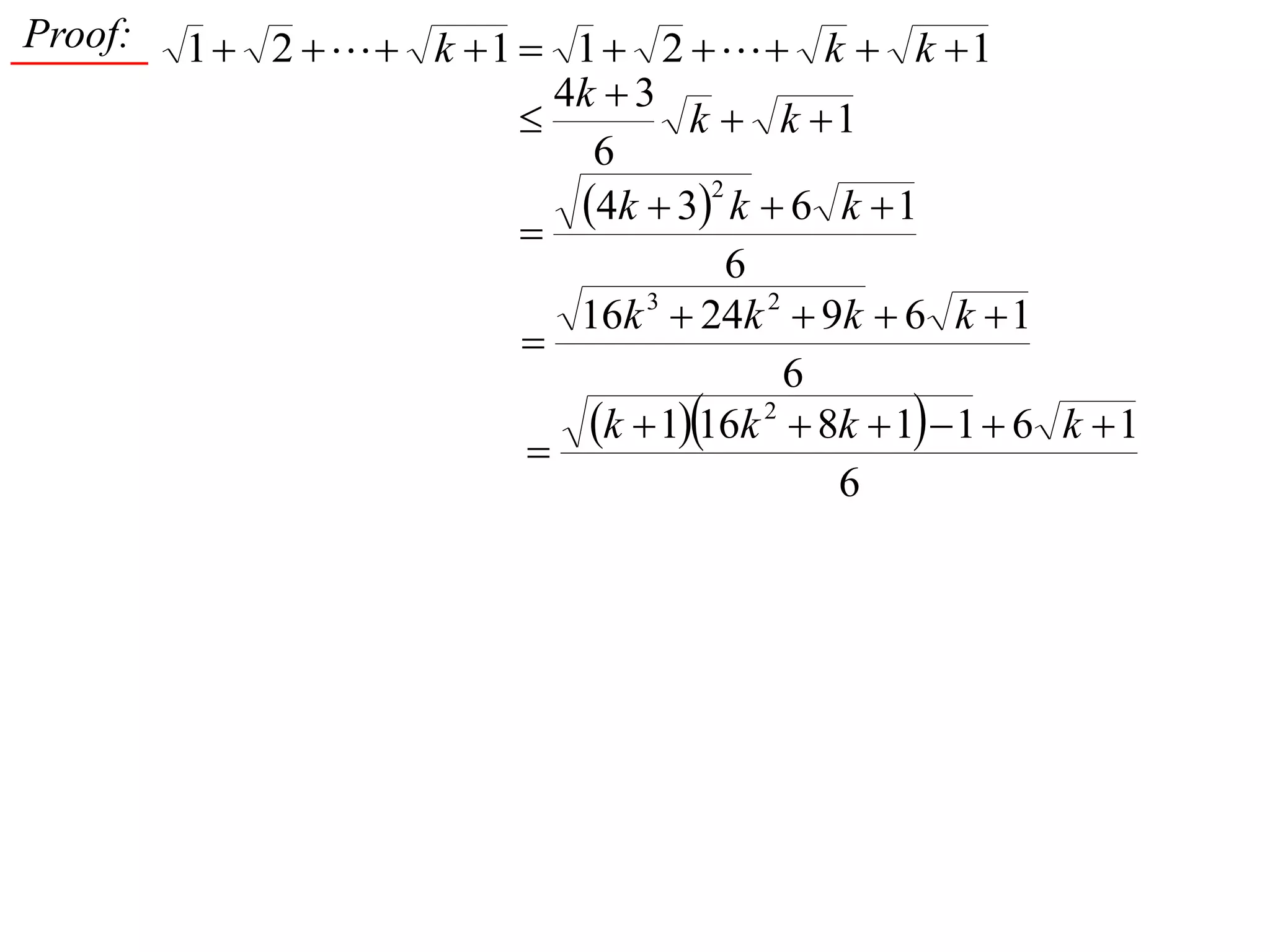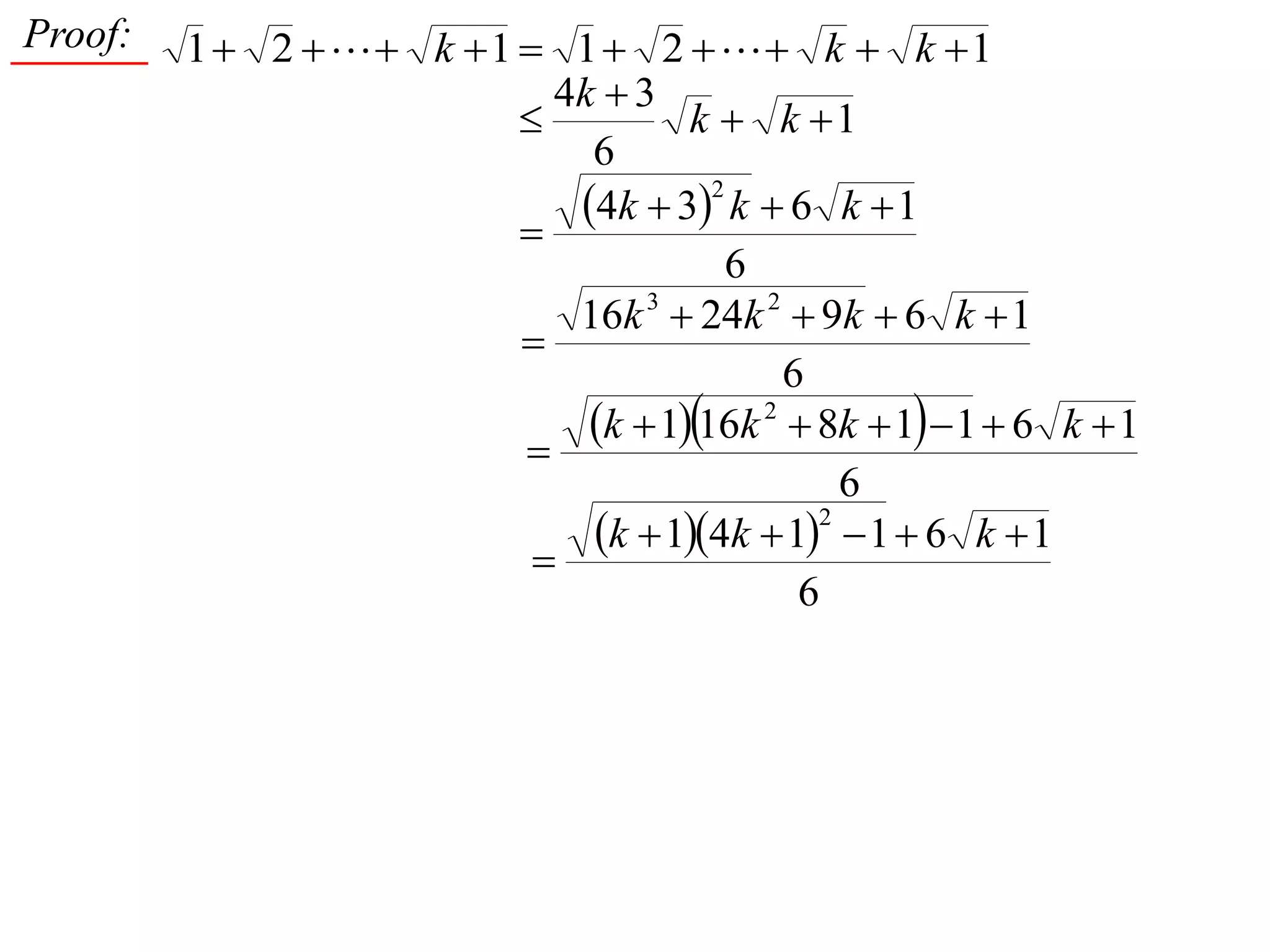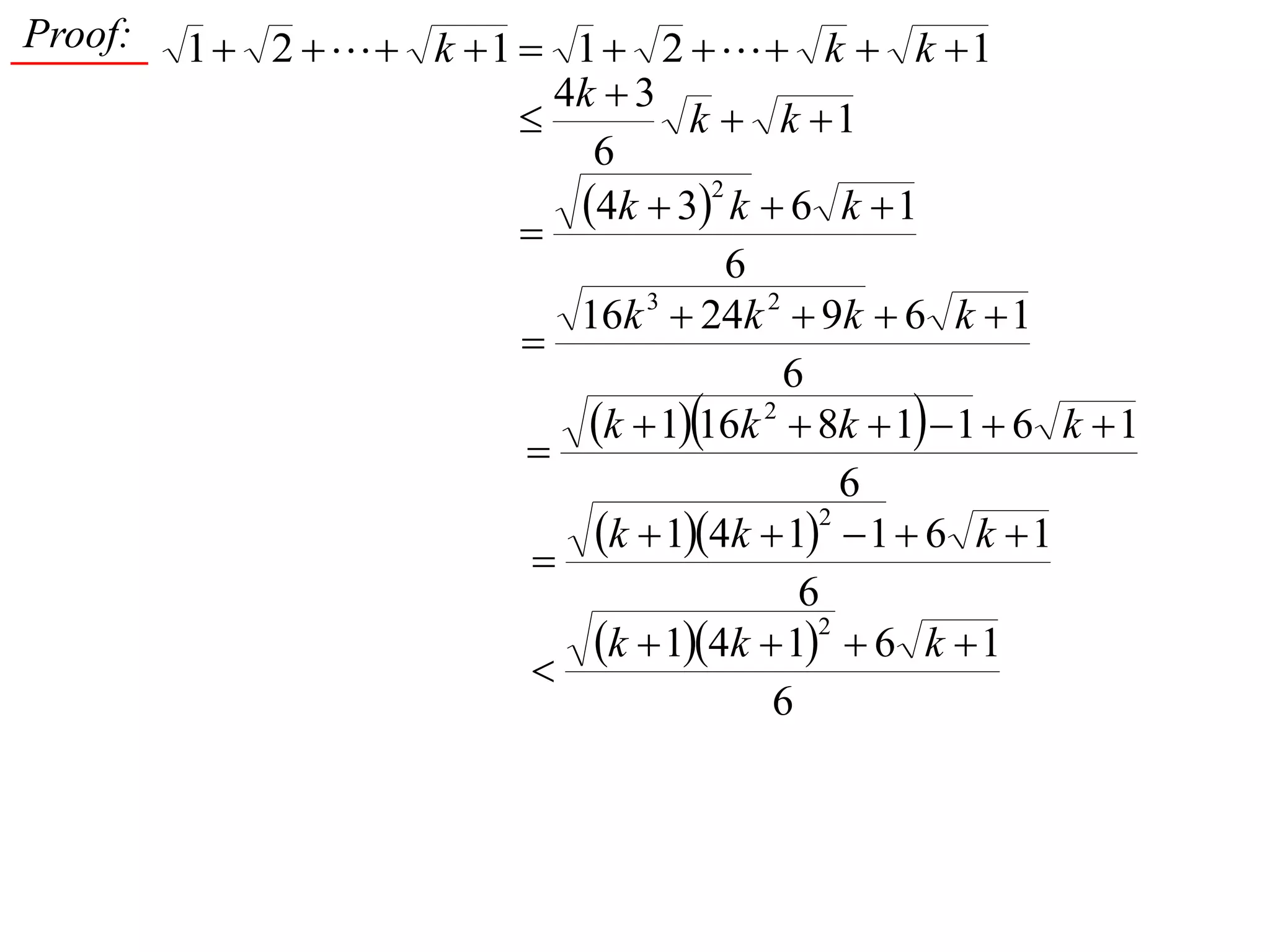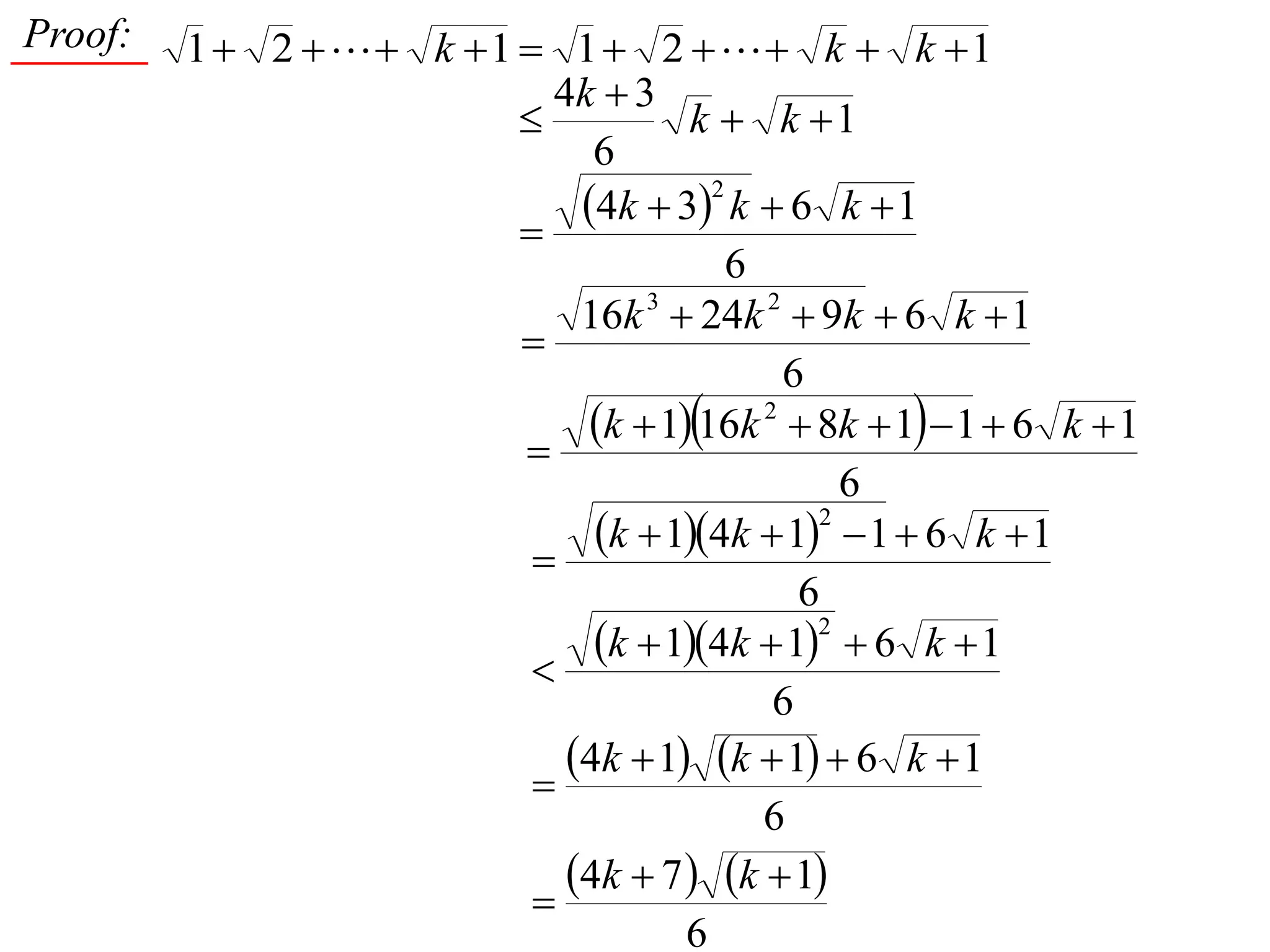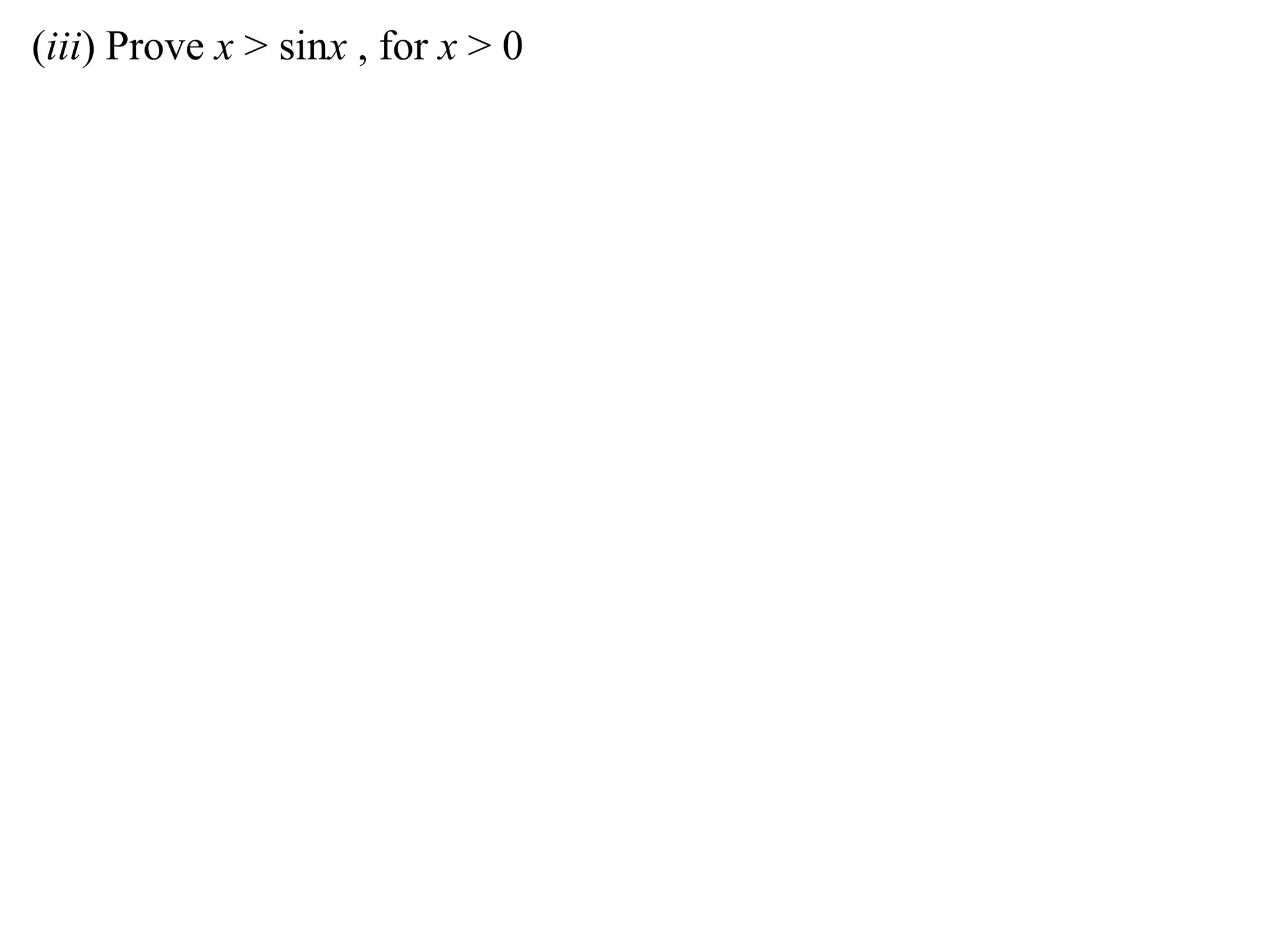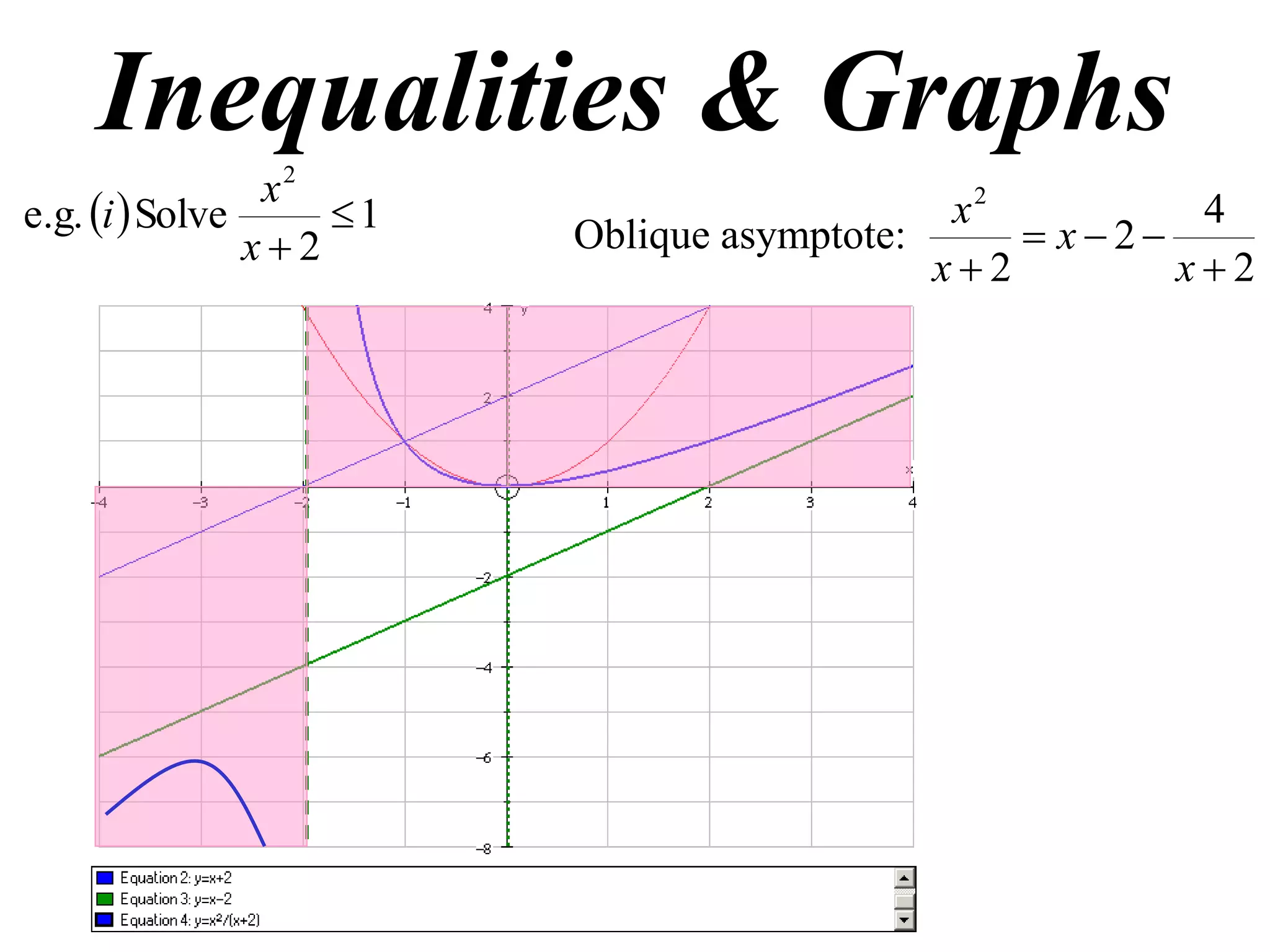
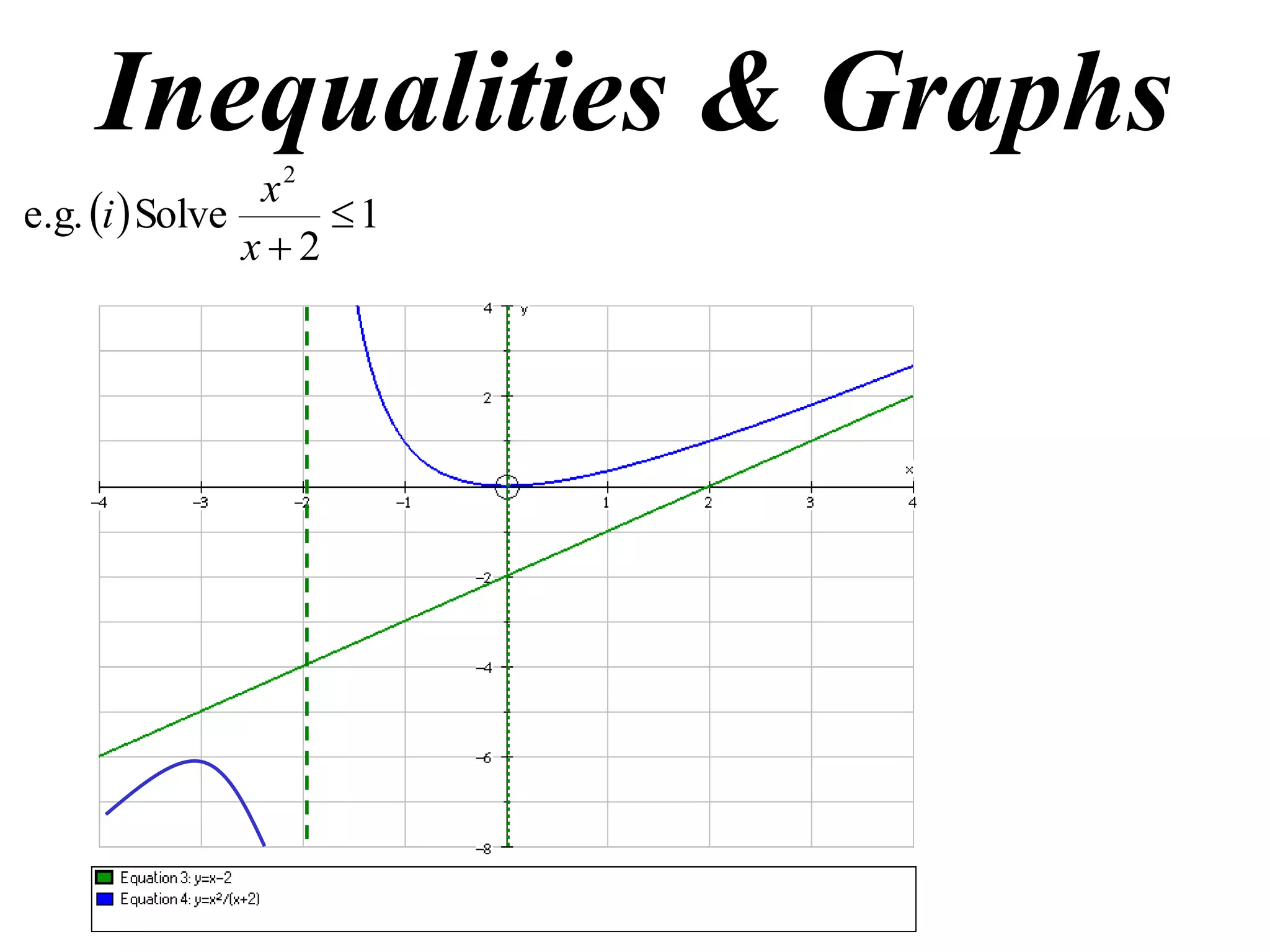
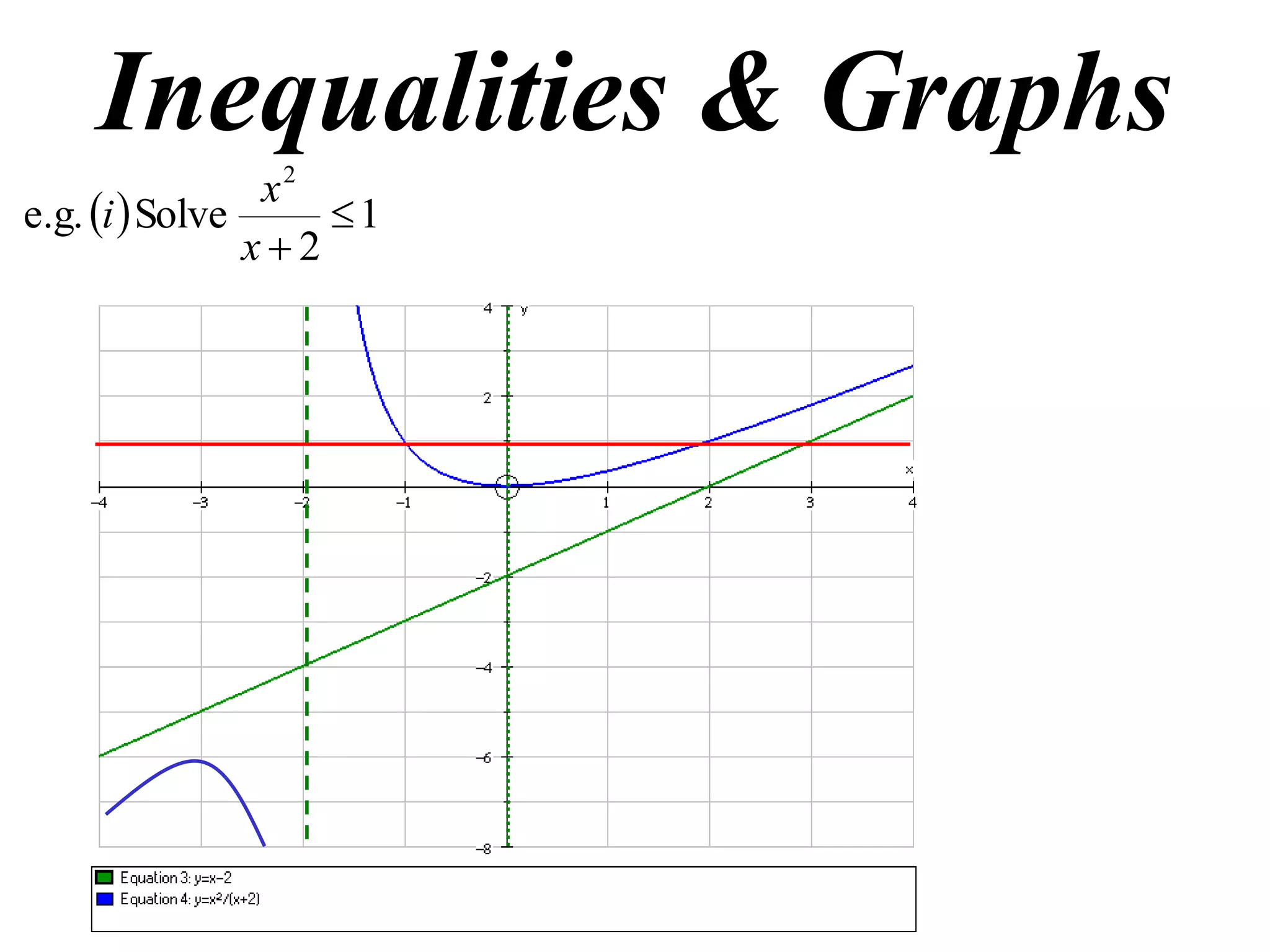
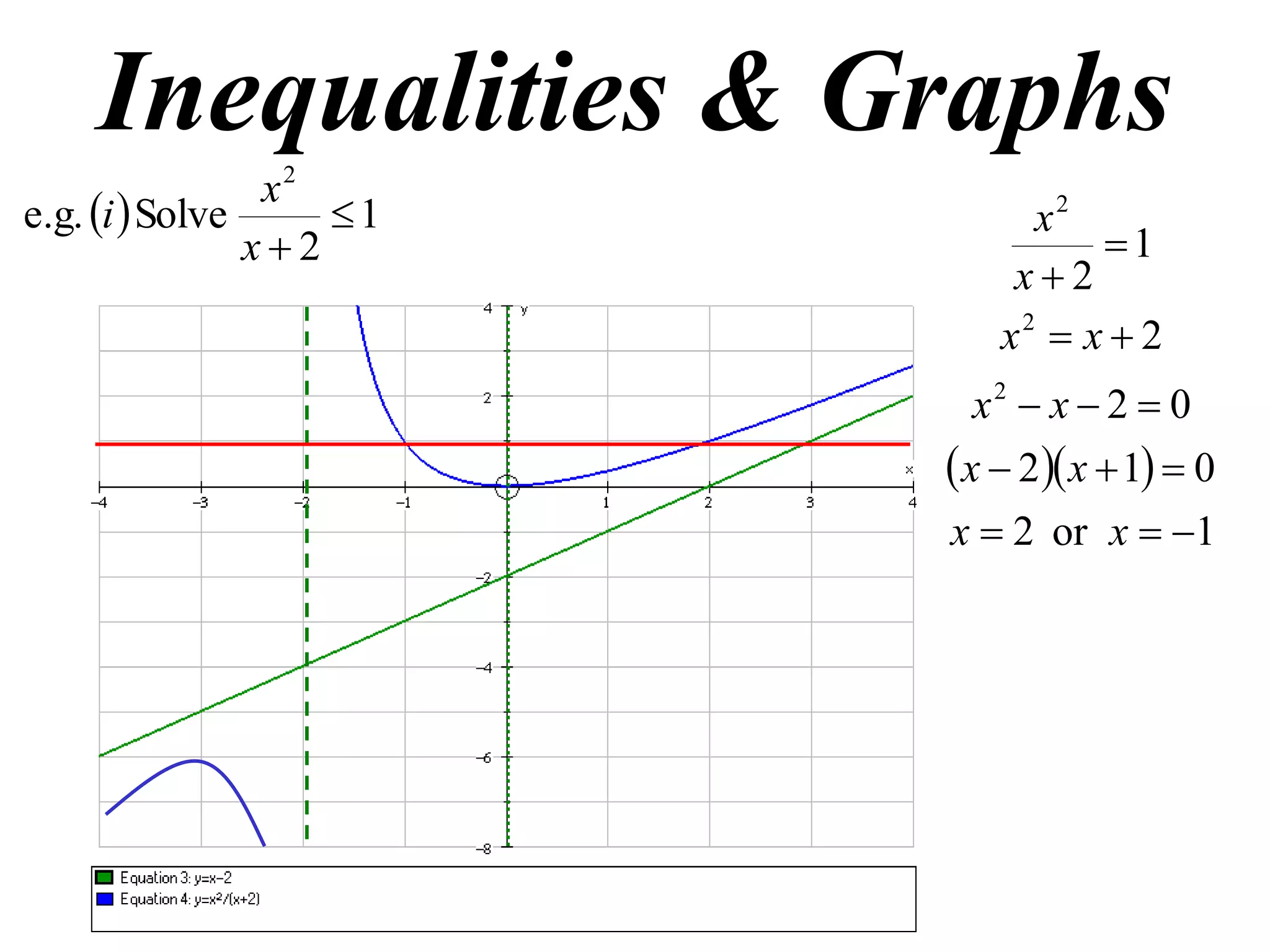
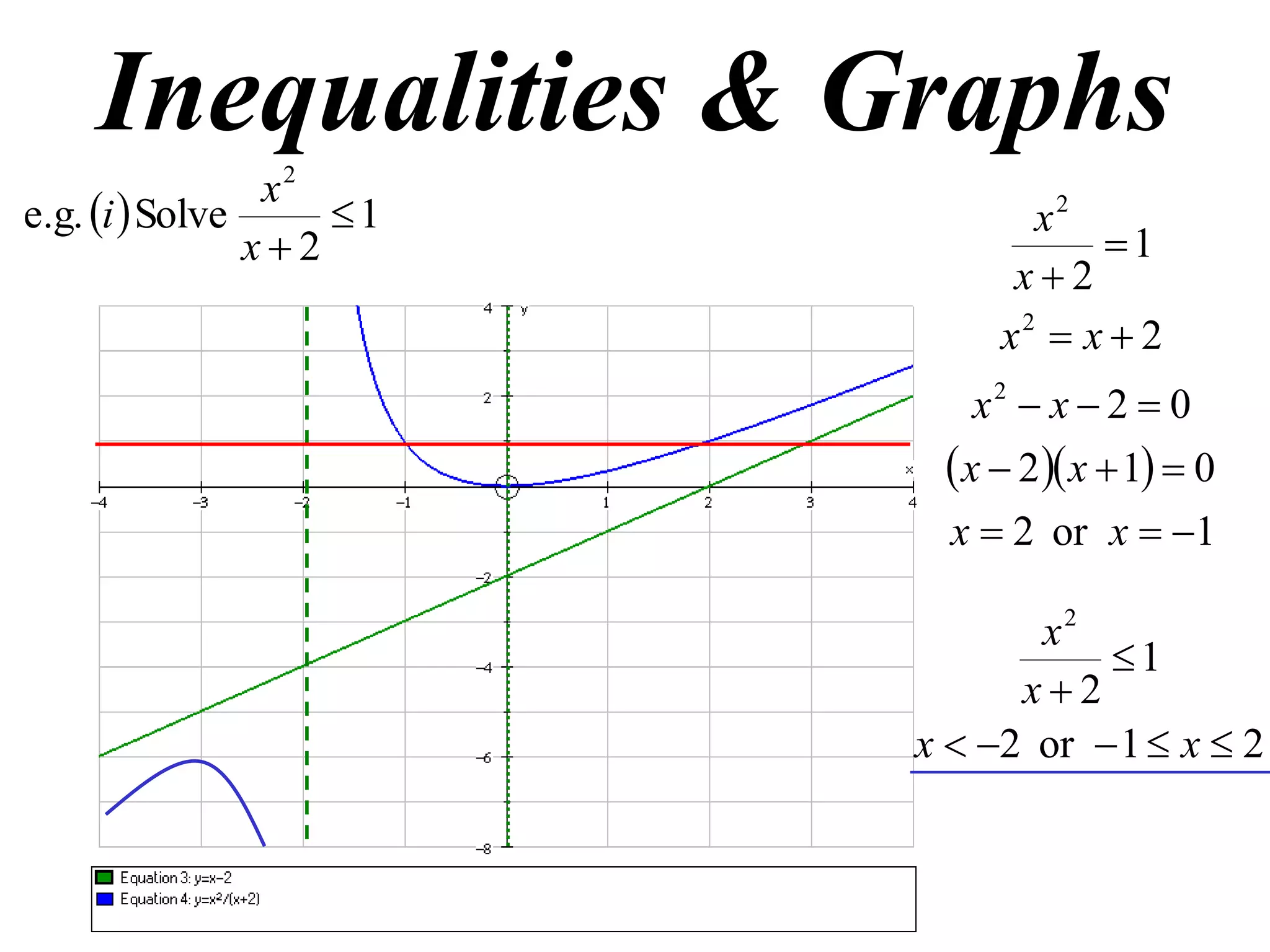
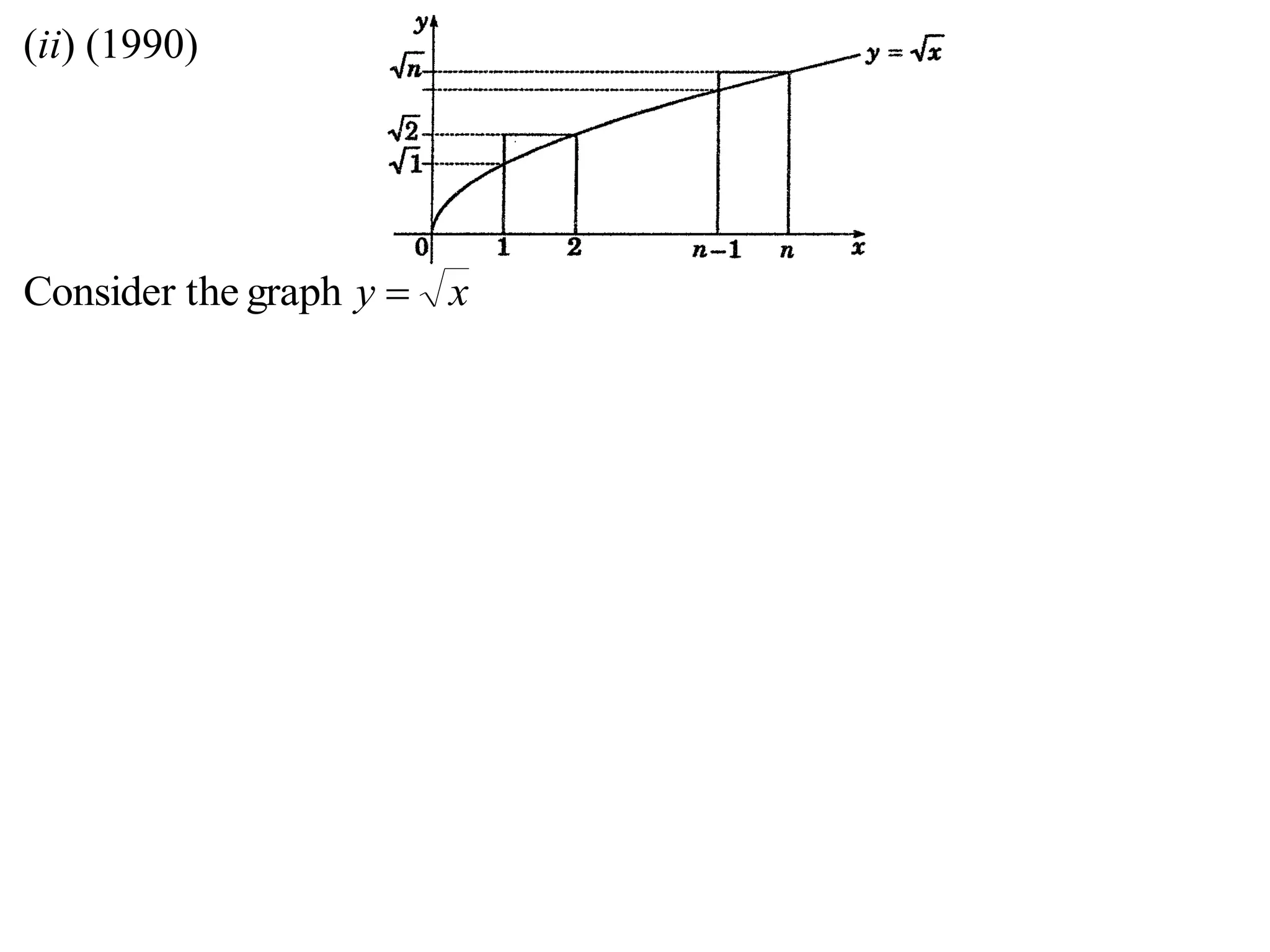
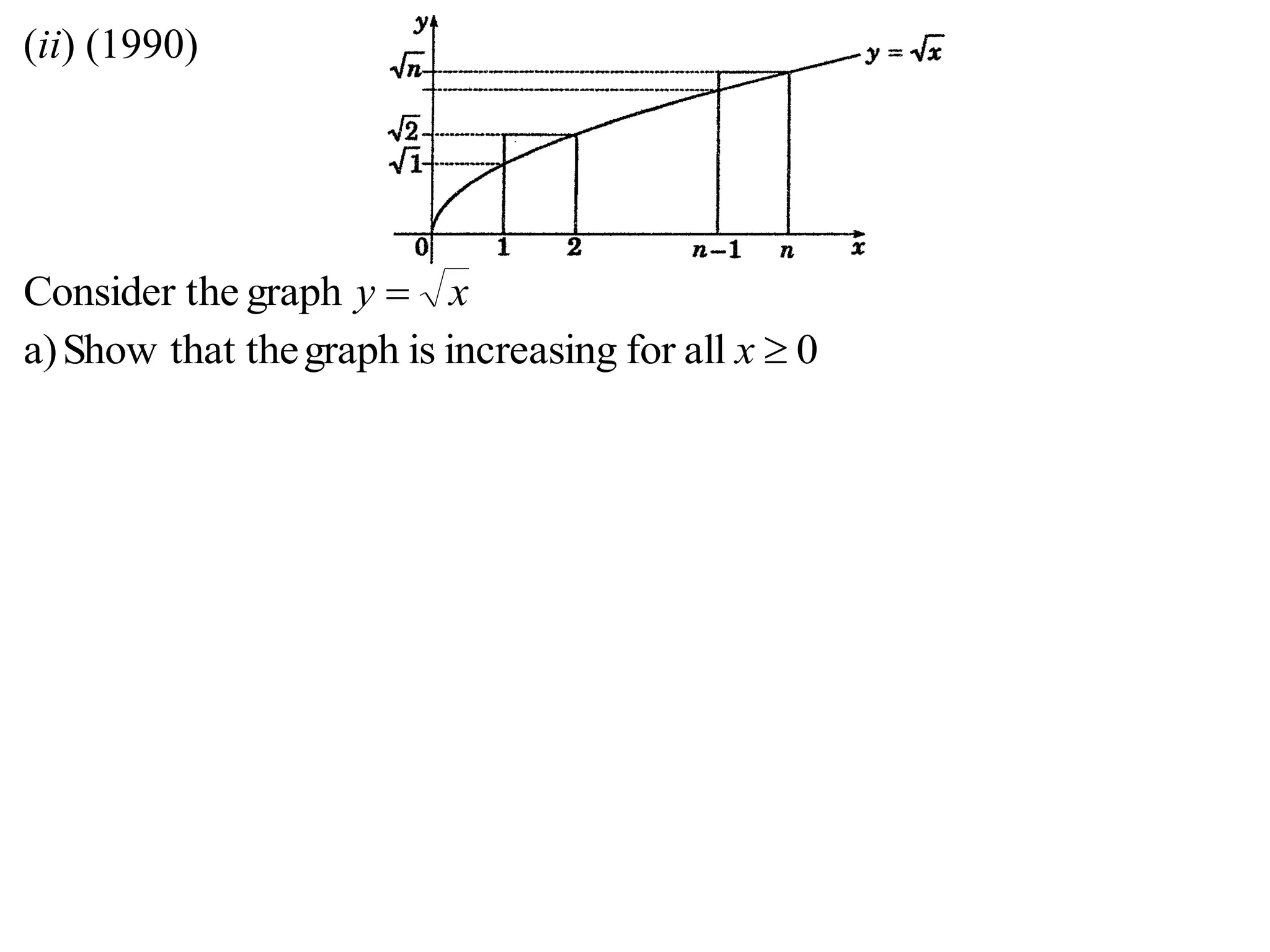
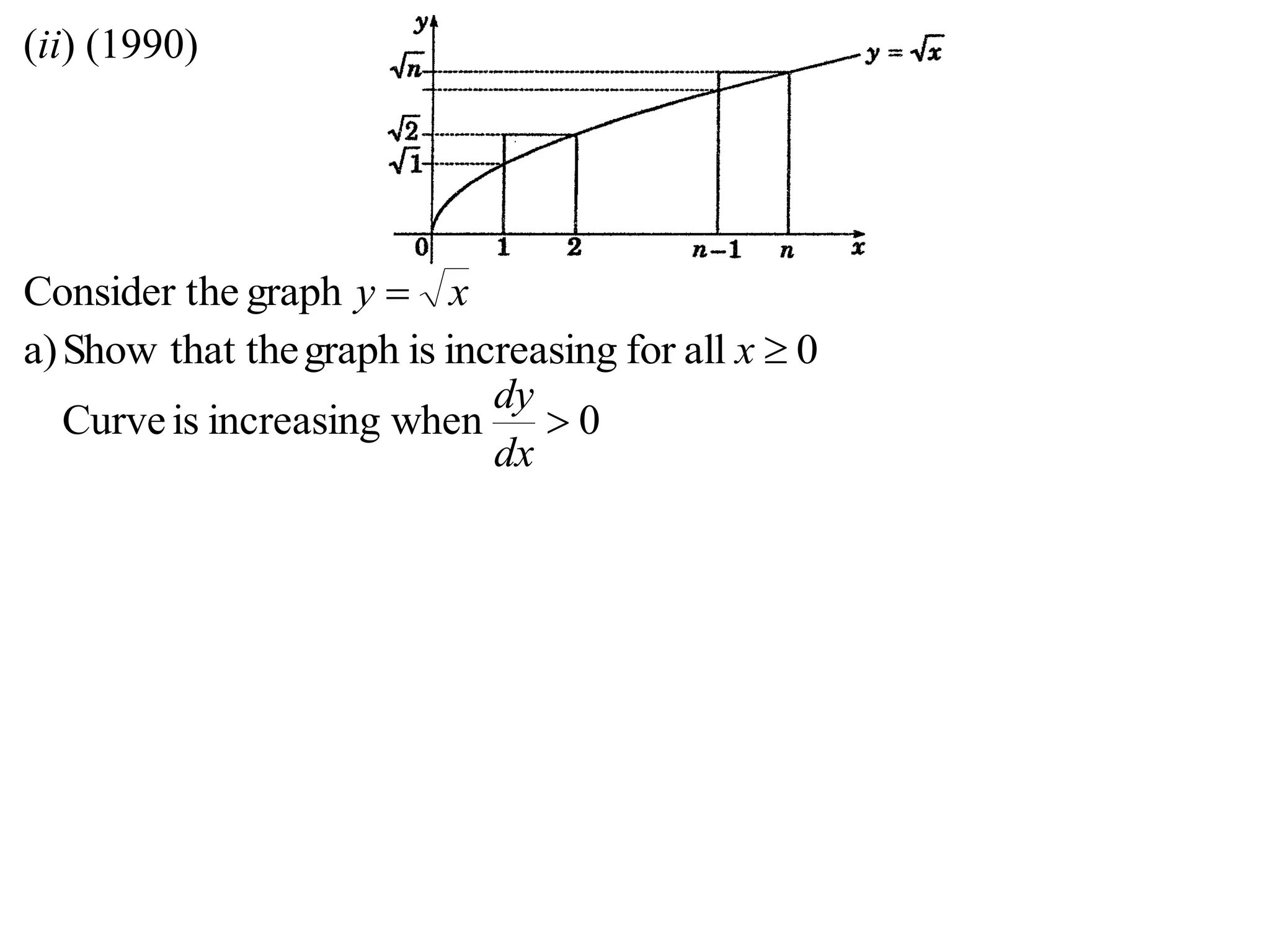
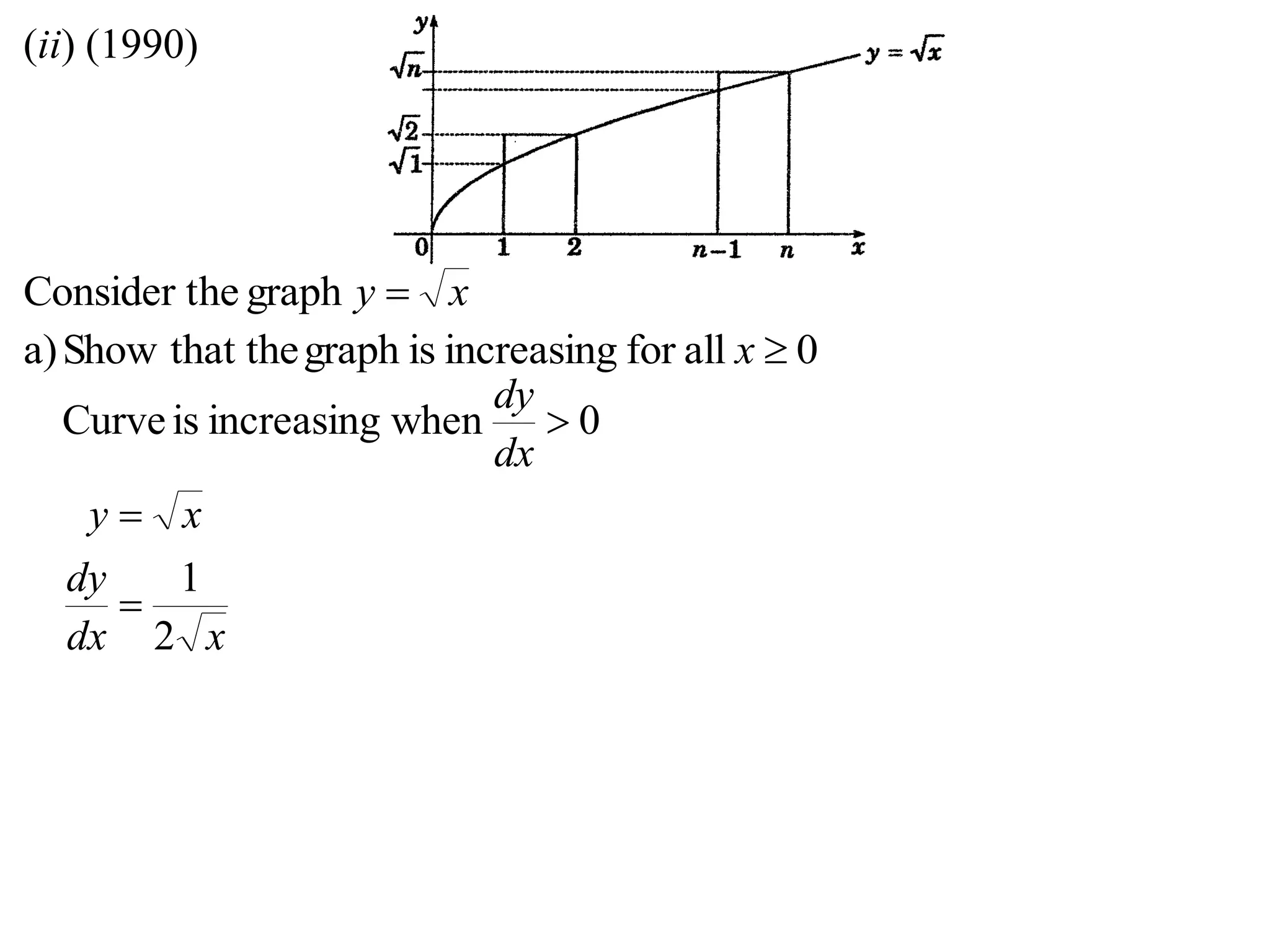
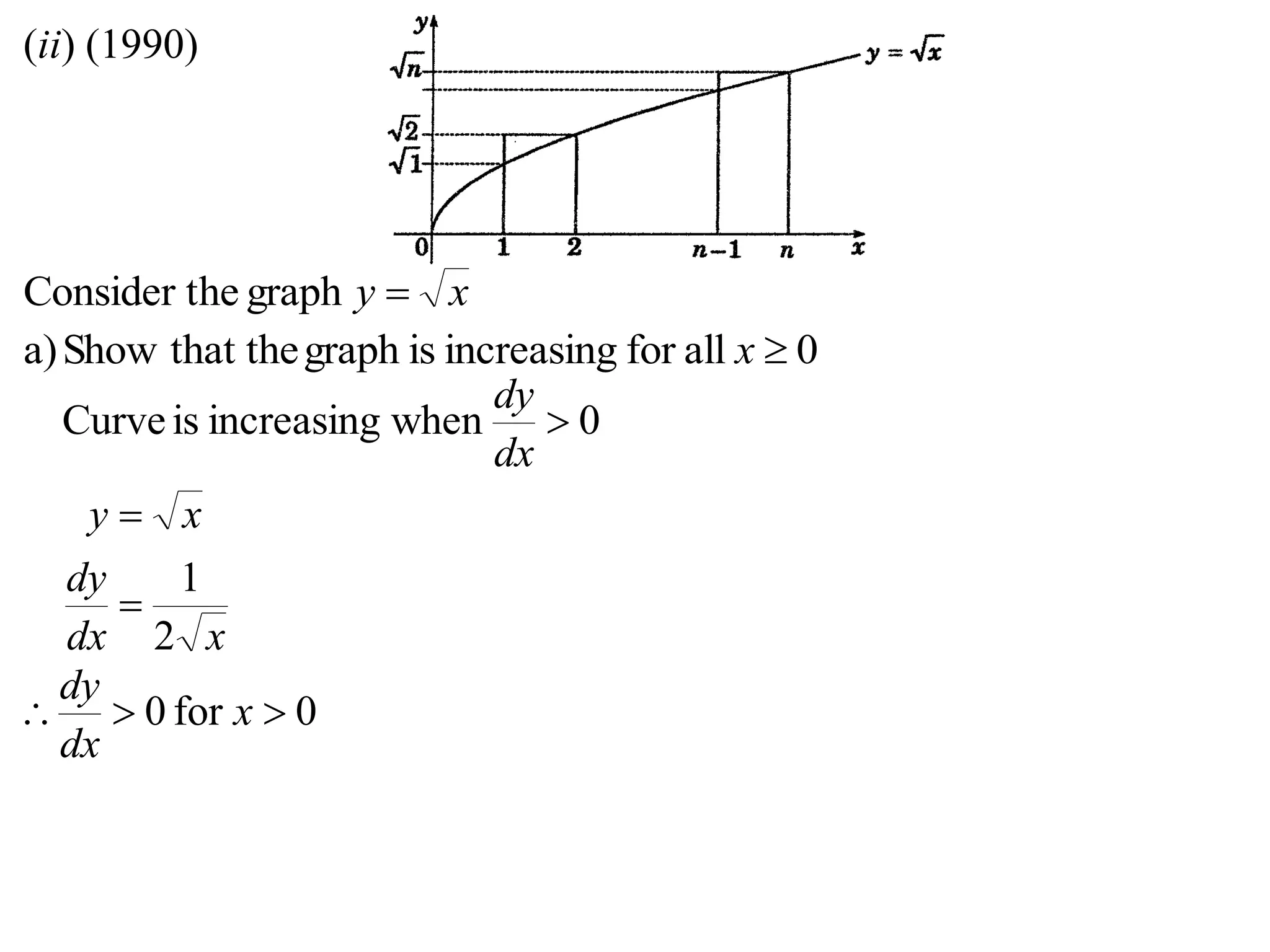
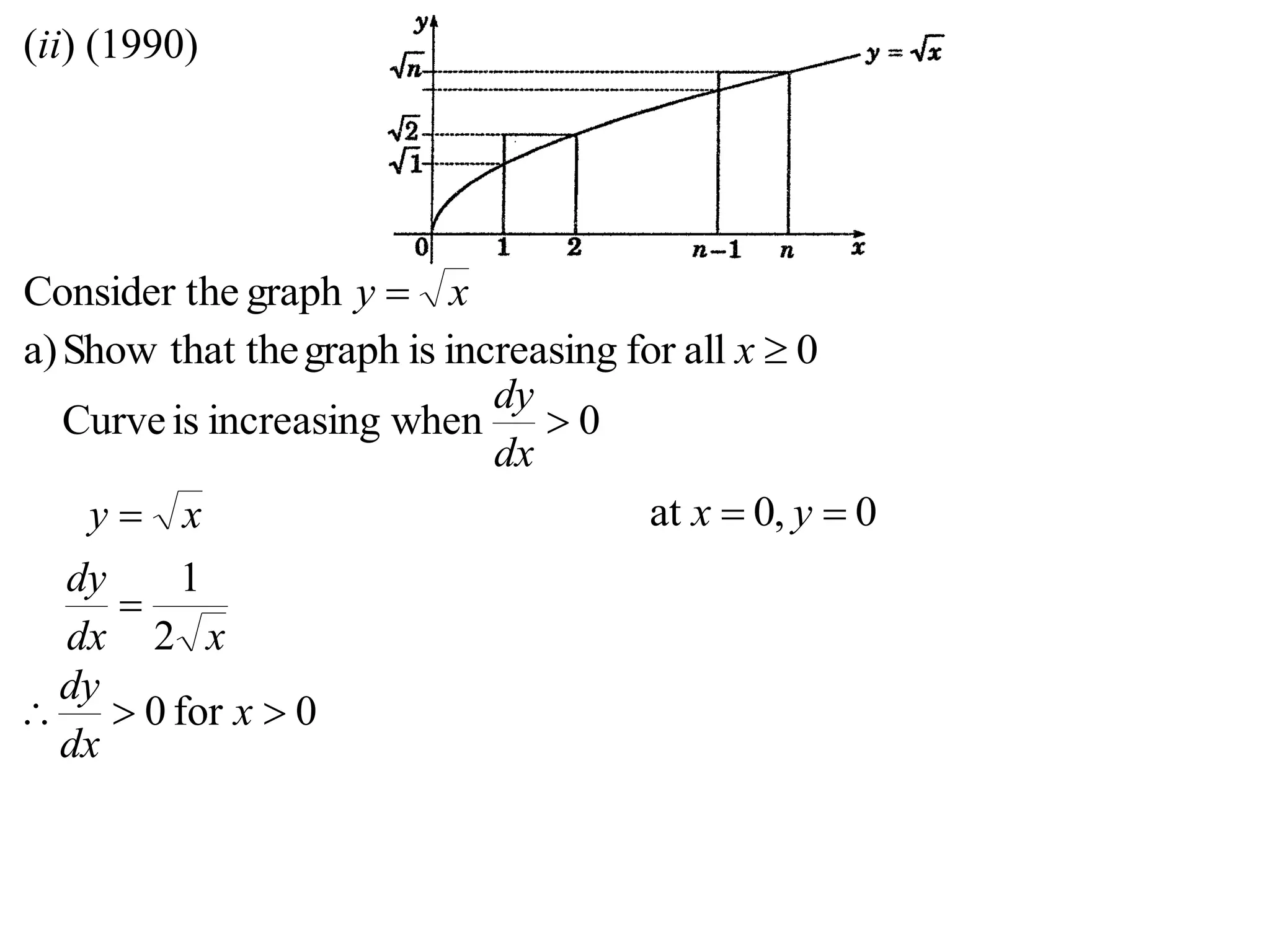
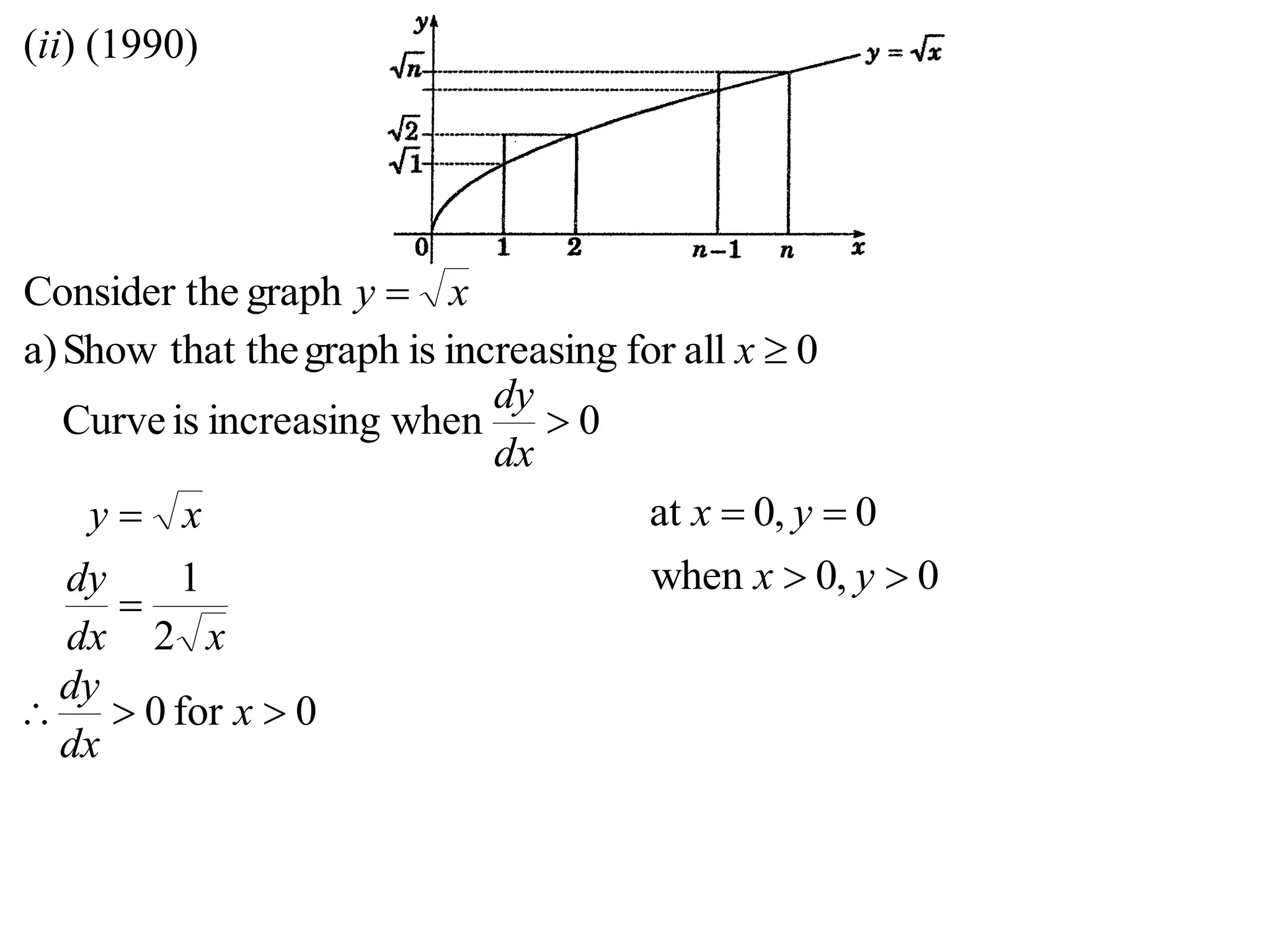
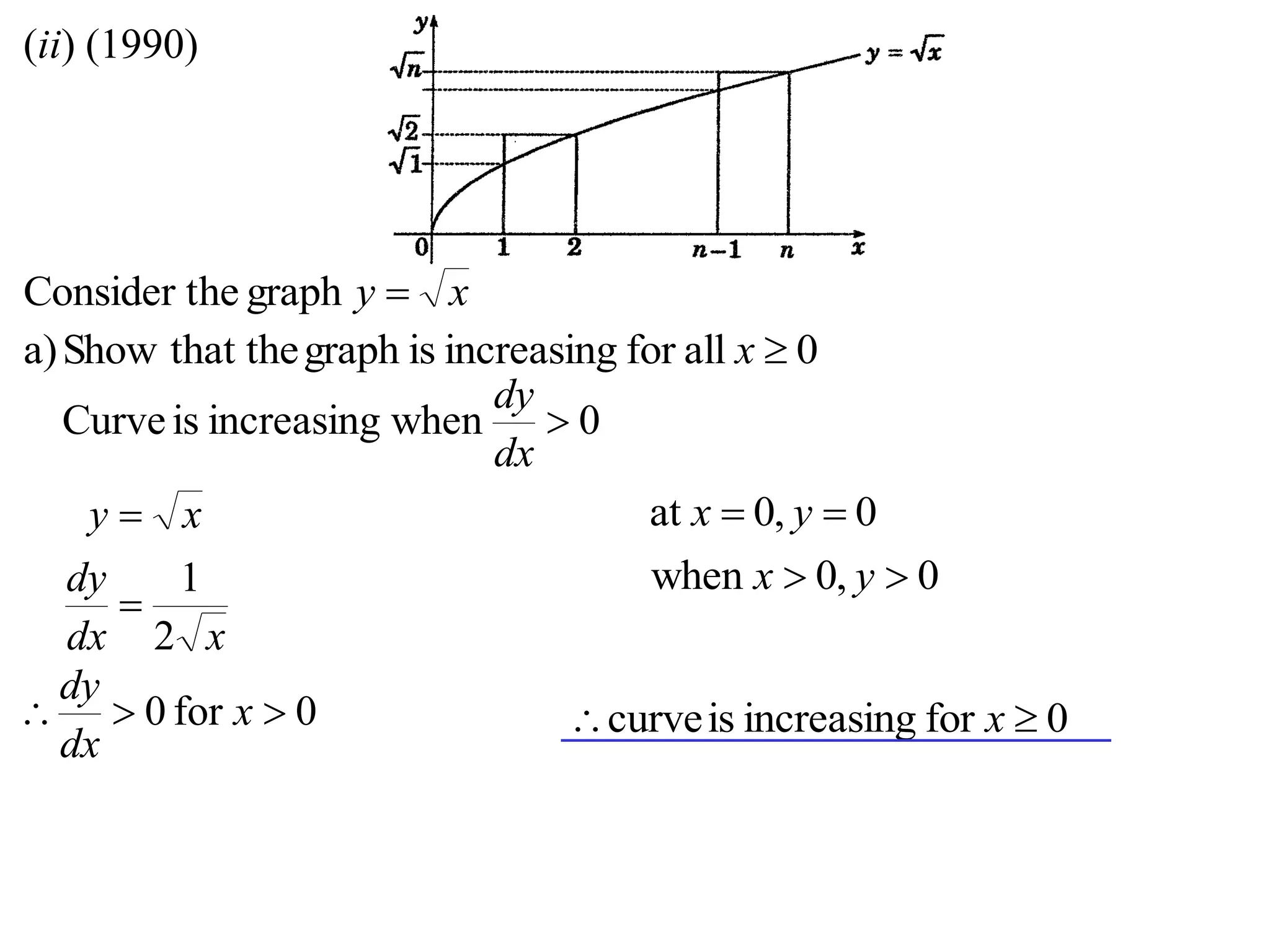
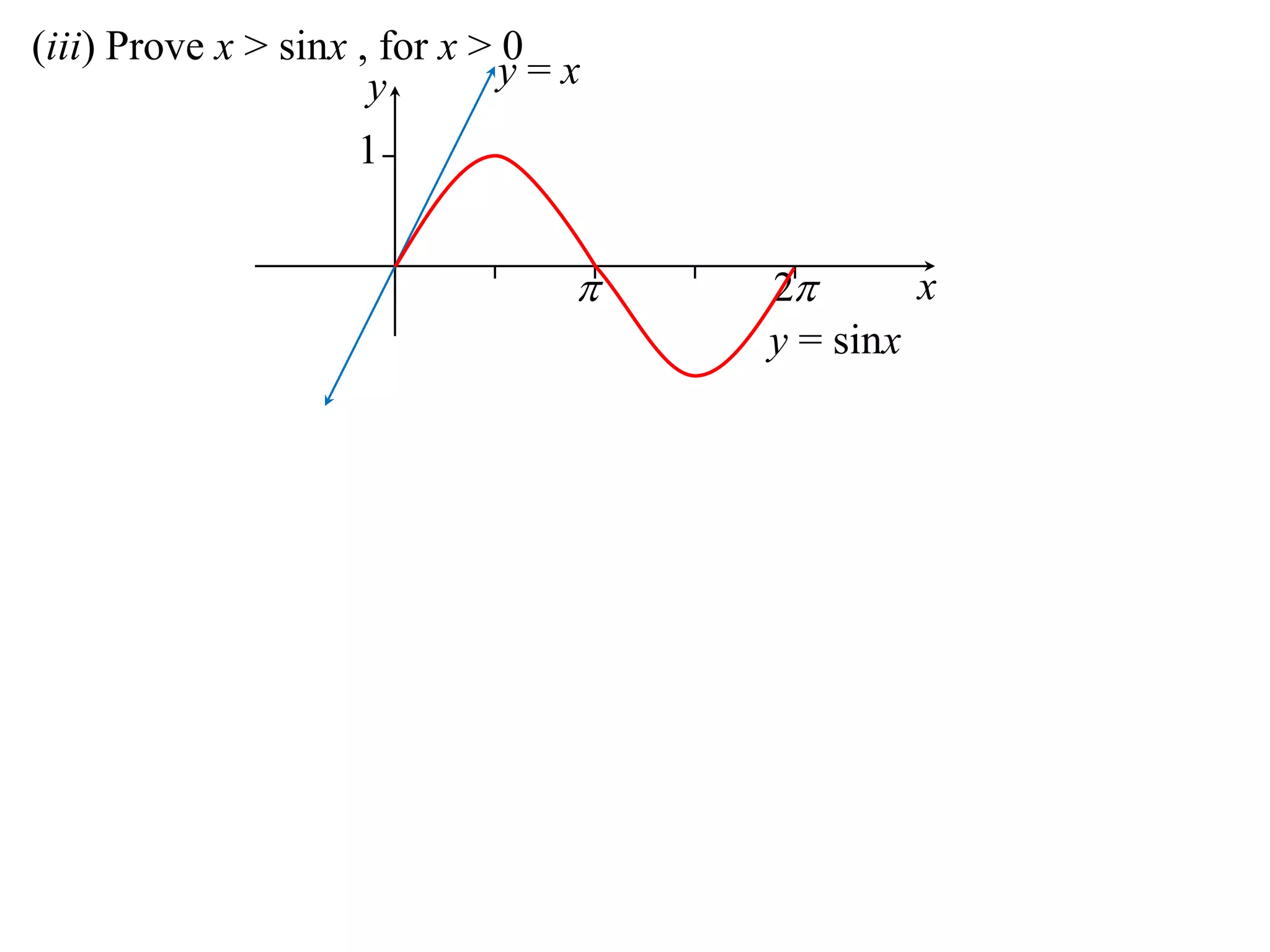
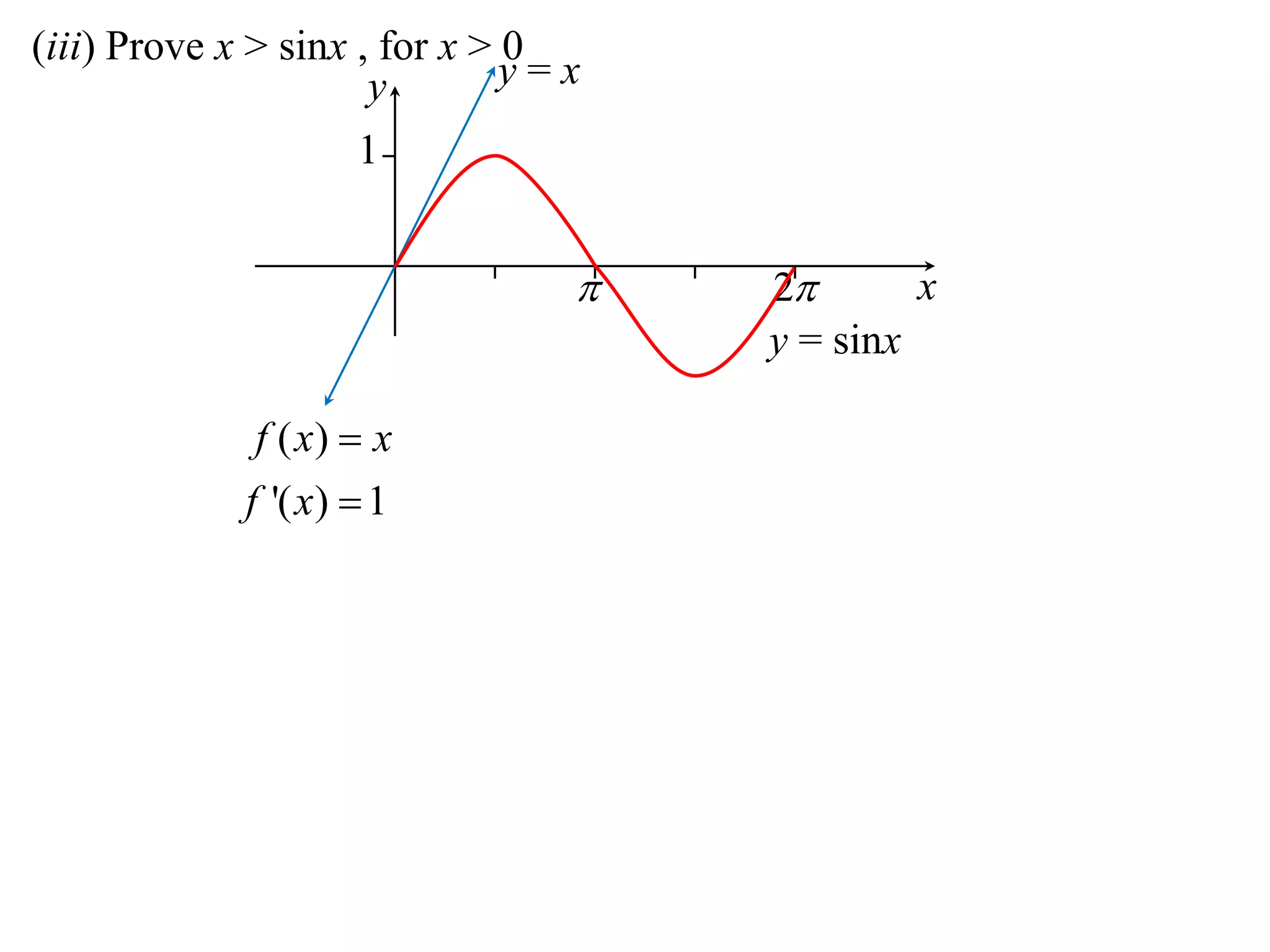
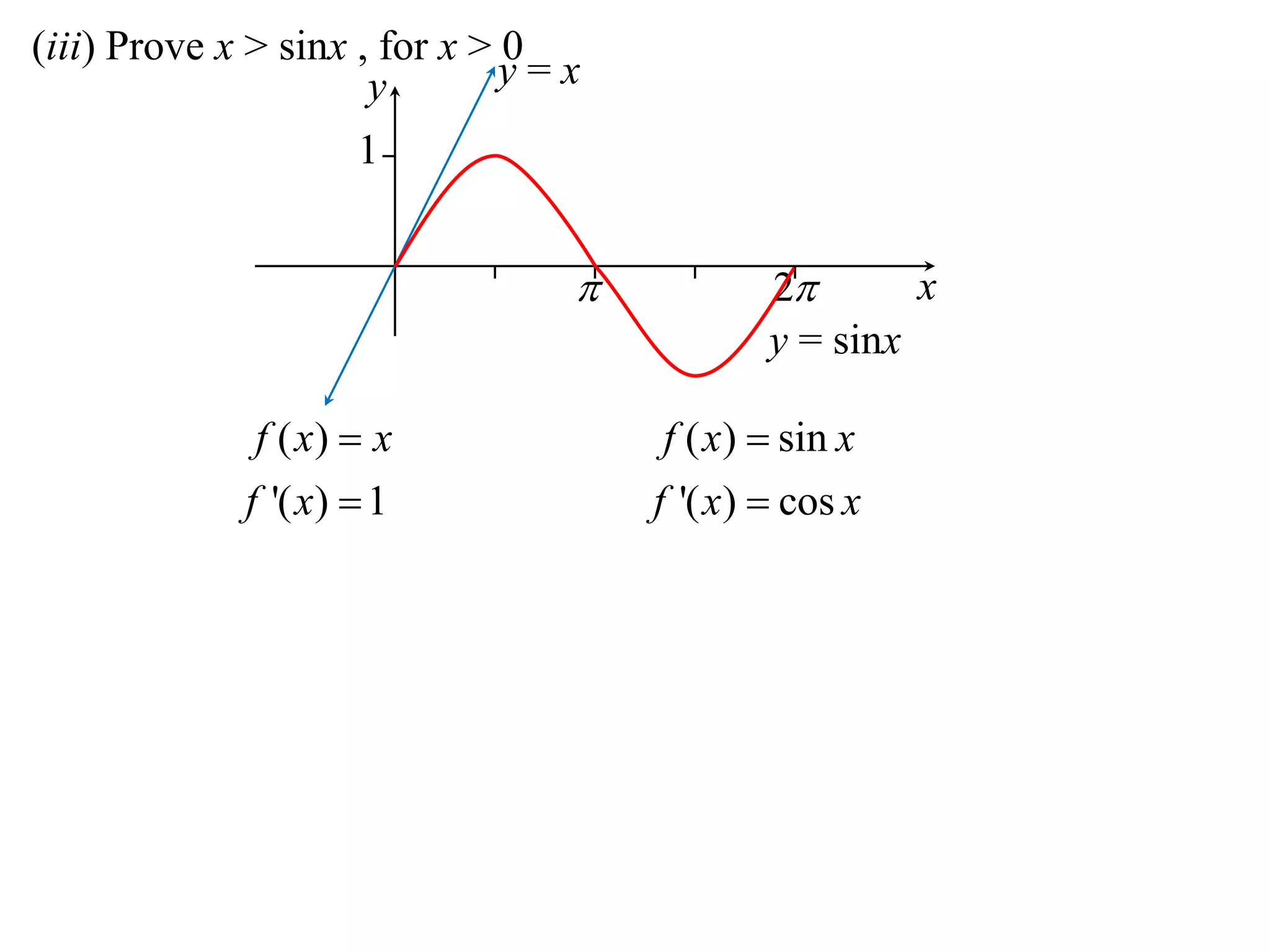
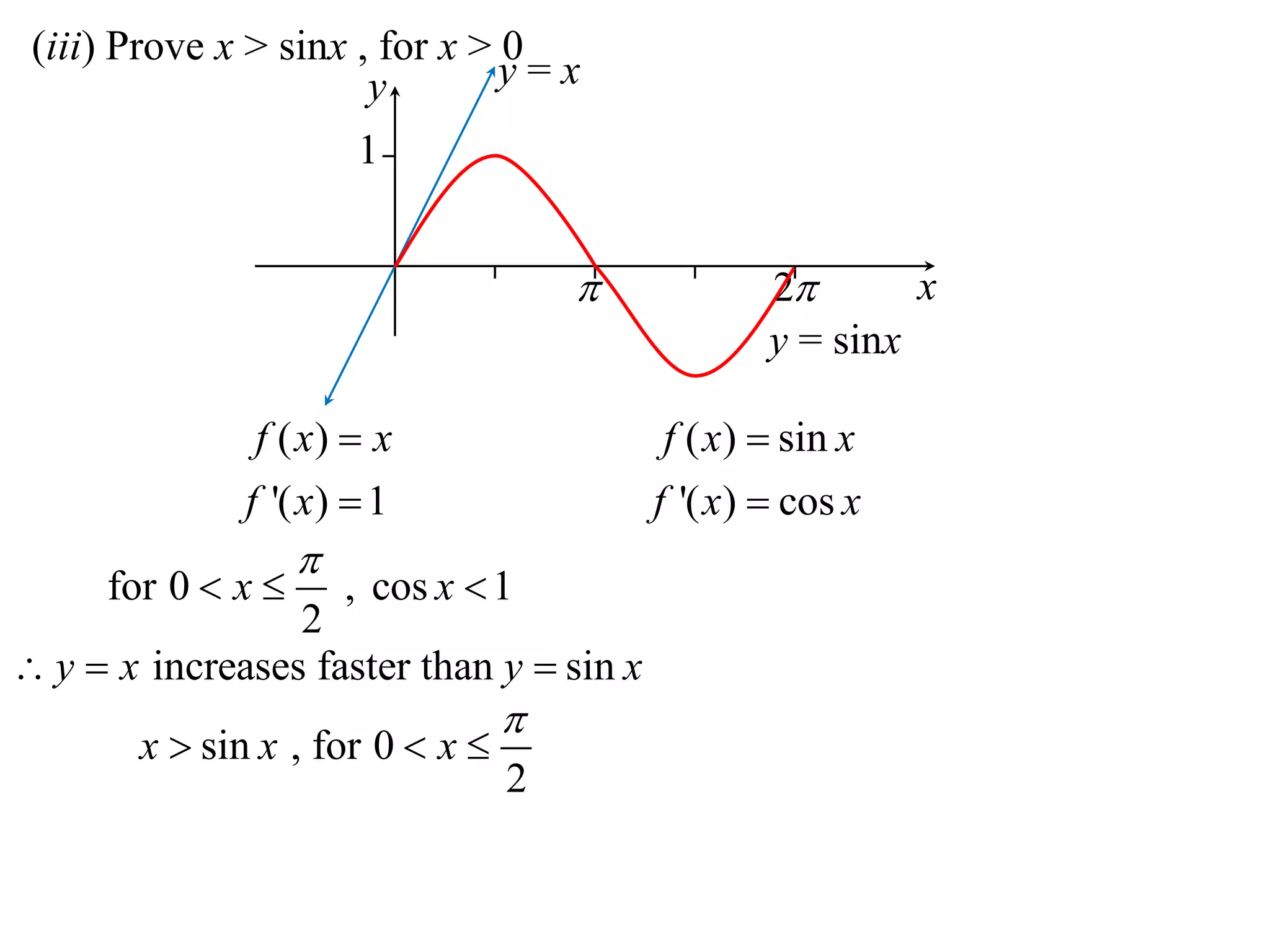
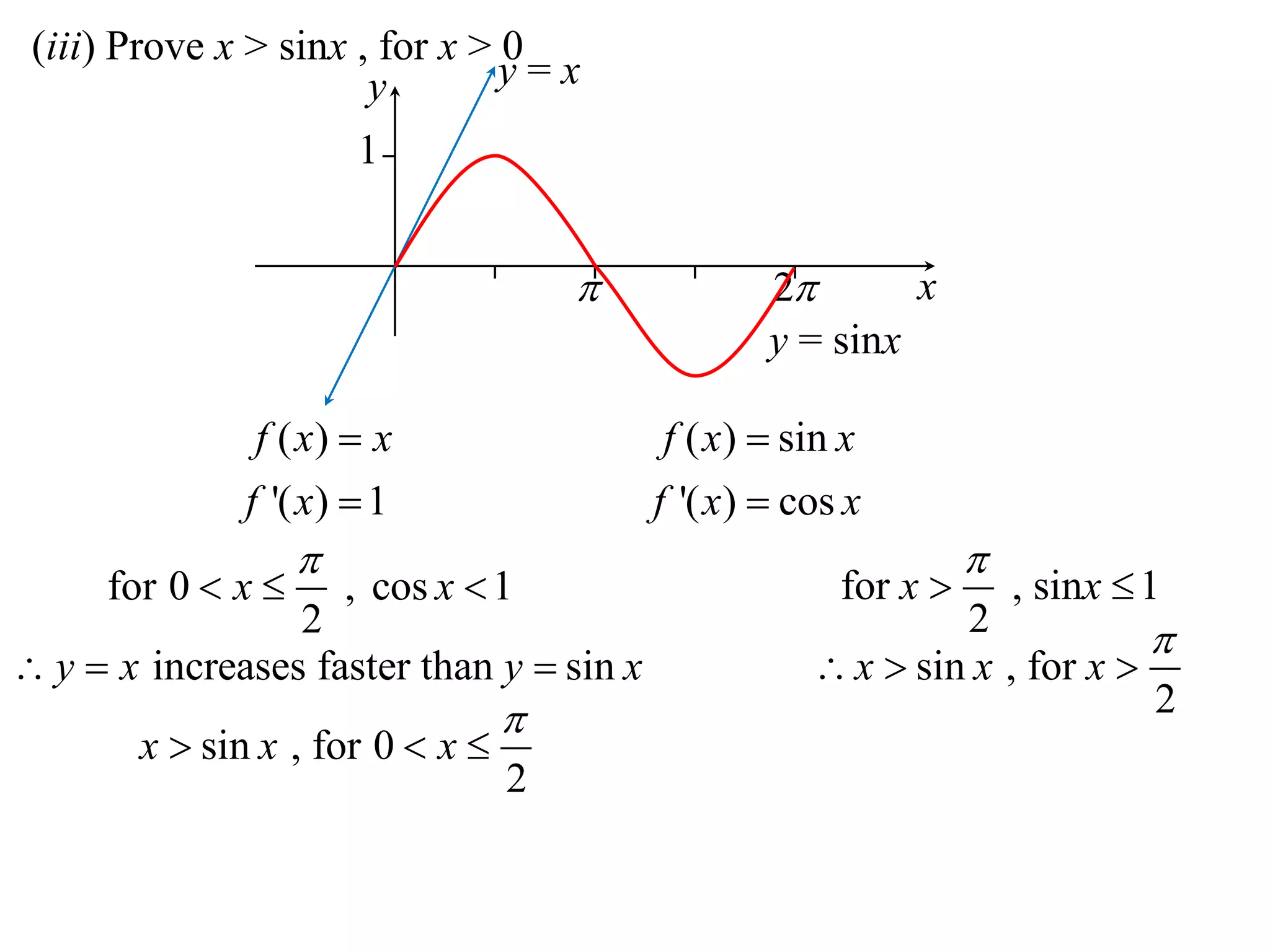
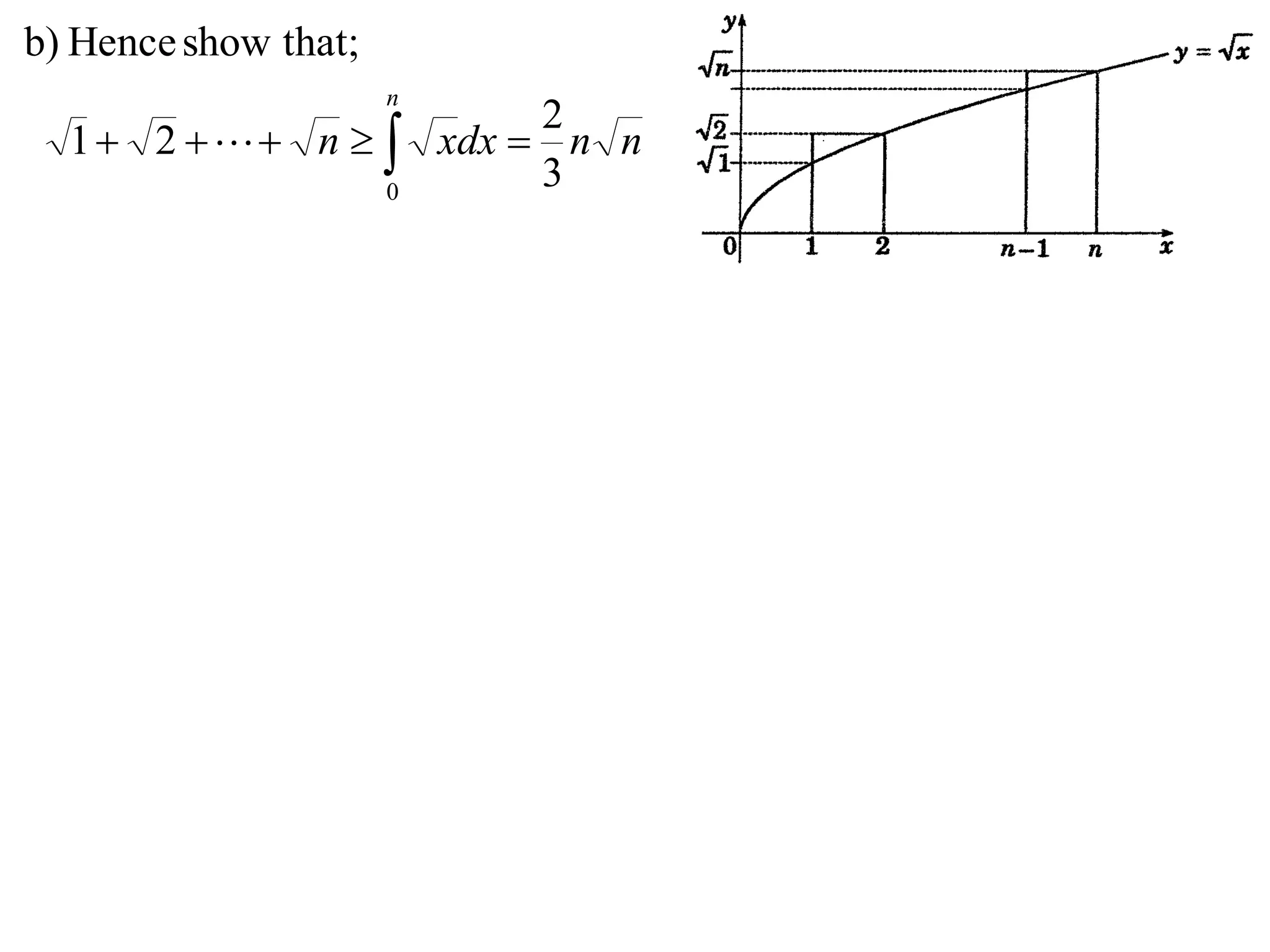
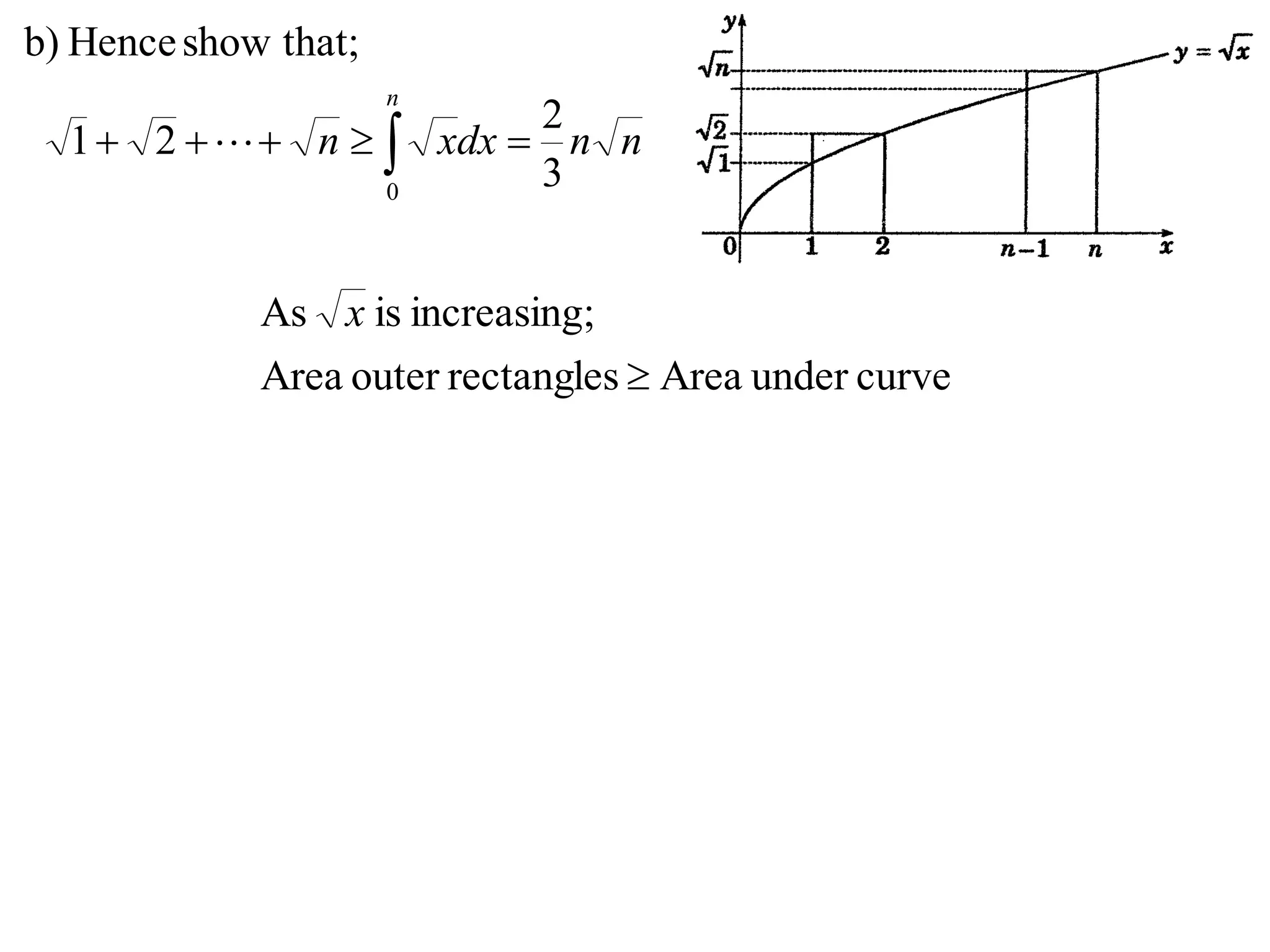
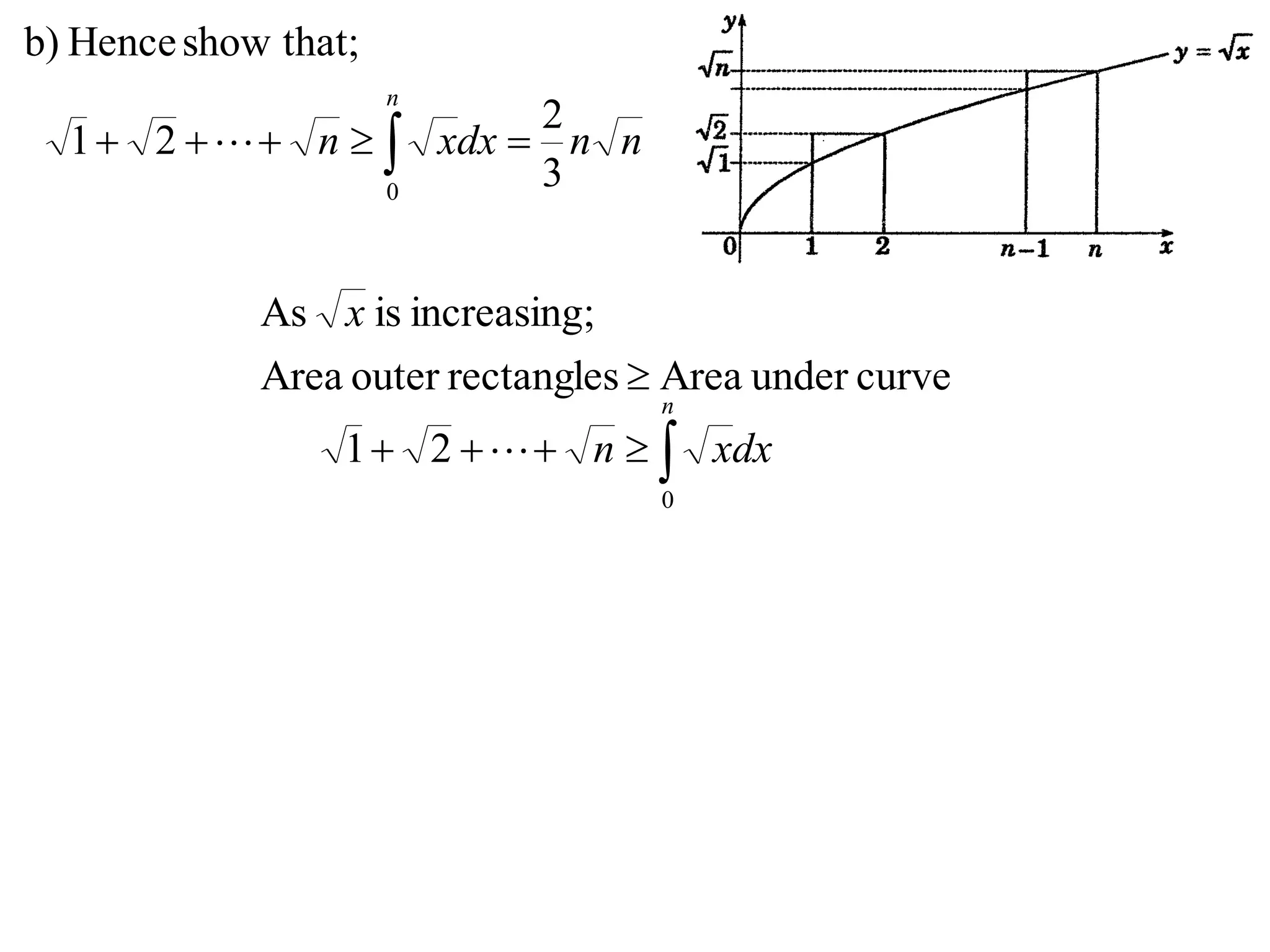
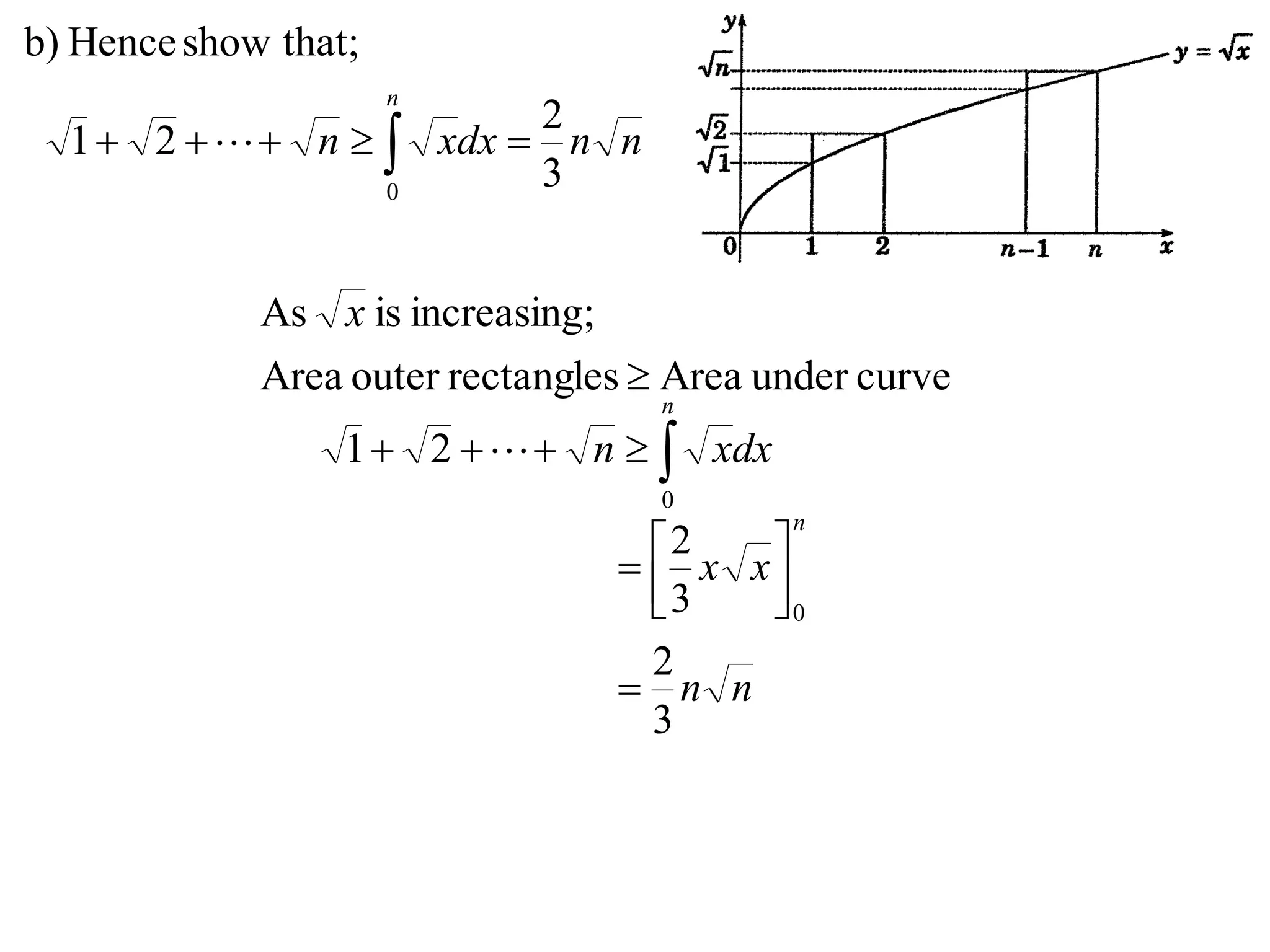
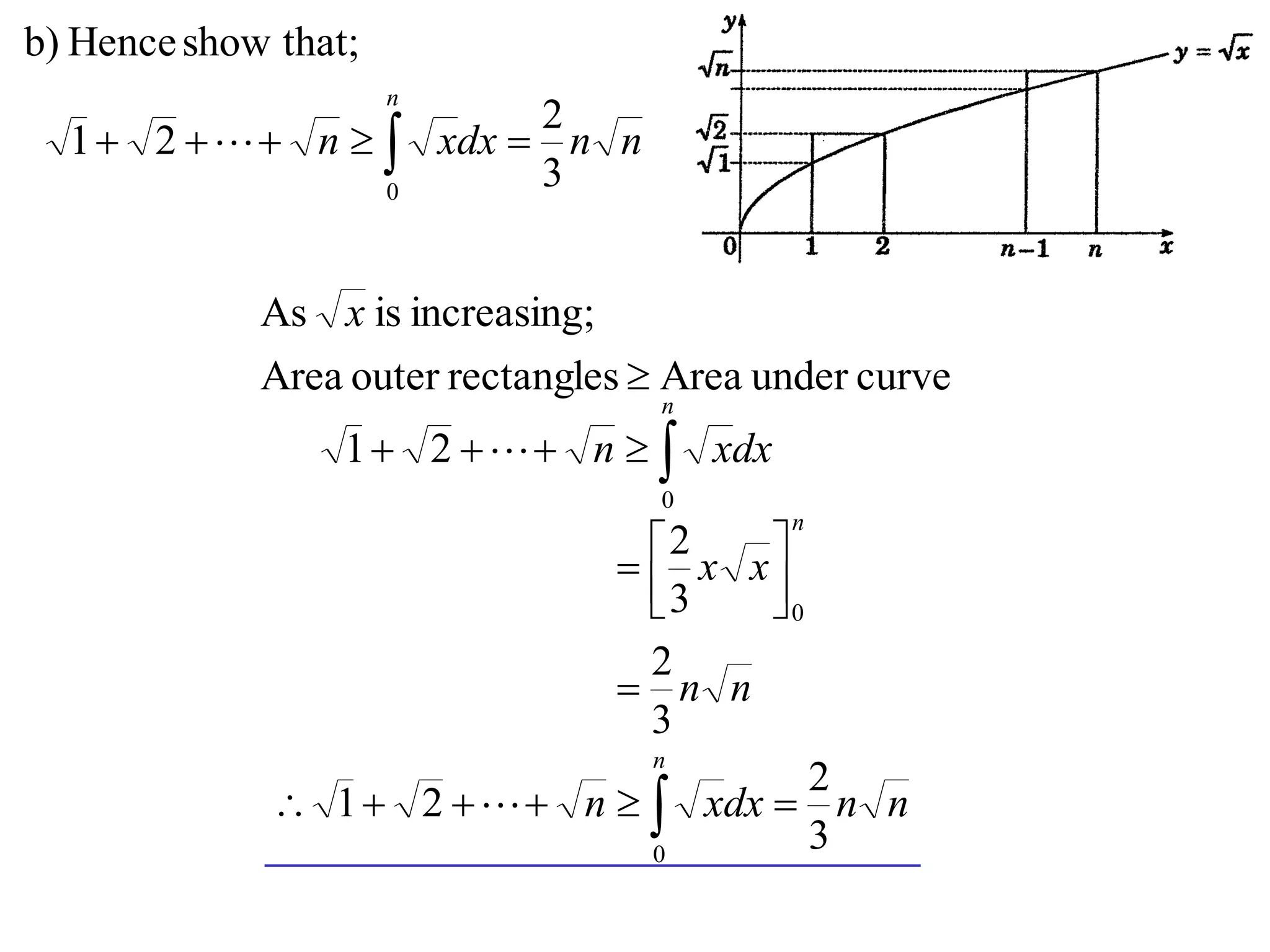
This document discusses inequalities, graphs, and proofs by induction. It contains: 1) Examples of solving inequalities and finding oblique asymptotes of graphs. 2) Considering the graph of y=x and showing various properties, including that it is always increasing and its derivative is always positive. 3) Using integrals to show that the area under the curve is greater than or equal to x. 4) Proving by induction that the sum of the first n positive integers is always between (n^2 + n)/2 and n^2. So in summary, it covers solving inequalities graphically, properties of the line y=x, area under curves, and proofs

1. Inequalities & Graphs

2. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i

3. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i

4. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i

5. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i

6. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i Oblique asymptote:

7. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i
2
4
2
2
2


 x
x
x
x
Oblique asymptote:

8. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i
2
4
2
2
2


 x
x
x
x
Oblique asymptote:

9. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i
2
4
2
2
2


 x
x
x
x
Oblique asymptote:

10. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i

11. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i

12. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i
  
1or2
012
02
2
1
2
2
2
2






xx
xx
xx
xx
x
x

13. Inequalities & Graphs
  1
2
Solvee.g.
2

x
x
i
  
1or2
012
02
2
1
2
2
2
2






xx
xx
xx
xx
x
x
21or2
1
2
2



xx
x
x

14. (ii) (1990)
xy graphheConsider t

15. (ii) (1990)
xy graphheConsider t
0allforincreasingisgraphthat theShowa) x

16. (ii) (1990)
xy graphheConsider t
0allforincreasingisgraphthat theShowa) x
0whenincreasingisCurve 
dx
dy

17. (ii) (1990)
xy graphheConsider t
0allforincreasingisgraphthat theShowa) x
0whenincreasingisCurve 
dx
dy
xdx
dy
xy
2
1



18. (ii) (1990)
xy graphheConsider t
0allforincreasingisgraphthat theShowa) x
0whenincreasingisCurve 
dx
dy
xdx
dy
xy
2
1


0for0  x
dx
dy

19. (ii) (1990)
xy graphheConsider t
0allforincreasingisgraphthat theShowa) x
0whenincreasingisCurve 
dx
dy
xdx
dy
xy
2
1


0for0  x
dx
dy
0,0at  yx

20. (ii) (1990)
xy graphheConsider t
0allforincreasingisgraphthat theShowa) x
0whenincreasingisCurve 
dx
dy
xdx
dy
xy
2
1


0for0  x
dx
dy
0,0at  yx
0,0when  yx

21. (ii) (1990)
xy graphheConsider t
0allforincreasingisgraphthat theShowa) x
0whenincreasingisCurve 
dx
dy
xdx
dy
xy
2
1


0for0  x
dx
dy
0,0at  yx
0,0when  yx
0forincreasingiscurve  x

22.  
n
nndxxn
0
3
2
21
that;showHenceb)


23.  
n
nndxxn
0
3
2
21
that;showHenceb)


24.  
n
nndxxn
0
3
2
21
that;showHenceb)

curveunderArearectanglesouterArea
;increasingisAs

x

25.  
n
nndxxn
0
3
2
21
that;showHenceb)

curveunderArearectanglesouterArea
;increasingisAs

x

n
dxxn
0
21 

26.  
n
nndxxn
0
3
2
21
that;showHenceb)

curveunderArearectanglesouterArea
;increasingisAs

x

n
dxxn
0
21 
nn
xx
n
3
2
3
2
0






27.  
n
nndxxn
0
3
2
21
that;showHenceb)

curveunderArearectanglesouterArea
;increasingisAs

x

n
dxxn
0
21 
nn
xx
n
3
2
3
2
0





 
n
nndxxn
0
3
2
21 

28. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n

29. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1

30. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL

31. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL
 
6
7
1
6
314
..


SHR

32. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL
 
6
7
1
6
314
..


SHR
SHRSHL .... 

33. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL
 
6
7
1
6
314
..


SHR
SHRSHL .... 
Hence the result is true for n = 1

34. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL
 
6
7
1
6
314
..


SHR
SHRSHL .... 
Hence the result is true for n = 1
integerpositiveaiswherefortrueisresulttheAssume kkn 

35. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL
 
6
7
1
6
314
..


SHR
SHRSHL .... 
Hence the result is true for n = 1
integerpositiveaiswherefortrueisresulttheAssume kkn 
k
k
k
6
34
21i.e.

 

36. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL
 
6
7
1
6
314
..


SHR
SHRSHL .... 
Hence the result is true for n = 1
integerpositiveaiswherefortrueisresulttheAssume kkn 
k
k
k
6
34
21i.e.

 
1fortrueisresulttheProve  kn

37. 1integersallfor
6
34
21
that;showtoinductionalmathematicUsec)


 nn
n
n
Test: n = 1
1
1..

SHL
 
6
7
1
6
314
..


SHR
SHRSHL .... 
Hence the result is true for n = 1
integerpositiveaiswherefortrueisresulttheAssume kkn 
k
k
k
6
34
21i.e.

 
1fortrueisresulttheProve  kn
1
6
74
121Provei.e. 

 k
k
k

38. Proof:

39. Proof: 121121  kkk 

40. Proof: 121121  kkk 
1
6
34


 kk
k

41. Proof: 121121  kkk 
1
6
34


 kk
k
 
6
1634
2


kkk

42. Proof: 121121  kkk 
1
6
34


 kk
k
 
6
1634
2


kkk
6
1692416 23


kkkk

43. Proof: 121121  kkk 
1
6
34


 kk
k
 
6
1634
2


kkk
6
1692416 23


kkkk
  
6
16118161 2


kkkk

44. Proof: 121121  kkk 
1
6
34


 kk
k
 
6
1634
2


kkk
6
1692416 23


kkkk
  
6
16118161 2


kkkk
  
6
161141
2


kkk

45. Proof: 121121  kkk 
1
6
34


 kk
k
 
6
1634
2


kkk
6
1692416 23


kkkk
  
6
16118161 2


kkkk
  
6
161141
2


kkk
  
6
16141
2


kkk

46. Proof: 121121  kkk 
1
6
34


 kk
k
 
6
1634
2


kkk
6
1692416 23


kkkk
  
6
16118161 2


kkkk
  
6
161141
2


kkk
  
6
16141
2


kkk
   
   
6
174
6
16114




kk
kkk

47. Hence the result is true for n = k +1 if it is also true for n =k

48. Hence the result is true for n = k +1 if it is also true for n =k
Since the result is true for n = 1 then it is also true for n =1+1 i.e. n=2,
and since the result is true for n = 2 then it is also true for n =2+1 i.e.
n=3, and so on for all positive integral values of n

49. Hence the result is true for n = k +1 if it is also true for n =k
Since the result is true for n = 1 then it is also true for n =1+1 i.e. n=2,
and since the result is true for n = 2 then it is also true for n =2+1 i.e.
n=3, and so on for all positive integral values of n
hundrednearesttheto1000021
estimate;toc)andb)Used)
 

50. Hence the result is true for n = k +1 if it is also true for n =k
Since the result is true for n = 1 then it is also true for n =1+1 i.e. n=2,
and since the result is true for n = 2 then it is also true for n =2+1 i.e.
n=3, and so on for all positive integral values of n
hundrednearesttheto1000021
estimate;toc)andb)Used)
 
n
n
nnn
6
34
21
3
2 
 

51. Hence the result is true for n = k +1 if it is also true for n =k
Since the result is true for n = 1 then it is also true for n =1+1 i.e. n=2,
and since the result is true for n = 2 then it is also true for n =2+1 i.e.
n=3, and so on for all positive integral values of n
hundrednearesttheto1000021
estimate;toc)andb)Used)
 
n
n
nnn
6
34
21
3
2 
 
 
 
10000
6
3100004
10000211000010000
3
2 
 

52. Hence the result is true for n = k +1 if it is also true for n =k
Since the result is true for n = 1 then it is also true for n =1+1 i.e. n=2,
and since the result is true for n = 2 then it is also true for n =2+1 i.e.
n=3, and so on for all positive integral values of n
hundrednearesttheto1000021
estimate;toc)andb)Used)
 
n
n
nnn
6
34
21
3
2 
 
 
 
10000
6
3100004
10000211000010000
3
2 
 
6667001000021666700  

53. Hence the result is true for n = k +1 if it is also true for n =k
Since the result is true for n = 1 then it is also true for n =1+1 i.e. n=2,
and since the result is true for n = 2 then it is also true for n =2+1 i.e.
n=3, and so on for all positive integral values of n
hundrednearesttheto1000021
estimate;toc)andb)Used)
 
n
n
nnn
6
34
21
3
2 
 
 
 
10000
6
3100004
10000211000010000
3
2 
 
6667001000021666700  
hundrednearesttheto6667001000021  

54. (iii) Prove x > sinx , for x > 0

55. (iii) Prove x > sinx , for x > 0
1
y
x 2
y = x
y = sinx

56. (iii) Prove x > sinx , for x > 0
1
y
x 2
y = x
y = sinx
( )
'( ) 1
f x x
f x



57. (iii) Prove x > sinx , for x > 0
1
y
x 2
y = x
y = sinx
( )
'( ) 1
f x x
f x


( ) sin
'( ) cos
f x x
f x x



58. (iii) Prove x > sinx , for x > 0
1
y
x 2
y = x
y = sinx
( )
'( ) 1
f x x
f x


( ) sin
'( ) cos
f x x
f x x


for 0 , cos 1
2
x x

  
increases faster than siny x y x  
sin , for 0
2
x x x

  

59. (iii) Prove x > sinx , for x > 0
1
y
x 2
y = x
y = sinx
( )
'( ) 1
f x x
f x


( ) sin
'( ) cos
f x x
f x x


for 0 , cos 1
2
x x

  
increases faster than siny x y x  
sin , for 0
2
x x x

  
for , sin 1
2
x x

 
sin , for
2
x x x

  

60. (iii) Prove x > sinx , for x > 0
1
y
x 2
y = x
y = sinx
( )
'( ) 1
f x x
f x


( ) sin
'( ) cos
f x x
f x x


for 0 , cos 1
2
x x

  
increases faster than siny x y x  
sin , for 0
2
x x x

  
for , sin 1
2
x x

 
sin , for
2
x x x

  
sin , for 0x x x  

61. (iii) Prove x > sinx , for x > 0
1
y
x 2
y = x
y = sinx
( )
'( ) 1
f x x
f x


( ) sin
'( ) cos
f x x
f x x


for 0 , cos 1
2
x x

  
increases faster than siny x y x  
sin , for 0
2
x x x

  
for , sin 1
2
x x

 
sin , for
2
x x x

  
sin , for 0x x x   Exercise 10F