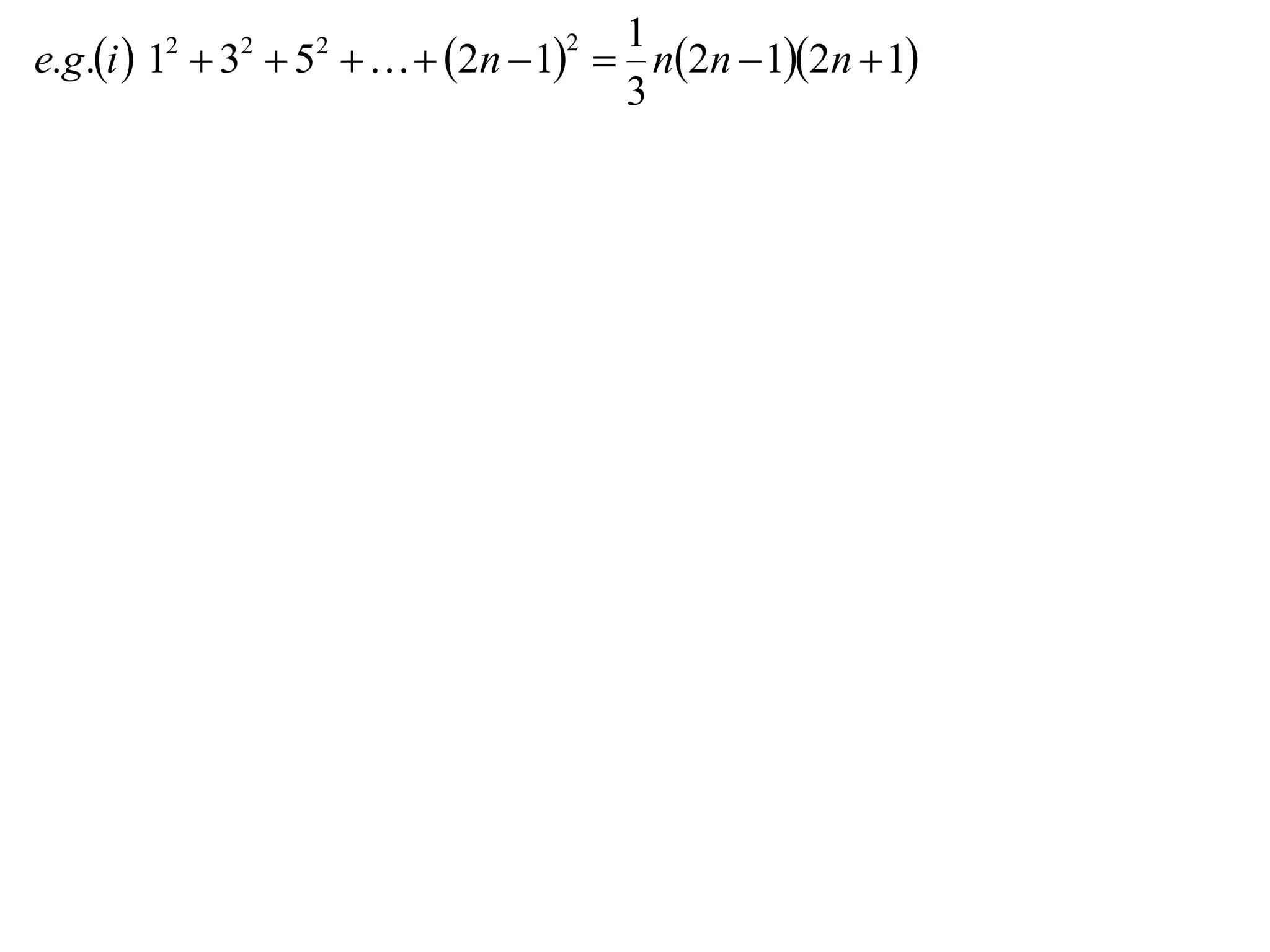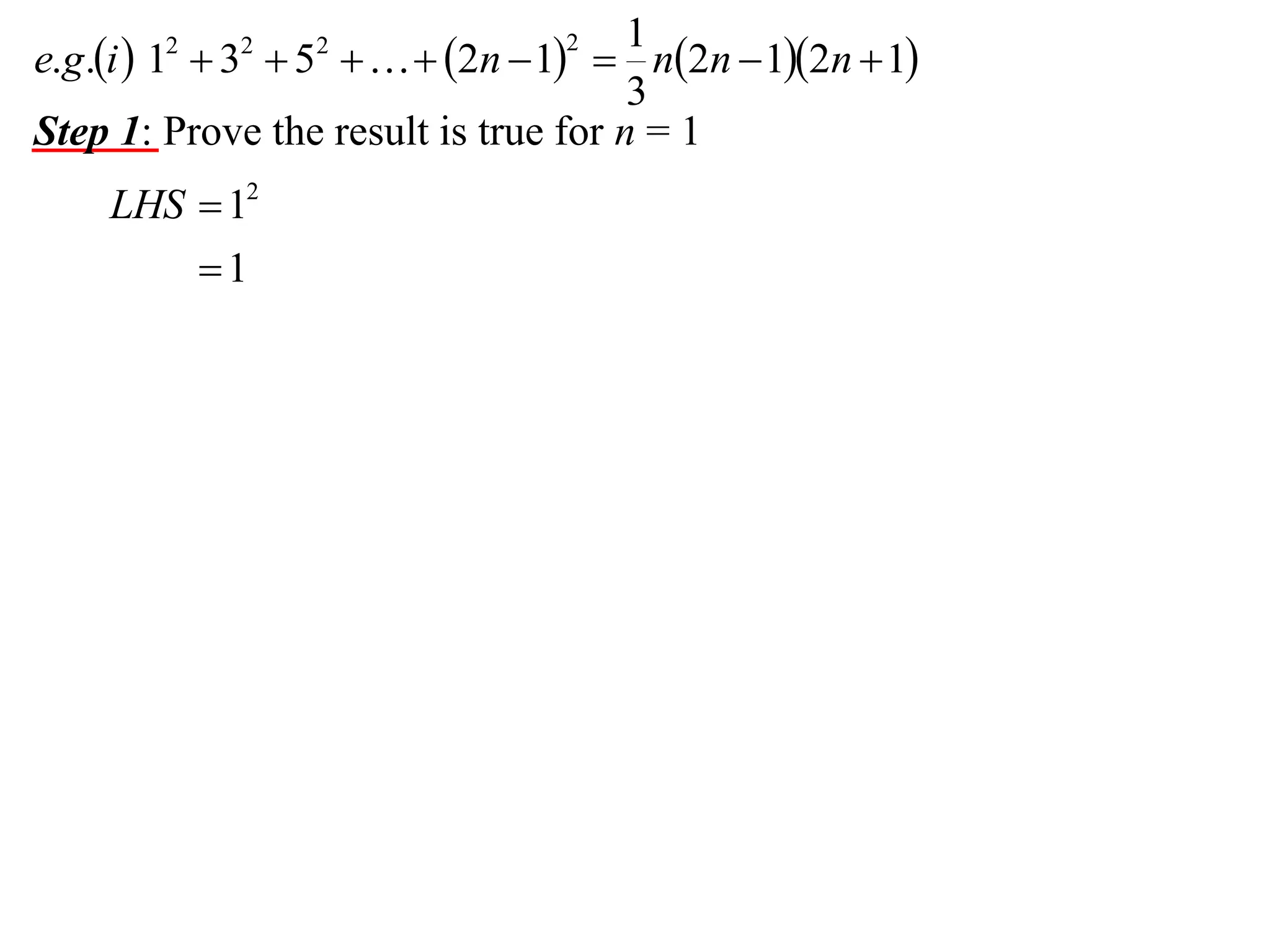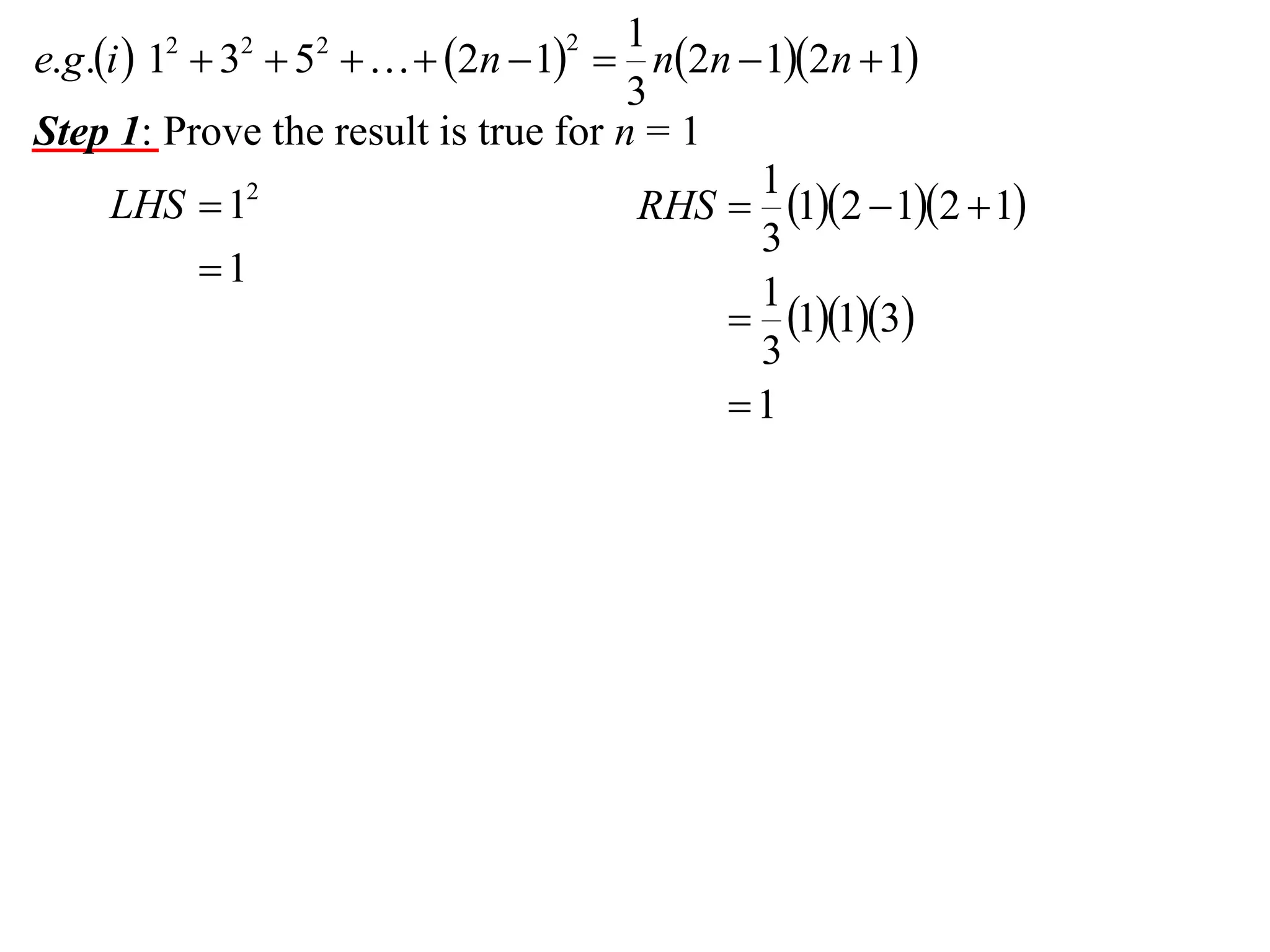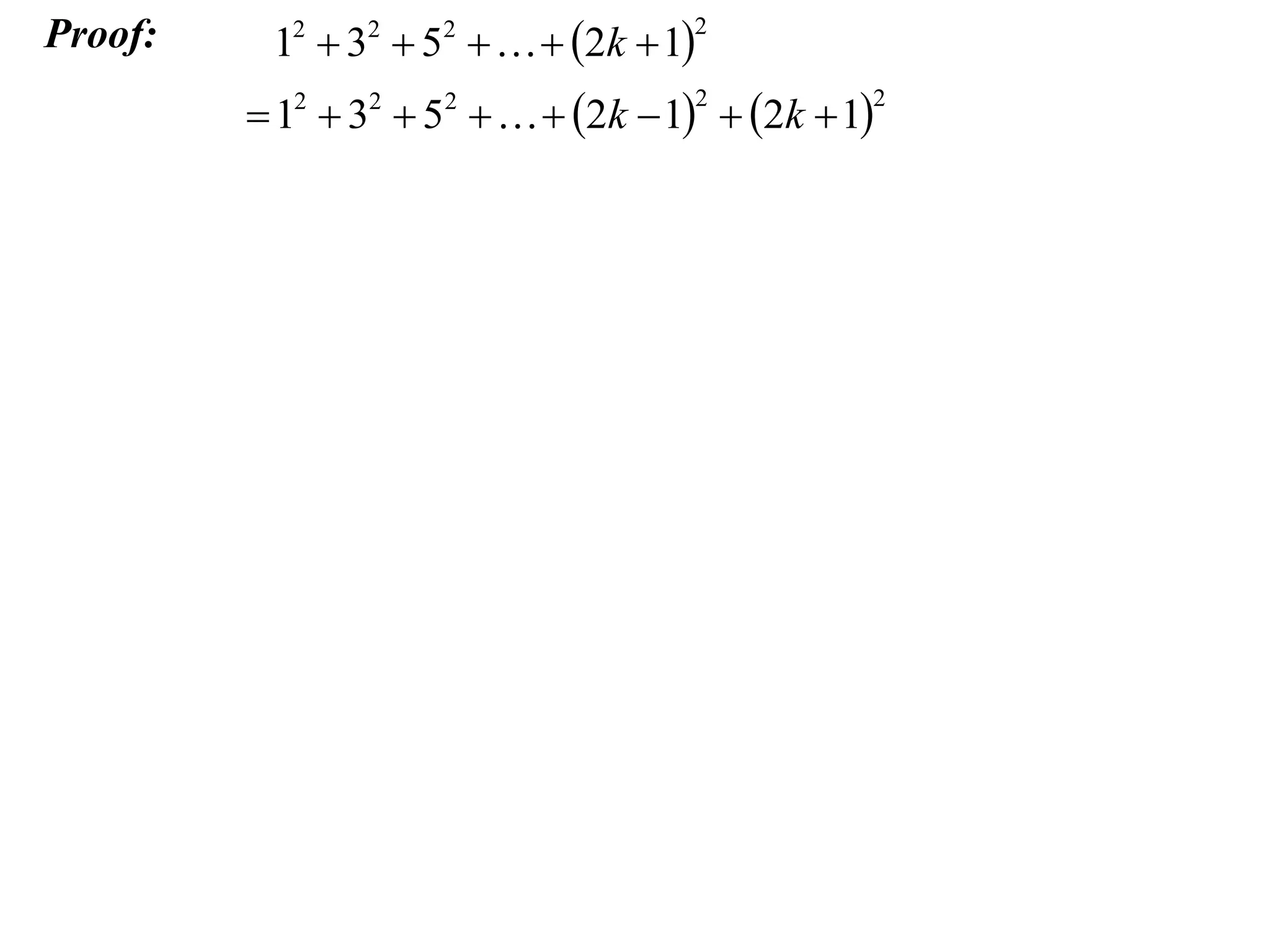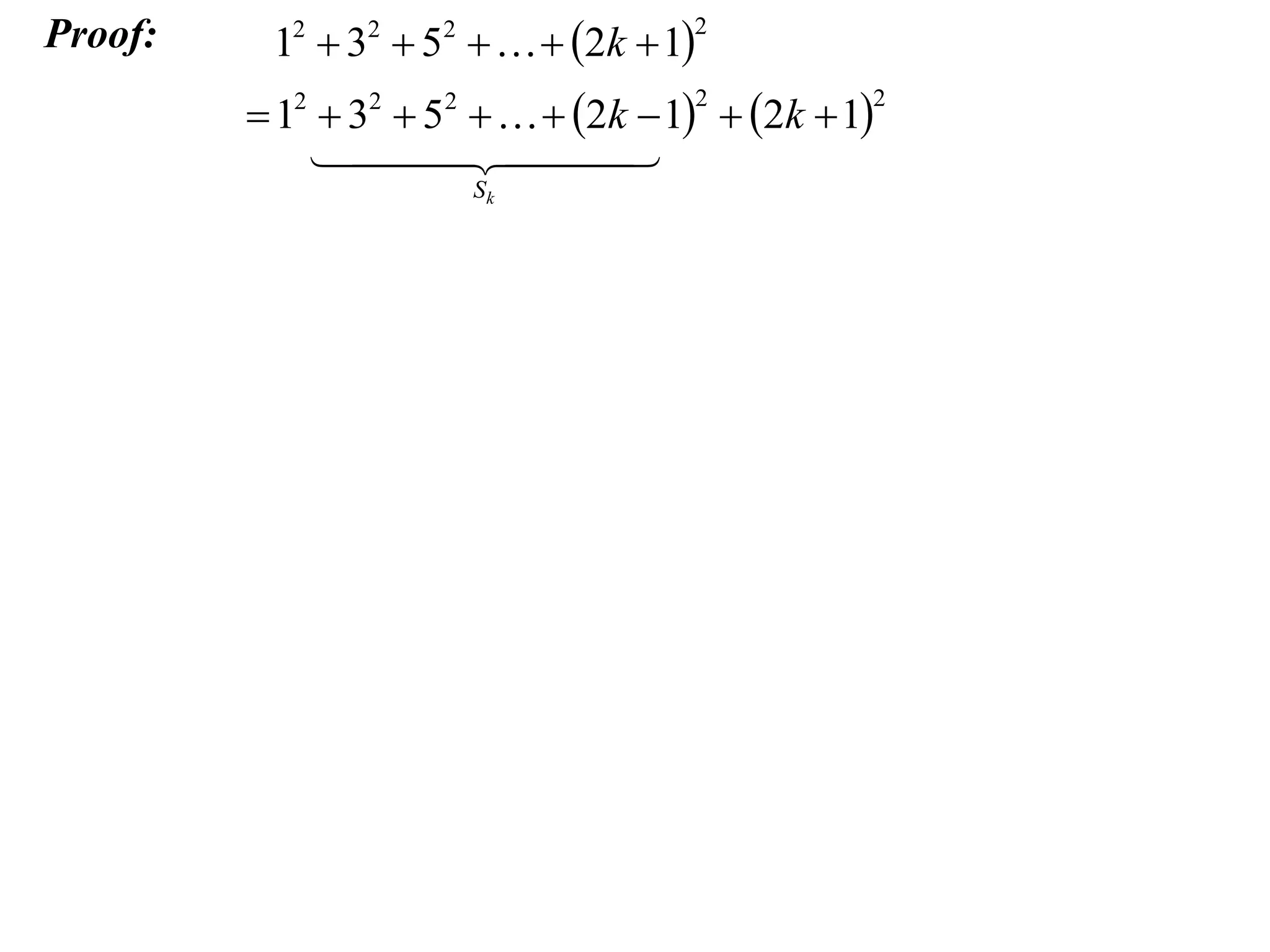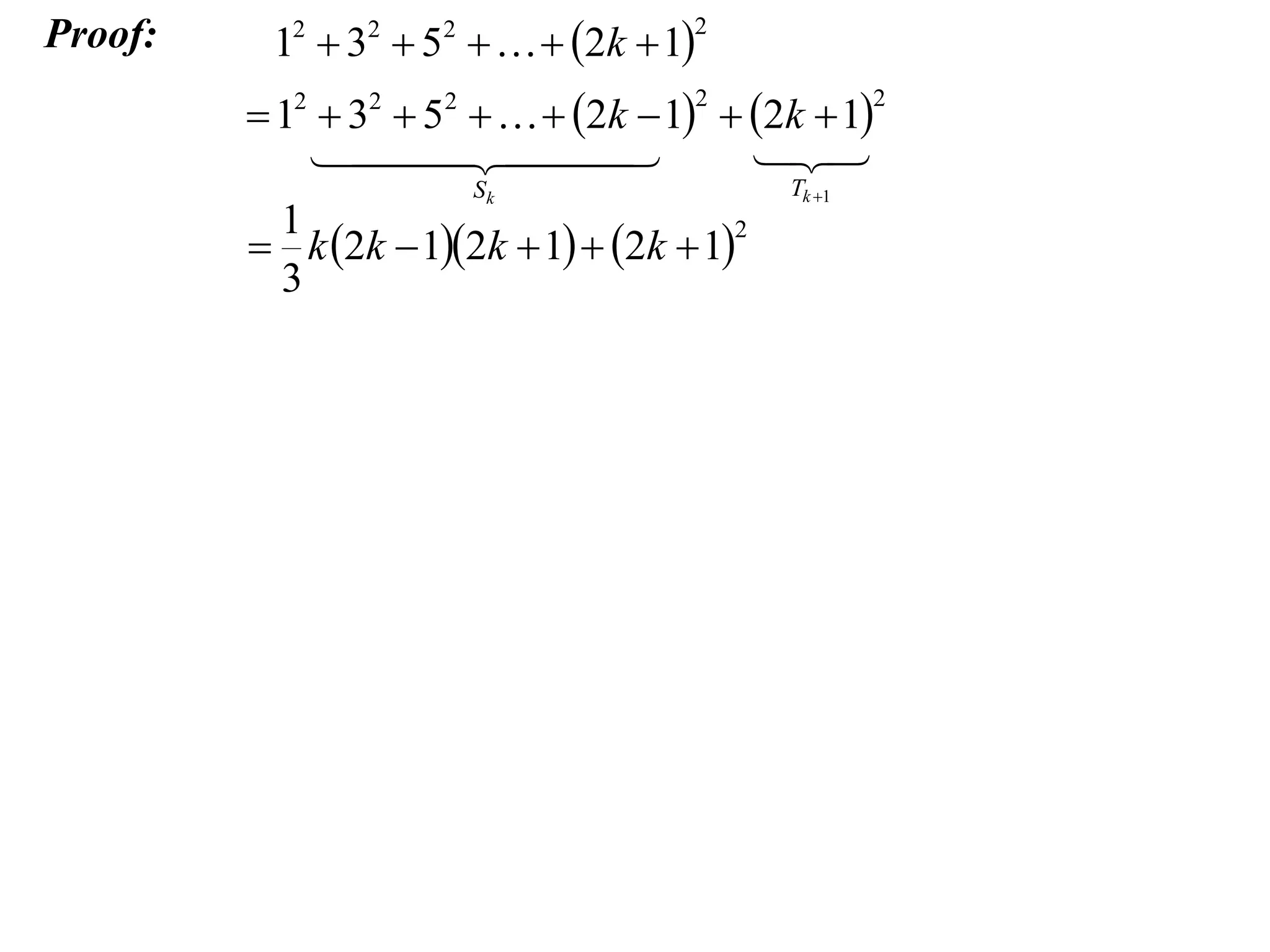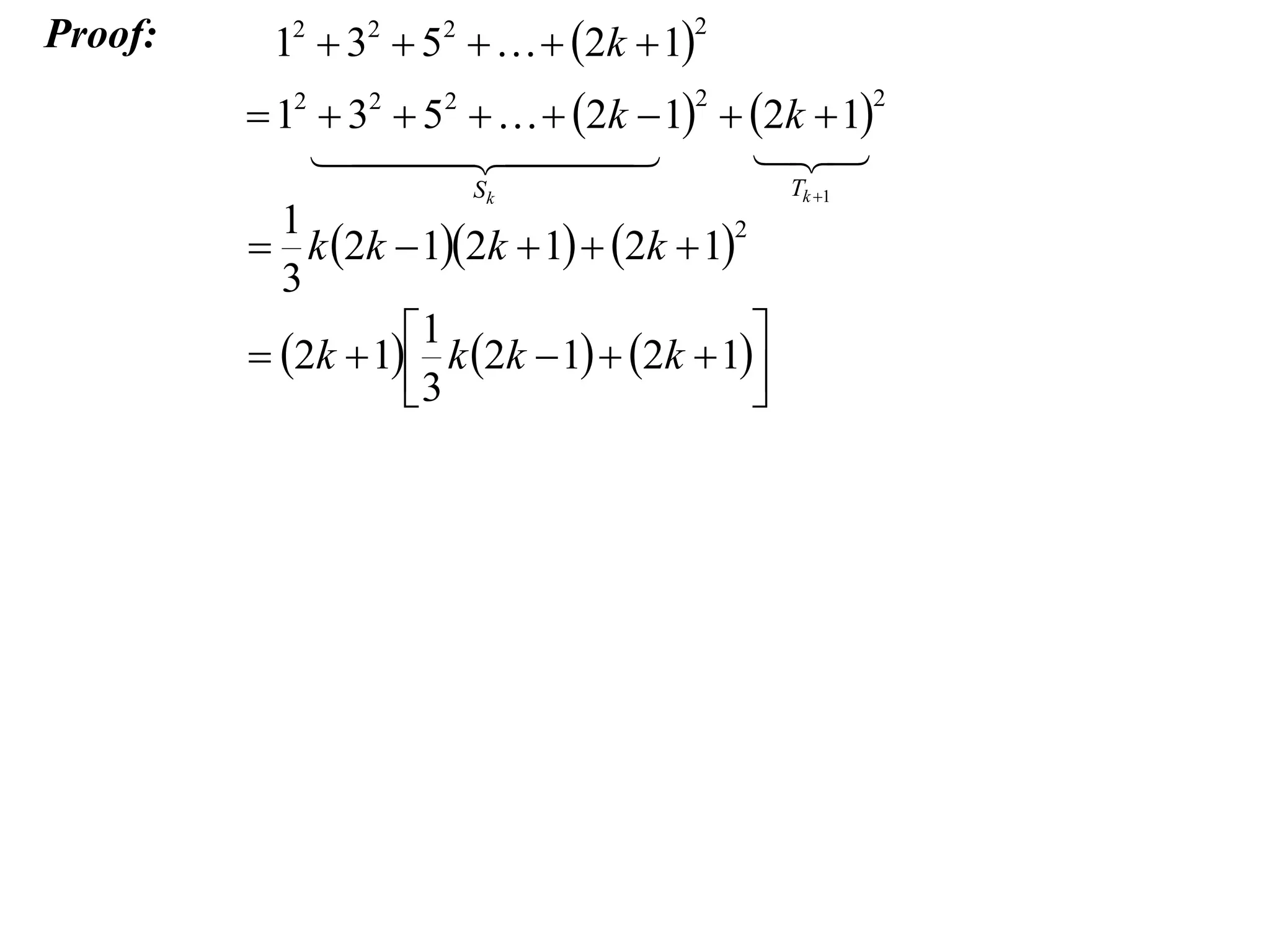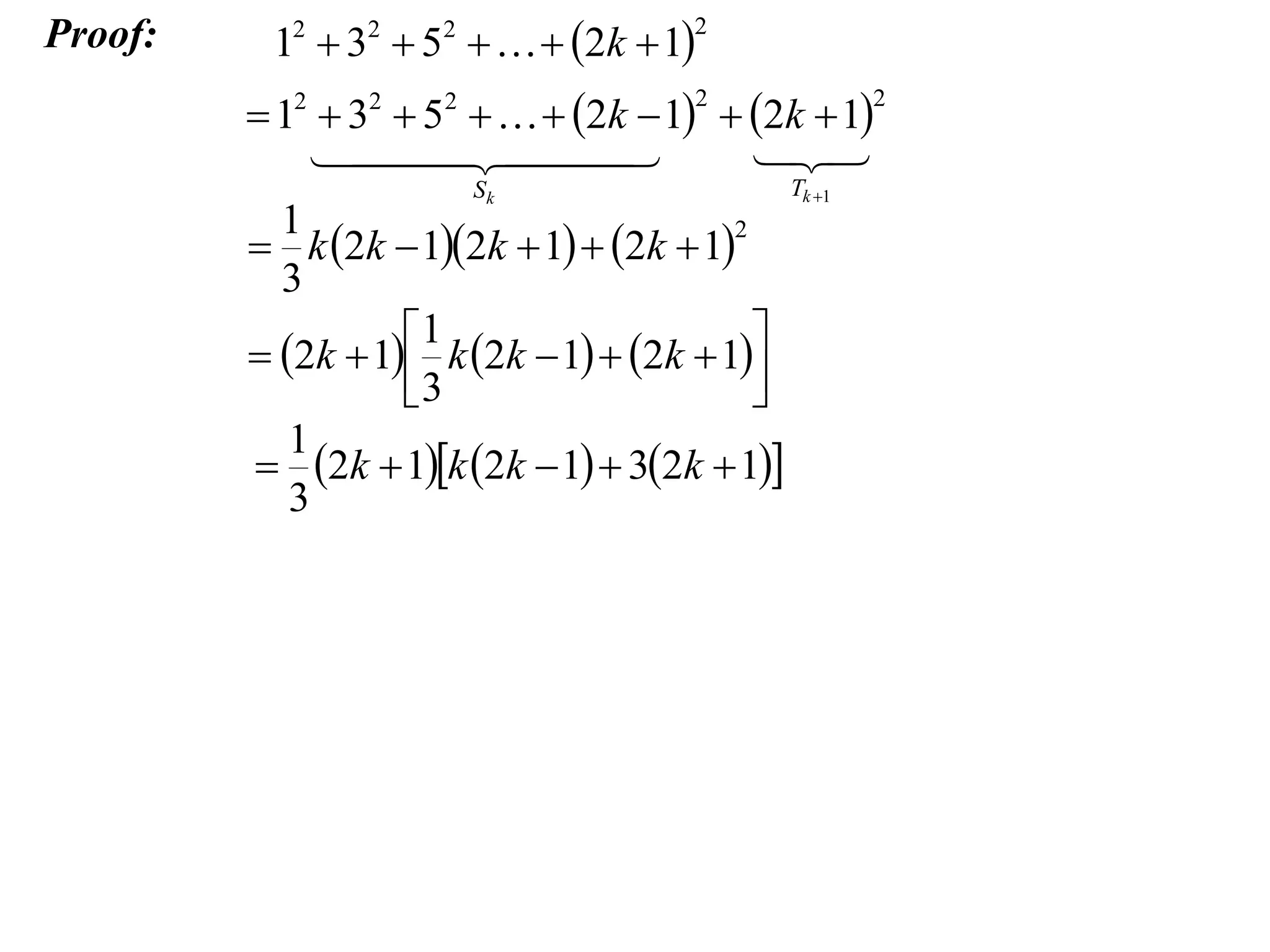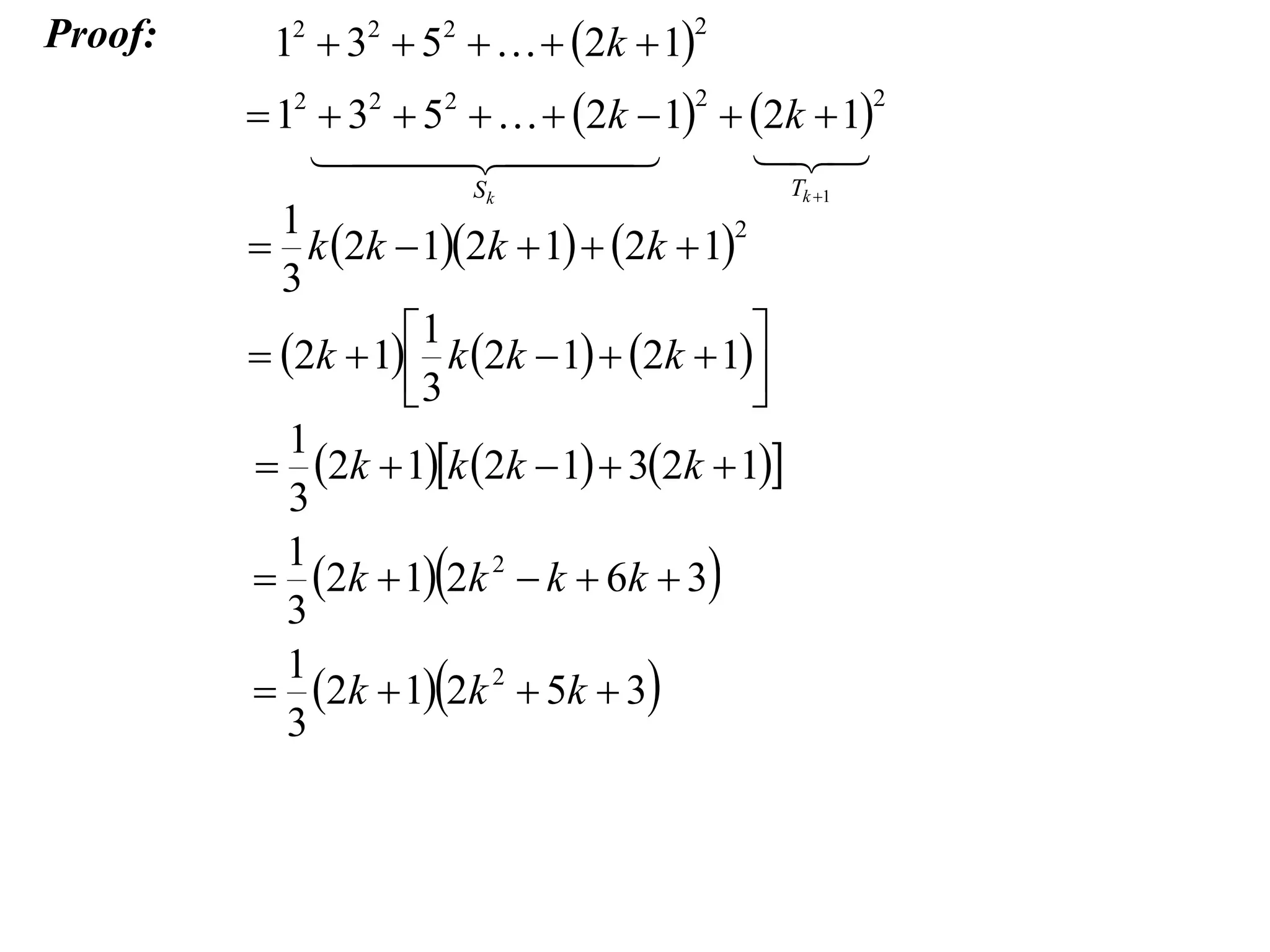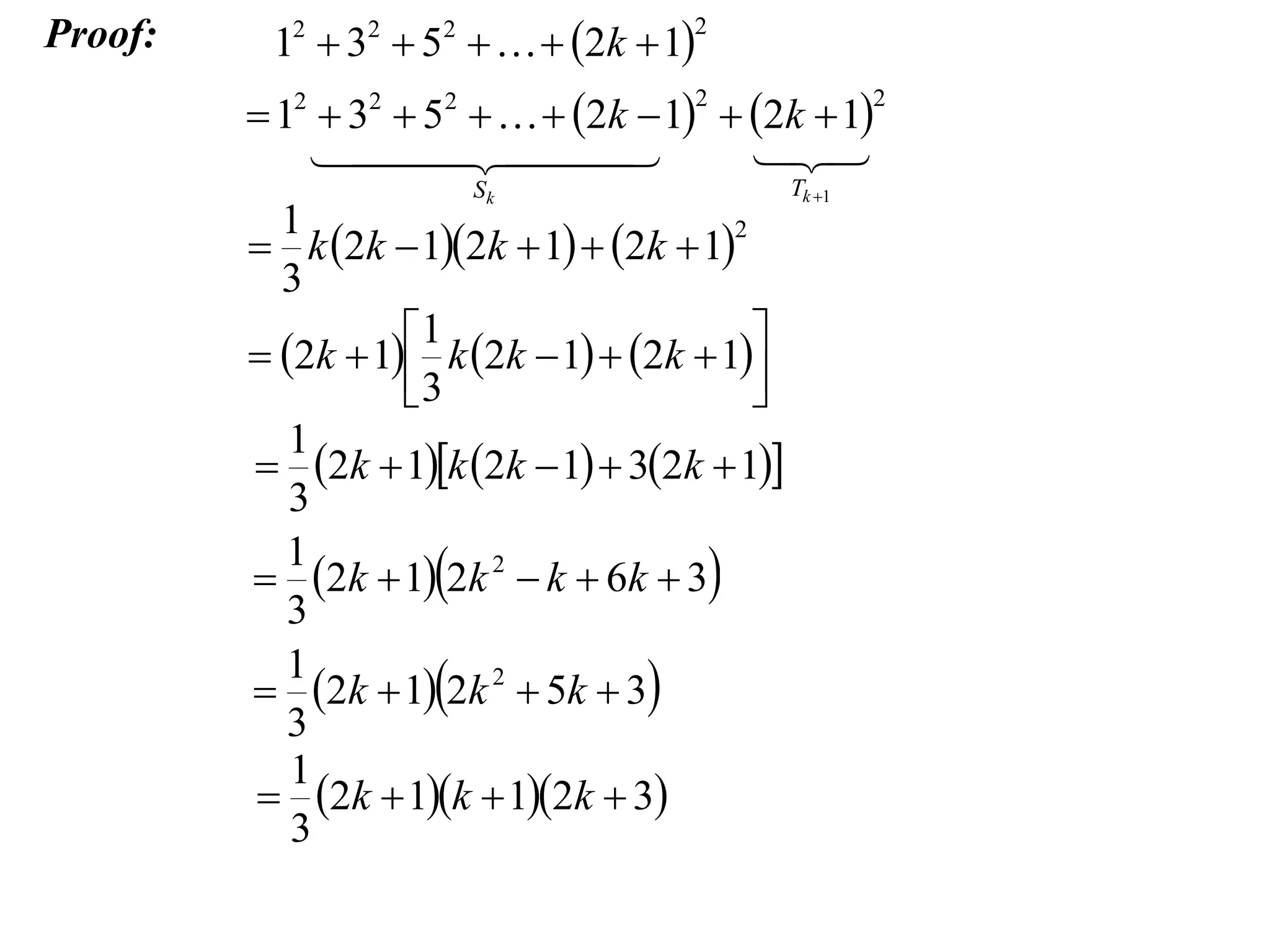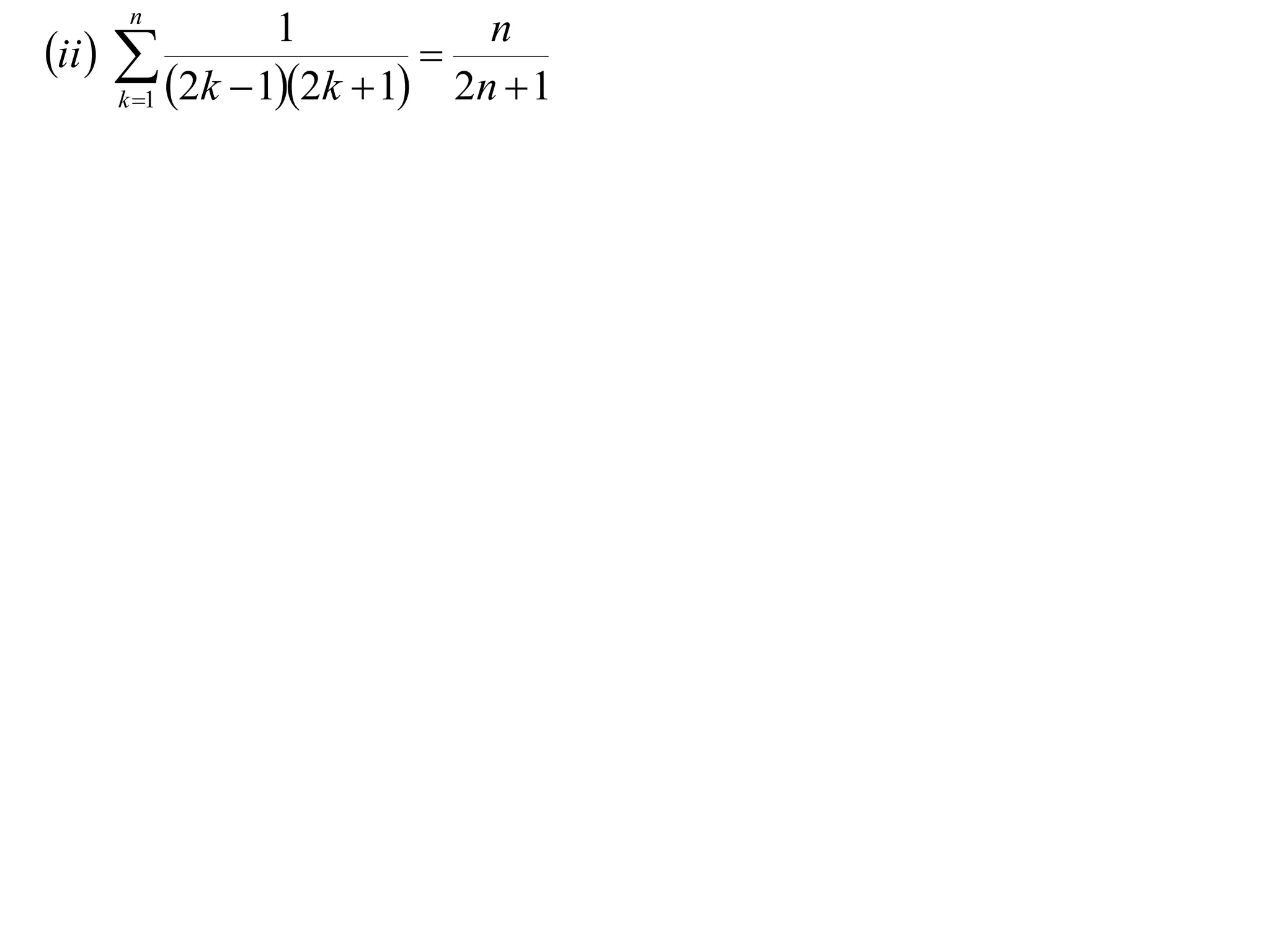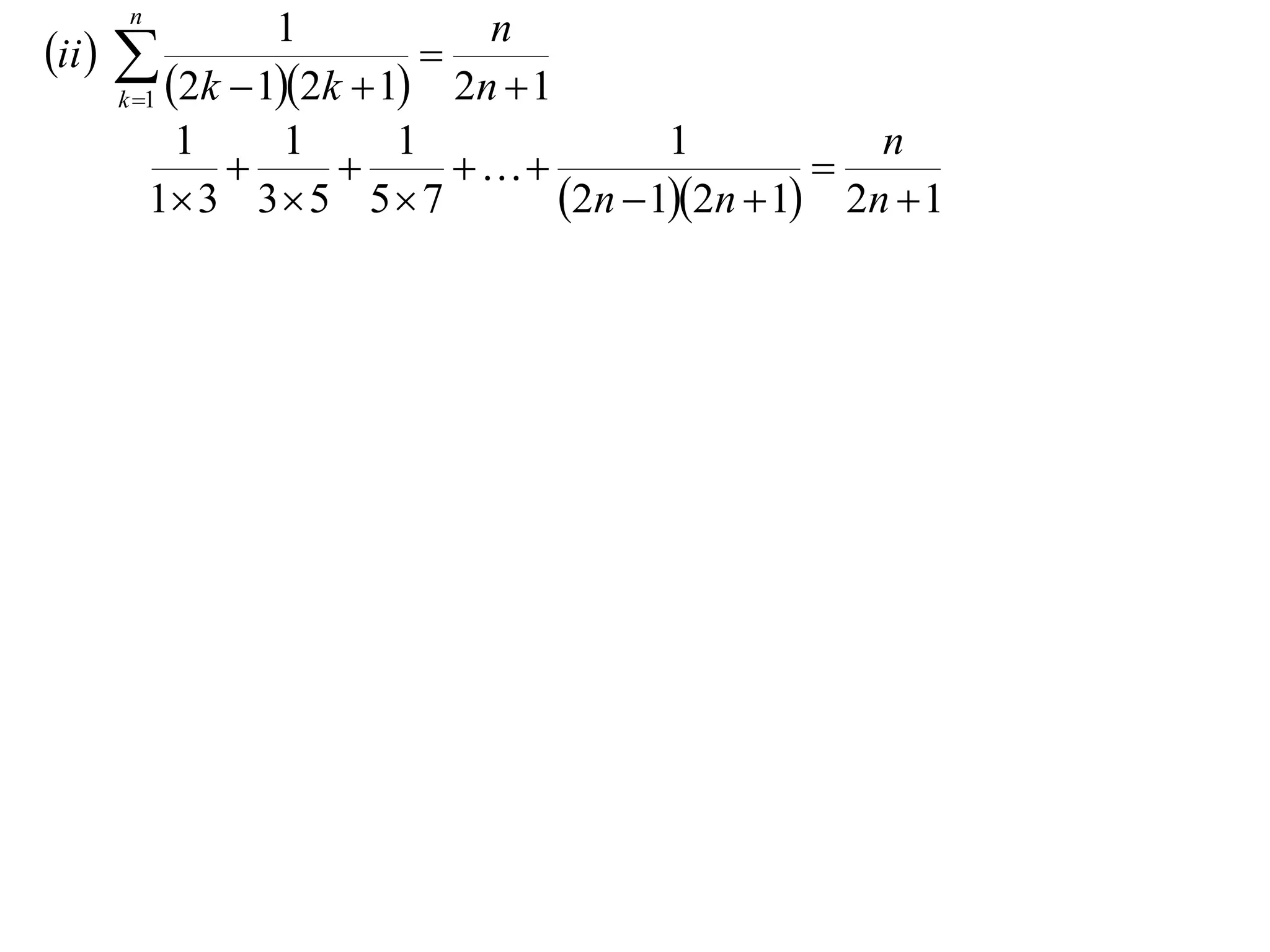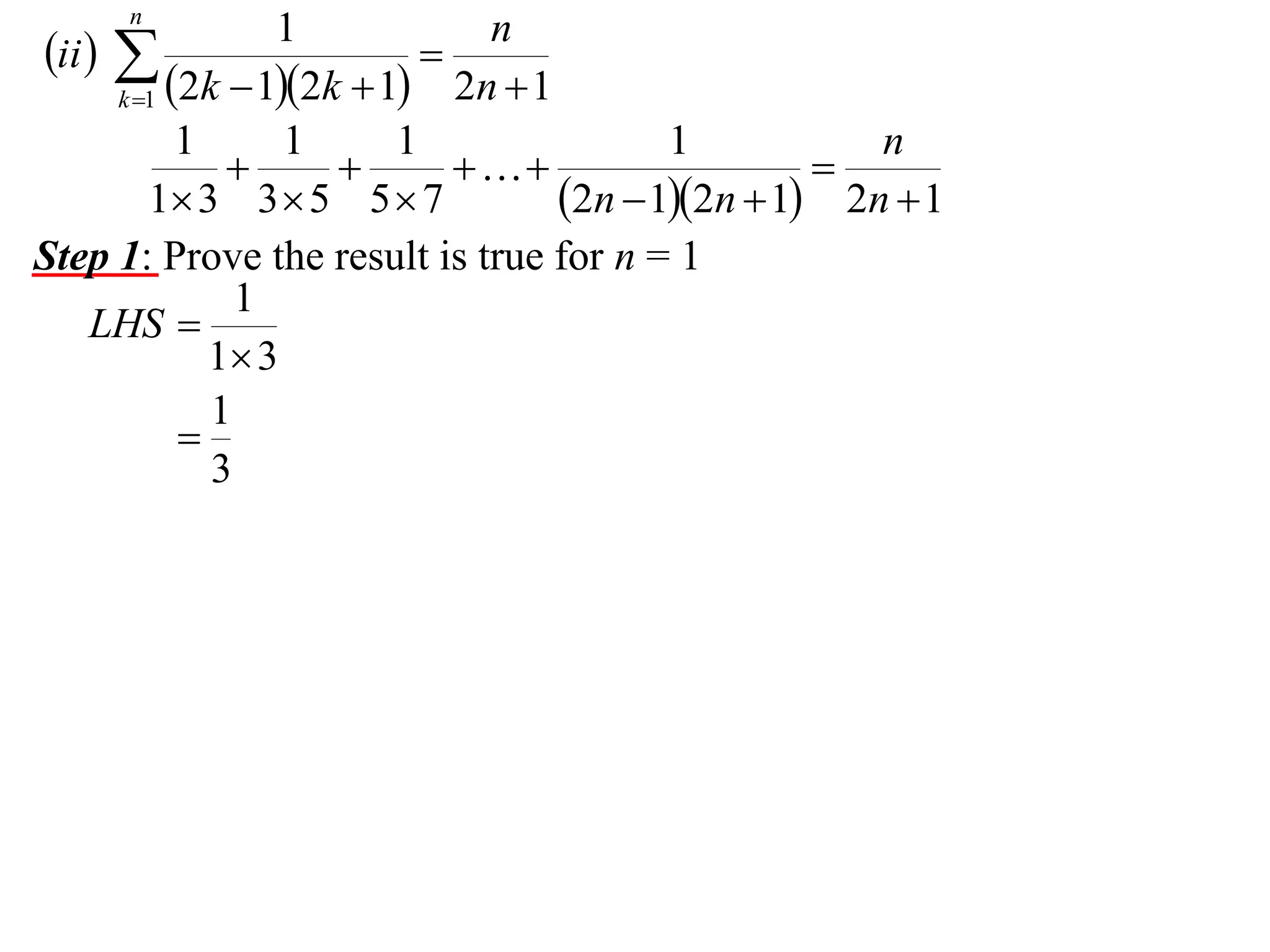The document describes the steps of mathematical induction. It includes: Step 1: Prove the result is true for the first term, usually n = 1. Step 2: Assume the result is true for an integer k. Step 3: Prove the result is true for k + 1, using the assumption from Step 2. Step 4: Conclude that since the result is true for n = 1 by Step 1, and true for n = k + 1 by Step 3, it is true for all positive integers n by induction. The example provided works through an induction proof for the sum of odd integers from 1 to 2n - 1.

1. Mathematical Induction

2. Mathematical Induction
Step 1: Prove the result is true for n = 1 (or whatever the first term
is)

3. Mathematical Induction
Step 1: Prove the result is true for n = 1 (or whatever the first term
is)
Step 2: Assume the result is true for n = k, where k is a positive
integer (or another condition that matches the question)

4. Mathematical Induction
Step 1: Prove the result is true for n = 1 (or whatever the first term
is)
Step 2: Assume the result is true for n = k, where k is a positive
integer (or another condition that matches the question)
Step 3: Prove the result is true for n = k + 1

5. Mathematical Induction
Step 1: Prove the result is true for n = 1 (or whatever the first term
is)
Step 2: Assume the result is true for n = k, where k is a positive
integer (or another condition that matches the question)
Step 3: Prove the result is true for n = k + 1
NOTE: It is important to note in your conclusion that the result is
true for n = k + 1 if it is true for n = k

6. Mathematical Induction
Step 1: Prove the result is true for n = 1 (or whatever the first term
is)
Step 2: Assume the result is true for n = k, where k is a positive
integer (or another condition that matches the question)
Step 3: Prove the result is true for n = k + 1
NOTE: It is important to note in your conclusion that the result is
true for n = k + 1 if it is true for n = k
Step 4: Since the result is true for n = 1, then the result is true for
all positive integral values of n by induction

7. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
2
2
2
2

8. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
2
2
2
2

9. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
2
2
LHS  12
1
2
2

10. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
1
LHS  12
RHS  12  12  1
3
1
1
 113
3
1
2
2
2
2

11. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
1
LHS  12
RHS  12  12  1
3
1
1
 113
3
1
 LHS  RHS
2
2
2
2

12. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
1
LHS  12
RHS  12  12  1
3
1
1
 113
3
1
 LHS  RHS
Hence the result is true for n = 1
2
2
2
2

13. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
1
LHS  12
RHS  12  12  1
3
1
1
 113
3
1
 LHS  RHS
Hence the result is true for n = 1
2
2
2
2
Step 2: Assume the result is true for n = k, where k is a positive
integer

14. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
1
LHS  12
RHS  12  12  1
3
1
1
 113
3
1
 LHS  RHS
Hence the result is true for n = 1
2
2
2
2
Step 2: Assume the result is true for n = k, where k is a positive
integer
1
2
i.e. 12  32  52    2k  1  k 2k  12k  1
3

15. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
1
LHS  12
RHS  12  12  1
3
1
1
 113
3
1
 LHS  RHS
Hence the result is true for n = 1
2
2
2
2
Step 2: Assume the result is true for n = k, where k is a positive
integer
1
2
i.e. 12  32  52    2k  1  k 2k  12k  1
3
Step 3: Prove the result is true for n = k + 1

16. 1
e.g.i  1  3  5    2n  1  n2n  12n  1
3
Step 1: Prove the result is true for n = 1
1
LHS  12
RHS  12  12  1
3
1
1
 113
3
1
 LHS  RHS
Hence the result is true for n = 1
2
2
2
2
Step 2: Assume the result is true for n = k, where k is a positive
integer
1
2
i.e. 12  32  52    2k  1  k 2k  12k  1
3
Step 3: Prove the result is true for n = k + 1
1
2
i.e. Prove : 12  32  52    2k  1  k  12k  12k  3
3

17. Proof:

18. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1
2
2

19. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1
 


2
Sk
2

20. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1

 


2
Sk
2
Tk 1

21. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1

 


2
Sk
1
2
 k 2k  12k  1  2k  1
3
2
Tk 1

22. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1

 


2
Sk
1
2
 k 2k  12k  1  2k  1
3
1

 2k  1 k 2k  1  2k  1
3

2
Tk 1

23. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1

 


2
Sk
1
2
 k 2k  12k  1  2k  1
3
1

 2k  1 k 2k  1  2k  1
3

1
 2k  1k 2k  1  32k  1
3
2
Tk 1

24. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1

 


2
Sk
1
2
 k 2k  12k  1  2k  1
3
1

 2k  1 k 2k  1  2k  1
3

1
 2k  1k 2k  1  32k  1
3
1
 2k  12k 2  k  6k  3
3
1
 2k  12k 2  5k  3
3
2
Tk 1

25. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1

 


2
Sk
1
2
 k 2k  12k  1  2k  1
3
1

 2k  1 k 2k  1  2k  1
3

1
 2k  1k 2k  1  32k  1
3
1
 2k  12k 2  k  6k  3
3
1
 2k  12k 2  5k  3
3
1
 2k  1k  12k  3
3
2
Tk 1

26. Proof:
12  32  52    2k  1
2
 12  32  52    2k  1  2k  1

 


2
Sk
2
Tk 1
1
2
 k 2k  12k  1  2k  1
3
1

 2k  1 k 2k  1  2k  1
3

1
 2k  1k 2k  1  32k  1
3
1
 2k  12k 2  k  6k  3
3
1
 2k  12k 2  5k  3
3
1
 2k  1k  12k  3
3
Hence the result is true for n = k + 1 if it is also true for n = k

27. Step 4: Since the result is true for n = 1, then the result is true for
all positive integral values of n by induction

28. n
1
n
ii  

2n  1
k 1 2k  12k  1

29. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1

30. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1
Step 1: Prove the result is true for n = 1

31. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1
Step 1: Prove the result is true for n = 1
1
LHS 
1 3
1

3

32. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1
Step 1: Prove the result is true for n = 1
1
1
LHS 
RHS 
1 3
2 1
1
1


3
3

33. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1
Step 1: Prove the result is true for n = 1
1
1
LHS 
RHS 
1 3
2 1
1
1


3
3
 LHS  RHS

34. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1
Step 1: Prove the result is true for n = 1
1
1
LHS 
RHS 
1 3
2 1
1
1


3
3
 LHS  RHS
Hence the result is true for n = 1

35. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1
Step 1: Prove the result is true for n = 1
1
1
LHS 
RHS 
1 3
2 1
1
1


3
3
 LHS  RHS
Hence the result is true for n = 1
Step 2: Assume the result is true for n = k, where k is a positive
integer

36. n
1
n
ii  

2n  1
k 1 2k  12k  1
1
1
1
1
n




1 3 3  5 5  7
2n  12n  1 2n  1
Step 1: Prove the result is true for n = 1
1
1
LHS 
RHS 
1 3
2 1
1
1


3
3
 LHS  RHS
Hence the result is true for n = 1
Step 2: Assume the result is true for n = k, where k is a positive
integer
1
1
1
1
k
i.e.




1 3 3  5 5  7
2k  12k  1 2k  1

37. Step 3: Prove the result is true for n = k + 1

38. Step 3: Prove the result is true for n = k + 1
1
1
1
1
k 1
i.e. Prove :




1 3 3  5 5  7
2k  12k  3 2k  3

39. Step 3: Prove the result is true for n = k + 1
1
1
1
1
k 1
i.e. Prove :




1 3 3  5 5  7
2k  12k  3 2k  3
Proof:

40. Step 3: Prove the result is true for n = k + 1
1
1
1
1
k 1
i.e. Prove :




1 3 3  5 5  7
2k  12k  3 2k  3
Proof:
1
1
1
1



1 3 3  5 5  7
2k  12k  3
1
1
1
1
1





1 3 3  5 5  7
2k  12k  1 2k  12k  3

41. Step 3: Prove the result is true for n = k + 1
1
1
1
1
k 1
i.e. Prove :




1 3 3  5 5  7
2k  12k  3 2k  3
Proof:
1
1
1
1



1 3 3  5 5  7
2k  12k  3
1
1
1
1
1





1 3 3  5 5  7
2k  12k  1 2k  12k  3
k
1


2k  1 2k  12k  3

42. Step 3: Prove the result is true for n = k + 1
1
1
1
1
k 1
i.e. Prove :




1 3 3  5 5  7
2k  12k  3 2k  3
Proof:
1
1
1
1



1 3 3  5 5  7
2k  12k  3
1
1
1
1
1





1 3 3  5 5  7
2k  12k  1 2k  12k  3
k
1


2k  1 2k  12k  3
k 2k  3  1

2k  12k  3

43. Step 3: Prove the result is true for n = k + 1
1
1
1
1
k 1
i.e. Prove :




1 3 3  5 5  7
2k  12k  3 2k  3
Proof:
1
1
1
1



1 3 3  5 5  7
2k  12k  3
1
1
1
1
1





1 3 3  5 5  7
2k  12k  1 2k  12k  3
k
1


2k  1 2k  12k  3
k 2k  3  1

2k  12k  3
2k 2  3k  1

2k  12k  3

44. Step 3: Prove the result is true for n = k + 1
1
1
1
1
k 1
i.e. Prove :




1 3 3  5 5  7
2k  12k  3 2k  3
Proof:
1
1
1
1



1 3 3  5 5  7
2k  12k  3
1
1
1
1
1





1 3 3  5 5  7
2k  12k  1 2k  12k  3
k
1


2k  1 2k  12k  3
k 2k  3  1

2k  12k  3
2k 2  3k  1

2k  12k  3
2k  1k  1

2k  12k  3

45. 
k  1
2k  3

46. 
k  1
2k  3
Hence the result is true for n = k + 1 if it is also true for n = k

47. 
k  1
2k  3
Hence the result is true for n = k + 1 if it is also true for n = k
Step 4: Since the result is true for n = 1, then the result is true for
all positive integral values of n by induction

48. 
k  1
2k  3
Hence the result is true for n = k + 1 if it is also true for n = k
Step 4: Since the result is true for n = 1, then the result is true for
all positive integral values of n by induction
Exercise 6N; 1 ace etc, 10(polygon), 13