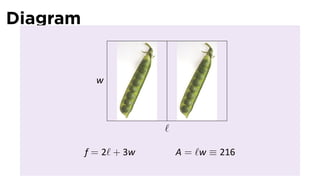
This document contains lecture notes from a Calculus I class discussing optimization problems. It begins with announcements about upcoming exams and courses the professor is teaching. It then presents an example problem about finding the rectangle of a fixed perimeter with the maximum area. The solution uses calculus techniques like taking the derivative to find the critical points and determine that the optimal rectangle is a square. The notes discuss strategies for solving optimization problems and summarize the key steps to take.










![Solution
Solu on (Con nued)
p − 2w
Since p = 2ℓ + 2w, we have ℓ = , so
2
p − 2w 1 1
A = ℓw = · w = (p − 2w)(w) = pw − w2
2 2 2
Now we have A as a func on of w alone (p is constant).
The natural domain of this func on is [0, p/2] (we want to
make sure A(w) ≥ 0).](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-13-320.jpg)
![Solution
Solu on (Con nued)
1
We use the Closed Interval Method for A(w) = pw − w2 on
2
[0, p/2].](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-14-320.jpg)
![Solution
Solu on (Con nued)
1
We use the Closed Interval Method for A(w) = pw − w2 on
2
[0, p/2].
At the endpoints, A(0) = A(p/2) = 0.](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-15-320.jpg)
![Solution
Solu on (Con nued)
1
We use the Closed Interval Method for A(w) = pw − w2 on
2
[0, p/2].
At the endpoints, A(0) = A(p/2) = 0.
dA 1
To find the cri cal points, we find = p − 2w.
dw 2](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-16-320.jpg)











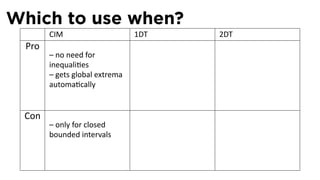
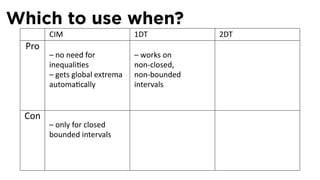
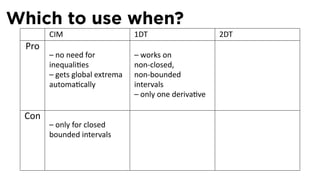
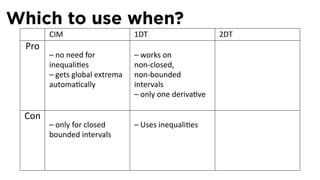
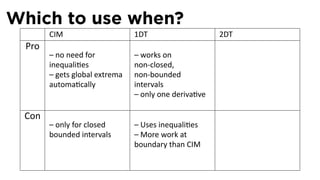
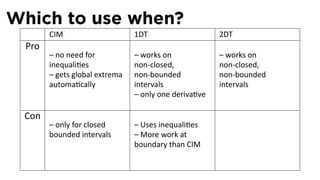
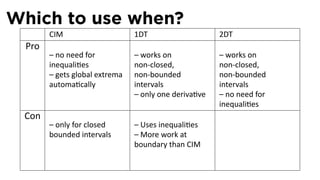
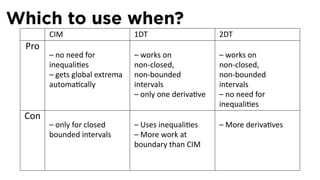
![The Closed Interval Method
See Section 4.1
The Closed Interval Method
To find the extreme values of a func on f on [a, b], we need to:
Evaluate f at the endpoints a and b
Evaluate f at the cri cal points x where either f′ (x) = 0 or f is
not differen able at x.
The points with the largest func on value are the global
maximum points
The points with the smallest/most nega ve func on value are
the global minimum points.](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-29-320.jpg)


![Recall: The Second Derivative Test
See Section 4.3
Theorem (The Second Deriva ve Test)
Let f, f′ , and f′′ be con nuous on [a, b]. Let c be in (a, b) with
f′ (c) = 0.
If f′′ (c) < 0, then f(c) is a local maximum.
If f′′ (c) > 0, then f(c) is a local minimum.](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-32-320.jpg)
![Recall: The Second Derivative Test
See Section 4.3
Theorem (The Second Deriva ve Test)
Let f, f′ , and f′′ be con nuous on [a, b]. Let c be in (a, b) with
f′ (c) = 0.
If f′′ (c) < 0, then f(c) is a local maximum.
If f′′ (c) > 0, then f(c) is a local minimum.
Warning
If f′′ (c) = 0, the second deriva ve test is inconclusive (this does not
mean c is neither; we just don’t know yet).](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-33-320.jpg)




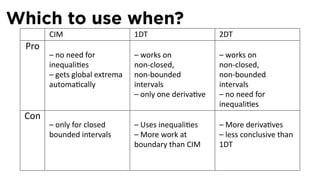








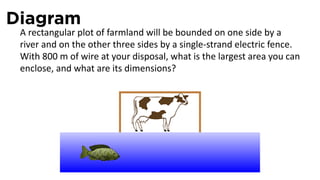


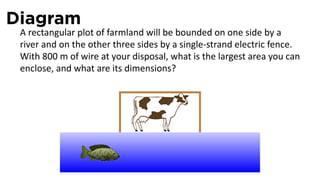
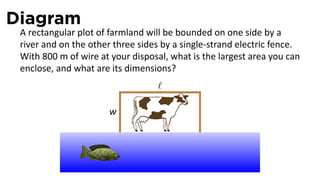


![Solution
Solu on
4. Q = area = ℓw.
5. Since p = ℓ + 2w, we have ℓ = p − 2w and so
Q(w) = (p − 2w)(w) = pw − 2w2
The domain of Q is [0, p/2]](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-63-320.jpg)
![Solution
Solu on
4. Q = area = ℓw.
5. Since p = ℓ + 2w, we have ℓ = p − 2w and so
Q(w) = (p − 2w)(w) = pw − 2w2
The domain of Q is [0, p/2]
dQ p
6. = p − 4w, which is zero when w = .
dw 4](https://image.slidesharecdn.com/lesson22-optimization011slides-110419070004-phpapp02/85/Lesson-22-Optimization-Problems-slides-64-320.jpg)