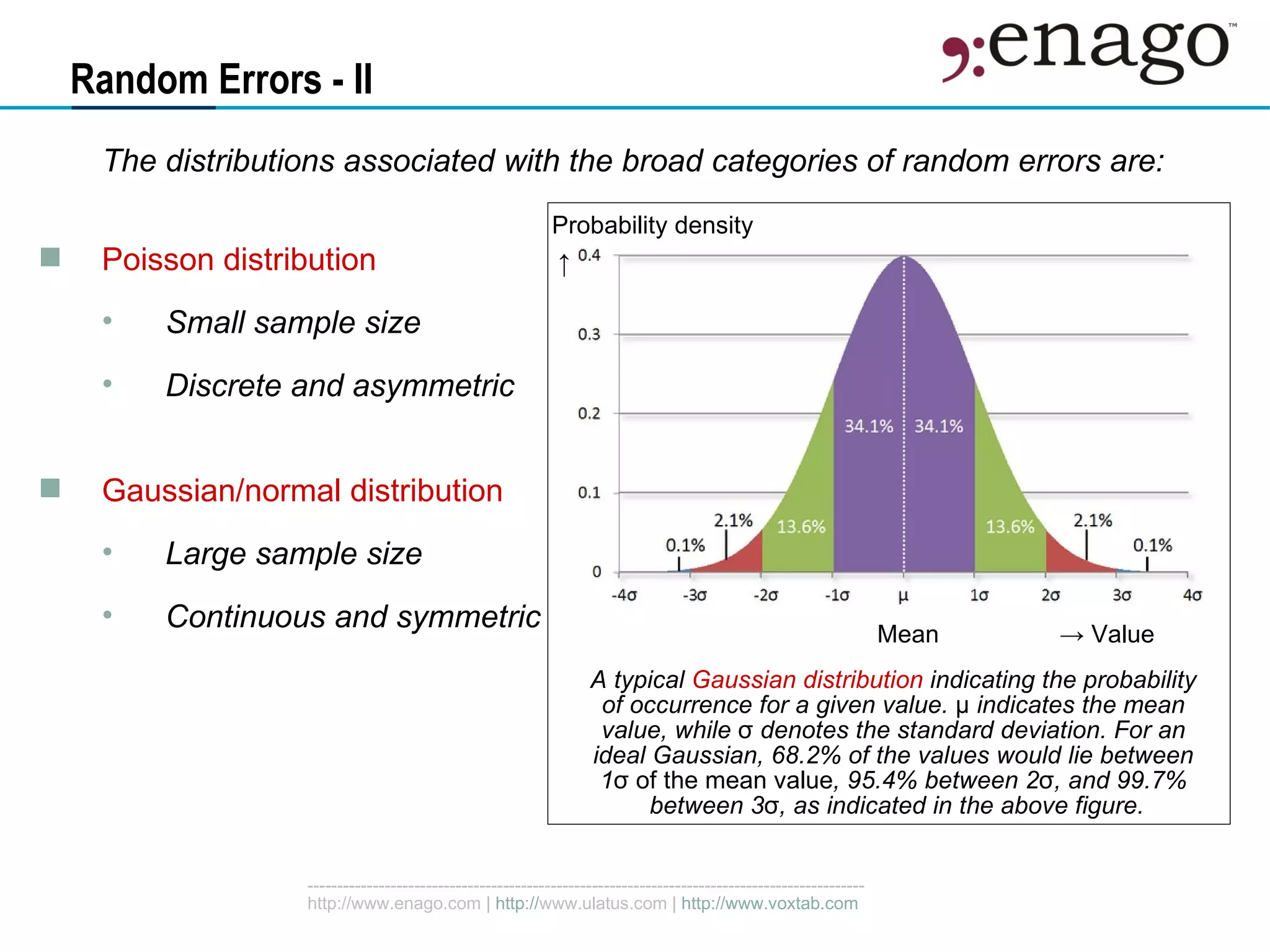
This document discusses sources of error in numerical results, including random errors and systematic errors. Random errors are due to statistical fluctuations and can be characterized by probability distributions like Gaussian. Systematic errors bias results in a predetermined way and are reduced by examining measurement methods. Propagation of errors must account for all sources of random and systematic error to obtain accurate results with appropriate error ranges.

1. Accuracy of Numerical Results Random and Systematic Errors October 2010

2. Introduction Random Errors Systematic Errors Propagation of Errors Accuracy of Numerical Results

3. Introduction Numerical results or analyses are an integral aspect of most research papers. To ensure accuracy , and therefore reliability and integrity of the results: Take into account experimental conditions or the method of data collection Determine sources of error (random or systematic) Errors are inherent to all data, and are distinct from mistakes or blunders !! Examine and include contribution to errors from all sources Assign appropriate errors to measured or derived quantities

4. Introduction Random Errors Systematic Errors Propagation of Errors Accuracy of Numerical Results

5. Random Errors - I Simultaneous measurements of the same quantity: values distributed accordingly to the probability of occurrence (probability distribution) Sources of random errors Statistical effects Limitations in the measurement process Common probability distributions Different forms of binomial distribution (low probability of occurrence/success) Small number of measurements or sample size ( Poisson ) Large number of measurements or sample size ( Gaussian )

6. Random Errors - II The distributions associated with the broad categories of random errors are: Poisson distribution Small sample size Discrete and asymmetric Gaussian/normal distribution Large sample size Continuous and symmetric -> Value Probability density -> Mean A typical Gaussian distribution indicating the probability of occurrence for a given value. μ indicates the mean value, while σ denotes the standard deviation. For an ideal Gaussian, 68.2% of the values would lie between 1 σ of the mean value , 95.4% between 2 σ , and 99.7% between 3 σ , as indicated in the above figure.

7. Introduction Random Errors Systematic Errors Propagation of Errors Accuracy of Numerical Results

8. Systematic Errors - I Systematic errors tend to bias measured values in a pre-determined manner Possible sources of systematic errors Imperfections in the measuring equipment Incorrect use of apparatus or implementation of techniques Isolating/reducing systematic errors Examine and analyze measurement apparatus and techniques Careful practices in the implementation of research

9. Systematic Errors - II Similar experiments performed at different laboratories with varying conditions and equipment have unique associated systematic errors If two different experiments report results about the same quantity which are variance with each other, this may be due to incorrect or incomplete treatment of systematic errors in one or both. Systematic errors lead to a difference in the actual and measured values. In this simple example, the error can be characterized in terms of a difference in the offset (values at zero) and slope of the two lines.

10. Introduction Random Errors Systematic Errors Propagation of Errors Accuracy of Numerical Results

11. Propagation of Errors Isolate and quantify all sources of random and systematic errors Combine all sources of error: cumulative error on the measured quantity Different procedure based on whether measured quantities are dependent or independent of each other Reliability of quoted values depends on rigorous and thorough error analysis Accurate values , with appropriate error bars , ensure sound results , which are respected by peers

12. About Crimson Enago ™ is the leading editing and publication service provider for scientific manuscripts in Japan, and has a total of over 10000 clients in many countries. Ulatus™ provides Japanese to English translation services in numerous subject areas for almost every document type. Voxtab™ is the transcription arm of our business and provides accurate and reliable transcriptions, with fast turnaround times. 英文编辑 · 英文校对 http:// www.enago.cn / 英文編修‧論文修改 http:// www.enago.tw / 英語テープ起こしボックスブ http:// www.voxtab.jp / 日英・英日翻訳ユレイタス http:// www.ulatus.jp / 英文校正エナゴ http:// www.enago.jp / English Transcription Services http:// www.voxtab.com / English Translation Services http:// www.ulatus.com / English Editing Services http:// www.enago.com /