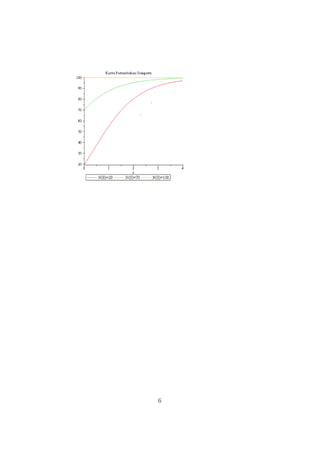
Dokumen ini menjelaskan model pertumbuhan Gompertz yang digunakan untuk mempelajari populasi, termasuk persamaan matematis dan analisis asimtot. Penulis menunjukkan bagaimana kurva pertumbuhan berperilaku tergantung pada nilai awal n0 dibandingkan dengan konstanta k. Selain itu, terdapat diskusi mengenai titik belok kurva dan bagaimana kurva bereaksi terhadap perubahan nilai awal populasi.

1. Tugas Kalkulus Model Pertumbuhan
Gompertz
Dadang Amir Hamzah
May 10, 2013
Kurva pertumbuhan Gompertz digunakan untuk mempelajari pertum-
buhan populasi. Kurva dari model ini mempunyai sifat yang serupa dengan
kurva model pertumbuhan logistik. Kurva pertumbuhan Gompertz dinyata-
kan dengan
N(t) = K exp(ae−bt
),
dengan t ≥ 0, dan K, b adalah konstanta-konstanta positif.
a. Tunjukkan bahwa N(0) = Ke−a
dan apabila N0 = N(0) maka a =
ln K
N0
.
Jawab:
Diketahui kurva pertumbuhan Gompertz adalah
N(t) = K exp(−ae−bt
), (1)
untuk t ≥ 0, dan K, b konstanta positif. N(0) terjadi ketika t = 0, de-
ngan mensubstitusi t = 0 ke persamaan (1) didapat N(0) = K exp(−a).
Kemudian dengan menuliskan N(0) = N0 dan dengan menggunakan
sifat eksponen didapat
a = ln
K
N0
.
1

2. b. Tunjukkan bahwa y = K adalah asimtot datar. Kemudian tunjukkan
pula bahwa jika N0 < K maka N(t) < K, Jika N0 = K maka N(t) =
K, dan jika N0 > K maka N(t) > K.
Jawab:
Akan ditunjukkan bahwa garis y = K adalah asimtot datar dari Kurva
N(t), artinya harus ditunjukkan bahwa
lim
t→∞
N(t) = K.
Perhatikan bahwa N(t) = K exp(−ae−bt
). Apabila kita limitkan untuk
t → ∞ akan didapat
limt→∞ K exp(−ae−bt
= K exp(−ae∞
)
= K exp(0)
= K.
Jadi terbukti bahwa garis y = K adalah asimtot datar dari kurva N(t).
Selanjutnya akan ditunjukkan jika N0 < K maka Nt < K. Karena
K > 0 maka N0 > 0, akibatnya
N0 < K dengan mengambil ln dikedua ruas
ln N0 < ln K
ln K − ln N0 > 0
ln K
N0
> 0, (Karena a = ln K
N0
)
a > 0, (kalikan kedua ruas dengan − e−bt
)
−ae−bt
< 1, (eksponenkan kedua ruas kemudian kalikan dengan K)
K exp(−ae−bt
) < K
N(t) < K.
Jadi terbukti bahwa jika N0 < K maka Nt < K. Dengan cara yang
sama dapat juga ditunjukkan bahwa jika N0 = K maka Nt = K, dan
2

3. jika N0 > K maka Nt > K.
(Catatan: Hati-hati dengan tanda ” > ” dan ” < ”)
c. Tunjukkan bahwa
dN
dt
= bN (ln K − ln N) dan
d2
N
dt
= b
dN
dt
(ln K − ln N − 1).
Jawab:
Perhatikan bahwa
N(t) = K exp(−ae−bt
) , (dengan menurunkan kedua ruas terhadap t)
dN
dt
= ab e−by
K exp(−ae−bt
)
= ab e−by
N
= bN ae−by
= bN (ln K − ln N).
Jadi terbukti bahwa dN
dt
= bN (ln K − ln N).
Untuk mendapatkan d2N
dt
turunkan dN
dt
terhadap t sehigga
d2N
dt
= b dN
dt
(ln K − ln N) + bN(0 − 1
N
dN
dt
)
= b dN
dt
(ln K − ln N − 1).
Jadi terbukti bahwa d2N
dt
= b dN
dt
(ln K − ln N − 1).
d. Gunakan hasil pada b dan c untuk menunjukkan jika N0 < K maka
N(t) naik sempurna dan jika N0 > K maka N(t) turun sempurna.
Jawab:
Kurva N(t) naik jika dN
dt
> 0. Akan ditunjukkan bahwa jika N0 < K
maka dN
dt
> 0.
Pada soal bagian b telah ditunjukkan bahwa jika N0 < K maka N < K.
3

4. Selanjutnya perhatikan bahwa untuk N < K berlaku
ln N < ln K
ln K − ln N > 0, (tambahkan kedua ruas dengan − ln N)
bN (ln K − ln N) > 0, (kalikan kedua ruas dengan bN)
dN
dt
> 0.
Jadi terbukti bahwa jika N0 < K maka N(t) naik sempurna. Dengan
cara yang sama perhatikan bahwa
N > K
ln N > ln K
ln K − ln N < 0
bN (ln K − ln N) < 0
dN
dt
< 0.
Jadi terbukti bahwa jika N0 > K maka N(t) turun sempurna.
e. Saat t berapakah kurva N(t) melalui titik belok? Diskusikan kecekun-
gan dan kecembungannya?
Jawab :
Dengan menggunakan uji turunan kedua titik belok kurva N(t) dicapai
di t yang memenuhi d2N
dt
= 0, kemudian kurva N(t) cekung keatas jika
d2N
dt
> 0 dan kurva N(t) cekung kebawah jika d2N
dt
< 0.
Dari soal c diketahui d2N
dt
= b dN
dt
(ln K − ln N − 1).
Titik belok dicapai di t yang memenuhi
d2
N
dt
= b
dN
dt
(ln K − ln N − 1) = 0
Hal ini mungkin terjadi hanya untuk
ln K − ln N − 1 = 0
4

5. yakni
ln N + 1 = ln K
ln K − ae−bt
+ 1 = ln K
−ae−bt
+ 1 = 0
1 = ae−bt
ebt
= a
ln a = bt
t = ln a
b
.
Jadi titik belok dari N(t) terjadi saat t = ln a
b
.
Kemudian dengan cara yang sama d2N
dt2 > 0 dicapai saat t < ln a
b
dan d2N
dt2
dicapai saat t > ln a
b
. Artinya kurva N(t) terbuka keatas saat t < ln a
b
kemudian belok saat t = ln a
b
dan terbuka kebawah saat t > ln a
b
.
e. Gambarkan kurva N(t) untuk K = 100 , b = 1 dan kondisi-kondisi
berikut:
i. N0 = 20.
ii. N0 = 70.
iii. N0 = 150.
jawab:
5

6. 6