1. Rでコンジョイント分析
Tokyo.R #30
@bob3bob3

2. コンジョイント分析とは？
• マーケティングリサーチで使われる手法
の一つ。
• 消費者が商品やサービスのどんな要素を
重視しているのかを探るための方法。
• 商品やサービスを要素に分解し、それを
様々に組み合わせたものを消費者に評価
させ、どんな組み合わせにするとどんな
評価が得られるのかを推定する。

3. なぜコンジョイント分析を使うの
か？
• 消費者自身は、自分がどんな要素がどれくらい
重視しているのかに自覚的ではないことが多い。
• だから、個別の要素についての直接的に重要度
を尋ねることはあまり有効とは言えない。
• また個々の要素同士がトレードオフの関係にあ
ることもしばしば。
• だから、全体の組み合わせとして評価を測定し、
分析をする。

4. 商品を要素に分解するとは？
•本格デジカメの構成要素
– レンズ 〔交換式／固定〕
– ミラー 〔一眼レフ／ミラーレス〕
– 本体の色 〔黒／黄色〕
– センサーサイズ 〔APS-C／マイクロフォーサーズ〕
– HDR機能 〔有り／無し〕
– 電子水準器 〔有り／無し〕
– 動画撮影 〔有り／無し〕
– WiFi 〔有／無〕
•８属性、各２水準

5. 要素の組み合わせを考えると？
•８属性、各２水準の全組み合わせは、２
の８乗＝256通り。
•全組み合わせについて評価してもらえば、
最も購買意欲を高める組み合わせは自ず
とわかる。
•が、現実的ではない。

6. そこで直交計画
• 実験計画法の世界で生まれた
実験の回数を少なくするテク
ニック。
– 直交表と呼ばれる「どの属性
でも全ての要素が同じ数だけ
出現する、すべて異なる組み
合わせの表」を使う。
– 直交表は各列間の相関係数が
ゼロになる。
– L8直交表なら全組み合わせで
128通りの実験が必要なとこ
ろが８通りの実験で済む（交
互作用を考えない場合）。
– それでも実験数が減らせない
場合、直交性を妥協して実験
数を減らす場合もある。
実験
番号
属性
A B C D E F G
1 1 1 1 1 1 1 1
2 1 1 1 2 2 2 2
3 1 2 2 1 1 2 2
4 1 2 2 2 2 1 1
5 2 1 2 1 2 1 2
6 2 1 2 2 1 2 1
7 2 2 1 1 2 2 1
8 2 2 1 2 1 1 2
※直交表の例：L8(27)直交表
詳しくは第22回Tokyo.Rでの @itoyan さん
の発表資料を参照してください。
「Rで実験計画法（後編）」
http://www.slideshare.net/itoyan110/r-
14261638

7. 質問形式
•直交表を使って作った組み合わせについて消費
者の評価を得るにはいくつかの質問形式がある。
– 順位づけ「１位からｎ位まで順位を付けてくださ
い」
– 評定値：「10点満点で点数を付けてください」
– 恒常和法「持ち点100点を振り分けてください」
– 選択法「（複数の組み合わせを呈示して）一つ選ん
でください」
– などなど

8. 測定結果を分析する
• 質問形式によってその後の分析方法が異
なる。
– 順位づけ：順序ロジットモデル
– 評定値：重回帰分析
– 恒常和法：ロジスティック回帰モデル
– 選択法：条件付きロジットモデル
– 一対比較法

9. 結果の解釈と使い方
• 効用値は各水準が、重要度は各属性が全体評価に対してどの程度影響する
かを示す。
– これにより、どんな組み合わせがどんな評価を得るか推定することができる。
– また、回答者の属性（性別、年齢など）別に分析することで、ターゲットごと
にどんな商品が高い評価を得そうかを推定できる。
– さらに、個人別に分析を行い、その結果に基づいてクラスタリングを行い、重
視する属性の違いに基づくセグメンテーションなども可能（ベネフィットセグ
メンテーション）。

10. 本題

11. Rでコンジョイント分析
•直交表はDoE.baseパッケージ、AlgDesign
パッケージで作成可能。
•分析は
– 順序ロジットモデル：{MASS}polr()
– 重回帰：lm()
– ロジスティック回帰：glm()
– 条件付きロジット：{survival}clogit()
•最近出たconjointパッケージを使うのが便利。
– caFactorialDesign()で組み合わせ作成。
– Conjoint()で分析。
•ワルシャワの人が作ったらしい。なので一部がポーランド語
になってる。

12. 組み合わせ作成
install.packages("conjoint") #パッケージのインストール。初回のみ。
library(conjoint) #パッケージの呼び出し。
# 属性と水準の指定
experiment <- expand.grid(
レンズ = c("交換式", "固定"),
ミラー = c("一眼レフ", "ミラーレス"),
本体の色 = c("黒", "黄色"),
センサーサイズ = c("APS-C", "マイクロフォーサーズ"),
HDR機能 = c("無し", "有り"),
電子水準器 = c("無し", "有り"),
動画撮影 = c("無し", "有り"),
WiFi = c("無し", "有り"))

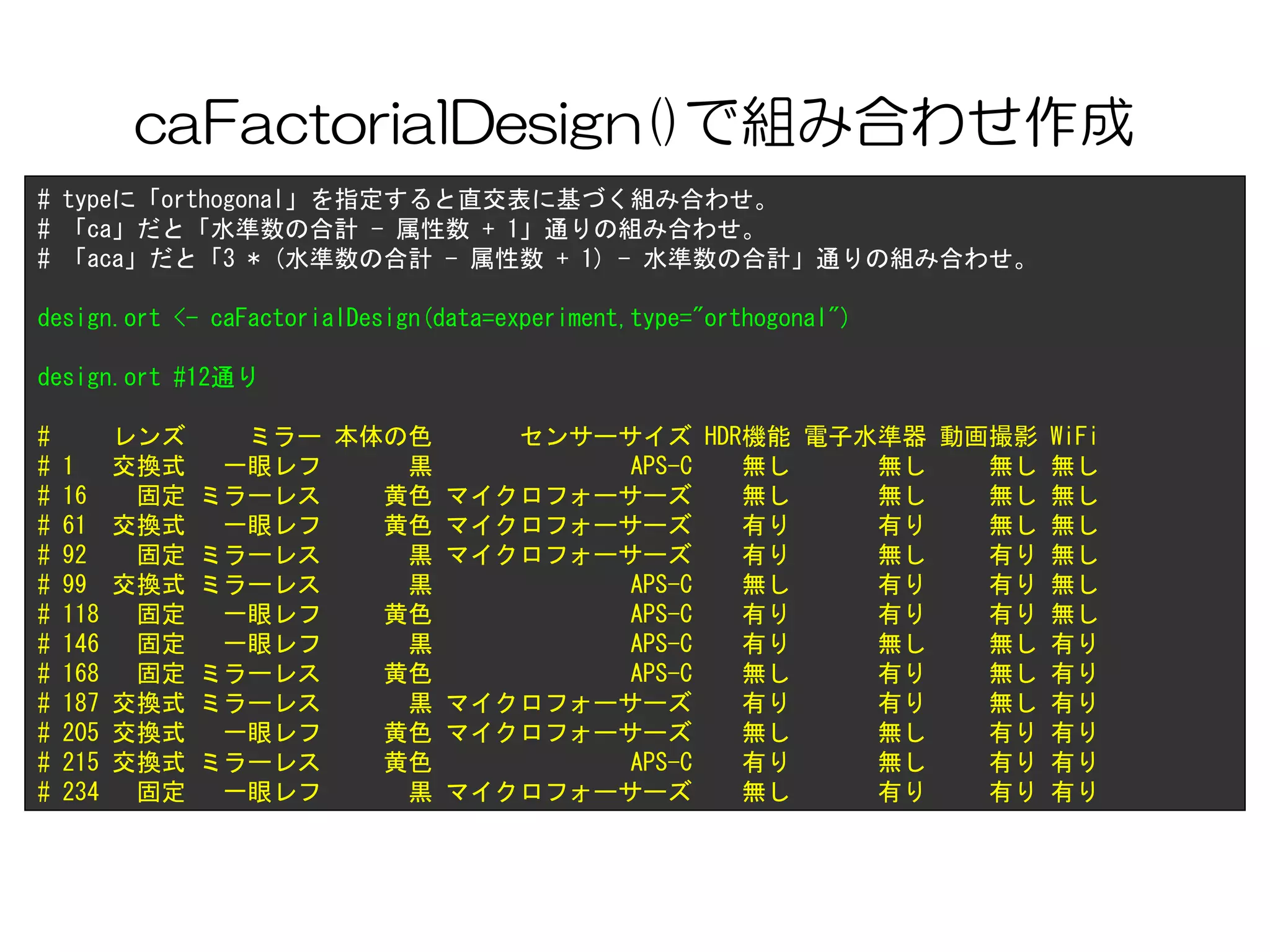
13. caFactorialDesign()で組み合わせ作成
# typeに「orthogonal」を指定すると直交表に基づく組み合わせ。
# 「ca」だと「水準数の合計 - 属性数 + 1」通りの組み合わせ。
# 「aca」だと「3 * (水準数の合計 - 属性数 + 1) - 水準数の合計」通りの組み合わせ。
design.ort <- caFactorialDesign(data=experiment,type="orthogonal")
design.ort #12通り
# レンズ ミラー 本体の色 センサーサイズ HDR機能 電子水準器 動画撮影 WiFi
# 1 交換式 一眼レフ 黒 APS-C 無し 無し 無し 無し
# 16 固定 ミラーレス 黄色 マイクロフォーサーズ 無し 無し 無し 無し
# 61 交換式 一眼レフ 黄色 マイクロフォーサーズ 有り 有り 無し 無し
# 92 固定 ミラーレス 黒 マイクロフォーサーズ 有り 無し 有り 無し
# 99 交換式 ミラーレス 黒 APS-C 無し 有り 有り 無し
# 118 固定 一眼レフ 黄色 APS-C 有り 有り 有り 無し
# 146 固定 一眼レフ 黒 APS-C 有り 無し 無し 有り
# 168 固定 ミラーレス 黄色 APS-C 無し 有り 無し 有り
# 187 交換式 ミラーレス 黒 マイクロフォーサーズ 有り 有り 無し 有り
# 205 交換式 一眼レフ 黄色 マイクロフォーサーズ 無し 無し 有り 有り
# 215 交換式 ミラーレス 黄色 APS-C 有り 無し 有り 有り
# 234 固定 一眼レフ 黒 マイクロフォーサーズ 無し 有り 有り 有り

14. 直交性の確認
caEncodedDesign(design.ort) #水準をコード化
# レンズ ミラー 本体の色 センサーサイズ HDR機能 電子水準器 動画撮影 WiFi
# 1 1 1 1 1 1 1 1 1
# 16 2 2 2 2 1 1 1 1
# 61 1 1 2 2 2 2 1 1
# 92 2 2 1 2 2 1 2 1
# 99 1 2 1 1 1 2 2 1
# 118 2 1 2 1 2 2 2 1
# 146 2 1 1 1 2 1 1 2
# 168 2 2 2 1 1 2 1 2
# 187 1 2 1 2 2 2 1 2
# 205 1 1 2 2 1 1 2 2
# 215 1 2 2 1 2 1 2 2
# 234 2 1 1 2 1 2 2 2
cor(caEncodedDesign(design.ort)) #相関係数で見ると見事に直交している
# レンズ ミラー 本体の色 センサーサイズ HDR機能 電子水準器 動画撮影 WiFi
# レンズ 1 0 0 0 0 0 0 0
# ミラー 0 1 0 0 0 0 0 0
# 本体の色 0 0 1 0 0 0 0 0
# センサーサイズ 0 0 0 1 0 0 0 0
# HDR機能 0 0 0 0 1 0 0 0
# 電子水準器 0 0 0 0 0 1 0 0
# 動画撮影 0 0 0 0 0 0 1 0
# WiFi 0 0 0 0 0 0 0 1

15. 分析の実行
• 実データが無いのでconjointパッケージに
入っているサンプルデータで。
• お茶の調査データ
– 属性と水準と組み合わせ
• price:３水準(low, medium, high)
• variety:3水準(black, green, red)
• kind:3水準(bags, granulated, leafy)
• aroma:２水準(yes, no)
– 100名に13通りの組み合わせを10点満点で評価
させたデータ。

16. サンプルデータの呼び出し
# データセットの呼び出し
data(tea)
# 組み合わせの表示。13通り（4属性（3水準、3水準、3水準、2水準））
print(tprof) # コード化された状態。
# price variety kind aroma
# 1 3 1 1 1
# 2 1 2 1 1
# 3 2 2 2 1
# 4 2 1 3 1
# 5 3 3 3 1
# 6 2 1 1 2
# 7 3 2 1 2
# 8 2 3 1 2
# 9 3 1 2 2
# 10 1 3 2 2
# 11 1 1 3 2
# 12 2 2 3 2
# 13 3 2 3 2

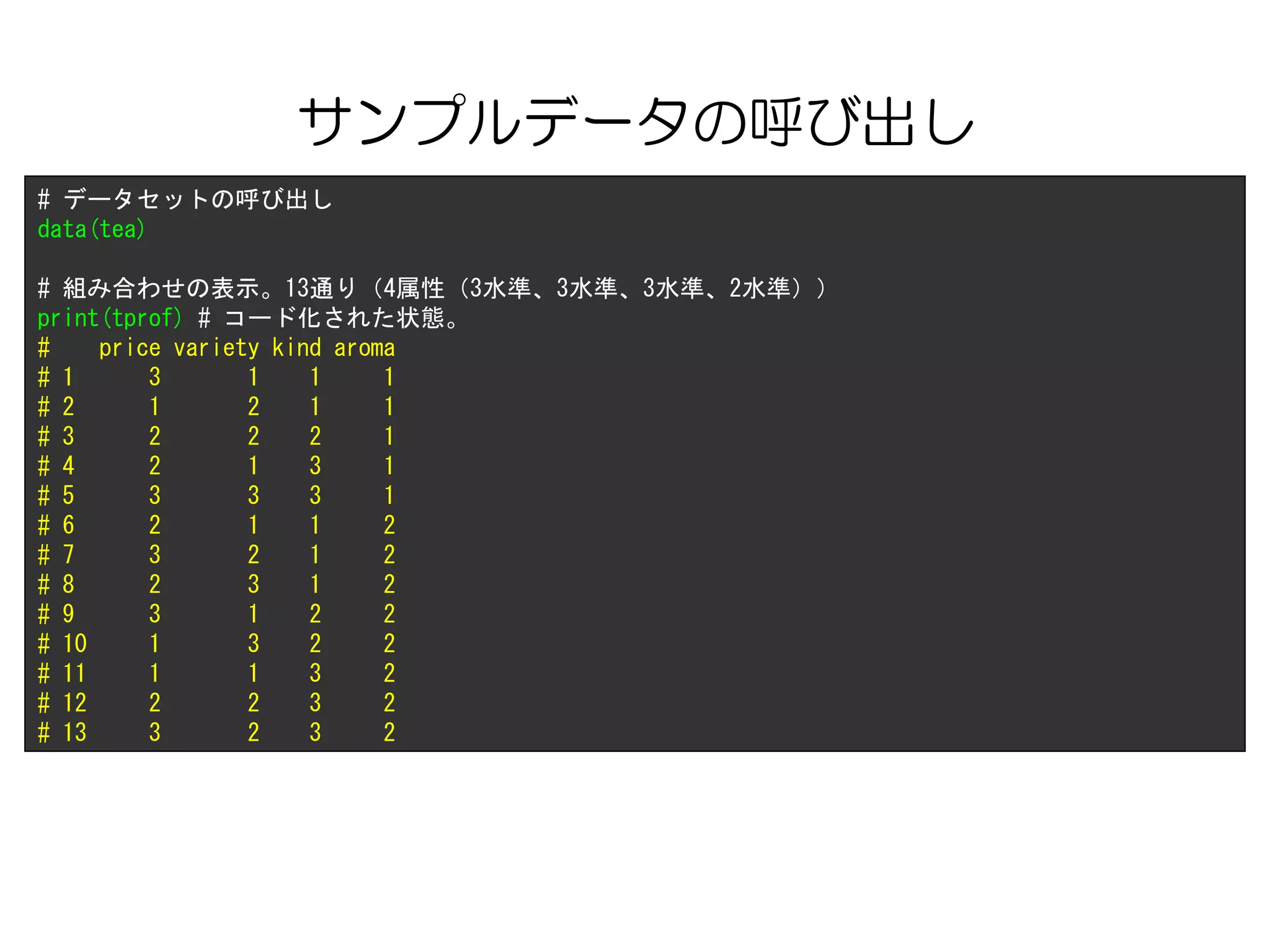
17. サンプルデータの呼び出し
# 各水準のラベル
print(tlevn)
# levels
# 1 low
# 2 medium
# 3 high
# 4 black
# 5 green
# 6 red
# 7 bags
# 8 granulated
# 9 leafy
# 10 yes
# 11 no
# 選好マトリクス。数値が大きい方が高評価。
head(tprefm) #100名×13組み合わせ。全部表示させると煩雑なのでhead()で一部のみ表示。
# profil1 profil2 profil3 profil4 profil5 profil6 profil7 profil8 profil9 profil10 profil11 profil12 profil13
# 1 8 1 1 3 9 2 7 2 2 2 2 3 4
# 2 0 10 3 5 1 4 8 6 2 9 7 5 2
# 3 4 10 3 5 4 1 2 0 0 1 8 9 7
# 4 6 7 4 9 6 3 7 4 8 5 2 10 9
# 5 5 1 7 8 6 10 7 10 6 6 6 10 7
# 6 10 1 1 5 1 0 0 0 0 0 0 1 1

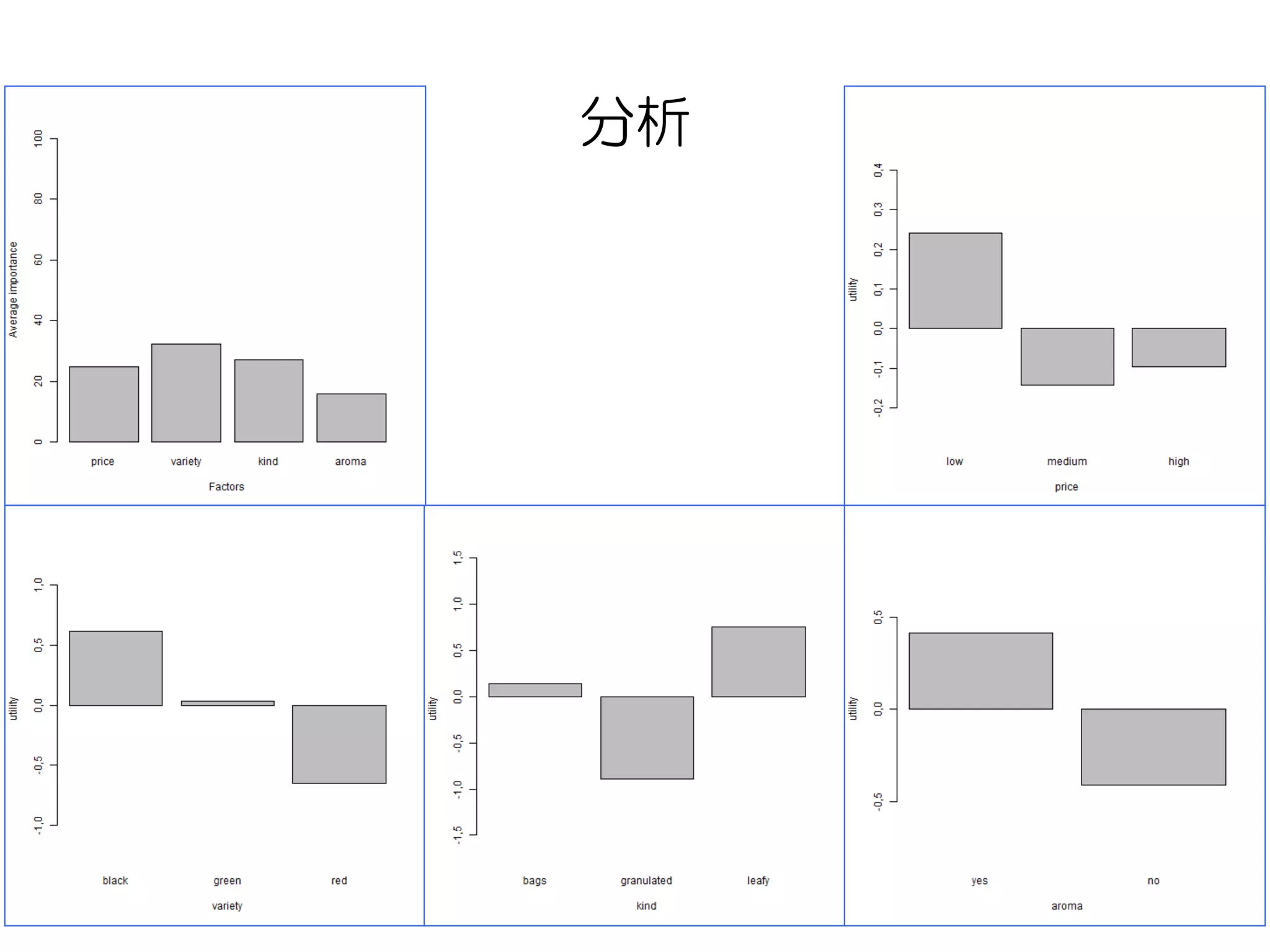
18. 分析
# 引数は順に選好マトリクス、組み合わせ、水準のラベル
# 分析結果の値と同時に効用値と重要度のグラフが出力される。
Conjoint(tprefm, tprof, tlevn)
# [1] "Part worths (utilities) of levels (model parameters for whole sample):"
# levnms utls
# 1 intercept 3,5534
# 2 low 0,2402
# 3 medium -0,1431
# 4 high -0,0971
# 5 black 0,6149
# 6 green 0,0349
# 7 red -0,6498
# 8 bags 0,1369
# 9 granulated -0,8898
# 10 leafy 0,7529
# 11 yes 0,4108
# 12 no -0,4108
# [1] "Average importance of factors (attributes):"
# [1] 24,76 32,22 27,15 15,88
# [1] Sum of average importance: 100,01
# [1] "Chart of average factors importance"
効用値
重要度

19. 分析
効用値

20. ベネフィット・セグメンテーション
• 人には好みというものがある。好みの傾向が
似た人たちをグループ化したい。
• そこで、コンジョイント分析で得られた個人別
の効用値に基づいてクラスター分析を行う。

21. ベネフィット・セグメンテーション
# 引数は順に選好マトリクス、コード化した組み合わせ、分けたいクラスタの数
segments <- caSegmentation(tprefm, tprof, 4)
segments
# K-means clustering with 4 clusters of sizes 44, 13, 26, 17
#
# Cluster means:
# (省略)
# Clustering vector:
# [1] 1 2 3 4 4 1 3 2 4 3 3 3 1 1 1 1 2 1 4 1 1 3 1 4 3 1 2 3 4 4 1 3 2 4 3 3 3
# [38] 1 1 1 1 2 1 4 1 3 3 1 1 1 3 1 1 1 4 3 1 4 1 2 1 1 3 3 2 3 1 1 1 4 3 1 1 2
# [75] 3 4 4 1 3 1 2 3 4 3 1 1 1 1 2 1 2 1 4 1 1 3 1 2 4 3
# （以下略）
# segments$cluster とすればどのクラスタ番号が得られるので、他のデータと組み合わせて使う。

22. Enjoy!