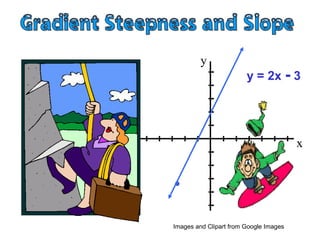
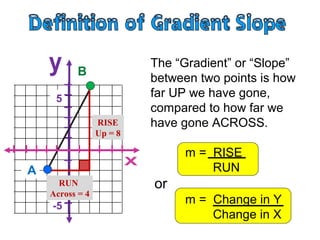
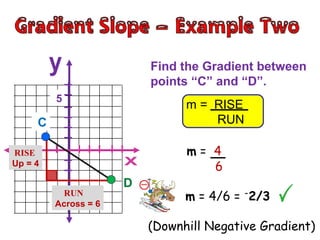
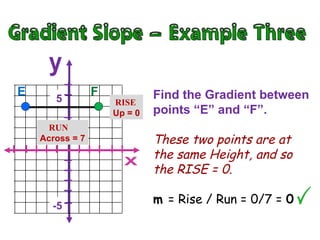
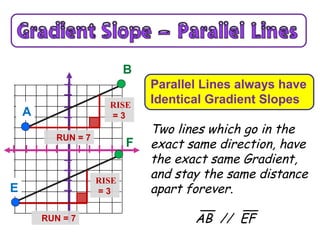
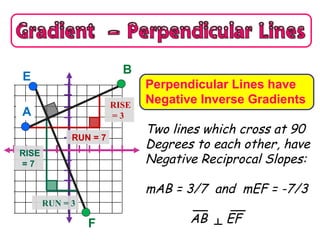
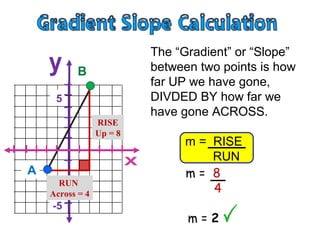
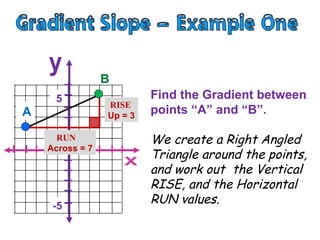
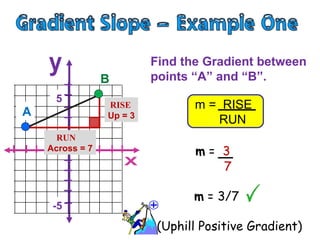
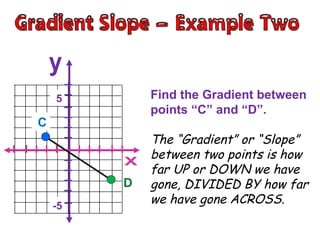
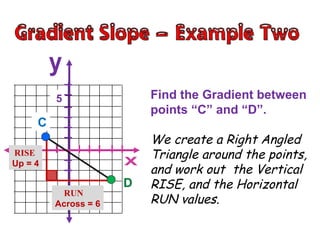
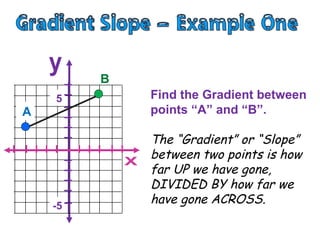
- The gradient or slope represents how steep a slope is, with uphill slopes being positive and downhill slopes being negative. - The gradient is measured by the rise over the run, where rise is the vertical change in distance and run is the horizontal change in distance between two points. - To find the gradient between two points, you create a right triangle between the points and calculate the rise as the vertical leg and the run as the horizontal leg, then plug those values into the formula: Gradient = Rise/Run.

1. x
y
y = 2x - 3
Images and Clipart from Google Images

2. Gradient represents how steep a slope is :
Uphill is Positive, and Downhill slopes are Negative.
The Gradient symbol is “m” for how “mountainous” a slope is.
Rene Descartes invented Gradient, and assigned the letter
“m” as “montagne”, which is French for Mountain.

3. As we go up the mountain, it becomes
steeper. (Positive Increase)
As we go up the mountain it gets cooler,
with progressively less soil and plants.
(Negative Decrease, downhill graphs).
Distance up
Mountain
Steepness
Distance up
Mountain
Temperature
Distance up
Mountain
Soil&Vegetation

4. There are four types of “Gradient” or “Slope”
Images Purchased from Photozone.com

5. m = UP = 2
ACROSS 2
RUN
Across = 2
RISE
Up = 2
The “Gradient” or “Slope” is
measured as how far UP we
have gone, compared to how
far we have gone ACROSS.
= 1
Cycling Image Purchased from Photozone.com

6. 5
-5
The “Gradient” or “Slope”
between two points is how
far UP we have gone,
compared to how far we
have gone ACROSS.
m = RISE
RUN
or
m = Change in Y
Change in X
A
B
RUN
Across = 4
RISE
Up = 8

7. 5
-5
The “Gradient” or “Slope”
between two points is how
far UP we have gone,
DIVDED BY how far we
have gone ACROSS.
m = RISE
RUN
m = 8
4
m = 2
A
B
RUN
Across = 4
RISE
Up = 8

8. Step 1 - Have two points that are on a straight line
Step 2 - Work out the Vertical and Horizontal Distances
Step 3 - Substitute the Step 2 values into the Gradient Slope
formula:
Step 4 - Reduce Down Fraction Answers to simplest form
Step 5 Write Gradient Slope value as Positive
for Uphill and Negative for Downhill.
m = RISE (Vertical Change)
RUN (Horizontal Change)

9. B
5
-5
Find the Gradient between
points “A” and “B”.
The “Gradient” or “Slope”
between two points is how
far UP we have gone,
DIVIDED BY how far we
have gone ACROSS.
A

10. B
5
-5
Find the Gradient between
points “A” and “B”.
We create a Right Angled
Triangle around the points,
and work out the Vertical
RISE, and the Horizontal
RUN values.
A
RUN
Across = 7
RISE
Up = 3

11. B
5
-5
Find the Gradient between
points “A” and “B”.
A
RUN
Across = 7
RISE
Up = 3
m = RISE
RUN
m = 3
7
m = 3/7
(Uphill Positive Gradient)

12. D
5
-5
Find the Gradient between
points “C” and “D”.
The “Gradient” or “Slope”
between two points is how
far UP or DOWN we have
gone, DIVIDED BY how far
we have gone ACROSS.
C

13. D
5
-5
Find the Gradient between
points “C” and “D”.
We create a Right Angled
Triangle around the points,
and work out the Vertical
RISE, and the Horizontal
RUN values.
C
RUN
Across = 6
RISE
Up = 4

14. D
5
-5
Find the Gradient between
points “C” and “D”.
C
RUN
Across = 6
RISE
Up = 4
m = RISE
RUN
m = 4
6
m = 4/6 = -
2/3
(Downhill Negative Gradient)

15. E F
5
-5
Find the Gradient between
points “E” and “F”.
These two points are at
the same Height, and so
the RISE = 0.
m = Rise / Run = 0/7 = 0
RUN
Across = 7
RISE
Up = 0

16. F
B
Parallel Lines always have
Identical Gradient Slopes
Two lines which go in the
exact same direction, have
the exact same Gradient,
and stay the same distance
apart forever.
AB // EF
A
RUN = 7
RISE
= 3
E
RUN = 7
RISE
= 3

17. F
B
Perpendicular Lines have
Negative Inverse Gradients
Two lines which cross at 90
Degrees to each other, have
Negative Reciprocal Slopes:
mAB = 3/7 and mEF = -7/3
AB _ EF
A
RUN = 7
RISE
= 3
E
RUN = 3
RISE
= 7

18. Blank X-Y Grid
-3 3
5
-5

19. http://passyworldofmathematics.com/