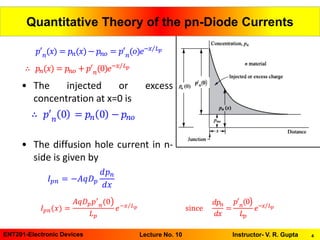
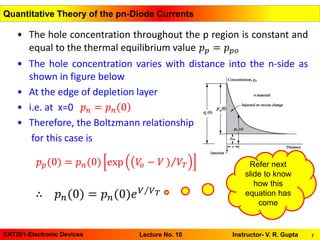
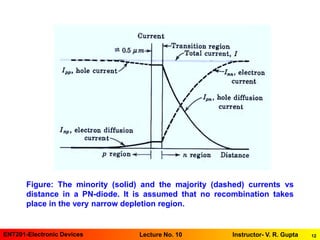
The document is a presentation on the quantitative theory of pn-diode currents, focusing on the diode current equation and its dependence on applied voltage. It discusses the behavior of hole and electron currents across the junction and provides mathematical representations for these currents. Additionally, the presentation includes reading assignments from Milliman's textbooks to further explore the topic.