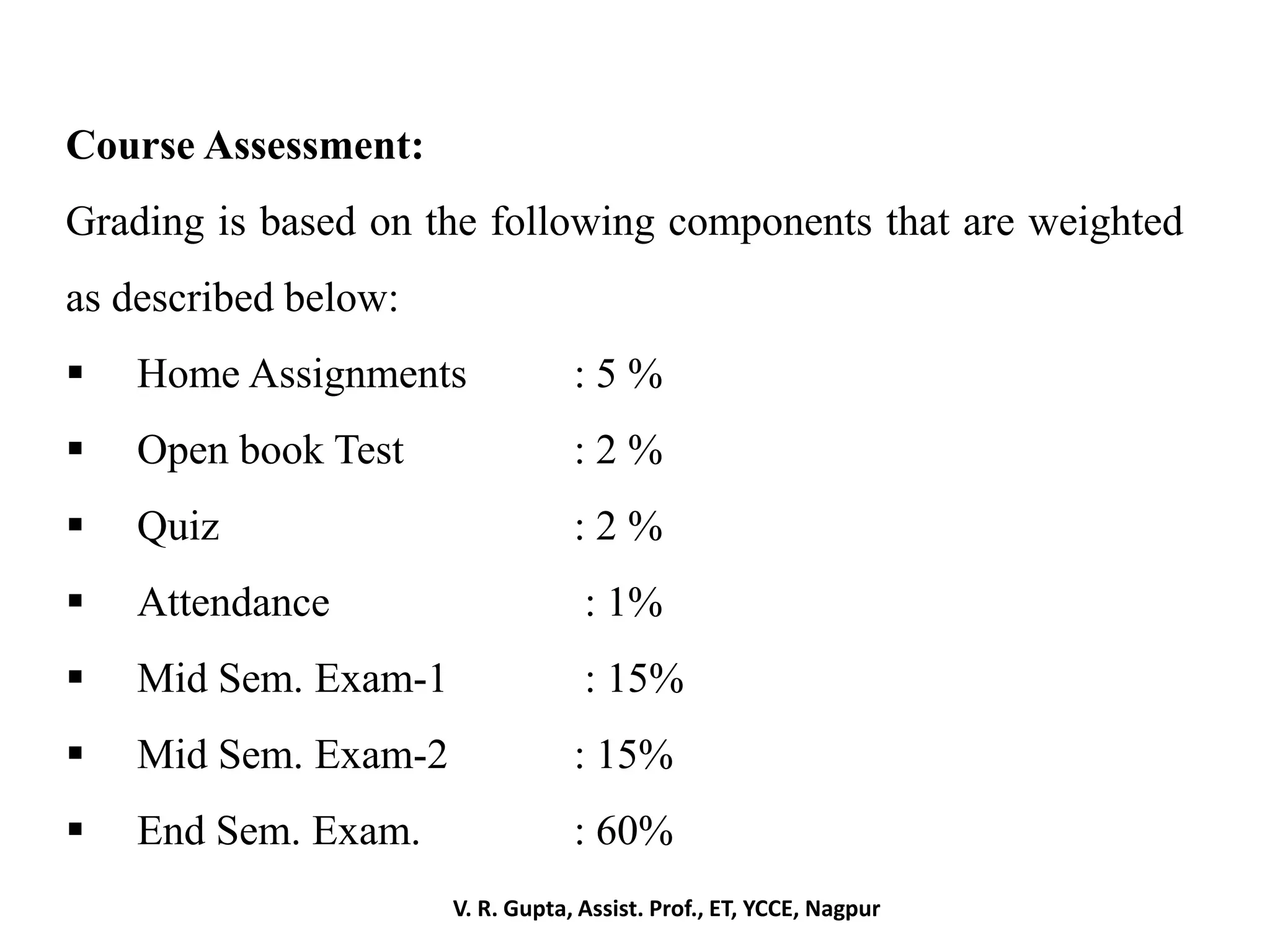
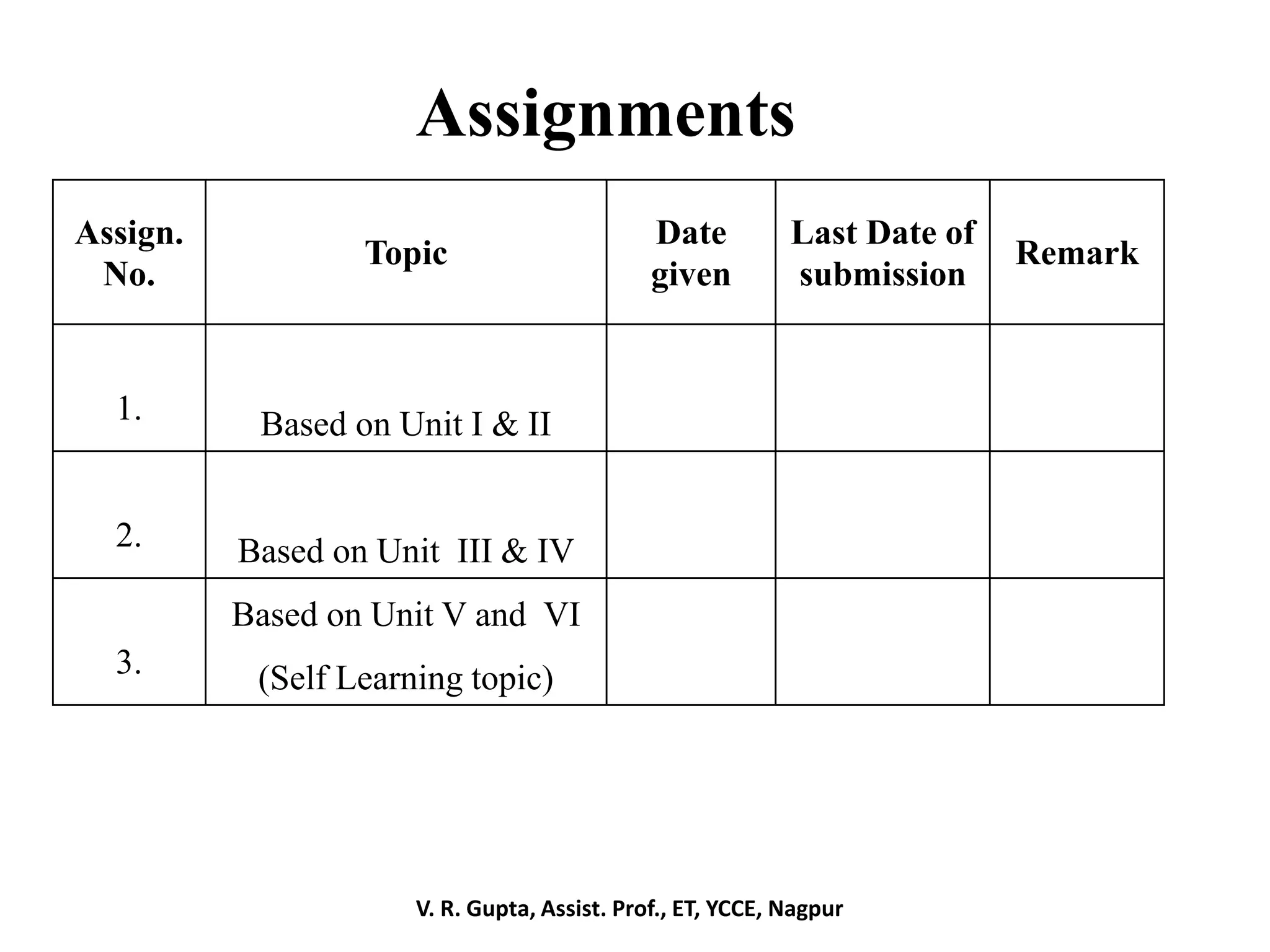
This document describes a course on mathematical foundations for communication engineering. The course objectives are to develop understanding of probability theory, random variables, and sequences of random variables. Key topics covered include probability, random variables, functions of random variables, special distributions, sequences of random variables, and random processes. Assessment is based on assignments, tests, exams, attendance, and a final exam weighting 60%. The course aims to enable students to apply probability concepts in practical problems and communication systems analysis.












![V. R. Gupta, Assist. Prof., ET, YCCE, Nagpur
2nd Die
1st Die
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12
The total no of outcomes is 36 if we keep the Dice distinct.
The number of ways of getting a seven is N7 = 6.
6 1
[ 7]
36 6
P getting a ](https://image.slidesharecdn.com/fmce-170425144252/75/Introduction-to-Probability-15-2048.jpg)
![Probability as a Measure of Frequency of
occurrence
• The Probability of an event E is computed as.
•
• here and therefore
• We can never perform the experiment an infinite number of
times so we can only estimate P[E] from a finite number of
trials.
• We postulate that approaches a limit as n goes to
infinity.
V. R. Gupta, Assist. Prof., ET, YCCE, Nagpur
[ ] lim E
n
n
P E
n
En n 0 [ ] 1P E
En n](https://image.slidesharecdn.com/fmce-170425144252/75/Introduction-to-Probability-16-2048.jpg)










![Partitions
1
1
........ { }
,
,........,[ ]
n i j
n
A A S where A A j i
Thus
A AU
U U
A partitions U of a set S is a collection
of mutually exclusive subsets Ai of S
whose union equals S.
A1
A2
An
B
V. R. Gupta, Assist. Prof., ET, YCCE, Nagpur](https://image.slidesharecdn.com/fmce-170425144252/75/Introduction-to-Probability-27-2048.jpg)








![Axiomatic definition of Probability
Probability is a set function P[.] that assigns to every event E a
number P[E] called the probability of E such that
1. P[E] ≥ 0
2. P[Ω] =1
3. P[E U F]=P[E]+P[F] If EF= ϕ
These conditions are the axioms of the theory of probability
V. R. Gupta, Assist. Prof., ET, YCCE, Nagpur](https://image.slidesharecdn.com/fmce-170425144252/75/Introduction-to-Probability-36-2048.jpg)
![Properties
The probability of the impossible event is zero.
These conditions are the axioms of the theory of probability
4. [ ] 0
5. [ ] [ ] [ ]
6. [ ] 1 [ ]
7. [ ] [ ] [ ] [ ]
8. [ ] [ ] [ ]
c
c
c
P
P EF P E P EF
P E P E
P E F P E P F P EF
P E P B P AB iff B A
U
V. R. Gupta, Assist. Prof., ET, YCCE, Nagpur](https://image.slidesharecdn.com/fmce-170425144252/75/Introduction-to-Probability-37-2048.jpg)
