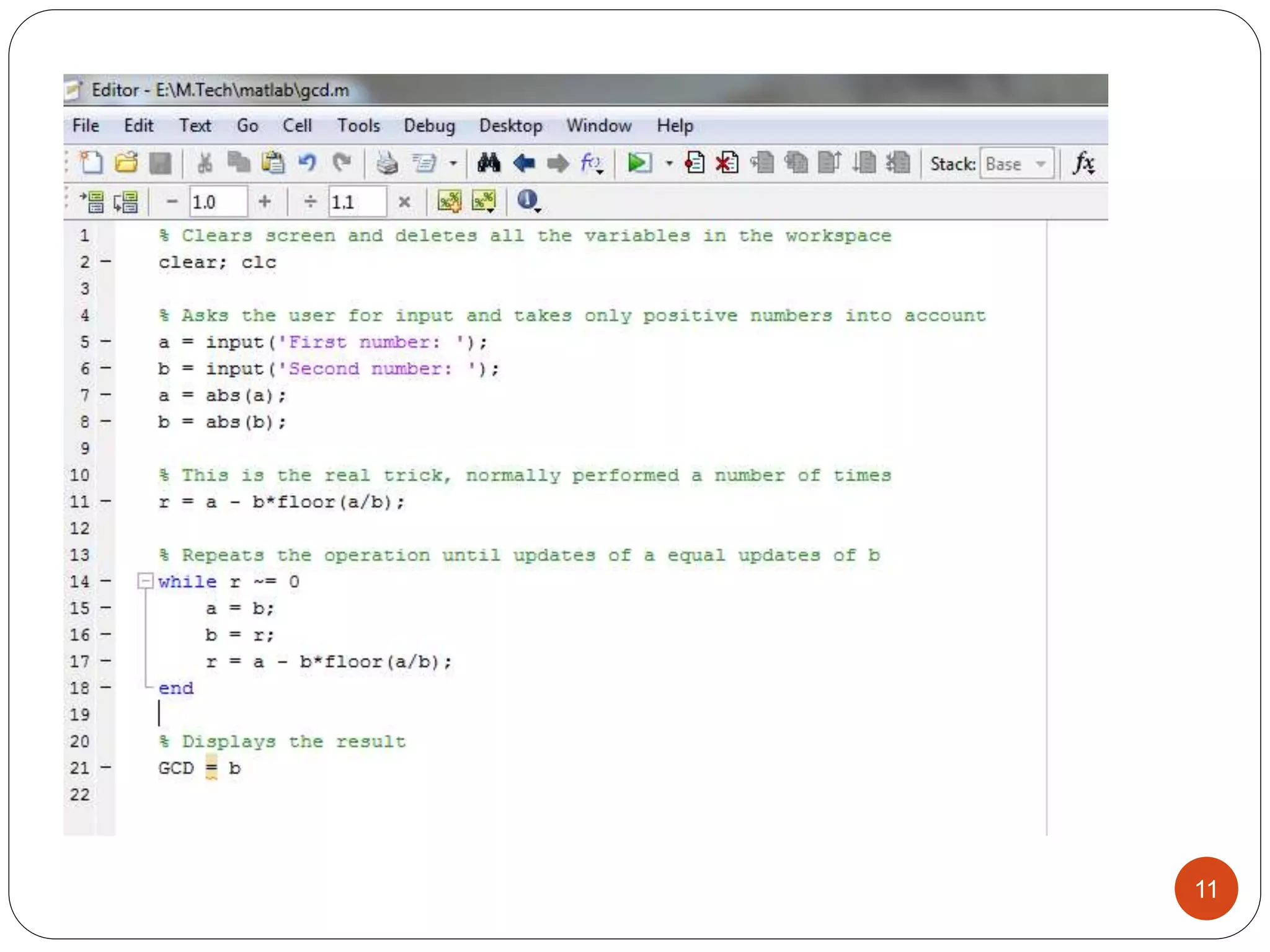
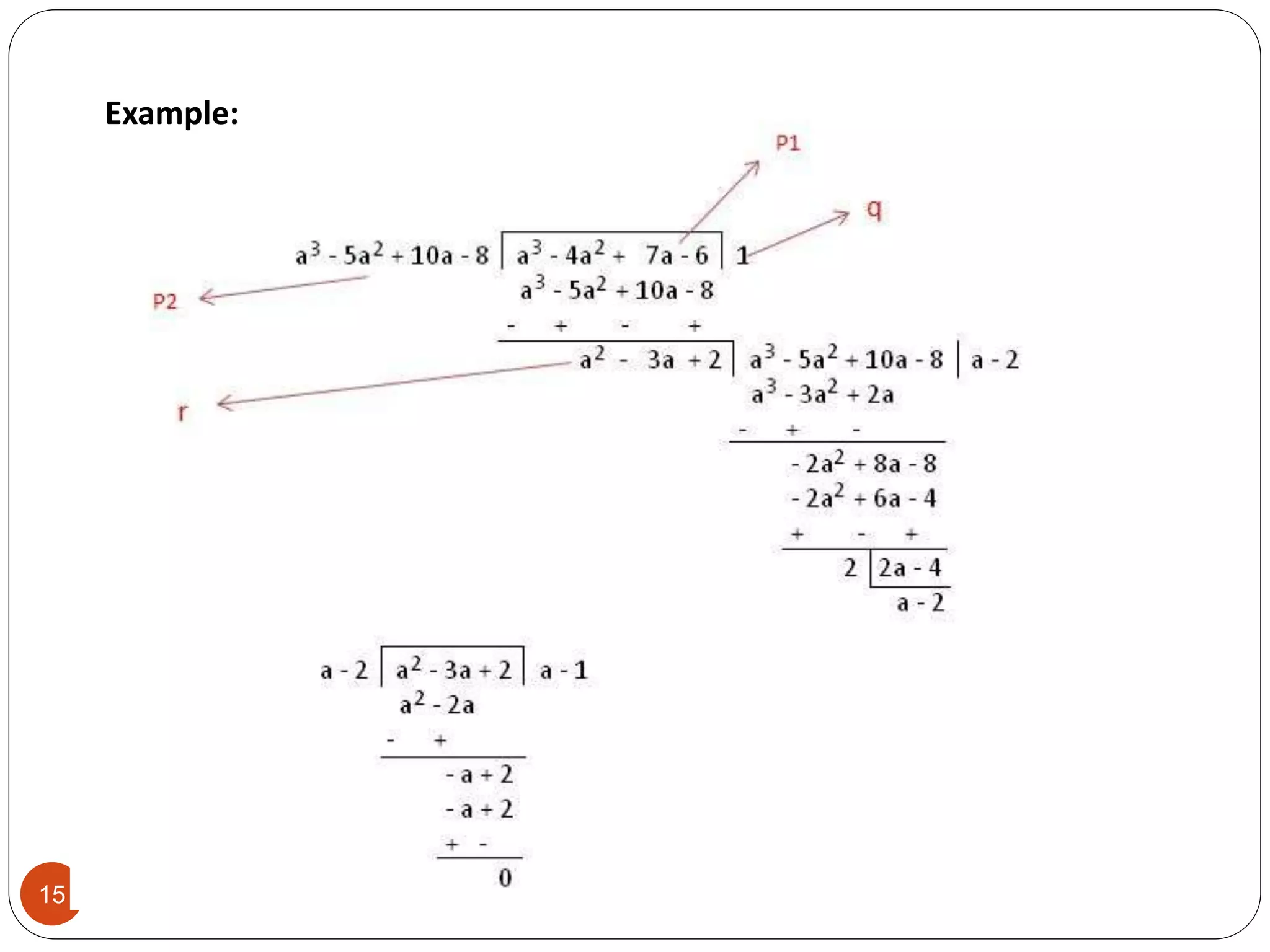
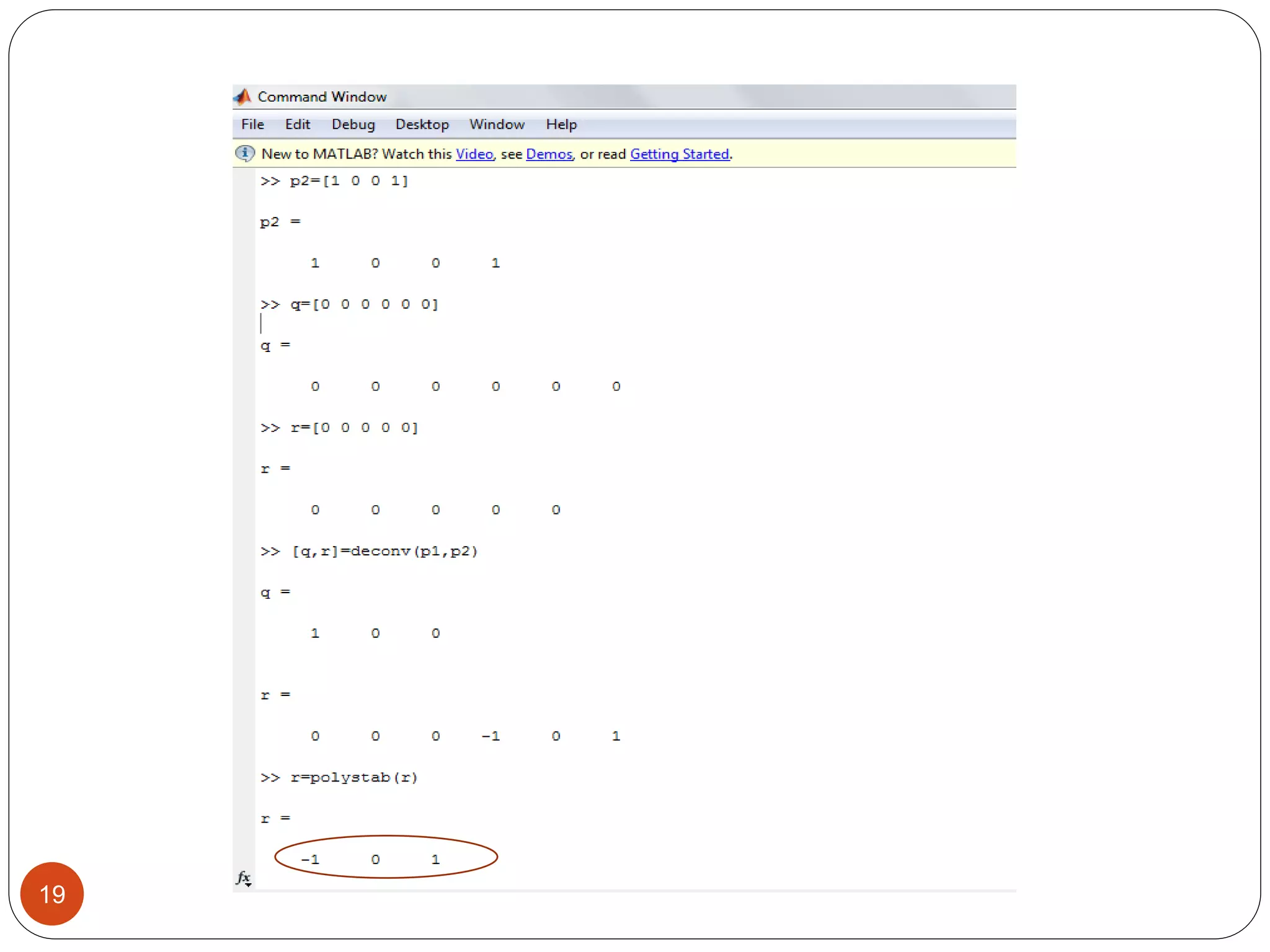
This document discusses the Euclidean algorithm for finding the greatest common divisor (GCD) of integers and polynomials. It begins with an introduction and definitions of GCD and the Euclidean algorithm. It then provides the steps of the Euclidean algorithm, applications, and MATLAB code examples to calculate the GCD of integers and polynomials. The document concludes with future work plans to improve the polynomial GCD MATLAB code and implement GCD algorithms in Verilog code targeting FPGAs.







![Properties of GCD:
8
Gcd(a,0)=a
Gcd(a,a)=a
Gcd(a,b)=gcd(b,a mod b)
a mod b=a-b [floor(a/b)]](https://image.slidesharecdn.com/eucledianalgorithmforgcdofintegersandpolynomials-151221094949/75/Eucledian-algorithm-for-gcd-of-integers-and-polynomials-8-2048.jpg)