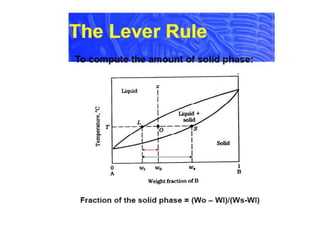
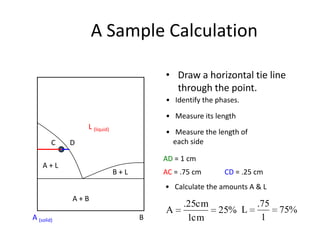
The document describes the lever rule, which is used to determine both the compositions of phases present at a given temperature in a multi-phase alloy system, as well as the relative amounts of each phase. It explains that a tie line is drawn through the given composition point on a phase diagram. The intercepts of the tie line with phase boundaries indicate the compositions of the phases. The relative amounts of each phase are inversely proportional to the distances from the composition point to the intercepts with each phase boundary.

1. LEVER RULE
Prof. H. K. Khaira
Professor in MSME Deptt.
MANIT, Bhopal

2. Lever Rule
• The compositions of the two coexisting phases at a
point in a two phase region is given by the points of
intersection of the tie line from that point with the
boundaries of the respective phases.
• The relative amounts of two coexisting phases at a
point are INVERSELY proportional to the distances of
the point from intersection points of the tie line from
the point with the phase boundaries.”
2

3. Lever Rule
• It is also possible to determine how much of each phase exists at
the given temperature using the lever rule.
• It is important to know the amounts of each phase present because
the properties of the alloy depend on the amount of each phase
present.
• The lever rule uses the tie line and the basic scientific principle of
the conservation of mass to determine the ratio of the two phases
present.
• The tie-line gives the chemical compositions of each of the two
phases, and the combined amounts of these two compositions
must add up to the alloy's overall composition (Co), which is known.
• In other words, Co must be composed of the appropriate amount of
α of composition Cα and of liquid of Cliq.

4. Lever Rule
1. Simply by looking at a phase diagram it is possible to tell what phase or
phases an alloy will have at a given temperature.
2. But, it is also possible to get quantitative information from the diagram.
3. Consider the alloy at the temperature shown on the phase diagram.
It is easy to see that at this temperature, it is a mixture of alpha and liquid
phases.

5. Lever Rule
4. It is easy to see that at this temperature, it is a mixture of alpha and liquid
phases.
5. Using a tie lin,e it is also possible to determine the composition of the
phases at this temperature.
6. A tie line is an isothermal (constant temperature) line drawn through the
alloy's position on the phase diagram when it is in a two phase field.

6. Lever Rule
7. The points where the ends of the tie line intersect the two adjacent solubility
curves indicate the compositions of the two phases that exist in equilibrium at this
temperature.
8. In this example, the tie line shows that the alpha phase is 5.2%B and the liquid
phase is 34.5%B at this temperature.
9. It is important to keep in mind that the tie rule addresses the determination of the
compositions of the constituent phases within the sample and it does not address the
overall chemical composition of the sample, which remains unchanged.

7. Lever Rule
• So basically, the proportions of the phases present are given by the
relative lengths of the two sections of the tie line.
• The fraction of alpha phase present is the given by the ratio of the
Co to Cliq portion of the tie line and the total length of the tie line
(Cliq to Cα). Mathematically the relationships can be written as
fα = (Cliq – Co)/(Cliq - Cα).
• The fraction of liquid phase present is given by the ratio of the Co to
Cα portion of the tie line and the total length of the tie line (Cliq to
Cα). Mathematically this relationships can be written as
fliq = (Co - Cα)/(Cliq - Cα).
• Of course, the two values must total to equal one.

8. Lever Rule
• Note that the right side of the tie line gives the
proportion of the phase on the left (α phase in
this example) and left side of the tie line gives the
proportion of the phase to the right (liquid phase
in this example).
• It is easy to keep this relationship straight by
simply considering what the ratio would be near
one of the tie line intersect points.
• For example, if Co were near the liquidus line the
ratio of the liquid section of the line to the total
length of the line will be nearly one.

9. Lever Rule

10. Translating This Statement
• “two coexisting phases”
Means you are in a 2 phase
region.
Pick an arbitrary point C.
• There are two phases at point C.
• These phases are A an B
• Hence Phases A and B will be
in equilibrium at point C
•
L
A+L
B+L
C
P
Q
A+B
A
B

11. Tie Lines
The line from A to B through C is a tie line.
A tie line is,
• An isothermal line
• That connects two equilibrium phases

12. Compositions of Phases Present
The tie line from point C
intersect boundaries of
phase A and B at 0% A and
0% B respectively.
Hence the composition of
phase A will be 0% B or
pure A.
Similarly, the composition of B
will be pure B or 0% A.
L
A+L
B+L
C
A+B
A
B

13. Amounts of Phases Present
“The intercepts of the tie line
with the phase boundaries A
and B are PC and CQ
respectively.
“The amounts of phase A and B
are inversely proportional to
the intercept of tie line with
the phase boundaries.
• “The amounts are inversely
proportional” Means
• PC / PQ is the fraction of B
And,
L
A+L
B+L
C
P
Q •
A+B
A
B
CQ / PQ is the fraction of A

15. A Sample Calculation
• Draw a horizontal tie line
through the point.
• Identify the phases.
• Measure its length
L (liquid)
C
• Measure the length of
each side
D
AD = 1 cm
A+L
B+L
AC = .75 cm
CD = .25 cm
• Calculate the amounts A & L
A+B
A (solid)
B
A
.25cm
1cm
25% L
.75
1
75%

16. Summary
• The lever rule is used to determine the compositions of the
phases present.
• The lever rule is also used to calculate the relative percents of
each phase when 2 or more phases are present.
• The first step in lever rule calculation is to draw a tie line
through the composition.
• The points of intercepts gives the compositions of the phases
• Next one measures the lengths of the tie line, and the distance
from the composition to each phase.
• The relative amounts of a phase is proportional to the distance
from the other phase to the composition, divided by the length
of the tie line. (Opposite length / total length)