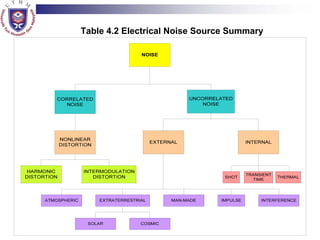
This document discusses different types of noise in communication systems. It defines random variables and random processes that are used to model noise. There are two main types of random variables: discrete and continuous. Noise can be modeled as random processes. Thermal noise arises from the random motion of electrons and is well modeled by a Gaussian process. Other types of noise discussed include shot noise and transit time noise. External noise sources include atmospheric noise, extraterrestrial noise from space, and man-made noise. Internal noise is generated within devices and circuits. White noise is defined as having a constant power spectral density across all frequencies.


















![The Q function represent the area under the tail of a standard random
variable.
It is well tabulated and used in analyzing the performance of
communication system.
Q(x) satisfy the following relations:
(4.3a)
Q(-x) = 1 – Q(x)
(4.3b)
Q(0) = ½
Q(∞) = 0
(4.3c)
Table 3.1 gives the value of this function for various value of x.
For Ν(m, σ2) random variable, a simple change of variable in the integral
that computes P(X > x) results in P(X > x) = Q[(x – m)/σ].
tail probability in Gaussian random variable.
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-19-320.jpg)
















![NOISE POWER
Noise power is given as
N0
df
−B 2
= N0 B
PN = ∫
B
and can be written as
PN = kTB [W]
(3.6)
(3.7)
where
PN = noise power,
k = Boltzmann’s constant (1.38x10-23 J/K)
B = bandwidth,
T = absolute temperature (Kelvin)(17oC or 290K)
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-36-320.jpg)















![Example 4.8
For an amplifier with an output signal power of 10 W and an output noise
power of 0.01W, determine the S/N.
Ans
S/N =
10
= 1000
[unitless ]
0.01
S / N ( dB ) = 10 log 1000 = 30 [ dB ]
Example 4.9
For an amplifier with an output signal voltage of 4 V, an output noise voltage
of 0.005 V and an input and output resistance of 50 Ω, determine the S/N.
Ans
Vs
S/N =
VN
2
R =
2
42
= 640000
[unitless]
0.0052
S / N ( dB ) = 10 log 640000 = 58 [ dB ]
R
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-53-320.jpg)
![NOISE FACTOR (F) & NOISE FIGURE (NF)
Noise factor and noise figure are figures of merit to indicate how much a
signal deteriorate when it pass through a circuit or a series of circuits
Noise factor
F=
Noise figure
input signal-to-noise ratio
[unitless]
output signal-to-noise ratio
input signal-to-noise ratio [dB]
NF = 10log
output signal-to-noise ratio
= 10log F
(4.15)
(4.16)
For perfect noiseless circuit, F = 1, NF = 0 dB
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-54-320.jpg)
![For ideal noiseless amplifier with a power gain (AP), an input signal power
level (Si) and an input noise power level (Ni) as shows in Figure 4.12 (a).
The output signal level is simply APSi, and the output noise level is APNi.
Ap Si
Sout
Si
=
=
N out Ap N i N i
[unitless]
(4.17)
Figure 4.12 (b) shows a nonideal amplifier that generates an internal noise
Nd
Ap Si
Sout
Si
=
=
N out Ap N i + N d N i + N d Ap
[unitless]
(4.18)
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-55-320.jpg)

![When two or more amplifiers are cascaded as shown in Figure
4.13, the total noise factor is the accumulation of the
individual noise factors. Friiss’ formula is used to calculate the
total noise factor of several cascaded amplifiers.
Mathematically, Friiss formula is
Fn − 1
F2 − 1 F3 − 1
[unitless] (4.19)
FT = F1 +
A1
+
A1 A2
+
A1 A2 ..... An −1
Figure 4.13 Noise figure of cascaded amplifiers
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-57-320.jpg)
![Where
FT = total noise factor for n cascaded amplifiers
F1, F2, F3…n = noise factor, amplifier 1,2,3…n
A1, A2…. An = power gain, amplifier 1,2,…..n
Notification remarks
Change unit of all noise factors F and power gains A from [dB]
to [unitless] before insert its into Friss formula equation
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-58-320.jpg)
![Example 4.10
The input signal to a telecommunications receiver consists of 100 μW of
signal power and 1 μW of noise power. The receiver contributes an
additional 80 μW of noise, ND, and has a power gain of 20 dB. Compute
the input SNR, the output SNR and the receiver’s noise figure.
Ans.
a) Input SNR =
Si
100 × 10 -6
=
= 100 [ unitless ]
-6
Ni
1 × 10
Input SNR(dB) = 10 log 100 = 20 [ dB ]
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-59-320.jpg)
![b) The output noise power = internal noise + amplified input noise
N out = N D + Ap N i = 80 μW + (100 × 1× 10 −6 W )
1.8 × 10 − 4 [W ]
=
The output signal power = amplified input signal
S out = Ap Si = 100 × 100 × 10 −6
× 10 − 2 [W ]
=1
S out
1× 10 -2
Output SNR=
=
= 55.56[unitless ]
-4
N out 1.8 × 10
Output SNR(dB) =
10 log 55 .56 = 17 .45[ dB ]
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-60-320.jpg)
![c) Noise Figure NF = 10 log
input SNR[unitless ]
100
= 10 log
output
SNR[unitless ]
55.56
= 2 . 55 [ dB ]
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-61-320.jpg)

![Ans
a) Input SNR
S i 2 × 10 -10
=
= 1 × 10 8 [unitless ]
N i 2 × 10 -18
10
Input SNR(dB) = log 100000000 = 80 [ dB ]
b) The output noise power Nout = ND + Ap Ni = 6×10−12 + (1×106 × 2×10−18)
×10−12[W ]
=8
The output signal power S out = Ap Si = 1×106 × 2 ×10 −10
2 ×10 − 4 [W ]
=
2 × 10 -4
= 74 [ dB ]
Output SNR(dB) = 10 log
- 12
8 × 10
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-63-320.jpg)
![c)
Noise factor F =
input SNR [ unitless ] 100000000
=
= 4[ unitless ]
output SNR [unitless ]
25000000
Noise figure NF = 10 log 4 = 6.02[ dB ]
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-64-320.jpg)
![Example 4.12
For three cascaded amplifier stages, each with noise figures of 3 dB and power
gains of 10 dB, determine the total noise figure.
Ans.
Change all noise figure and power gain from [dB] unit to [unitless]
10
Power gain A = A = A = 10 10 = 10[unitless ]
1
2
3
3
10
Noise Factor F1 = F2 = F3 = 10 = 2[unitless ]
Using Friss formula ,
F − 1 F3 − 1
+
[unitless ]
Total noise factor FT = F1 + 2
A1
A1 A2
2 −1 2 −1
= 2+
+
10 10 × 10
[unitless ]
= 2.11
Total noise figure NFT = 10 log 2 . 11 = 3 . 24 [ dB ]
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-65-320.jpg)


![Example 4.13
Determine,
a) Noise figure for an equivalent noise temperature of 75 K.
b) Equivalent noise temperature for noise figure of 6 dB.
Ans.
a) Noise factor F = 1 + Te = 1 + 75 = 1 .258 [unitless ]
290
T
Noise figure NF = 10 log 1 . 258 = 1[ dB ]
b) Noise factor F = anti log(
NF
6
) = anti log( ) = 4[unitless]
10
10
Equivalent noise temperature Te = T ( F − 1) = 290 ( 4 − 1)
870[ K ]
=
Dept. Of Communication Engineering,
Faculty Of Electrical And Electronics,
Universiti Tun Hussein Onn Malaysia](https://image.slidesharecdn.com/chapter4noise-131124005538-phpapp01/85/Theory-Communication-68-320.jpg)