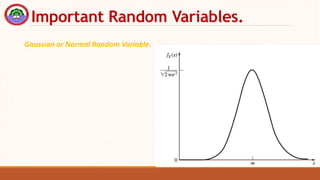
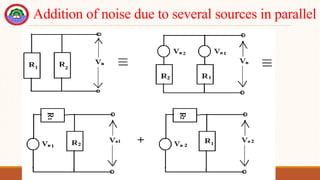
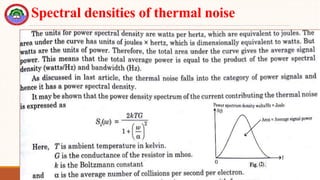
The document provides an overview of probability theory and random processes relevant to communication systems. It explains fundamental concepts including deterministic and stochastic signals, probability definitions, joint and marginal probabilities, and introduces various random variables such as Bernoulli, binomial, and Gaussian. Additionally, it describes statistical measures like expected value, autocorrelation, and the properties of power spectral density in relation to random processes.









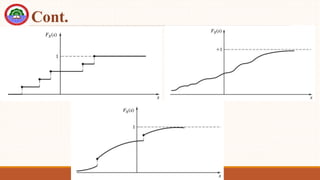
![Cont.
Definition: The cumulative distribution function (cdf) assigns a probability
value for the occurrence of x within a specified range such that FX(x) = P[X
≤ x].
Properties:
◦ 0 ≤ FX(x) ≤ 1
◦ FX(x1) ≤ FX(x2), if x1 ≤ x2
For discrete random variables FX(x) is a stair-case function.
Examples of CDFs for discrete, continuous, and mixed random variables
are shown](https://image.slidesharecdn.com/chapter-4combined-230707191204-768bd611/85/Chapter-4-combined-pptx-10-320.jpg)
![Cont.
Definition: The probability density function (pdf) is an alternative
description of the probability of the random variable X: fX(x) = d/dx FX(x)
P[x1 ≤ X ≤ x2] = P[X ≤ x2] - P[X ≤ x1]
= FX(x2) - FX(x1)
= fX(x)dx over the interval [x1,x2]](https://image.slidesharecdn.com/chapter-4combined-230707191204-768bd611/85/Chapter-4-combined-pptx-12-320.jpg)