Download as PPS, PPTX
![[6]-20
=
′
′
−
=
′
′
=
′
′
1100
00
00
1
1100
0cossin
0sincos
1
1100
10
01
1
y
x
s
s
y
x
y
x
y
x
y
x
t
t
y
x
y
x
y
x
θθ
θθ
Translation
P’=TP
Rotation [O]
P’=RP
Scaling
P’=SP
Basic Transformations
Homogeneous Coordinates
Dheeraj S Sadawarte
https://dheerajsadawarte.blogspot.com](https://image.slidesharecdn.com/3overviewoftransformation-190810130855/85/Overview-of-2D-and-3D-Transformation-20-320.jpg)
Uploaded byDheeraj Sadawarte
Overview of 2D and 3D Transformation
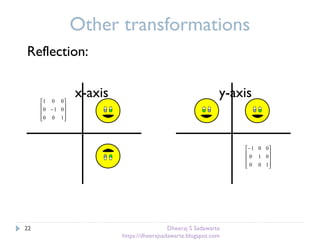
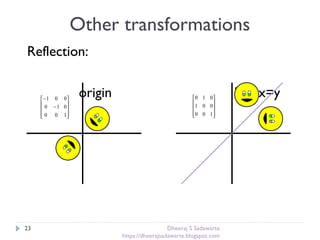
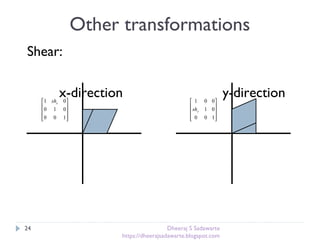
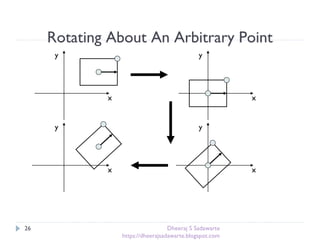
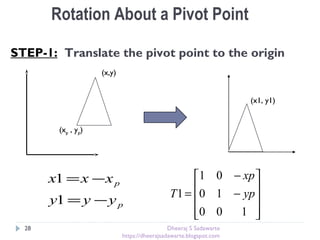
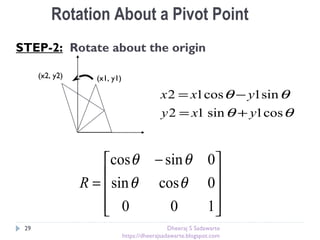
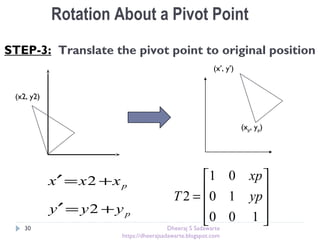
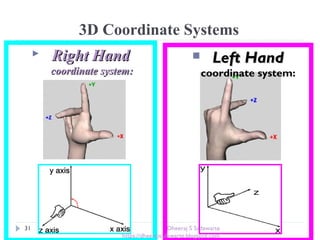
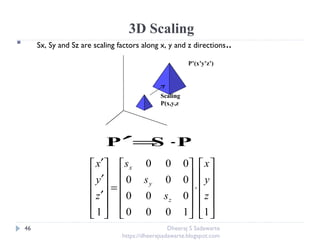
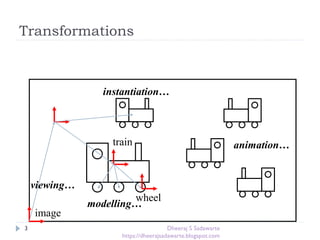
The document provides an overview of transformations in computer graphics, including translation, rotation, and scaling. It explains how these transformations modify the appearance and position of objects in 2D and 3D spaces, along with mathematical representations such as matrices. Additional transformations like reflection and shear are also briefly discussed.
More Related Content
Similar to Overview of 2D and 3D Transformation
Overview of 2D and 3D Transformation
- 1. Overview of Transformation DheerajS Sadawarte https://dheerajsadawarte.blogspot.com 1 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 2. Transformation 2 Transformation changesthe way object appears. Implementing changes in size of object, its position on screen or its orientation called Transformation. Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 3.
- 4. Basic 2D Transformation 4 Translation Scaling Rotation Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 5. Translation 5 Translation isa process of changing the position of an object in a straight line path from one coordinate location to another. Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 6. Translation 6 Dheeraj SSadawarte https://dheerajsadawarte.blogspot.com
- 7. Translation 7 Translate over vector(tx, ty) x’=x+ tx, y’=y+ ty or x y P P+T T = = = += y x t t y x y x TPP TPP' and, ' ' ' with, Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 8. Translation 8 A translationmoves all points in an object along the same straight-line path to new positions. The path is represented by a vector, called the translation or shift vector. We can write the components: p'x = px + tx p'y = py + ty or in matrix form: P' = P + T tx ty x’ y’ x y tx ty = + (2, 2) = 6 =4 ? Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 9. Translation polygon 9 Translate polygon: Applythe same operation on all points. Works always, for all transformations of objects defined as a set of points. x y T Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 10. Exercise 10 Translate apolygon with coordinates A(2,5), B (7, 10), and C (10, 2) by 3 units in x direction and 4 units in y direction Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 11. Rotation 11 Rotation transformationreposition an object along a circular path in the xy plane. The rotation is performed with certain angle , known asθ rotation angle x = r cos ϕ y = r sin ϕ x’ = r cos (ϕ + θ) y’ = r sin (ϕ + θ)ᶲᶲ Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 12. Rotation 12 x’ = rcos (ϕ + θ) y’ = r sin (ϕ + θ) x’ = r cos ϕ cos θ – r sin ϕ sin θ - since cos (A+B) y’ = r cos ϕ sin θ + r sin ϕ cos θ - since sin (A+B) x’ = x cos θ – y sin θ y’ = x sin θ + y cos θ Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 13. Rotation 13 Dheeraj SSadawarte https://dheerajsadawarte.blogspot.com
- 14. Rotation 14 A rotationrepositions all points in an object along a circular path in the plane centered at the pivot point. First, we’ll assume the pivot is at the origin. θθ P P’ Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 15. Rotation • Review Trigonometry =>cos φ = x/r , sin φ= y/r • x = r. cos φ, y = r.sin φ θθ φ P(x,y) x y r x’ y’ θθ P’(x’, y’) r => cos (φ+ θθ) = x’/r •x’ = r. cos (φ+ θθ) •x’ = r.cosφcosθθ -r.sinφsinθθ •x’ = x.cos θθ – y.sin θθ =>sin (φ+ θθ) = y’/r y’ = r. sin (φ+ θθ) •y’ = r.cosφsinθθ + r.sinφcosθθ •y’ = x.sin θθ + y.cos θθ Identity of Trigonometry 15 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 16. Rotation • We canwrite theWe can write the components:components: pp''xx == ppxx coscos θθ –– ppyy sinsin θθ pp''yy == ppxx sinsin θθ ++ ppyy coscos θθ • or in matrix form:or in matrix form: PP'' == RR •• PP ∀ θ can becan be clockwise (-ve)clockwise (-ve) oror counterclockwisecounterclockwise (+ve as our(+ve as our example).example). • Rotation matrixRotation matrix θθ P(x,y) φ x y r x’ y’ θθ P’(x’, y’) − = θθ θθ cossin sincos R 16 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 17. Scaling • Scaling changesthe size of an object and involves two scale factors, Sx and Sy for the x- and y- coordinates respectively. • Scales are about the origin. • We can write the components: p'x = sx • px p'y = sy • py or in matrix form: P' = S • P Scale matrix as: = y x s s S 0 0 P P’ 17 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 18. Scaling• If thescale factors are in between 0 and 1 the points will be moved closer to the origin the object will be smaller. P(2, 5) P’ • Example : •P(2, 5), Sx = 0.5, Sy = 0.5 •Find P’ ? •If the scale factors are larger than 1 the points will be moved away from the origin the object will be larger. P’ • Example : •P(2, 5), Sx = 2, Sy = 2 •Find P’ ? 18 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 19. Scaling • If thescale factors are the same, Sx = Sy uniform scaling • Only change in size (as previous example) P(1, 2) P’ •If Sx ≠ Sy differential scaling. •Change in size and shape •Example : square rectangle •P(1, 3), Sx = 2, Sy = 5 , P’ ? 19 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
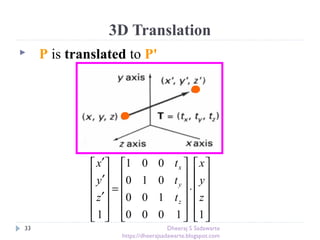
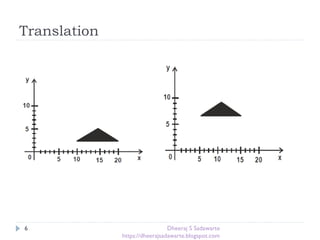
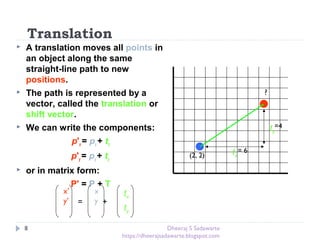
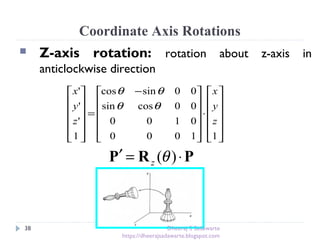
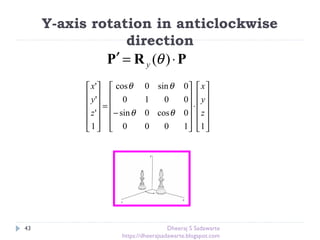
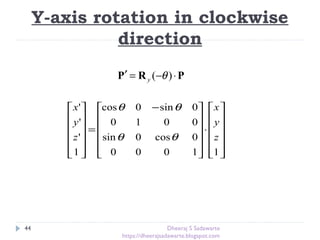
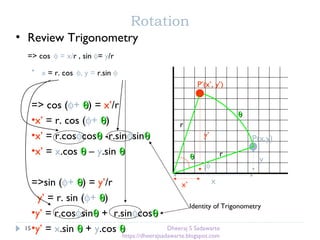
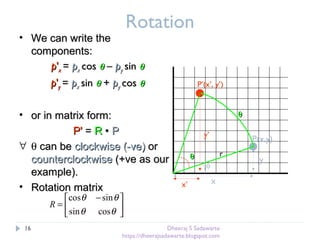
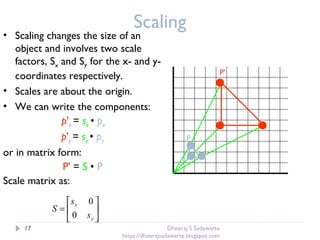
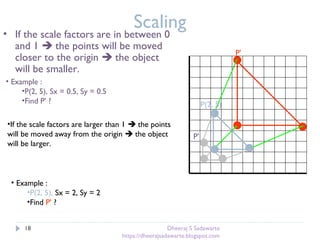
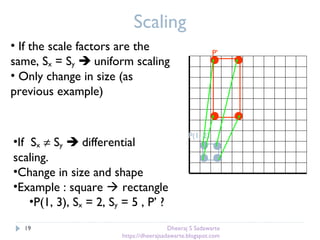
- 20. [6]-20 = ′ ′ − = ′ ′ = ′ ′ 1100 00 00 1 1100 0cossin 0sincos 1 1100 10 01 1 y x s s y x y x y x y x t t y x y x y x θθ θθ Translation P’=TP Rotation [O] P’=RP Scaling P’=SP BasicTransformations Homogeneous Coordinates Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 21. Other Transformation 21 Reflection Produces a mirror image of an object relative to an axis of reflection. Shear A transformation that slants the shape of an object is called the shear transformation X Shear preserves y coordinates but changes x values Y Shear preserves x coordinates but changes y values Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 22. Other transformations Reflection: x-axis y-axis − 100 010 001 − 100 010 001 22Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 23. Other transformations Reflection: origin linex=y − − 100 010 001 100 001 010 23 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 24. Other transformations Shear: x-direction y-direction 100 010 01xsh 100 01 001 ysh 24 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 25. Rotating About AnArbitrary Point 25 What happens when you apply a rotation transformation to an object that is not at the origin? Solution: Translate the center of rotation to the origin Rotate the object Translate back to the original location Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 26. Rotating About AnArbitrary Point x y x y x y x y 26 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 27. 27 (xp , yp) (x,y)(x’,y’) PivotPoint •Pivot point is the point of rotation •Pivot point need not necessarily be on the object Rotation About a Pivot Point Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 28. (xp , yp) p p yyy xxx −= −= 1 1 (x,y) (x1,y1) STEP-1: Translate the pivot point to the origin Rotation About a Pivot Point − − = 100 10 01 1 yp xp T 28 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 29. θθ θθ cos1sin12 sin1cos12 yxy yxx += −= (x1, y1) STEP-2: Rotateabout the origin (x2, y2) Rotation About a Pivot Point − = 100 0cossin 0sincos θθ θθ R 29 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 30. p p yyy xxx +=′ +=′ 2 2 STEP-3: Translate thepivot point to original position (x2, y2) (xp, yp) (x’, y’) Rotation About a Pivot Point = 100 10 01 2 yp xp T 30 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 31. 3D Coordinate Systems Right HandRight Hand coordinate system:coordinate system: 31 Left HandLeft Hand coordinate system: Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 32. 3 D Translation 32 In translation, an object is displaced and direction from its original position. The new object point p’=(x’,z’,z’) can be found by applying the transform Ttx,ty,tz to p=(x,y,z) Here tx=distance moved by object along x-axis ty=distance moved by object along y-axis tz=distance moved by object along z-axis Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 33. 3D Translation Pis translated to P' by: 33 PTP ⋅=′ ⋅ = ′ ′ ′ 11000 100 010 001 1 z y x t t t z y x z y x Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 34. 3D Translation AnObject represented as a set of polygon surfaces, is translated by translate each vertex of each surface and redraw the polygon facets in the new position. 34 ( )zyx tttT ,,= ( )zyx ,, ( )',',' zyx Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 35. 3D Rotation 35 Ingeneral, rotations are specified by a rotation axis and an angle. In two-dimensions there is only one choice of a rotation axis that leaves points in the plane. Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 36. 3D Rotation 36 Theeasiest rotation axes are those that parallel to the coordinate axis. Positive rotation angles produce counterclockwise rotations about a coordinate axis, if we are looking along the positive half of the axis toward the coordinate origin. Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 37. 37 Coordinate Axis Rotations Dheeraj SSadawarte https://dheerajsadawarte.blogspot.com
- 38. Coordinate Axis Rotations 38 Z-axis rotation: rotation about z-axis in anticlockwise direction ⋅ − = 11000 0100 00cossin 00sincos 1 ' ' ' z y x z y x θθ θθ PRP ⋅=′ )(θz Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 39. Rotation About Z-axisIn Clockwise direction. 39 Note that the +ve values of rotation angle Ө will produce a rotation in the anticlockwise direction whereas –ve values of Ө produce a rotation in the clockwise direction. in this case angle Ө is taken as –ve. According to the trigonometric law cos(Ө)= cos Ө sin(- Ө)= -sin Ө Now the matrix become ⋅ − = 11000 0100 00cossin 00sincos 1 ' ' ' z y x z y x θθ θθ PRP ⋅−=′ )( θz Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 40. Coordinate Axis Rotations 40 Obtain rotations around other axes through cyclic permutation of coordinate parameters: xzyx →→→ Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 41. X-axis rotation inanticlockwise direction: ⋅ − = 11000 0cossin0 0sincos0 0001 1 ' ' ' z y x z y x θθ θθ PRP ⋅=′ )(θx 41 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 42. X-axis rotation inanticlockwise direction: 42 ⋅ − = 11000 0cossin0 0sincos0 0001 1 ' ' ' z y x z y x θθ θθ PRP ⋅=′ )(θx X-axis rotation in clockwise direction: In this case angle Ө is taken as –ve. According to the trigonometric law cos(Ө)= cos sin(- Ө)= -sin Ө ⋅ − = 11000 0cossin0 0sincos0 0001 1 ' ' ' z y x z y x θθ θθ PRP ⋅−=′ )( θx Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 43. Y-axis rotation inanticlockwise direction ⋅ − = 11000 0cos0sin 0010 0sin0cos 1 ' ' ' z y x z y x θθ θθ PRP ⋅=′ )(θy 43 Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 44. Y-axis rotation inclockwise direction 44 PRP ⋅−=′ )( θy ⋅ − = 11000 0cos0sin 0010 0sin0cos 1 ' ' ' z y x z y x θθ θθ Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 45. Scaling Transformation 45 Ascaling transformation alters the size of an object. An object can be scaled (stretched or shrunk) along the x, y and z axis by multiplying all its points by the scale factors Sx, Sy, Sz All points P(x, y, z) on the scaled shape will now become P’(x’, y’, z’). Such that x’=x.Sx y’=y,Sy z’=z.Sz Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 46. 3D Scaling 46 Sx, Syand Sz are scaling factors along x, y and z directions.. ⋅ = ′ ′ ′ 11000 000 000 000 1 z y x s s s z y x z y x PSP ⋅=′ Scaling P(x,y,z P’(x’y’z’) Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 47. Scaling Transformation 47 Ifvalues of Sx, Sy and Sz<1 then size of objects reduced or the object move closer to the coordinate origin. If values of Sx, Sy and Sz>1 then size of objects increased or the object move farther to the coordinate origin. Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 48. Projections 48 Transform 3Dobjects on to a 2D plane 2 types of projections Perspective Parallel In parallel projection, coordinate positions are transformed to the view plane along parallel lines. In perspective projection, object position are transformed to the view plane along lines that come together to a point called projection reference point Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 49. Parallel Projection 49 Zcoordinate is discarded. Parallel lines from each vertex on the object are extended until they intersect the view plane. The point of intersection is the projection of vertex. Projected vertices are connected by line segments to correspond connection on original object. Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.com
- 50. Parallel Projection 50 DheerajS Sadawarte https://dheerajsadawarte.blogspot.comDheeraj S Sadawarte
- 51. Perspective Projection 51 Producesrealistic views but does not preserves relative proportions. Lines of projection are not parallel. Instead they all converge at single point called projection reference point. Dheeraj S Sadawarte https://dheerajsadawarte.blogspot.comDheeraj S Sadawarte
- 52. Perspective Projection 52 DheerajS Sadawarte https://dheerajsadawarte.blogspot.com