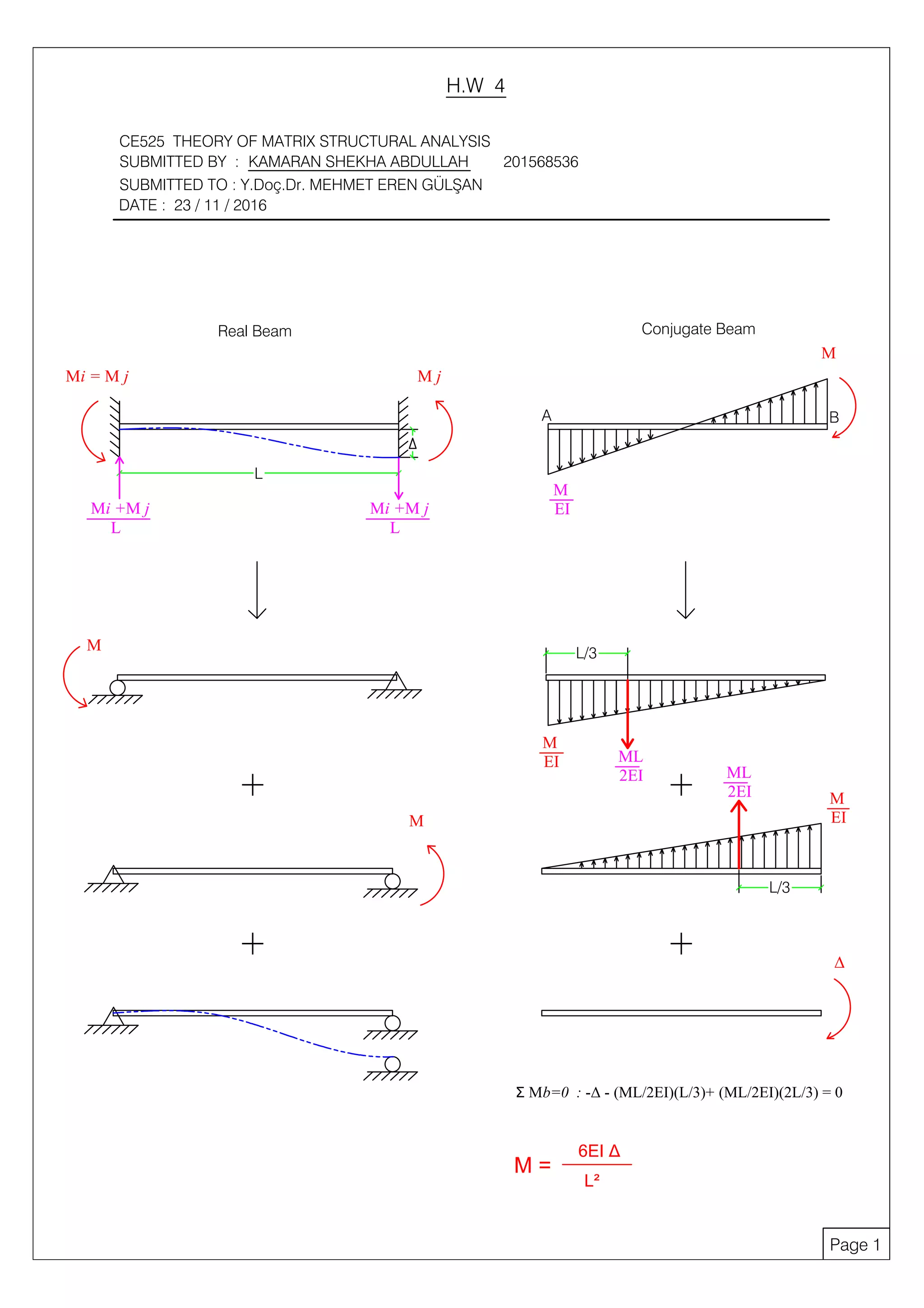
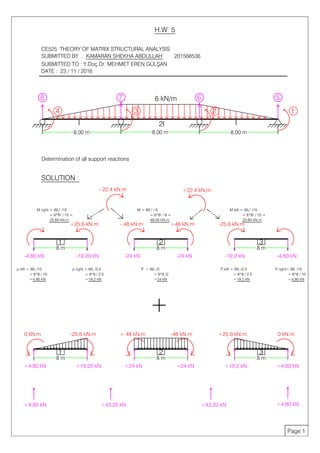
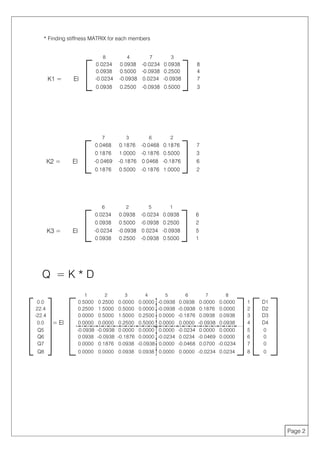
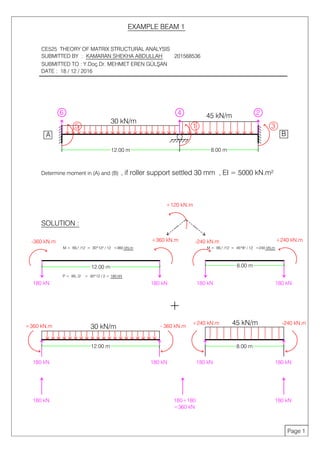
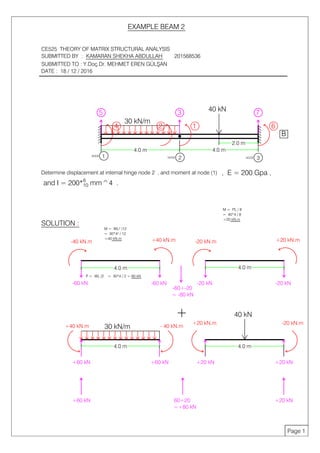
The document contains solutions to structural analysis problems involving beams. The first problem determines the support reactions of a beam with a distributed load. It involves finding the stiffness matrix, displacements, internal forces, and calculating the final reactions. The second problem calculates the moment at specific nodes for a beam with an internal hinge and applied point loads. It also finds the displacement at the hinge node using the stiffness matrix and equations for internal forces. The third problem similarly analyzes another beam, determining the moment at a node and displacement at the hinge location.

1. H.W 4
CE525 THEORY OF MATRIX STRUCTURAL ANALYSIS
SUBMITTED BY : KAMARAN SHEKHA ABDULLAH 201568536
DATE : 23 / 11 / 2016
Page 1
L
Mi = M j M j
Mi +M j
L
Mi +M j
L
M
M
+
+
M
A B
M
EI
M
EI
M
EI
+
+
ML
2EI ML
2EI
Mb=0 : (ML/2EI)(L/3)+ (ML/2EI)(2L/3) = 0
M =
L/3
L/3
Real Beam Conjugate Beam

2. 8.00 m8.00 m8.00 m
H.W 5
CE525 THEORY OF MATRIX STRUCTURAL ANALYSIS
SUBMITTED BY : KAMARAN SHEKHA ABDULLAH 201568536
DATE : 23 / 11 / 2016
Determination of all support reactions
SOLUTION :
6 kN/m
I 2I I
1
5
2
6
3
7
4
8
1
Page 1
25.60 kN.m
-4.80 kN -19.20 kN
+25.6 kN.m
3
25.60 kN.m
-19.2 kN -4.80 kN
-25.6 kN.m
2
48.00 kN.m
-24 kN -24 kN
+48 kN.m- 48 kN.m
8 m 8 m 8 m
+
1
+4.80 kN +19.20 kN
-25.6 kN.m
3
+19.2 kN +4.80 kN
+25.6 kN.m
2
+24 kN +24 kN
-48 kN.m+ 48 kN.m
8 m 8 m 8 m
0 kN.m0 kN.m
+4.80 kN +43.20 kN +43.20 kN +4.80 kN
- 22.4 kN.m +22.4 kN.m
p left = WL /10
= 6*8 / 10
=4.80 kN
p right = WL /2.5
= 6*8 / 2.5
=19.2 kN
P = WL /2
= 6*8 /2
=24 kN
P left = WL /2.5
= 6*8 / 2.5
=19.2 kN
P right= WL /10
= 6*8 / 10
=4.80 kN

3. * Finding stiffness MATRIX for each members
Q = K * D
Page 2

4. 0/EI = 0.5 D1 + 0.25 D2 + 0 D3 + 0 D4
22.4/EI = 0.25 D1 + 1.5 D2 + 0.5 D3 + 0 D4
-22.4/EI = 0 D1 + 0.5 D2 + 1.5 D3 + 0.25 D4
0/EI = 0 D1 + 0 D2 + 0.25 D3 + 0.50 D4
WE FIND THAT :
D1 = -12.8/ EI rad.
D2 = 25.6 / EI rad.
D3= -25.6 / EI rad.
D4= 12.8 / EI rad.
After that we find the (Q)
Q5 = {(-0.0938)(-12.8)}+{(-0.0938)(25.6)}
Q5 = -1.2 kN
Q6 = {(0.0938)(-12.8)}+{(-0.0938)(25.6)}+{(-0.1876)(-25.6)}
Q6 = 1.2 kN
Q7 = {0}+{(0.1876)(25.6)}+{(0.0938)(-25.6)}+{(-0.0938)(12.8)}
Q7 = 1.2 kN
Q8 = {(0.0938)(-25.6)}+{(-0.0938)(12.8)}
Q5 = -1.2 kN
Finally find the reactions
R5 = +4.80 +( -1.20 ) = 3.60 kN
R6 = +43.20 +( 1.20) = 44.40 kN
R7 = +43.20 + (1.20) = 44.40 kN
R8 = +4.80 +( -1.2) = 3.60 kN
Page 3

5. EXAMPLE BEAM 1
CE525 THEORY OF MATRIX STRUCTURAL ANALYSIS
SUBMITTED BY : KAMARAN SHEKHA ABDULLAH 201568536
DATE : 18 / 12 / 2016
Page 1
12.00 m 8.00 m
A B
Determine moment in (A) and (B)
SOLUTION :
30 kN/m
45 kN/m
kN.m
+360 kN.m-360 kN.m -240 kN.m +240 kN.m
kN.m
P = WL /2 = 30*12 / 2 = 180 kN
180 kN 180 kN 180 kN 180 kN
+
30 kN/m - 360 kN.m+360 kN.m
180 kN 180 kN
+240 kN.m -240 kN.m
180 kN 180 kN
8.00 m12.00 m
12.00 m 8.00 m
1
4 26
35
180 kN 180+180
=360 kN
180 kN
45 kN/m
+120 kN.m

6. Page 2
Q = K + D
K = K1 + K2

7. 120 = 4166.667 D1 + 260.417 * -0.03
Page 3
D1 = 0.03067 rad
* Now we find out Q3 and Q 5
Q3 = {1250 * 0.03067 }+{468.75* -0.03 }
Q3 = 24.275 kn.m
Q5 = {833.33 * 0.03067 }+{-208.33* -0.03 }
Q5 = 31.8081 kn.m
* finally we find out M3 and M 5
M3 = - 240 + 24.275 kn.m
= - 215.73 kN.m Ans.
M5 = +360 +31.8081
= 391.81 kN.m Ans.
* Also we can find out reactions :
Q2 = {-468.75* 0.03067 }+{-117.88* -0.03 }
Q2 = -10.84 kN
Q4 = {260.417* 0.03067 }+{151.91* -0.03 }
Q4 = 3.43 kN
Q6 = {208.33* 0.03067 }+{-34.722* -0.03 }
Q6 = 7.43 kN
Reactions :
R2 = 180 + (-10.84)
= 169.16 kN
R4 = 360 + (+3.43 )
= 363.43 kN
R6 = 180 + (+7.43)
= 187.43 kN

8. EXAMPLE BEAM 2
CE525 THEORY OF MATRIX STRUCTURAL ANALYSIS
SUBMITTED BY : KAMARAN SHEKHA ABDULLAH 201568536
DATE : 18 / 12 / 2016
Page 1
4.0 m 4.0 m
B
Determine displacement at internal hinge node 2 , and moment at node (1) , E = 200 Gpa ,
and I = 200*6
10 mm^4 .
SOLUTION :
30 kN/m
=40 kN.m
+40 kN.m-40 kN.m -20 kN.m +20 kN.m
M = PL / 8
= 40*4 / 8
=20 kN.m
P = WL /2 = 30*4 / 2 = 60 kN
-60 kN -60 kN -20 kN -20 kN
+
30 kN/m - 40 kN.m+40 kN.m
+60 kN +60 kN
+20 kN.m -20 kN.m
+20 kN +20 kN
4.0 m4.0 m
4.0 m
1
3 75
64
+60 kN 60+20
=+80 kN
+20 kN
2
40 kN
4.0 m
2.0 m
40 kN
-60+-20
= -80 kN
1NODE
2NODE 3NODE

9. Page 2
Q = K * D

10. -20 = 40,000 D1 + 0,0 D2 +15,000 D3
+40 = 0.0 D1 + 40,000 D2 + -15,000 D3
-80 = 15,000 D1 + -15,0 D2 +15,000 D3
Page 3
D1 = +0.005249 rad Ans.
* Now we find out Q4
Q4 = {0 * 0.00475 }+{20,000* -0.00475 } +{-15,000 * -0.01533}
Q4 =+134.95 kN .m
* finally we find out M4
M4 = + 134.95 + 40
= + 174.95 kN.m Ans.
D2 = - 0.00475 rad Ans.
D3 = - 0.01533 m Ans.