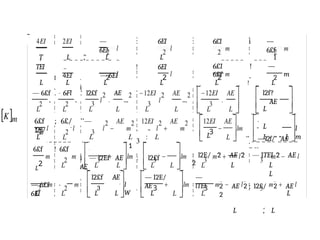
The document presents a detailed analysis of the stiffness method applied to beams and frames in structural engineering. It outlines the derivation of member stiffness matrices for various loading conditions, including shear forces and bending moments, using a combination of equations and diagrams. Key concepts such as transformation matrices and relationships between local and global coordinates are emphasized for understanding and applying structural analysis techniques.

1. PRIYADARSHINI COLLEGE OF ENGINEERING, NAGPUR
PRESENTATION ON
MATRIX ANALYSIS OF STRUCTURE
SUBMITTED BY
Mr. BRIJESH FULSINGH THAKUR CHAUHAN
MTECH – 1ST
YEAR (1st
SEMESTER)
STRUCTURAL ENGINEERING
SUBJECT
ADVANCED CONCRETE STRUCTURAL DESIGN
FACULTY INCHARGE
PROF. PRANITA BHANDARI MA’AM

2. 4.1 INJ“ROI1UCJ’ION:
In chapter 3 the analysis of trusses using stiffness method was
discussed. In this chapter application of stiffness method will be extended
to beams and place frames. The procedure for application of this method
is the same as that of the trusses but the difference is only in member
stiffness matrix and deformation transformation matrix, which will be
developed in the subsequent section.
4.2 MEMDER OR ELEMENT STIFFNESS MATITIX (FI EXURAL
ELEMENT ):
As a frame element is subjected not only to axial forces but also to
shear forces and bending moments, therefore three degrees of freedom per
joint of a frame element are present. A degree of freedom is an
independent deformation of a joint or a node. These are:
i Axial delormation.
ii) End rotations.
iii) Normal translations.

3. Out of these three, axial deformation is normally neglected, so element or
member stiffness matrix for an element subjected to shear force and
bending moment will only be developed at this stage.
Flgure 4.1
’
3
Frame element after the application of
load
Prame element before the application of load

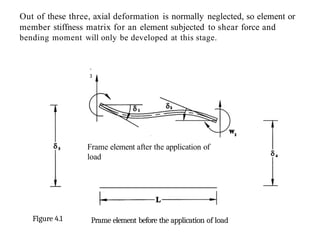
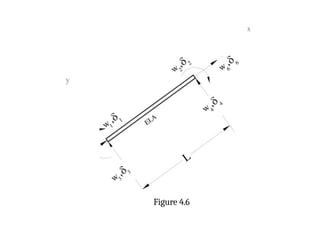
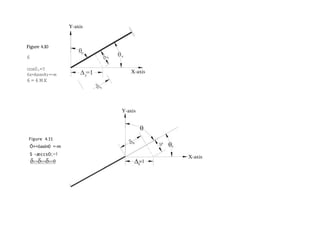
4. Consider a member/element shown in figure 4.1. The x-y coordinate system
shown is local coordinate system. Origin is always at the near end. There
are two forces (shear force w3 and a moment w1) acting at near end of the
joint and correspondingly there are two deformations (vertical translations
63, and rotation 81).Similarly there are two forces (shear force w4 and a
moment w2) acting at the far end of the joint and correspondingly two
deformations (vertical translation fi4 and rotation 62).
4.2.1 SIGN CONVFNTION
Moments (wI, w2) and rotatioiis (II and H) are positive
ivheii clockWfSC ffltd negative wlten counter clockwise.
Translation fi3, 64 are positive w/ten npwnrd and negative when
downward. The local x-axis runs along the member from the first joint to
the second joint
4.2.2 DERIVATION
The load-stiffness-deformation relationship for this element is the same as
that for a truss element as expressed in equation 3.17.
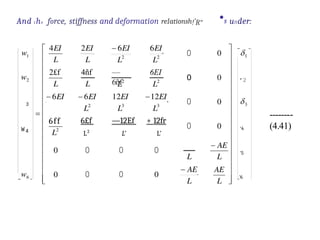
[w]q, = [k]„, [6]„,.--------------------------------- (3.17)
As there are four forces and four corresponding deformations then the
equation 3.17 can be expanded in the following form:

5. k, k k,
---------------------------------- (4.1)
Where each element of the stiffness matriE is called stiffness coefficient
as discussed in chapter 2. It represents the place occupied by it with
respect to row and columns. Any stiffness coefficient may be represented
by kij; where i and j are number of rows and columns.
The above mentioned element stiffness matrix [k]m is formed by
applying a unit value of each end deformation in turn and the
corresponding column of the matrix of equation 4.1 gives the various end
forces developed at the member ends while other deformations are
restrained. This procedure is as follows:
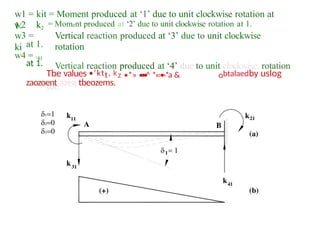
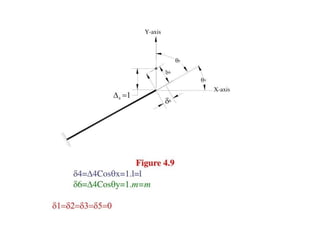
Apply unit positive deformation (clockwise rotation) ôl = 1 and
equating all other deformations to zero (ö2 = fi3 = 64 = 0). The element
would be deformed as shown in figure 4.2.a. From the definition of
stiffness, the forces induced at hoth ends due to unit clockwise rotation of
near end are as under.

6. w1 = kit = Moment produced at ‘1’ due to unit clockwise rotation at
1.
w2 k2
w3 =
ki at 1.
w4 = ‘41
= Moment produced at ‘2’ due to unit clockwise rotation at 1.
Vertical reaction produced at ‘3’ due to unit clockwise
rotation
Vertical reaction produced at ‘4’ due to unit clockwise. rotation
at 1.
Tbe values •’ktt, kz •*» •
•
•
^ *«›•›*a & obtalaedby uslog
tbe.
zaozoent azea tbeozems.

7. Figure 4.2
As according to moment area theorem no.1 change in slope between two
points on an elastic curve is equal to area of the M/EI diagram between
these two points. Looking at figure 4.2’a’ change in slope between two ends
is equal to unity. Adding the areas of figure 4.2 (b) and figure 4.2 (c).
k 21
kl
1
_ k21 = i .0 ------------------------------
(•4•2)
2/11 27fI

8. According to theorem no.2 of moment area method tangential deviation
of a certain point with respect to the tangent at another point is equal to
the moment of M/EI diagram between the two points calculated about
the point where the deviation is to be determined. From the above
definition the moment of M/EI diagram (figures 4.2 (b) and 4.2 (c) )
about the left of the member is equal to zero.
kl1’* k2l’L
L
2L
2EI 3 2A/ 3
—
—
o
(4.3)
Following values of k 1 and k2 are obtained by solving equations 4.2 and 4.3.
J 4J/
2E/
L
"""""""-"""----------------(4.4)
2
1
Reaction kg1 and k„ can be obtaineil using ct uutitin tif equilibrium.
Summation of moments about the right end is equal to zero (see iigure
4.2 (d).

9. ZMB=0
k;, L -
k„ - k
= &--------------------------------- (4.5)
’’ ' + 2£ -- --------------- (4.6)
L
''31
k31
L + 2€/ /
L
(4.7)
^RR!y••8:tO••e Equation of equilibrium to figure 4.2 (d)
ZFy = 0
k4 - k3 0
k4 = k
p
(4.8)
k41
6£/
L
2
(4.9)

10. These are the forces and moments as shown in figure 4.2 a, b, c, d. On
comparison with figure 4.1 the correct signs are obtained and these are
defined by the following equations.
4EI
L k21
k41
2EI
L
2
This gives the first column of the element stiffness matrix. As this
matrix is symmetric so it also provides the first row. To obtain 2nd
column of stiffness matrix deformation (rotation) fi2 = 1 is imposed on
the far end equating all other deformations to zero fi1 = 63 = 64 = 0.
The element would be deformed as shown in figure 4.3 (a). From
the
definition of stiffness as mentioned in chapter 2, the forces induced at
both ends due to unit rotation at far end can be defined as

11. wI = k12 = Moment produced at
‘1’ due to unit clockwise
rotation at 2.
w2 = k22 = Moment produced
at
‘2’ due to unit
clockwise rotation at 2.
w3 = k32 = Vertical reaction
produced at ‘3’ due to unit
clockwise rotation at 2.
w4 = k42 = Vertical reaction
produced at ‘4’ due to
unit clockwise rotation at
2.
The values of k12, k22, k32 and
k42 can be obtained by
using the moment area
theorems.
(s)
- L -

12. 2€/
12
L
4EI
Applying moment area theorem no. 1 and using bending moment diagram of
figure 4.3 (b,c). For this case change in slope between both ends is equal to
unity so
(4.11)
2A/ 2€/
However according to moment area theorem no.2 the moment of
M/El
diagram about the right end of the member is equal to zero.
2)
Solving equations 4.11 and 4.12
22
L
""""""""""
""
---------- (4.13)
Reaction k and k,2 can lie ohtained using equation ol' equilibrium. Summation
of moments about the left end is equal to zero tsee figure 4.3 (d)).

13. Applying force equation of equilibrium to ftgure 4.3 (d)
-k32=O
ki2' 2
(4.15
)
These are the force s and moments as shown in figure 4.3 a, b, c, d. On comparison with
figure 4.1 the correct signs are obtained and these are defined by the following equations

14. , k32'
‘
6EI
2 2 17
)
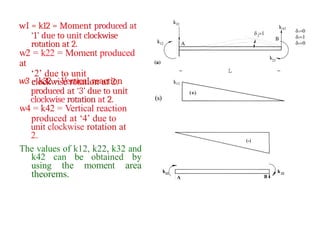
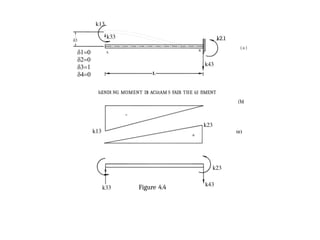
Continuing this process of applying unit vertical translation 63 = 1 and solving
for forces and moments as shown in figure 4.4 (a, b, c, & I) and applying unit vertical
translation 34 = 1 and solving for forces and moments as shown in figure 4.5 (a, b, c & d),
third row., third column, fourth row and fourth column can be obtained.
Following is the
summary of the se calculations.
For 5s — I (see figure 4.4a) . change in slop e between both ends is zero.
Therefore
’]3 - ’13
=
2f/ 2 1
(418)
(4
19)

15. k2.1
(a)
hENDl NG MOMENT D1 ACiítAM S FAIR THE üI fiMENT
(bï
Figure 4.4

16. Moment of bending moment diagrams in figure 4 4b and 4 4c about left end is equal to
unity, therefore
k„£
2£
2E/
3
ku£
2F/ 3
2£ ''
2f/ 3 2S£
3
A (21'-I' - 1
2f/ 3
p
k
—-
6
EI

17. T akin_• moine iitx abont i ip•lit enil țser fkgiii e 4 4‹lì
ȚMø=0
12 NJ
§Fy=O
3=k
(4.24)
(4.25)
(4.26
)
t2Æ/
33 —
23 y2
—12J/
(4. 2T}

18. For the case when
therefore
34 = 1 (see figure 4.5a) change in slope between both ends is zero,
2£i 1 EI
4 = 4J
4.28)
Moment of bending moment diagrams (figure 4.5b, 4 5c) about right end is equal to unity,
therefore
(4.29)
- =
1

19. Substituting value of 2‹ from equation 4.
28.
Applying equation of moment equilibrium about left end (see figure 4.5d).
M4'k4+kg
0
)

20. Applying equation of force equüibrium to figure 4.5(d)
Fy = 0
L -
k
.
,
B
k
- L
Figure 4.5
-
1
k.•

21. 12Er ---------------------- (4.34)
L
3
Correct slgns can be obtained by comparing theae vnlues wtth figure
4.1. These are defined as
kl4'
L2
6E7
L
2 k34
—12EZ
L3
12A
f
------- (4.35)

22. L L L2
L’
— 6
ñ
/ — 6
ñ
/ l 2ñ/ I 2£/
L'
6€/
L’
6EI
L'
—
12€/
L’
12F/
_ L’ L
2
E’ E'
(4.36)
And the force, stiffness and deformation relationship is as under:-
L L L‘’
L2
2£/ 4£/ — 6Ef 6E/
L L
L‘’
— 6
ñ
/ — bEl
12A/
L‘’
12ñf
L
"
L
"
L’ L’
------------------------ -- (4.37)

23. 4.3 MEMBER OR ELEMENT STIFFNESS MATRIX FOR A BEAM /
FRAME ELEMENT SUBJECTED TO MOMENTS ONLY:
The element stiffness matrix for members whose ends cannot
translate but can rotate is obtained by removing third and fourth row
corresponding to fi3, 64 and third and fourth columns corresponding
to w3 and +4 from the above mentioned element stiffness matrix of
equation 4.36 as shown below:-
TEI + TEI — 1 2Ef I 2£f
The resulting stii“fness matrix for a lieam element is as follows:
EI 4
L
2
.38)

24. And the furce sti fitess deforinatimt relationship for a beam eleitteitt is as
follows:-
- (4.39)
4.4 MEMBER OR ELEMENT STIFFNESS MATRIX OF A FRAMF
ELENIENT SUBJECTED TO AXIAL I OADING IN ADDITION TO
SHEARING FORCES AND DENYING MOMF.NTS.
The fiiial element that is capable of axial lending in
nddition
tu shenr forces and bending moments is tie w considereJ.
The stiffness matrix for this element can be formed by
superposition of the element stiffness matrix of truss element and frame
element formed as given in the equations 2.16 and 4.20. Figure 4.6 defines the
positive forces (axial forces, shear forces and bending moments) and
deformations (axial deformations, vertical translations and rotations) for the
element.

25. Figure 4.6

26. L2 L2 L3
z3
0 0 0 0
0 0 0 0
4Ef
L
2Ef
L
—bEl
52
6Ef
¿,2
2Ef 4EZ —6€f 6Ef
L
—6£ł
L
—6Ff
¿,2
12£ż
52
—12Ei
L2
L2 L
3
L
'
z
0
0
0
0
_ L
(4.40)

27. And t he force, stiffness and deformation reIationsh!’R“ •s uflder:
3
2£f 4ñf —
6ñf
6EI
W 4
6ff 6£f —12Ef + 12fr
L2
L’ L’
0 0 0
0 0
0
0
0
0
’2
‘4
‘5
_‘6
--------
(4.41)

28. 4.5 DEFf)RMATION TRANSFtJRMATIf)N MATRIX:
As discussed in the case of trusses, deformation transformation matrix is
used to transform the element deformations from local coordinates to
structure deformations in global co-ordinates. Using this deformation
transformation matrix structure stiffness matrix is obtained as given in
the following equation:
4.5.1 DLI ORA1A'1 ION '1 RANS£ OR.MA'1’ION MA'1 RIX OF A FRA.HE
ELEMENT SUB,IECTED Tt) AXIAL Ft)RCE, SHEAR Ft)RCE
AND BENDING MOMENT.
A deformation transformation matrix will also be developed to carry out
the transformation from element to global coordinates.
Consider the frame member shown in figure 4.7. Member axis, x-
axis of member coordinate system makes an angle 8x with x-axis of the
structure coordinate system as shown in figure 4.7 (b), similarly
member axis, x-axis of member coordinate system makes angle 8y with
y-axis of the structure coordinate system. The cosines of' these angles
are given below
1= Cos 8x

29. Element forces and
deformations
Mguœ47
Structure forces and deformations

30. A gain consider the frame member shown in figure 4.7, d and d2 are the
element deformations (rotation) whereas D and A2 are the structure
deformations (rotations). As Z-axes for both element and strucmre
coincides, therefore both element and strucmre rotations will be the same
when structure deformation At = 1, then the element deformation
d, l
’2
#,
'
= 0
‘4 0
(4.43)
and when structure deformation A2 = 1, then the element deformations
6 =
0
d l
‹f3
0
d4
0
(4.44)

31. Relationship between structure and element deformations can also be
obtained in the similar manner for a unit vertical translation of the
left end i.e. A3 = 1 (see figure 4.8)
fi3 = A3.Cos 8x, 65 — A3.Cos
8y fi3 = 1. Cos 8x, 65 = 1. Cos
8y 63=1. 1 = , I 65=1.m=m
FIGURE 4.8
fi3=AWCos8
=1./N
6 =62' 4
6
6,
d2
0
0
84 =
0
' Y—
axis
(4.45)
X-axis

33. For a unit vertical translation of the right end i.e. A$ = 1 {Fig.4.9)
element deformations are as under:
‹I, =
0
J2
0
#5
0
(4.46)
where 6J and 6 are vertical translations of the element.
for a unit horizontal translation (along x-axis) of the lefLend-+yfig
1
element deformations are as under:-
.4.10)
’6
(4.47)

34. For a unit horizontal translation the right end I-e;A$= 1, element
deformatians are as under:-
‹11
0
ò2 =
0
‹f3 0
'
5
_
6
0
(4.48)

35. Figure 4.10
6
cos0.=?
6z=Assn8;=-m
6 = 6 M X
Figure 4.11
Ô+=óasin0 =-m
S -æccs0;=f

37. 0 0
1 0
0 I
0 0
This is the deformation transformation matrix of a frame element subjected
to shear force, bending moment and axial forces.
To obtaln the deformation transformation matrix of a beainfframe element
subjected oaly to shear force and bending moment, the axial deformations are
ignored. Therefore by deleting last two rows and last two columns of the matrix
in equation (4.50) following deformation transformation matrix is obtained:
T ——
(4.51)
Similarly to obtain the deformation transformation matrix of a beam/frame
element subjected only to bending moment, the axial and shear
deformations are ignored Therefore by deleting last two rows and last two
columns of the matrix in equation (4.51) following deforniadon
transformation matriz 1s obtained:
T
—
(4.52)

38. 4.6 iiTRUCTURE STIFFNESS MATRICEii
4.fi.1 For a lieam/l'rame element s«$iected to bending moment onlv:
Using the element stiffness matrix and deformation transformation matrix
structure stiffness matrix is formed. Following equation is used for this
purpose:
[K]„, = [T) „ [k] [T]„,
Where,
[T]. = Deformation Trait.sformation matrix
[k]. = Element stillness matrix
In this case:
An
d [k n
EI 4
2
L 2
4 1
0
0
(4.53)
(4.52)
(4.38)

39. L
-6EI
L
-6EI
L
2
12€J
L
2
—12r1
6ri
_ L2
6rf
L2
—12ri
L3
12ri
L3
EI 4
L
2
(4.54)
4.6.2 Beam/Frame element subiected to Shear Force and Bending Moment
onlv:
o o
1 0
0
I
0
0
(4.51)
(4.36)

40. — hEl —
6£/
12F
q/ — 12
£/
L‘’ ' L’ ' L’ ' L’ '
4E/ 2€f — h
Al
L L L"
T
T
,
0 (
)
1 0
0 1
0 0
Substituting these values in equation (4.53) the following structure stiffness
matrix is obtained:
L
"
L
2
2E/ 4E/ — EI
.1
6Ef
.1
L L
.
I
6E/
.
TEI — I
2EI
L’ L’
I 2EI
L’
_ L
‘’
(4.55)

41. L’ L L' E’
6EI 6fr - l2fr 12EI
o
0
o
0
o
0 0
Here
4.6.3 Frame element subjected to Shear Force/ Bending
Moment/Axial Forces:
00 0 0
10 0 0
0 0
—
0 0 1 0
0 m 0 1
0 0 m 0
4EI 2£/ — 6EI 66/
0 0
0 0
0 0
0
0
AE
AE
L
L
— AE AE
(4.50)
(4.40)

42. and
00 0 0 0
10 0 0 0
0 1 0 —m 0
0 0 f 0 —
m
0 m 0 / 0
0 0 m 0 /
Substituting these values in equation (4.53) and multiplying, structure stiffness
matrix is given on the next page, is obtained.

43. Ț
TEI
_L_ _ _','_ _ _ _L_ _
_
4EI — 6EI
I .
L
,
. i
L
— 6£f . - 6Fl .
' l2£f
2
L
. . .
—
6EI
: 6EI : 6£1 i —
6£f
!
L
6EI
L
2
AE
2
L
'
3
2
6£f ; 6£/ ''—
12£/ 3
m
_ _ _ _ _ _ _ _ 1
6£1 ! —
6£f
!' 2
L L
l2f?
AE
L
L
'' —12f/” ”A£
l
m
L L
6£f ! 6£f
L L : L
1
i — l2Ef AE : l2£f
AE
L
. - -- -- -- - -- -- -- --
-- --
: l2E/ 2 AE 2 — ITEI 2 AE
2
L
2
— 6£f -
6EI
L
l
W
3 .
L
l2£f AE
L
3
L
3
L L
L
2 AE 2 ; 12£/ 2 AE
2
L ,
' L
— I2E/
AE
—
lTEI
L