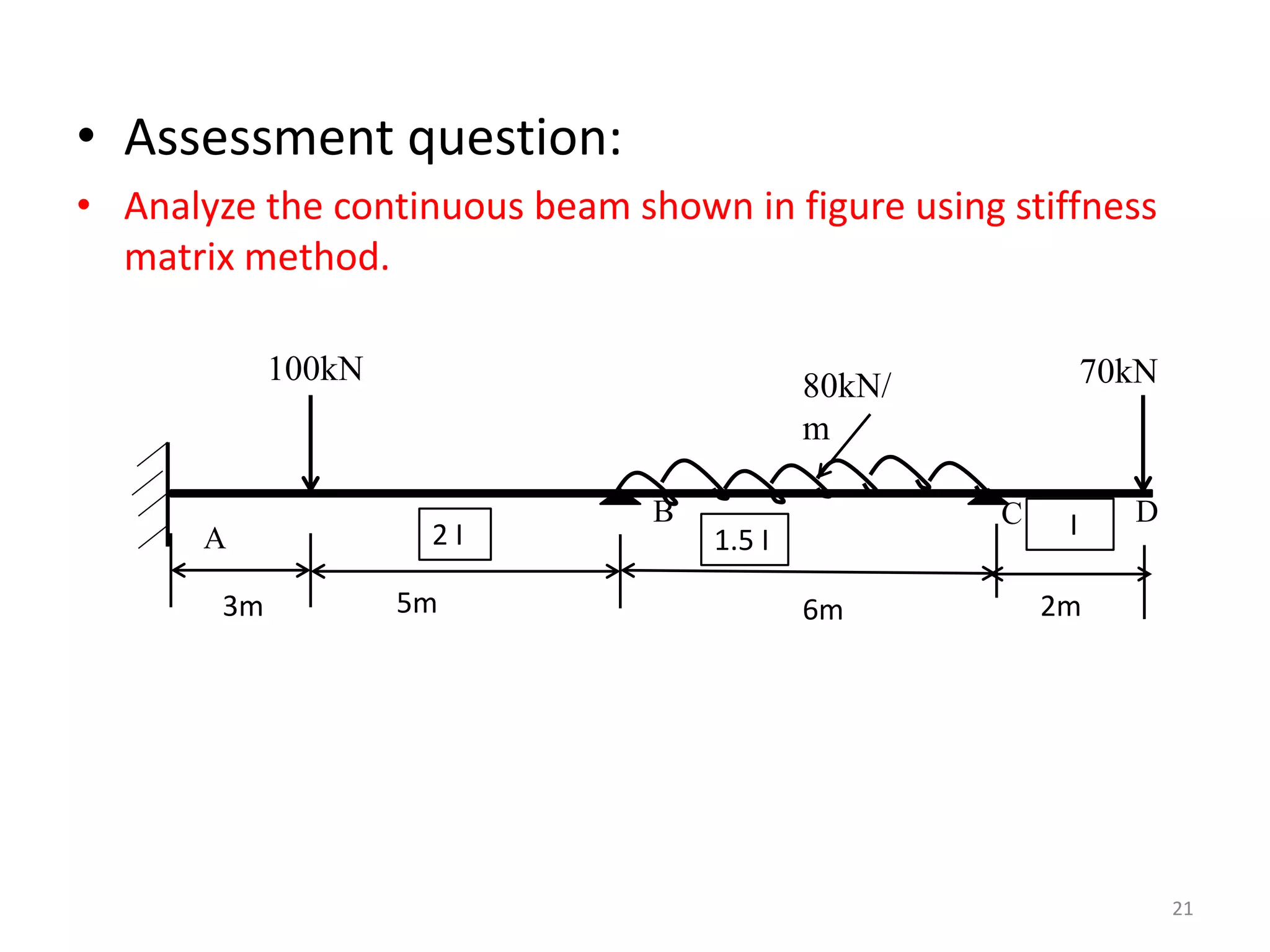
The document presents a detailed analysis of a continuous beam using the stiffness method, outlining the steps for determining degrees of freedom, calculating fixed end moments, and assembling the stiffness matrix. It includes calculations for forces at various coordinate numbers, leading to the determination of actual forces and final moments in the beam. The assessment question encourages further analysis of a different continuous beam using the same method.

1. Stiffness Method Problem
Dr. Kasi Rekha
B.Tech., M.Tech., Ph.D., MIE
1
Presented by

2. • Analyze the continuous beam shown in figure
using Stiffness method.
2
40 kN 60 kN 80 kN
A B C
D
2m 4m 2m4m 4m
2 I 1.5 I
60 kN 80 kN
B C
D
4m 2m4m 4m
2 I 1.5 I
80 kN-m

3. • Step1:
– Degree of Freedom or Kinematic Indeterminacy : 3
3
B C
D
4m 2m4m 4m
2 I 1.5 I
θb θc θd

4. 4
• Step 2:
– Assign Coordinate Numbers in the direction of degrees of
Freedom
B C
D
4m 2m4m 4m
2 I 1.5 I
1 2 3

5. 5
• Step 3:
– Restrain the structure at all coordinates
B C
D
4m 2m4m 4m
2 I 1.5 I
1 2 3

6. 6
• Step 4:
– Determination of Fixed End Moments
60 kN 80 kN
B C
D
4m 2m4m 4m
2 I 1.5 I

7. • 𝑀 𝐹
𝑏𝑐
= −
𝑤𝑎𝑏2
𝑙2 = −
60×4×42
82 = −60 𝑘𝑁 − 𝑚
• 𝑀 𝐹
𝑐𝑏
=
𝑤𝑎2 𝑏
𝑙2 =
60×4×42
82 = 60 𝑘𝑁 − 𝑚
• 𝑀 𝐹
𝑐𝑑
= −
𝑤𝑎𝑏2
𝑙2 = −
80×4×22
62 = −35.55 𝑘𝑁 − 𝑚
• 𝑀 𝐹
𝑑𝑐
=
𝑤𝑎2 𝑏
𝑙2 =
80×22×4
62 = 71.11𝑘𝑁 − 𝑚
7

8. • Step 5:
– Calculation of forces in co ordinate numbers
𝑃1𝑙 = 𝑀 𝐹
𝑏𝑐
= - 60 kN-m
𝑃2𝑙 = 𝑀 𝐹
𝑐𝑏
+ 𝑀 𝐹
𝑐𝑑
= 60-35.55= 24.45 kN-m
𝑃3𝑙 = 𝑀 𝐹
𝑑𝑐
= 71.11 kN-m
8
B C
D
4m 2m4m 4m
2 I 1.5 I
1 2 3

9. • Step 6:
– Assembly of Stiffness Matrix
i. Applying Unit Rotation in co ordinate direction 1
9
B C
D
4m 2m4m 4m
2 I 1.5 I
1 2 3
θb = 1 θc = 0 θd = 0

10. 10
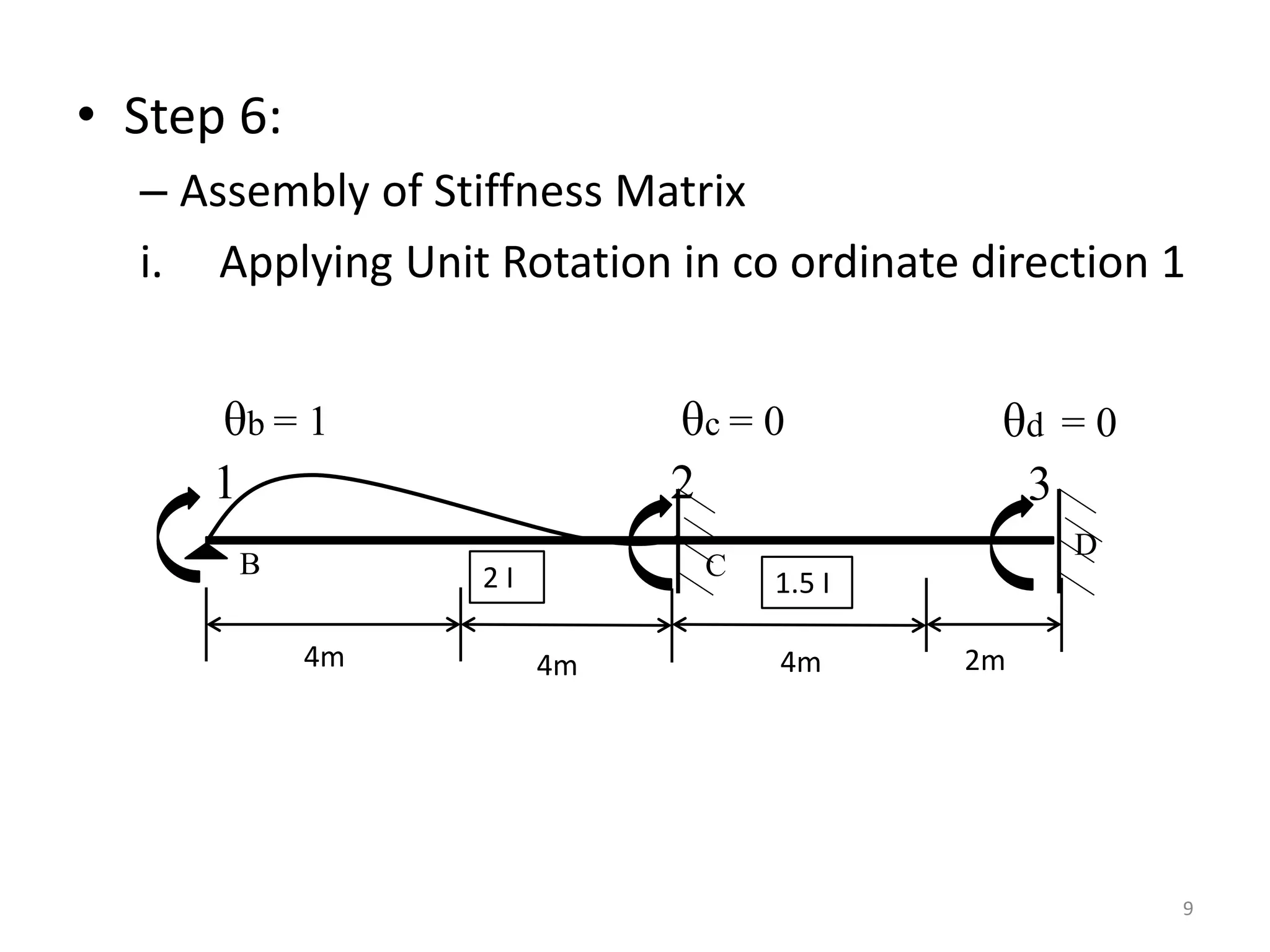
𝐾11 = 𝐾𝑏𝑐 =
2𝐸𝐼
𝐿
[2𝜃 𝑏 + 𝜃𝑐] =
2𝐸(2𝐼)
8
2 × 1 + 0 =EI
𝐾21 = 𝐾𝑐𝑏 =
2𝐸𝐼
𝐿
[2𝜃𝑐 + 𝜃 𝑏] =
2𝐸(2𝐼)
8
2 × 0 + 1 = 0.5 EI
𝐾31 = 0

11. 11
• Step 6:
– Assembly of Stiffness Matrix
ii. Applying Unit Rotation in co ordinate direction 2
8m 6m
θb = 0
1
2 3
2 I 1.5 I
θc = 1 θd = 0

12. 12
𝐾12 = 𝐾𝑏𝑐 =
2𝐸𝐼
𝐿
[2𝜃 𝑏 + 𝜃𝑐] =
2𝐸(2𝐼)
8
2 × 0 + 1 = 0.5EI
3𝐾22 = 𝐾𝑐𝑏 + 𝐾𝑐𝑑
=
2𝐸𝐼
𝐿 𝑐𝑏
[2𝜃𝑐 + 𝜃 𝑏] +
2𝐸𝐼
𝐿 𝑐𝑑
2𝜃𝑐 + 𝜃 𝑑
0 =
2𝐸(2𝐼)
8
2 × 1 + 0 +
2𝐸(1.5𝐼)
6
2 × 1 + 0 = 2𝐸𝐼
𝐾32 = 𝐾 𝑑𝑐 =
2𝐸𝐼
𝐿 𝑏𝑐
[2𝜃 𝑑 + 𝜃𝑐] =
2𝐸(1.5𝐼)
6
2 × 0 + 1 = 0.5EI

13. 13
• Step 6:
– Assembly of Stiffness Matrix
iii. Applying Unit Rotation in co ordinate direction 3
2 I 1.5 I
8m 6m
1
2 3
θb = 0
θc = 0 θd = 1

14. 14
0𝐾13 = 𝐾𝑏𝑐 = 0
3𝐾23 = 𝐾𝑐𝑑
=
2𝐸𝐼
𝐿 𝑏𝑐
2𝜃𝑐 + 𝜃 𝑑
0 =
2𝐸(1.5𝐼)
6
2 × 0 + 1 = 0.5𝐸𝐼
𝐾33 = 𝐾 𝑑𝑐 =
2𝐸𝐼
𝐿 𝑏𝑐
[2𝜃 𝑑 + 𝜃𝑐] =
2𝐸(1.5𝐼)
6
2 × 1 + 0 = EI

15. • GLOBAL STIFFNESS MATRIX
𝐾 =
𝐾11 𝐾12 𝐾13
𝐾21 𝐾22 𝐾23
𝐾31 𝐾32 𝐾33
= EI
1 0.5 0
0.5 2 0.5
0 0.5 1
15

16. • STEP7:
– Calculation of Actual Forces
𝑃 − 𝑃𝐿 =
𝑃1 − 𝑃1𝐿
𝑃2 − 𝑃2𝐿
𝑃3 − 𝑃3𝐿
=
−80 − (−60)
0 − 24.45
0 − 71.11
=
−20
−24.45
−71.11
16

17. 17
• GLOBAL STIFFNESS MATRIX
K Δ = P-𝑃𝐿
EI
1 0.5 0
0.5 2 0.5
0 0.5 1
Δ1
Δ2
Δ3
=
−20
−24.45
−71.11
Δ1 + 0.5 Δ2 = -20
0.5 Δ1 + 2 Δ2 + 0.5 Δ3 = -24.45
0.5Δ2 + Δ3 = -71.11
−
27.035
𝐸𝐼
Δ1 = 𝜃 𝑏 =
14.07
𝐸𝐼
Δ2 = 𝜃𝑐 =
−
78.145
𝐸𝐼
Δ3 = 𝜃 𝑑 =

18. • Step 8:
– Final Moments
𝑀 𝑎𝑏 = ̶ 80 kN-m
𝑀 𝑏𝑐 = 𝑀 𝐹
𝑏𝑐 +
2𝐸𝐼
𝐿 𝑏𝑐
2𝜃 𝑏 + 𝜃𝑐 −
3𝐸𝐼∆
𝐿 𝑏𝑐
= -60+
2𝐸(2𝐼)
8
(
2×(−27.035)
𝐸𝐼
+
(14.07)
𝐸𝐼
) = -80 kN-m
18

19. 𝑀𝑐𝑏 = 𝑀 𝐹
𝑐𝑏 +
2𝐸𝐼
𝐿 𝑏𝑐
2𝜃𝑐 + 𝜃 𝑏 −
3𝐸𝐼∆
𝐿 𝑏𝑐
= 60+
2𝐸(2𝐼)
8
(
2×(14.07)
𝐸𝐼
+
(−27.035
𝐸𝐼
) = 60.55kN-m
𝑀𝑐𝑑 = 𝑀 𝐹
𝑐𝑑 +
2𝐸𝐼
𝐿 𝑐𝑑
2𝜃𝑐 + 𝜃 𝑑 −
3𝐸𝐼∆
𝐿 𝑐𝑑
= -35.55+
2𝐸(1.5𝐼)
6
(
2×(14.07)
𝐸𝐼
+
(−78.145)
𝐸𝐼
) = -60.55 kN-m
𝑀 𝑑𝑐 = 𝑀 𝐹
𝑑𝑐 +
2𝐸𝐼
𝐿 𝑐𝑑
2𝜃 𝑑 + 𝜃𝑐 −
3𝐸𝐼∆
𝐿 𝑐𝑑
= 71.11+
2𝐸(1.5𝐼)
6
(
2×(−78.145)
𝐸𝐼
+
(14.07)
𝐸𝐼
) = 0
19

20. 20
40 kN 60 kN 80 kN
A B C
D
2m 4m 2m4m 4m
2 I 1.5 I
80 kN-m
60.55 kN-m
120 kN-m
106.66kN-m

21. • Assessment question:
• Analyze the continuous beam shown in figure using stiffness
matrix method.
21
70kN
A
B C
6m3m 5m
80kN/
m
100kN
2m
D
2 I 1.5 I I

22. THANK YOU
22