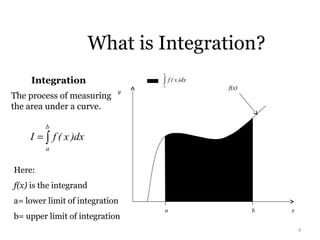
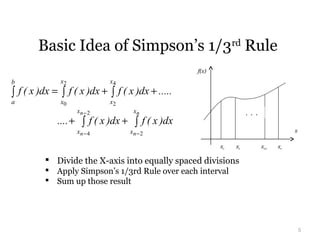
This document explains Simpson's 1/3rd rule for numerical integration. Simpson's 1/3rd rule approximates the integral of a function over an interval by breaking the interval into equal subintervals and approximating the function within each subinterval as a quadratic polynomial. The approximation takes the function values at the endpoints and midpoint of each subinterval. The approximations over all subintervals are then summed to give an approximation of the full integral. Important considerations for applying Simpson's 1/3rd rule include using an even number of equal subintervals and having a minimum of 3 points defined in each subinterval.

1. Hello!
1

2. Mehedi Hasan
2013-2-50-003
2

3. Simpson’s 1/3rd
Rule of
Integration

4. What is Integration?
∫=
b
a
dx)x(fI
Integration
4
The process of measuring
the area under a curve.
Here:
f(x) is the integrand
a= lower limit of integration
b= upper limit of integration
f(x)
a b
y
x
∫
b
a
dx)x(f

5. Basic Idea of Simpson’s 1/3rd
Rule
5
 Divide the X-axis into equally spaced divisions
 Apply Simpson’s 1/3rd Rule over each interval
 Sum up those result
f(x)
. . .
x0 x2 xn-2 xn
x
.....dx)x(fdx)x(fdx)x(f
x
x
x
x
b
a
++= ∫∫∫
4
2
2
0
∫∫
−
−
−
++
n
n
n
n
x
x
x
x
dx)x(fdx)x(f....
2
2
4

6. Basis of Simpson’s 1/3rd
Rule
Simpson’s 1/3rd rule is an extension of Trapezoidal rule
where the integrand is approximated by a second order
polynomial.
6
Hence
∫∫ ≈=
b
a
b
a
dx)x(fdx)x(fI 2
Where is a second order polynomial.)x(f2
2
2102 xaxaa)x(f ++=

7. Basis of Simpson’s 1/3rd
Rule
7
Choose
)),a(f,a( ,
ba
f,
ba











 ++
22
))b(f,b(and
as the three points of the function to evaluate a0, a1 and a2.
2
2102 aaaaa)a(f)a(f ++==
2
2102
2222





 +
+




 +
+=




 +
=




 + ba
a
ba
aa
ba
f
ba
f
2
2102 babaa)b(f)b(f ++==

8. Basis of Simpson’s 1/3rd
Rule
Solving the previous equations for a0, a1 and a2 give
22
22
0
2
2
4
baba
)a(fb)a(abf
ba
abf)b(abf)b(fa
a
+−
++




 +
−+
=
221
2
2
433
2
4
baba
)b(bf
ba
bf)a(bf)b(af
ba
af)a(af
a
+−
+




 +
−++




 +
−
−=
222
2
2
22
baba
)b(f
ba
f)a(f
a
+−






+




 +
−
=

9. Basis of Simpson’s 1/3rd
Rule
9
Then
∫≈
b
a
dx)x(fI 2
( )∫ ++=
b
a
dxxaxaa 2
210
b
a
x
a
x
axa 





++=
32
3
2
2
10
32
33
2
22
10
ab
a
ab
a)ab(a
−
+
−
+−=

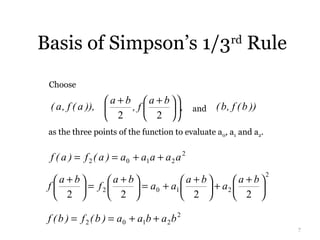
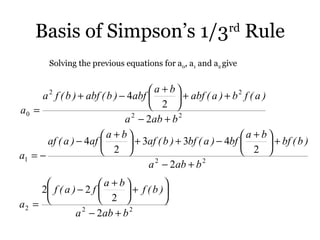
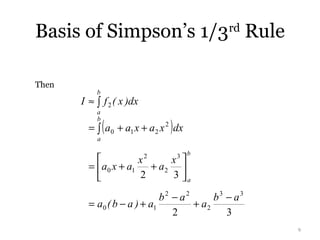
10. Basis of Simpson’s 1/3rd
Rule
10
Substituting values of a0, a1, a2 give




+




 +
+
−
=∫ )b(f
ba
f)a(f
ab
dx)x(f
b
a 2
4
6
2
Since for Simpson’s 1/3rd Rule, the interval [a, b] is broken
into 2 segments, the segment width
2
ab
h
−
=
it is called Simpson’s 1/3rd Rule.

11. 11
Important points to be considered while applying
Simpson’s 1/3 Rule are:
 Number of intervals must be an even
number.
 Minimum of 3 points are required
 Intervals are expected to be equal

12. THE END
• http://numericalmethods.eng.usf.edu
• http://esurveying.net/land-survey/earthwork-area-calculation-simpsons-13rd-rule
• http://mathworld.wolfram.com/SimpsonsRule.html