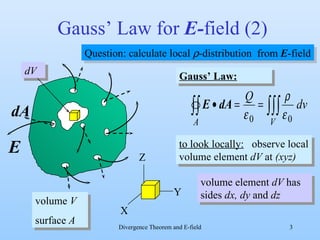
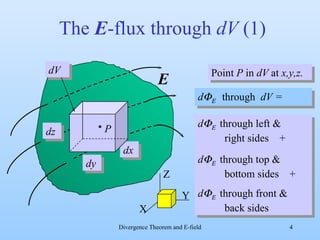
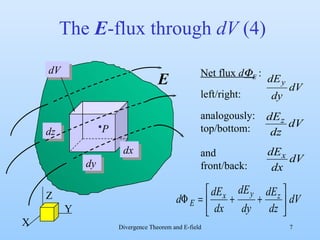
1) Gauss's law relates the electric flux through a closed surface to the enclosed electric charge. It can be used to calculate the electric field from a charge distribution if symmetry is present. 2) The document explores if there is an inverse expression that can locally calculate the charge density from the electric field. It examines calculating the electric flux through an infinitesimally small volume element. 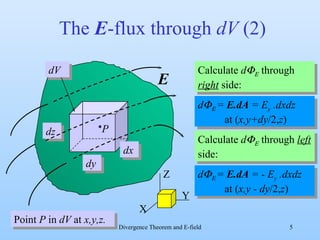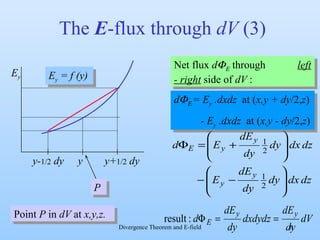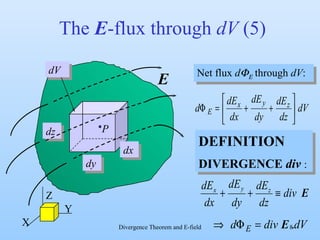3) By taking the sum of the fluxes through all sides of the small volume element and equating it to the enclosed charge, it derives that the divergence of the electric field equals the charge density divided by the permittivity of free space. This allows locally calculating the charge density from the electric field.

1. The Divergence Theorem and Electrical Fields © Frits F.M. de Mul

2. Gauss’ Law for E- field (1) Goal of this integral expression : to calculate E from  Q or   provided symmetry present !!!!! QUESTION: does an inverse expression, to locally calculate  (xyz) from E (xyz), exist ?? volume V; surface A dA ┴ surface A dA dA Gauss’ Law: E E E -field arbitrary

3. Gauss’ Law for E- field (2) volume element dV has sides dx, dy and dz Question: calculate local  - distribution from E -field volume V surface A E dA Gauss’ Law: dV to look locally: observe local volume element dV at (xyz) X Y Z

4. The E -flux through dV (1) d   through dV = d   through left & right sides + d   through top & bottom sides + d   through front & back sides E Point P in dV at x,y,z. Y dy dz dx dV X Z P

5. The E -flux through dV (2) Calculate d   through right side: d   = E.dA = E y .dxdz at ( x,y+dy /2, z ) Calculate d   through left side: d   = E.dA = - E y .dxdz at ( x,y - dy /2, z ) dV X Y Z dy dz dx E P Point P in dV at x,y,z.

6. The E -flux through dV (3) Net flux d   through left - right side of dV : Point P in dV at x,y,z. P y y+ 1/2 dy y- 1/2 dy d   = E y .dxdz at ( x,y + dy /2, z ) - E y .dxdz at ( x,y - dy /2, z ) E y E y = f (y)

7. The E -flux through dV (4) Net flux d   : left/right: analogously: top/bottom: and front/back: dV X Z dy dz dx E P Y

8. The E -flux through dV (5) Net flux d   through dV : DEFINITION DIVERGENCE div : dV X Z dy dz dx E P Y

9. Local expression for Gauss’ Law enclosed charge in dV :   dV Gauss’ Law in local form: where E and  are f (x,y,z) volume V surface A E dA dV element dV :

10. From “local” to “integral” summation over all elements: volume V surface A E dA dV element dV : all “internal” d  E ’s cancel d  E ’s at surface A remain only !

11. How to use the laws ? Integral expression: from   to E, but in symmetrical situations only ! div E (x,y,z) =  (x,y,z) /   Differential (local) expression: from E (x,y,z) to  (x,y,z) . volume V surface A E dA

12. Physical meaning of div Divergence = local “micro”-flux per unit of volume [m 3 ] volume V surface A E dA

13. “ Gauss” in general in accordance with general relation for a vector X : the end volume V surface A E dA