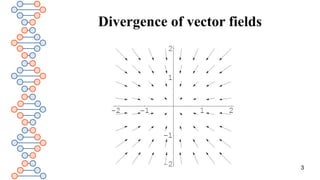
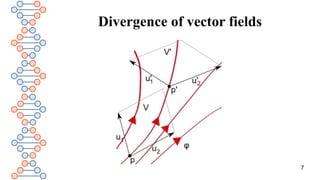
The document discusses the divergence of vector fields. It defines divergence as the infinitesimal relative change in volume when transporting a volume element along the flow of a vector field. It provides an abstract definition using Lie derivative and volume form. It then relates this to Maxwell's equations, stating that the divergence of the electric displacement field D equals the electric charge density, while the divergence of the magnetic flux density B is always zero since there are no magnetic monopoles.

1. Ms.S.Tamilselvan
Divergence of vector fields
Electromagnetic fields
1

2. Divergence of vector fields
The divergence of a vector field is the
infinitesimal relative change in volume when
transporting a volume element along its flow. The
abstract definition in terms of Lie derivative and
volume form is quite intuitive here.
2

3. Divergence of vector fields
3

4. Divergence of vector fields
Taking your (lack of) knowledge about differential geometry into account, this
might be too hard to follow, but here it goes anyway:
Let u1,…,un be some tangent vectors with base point p and ω the volume form,
ie V=ωp(u1,…,un) is the (possibly negative) volume of the parallelepiped
spanned by these vectors
In case of three dimensional Euclidean space, this is just the triple product
ωp(u1,u2,u3)=u1⋅(u2×u3)
4

5. Divergence of vector fields
Now, let X be a vector field (eg the electric or magnetic field) and φ its flow, ie p′
(ϵ)=φϵ(p) is the point you arrive at when moving along the field lines of X , starting at p
and with 'velocity' given by X and 'time' given by ϵ.
This maps the tangent vectors at p to u′k(ϵ)=Tφϵ(uk) at p′(ϵ).
Here, Tφϵ is the tangent map of φϵ (a kind of multi-dimensional derivative); in
coordinates, it is given by the Jacobian matrix.
5

6. Divergence of vector fields
The volume of the parallelepiped will change from V to
V′(ϵ)=ωp′(ϵ)(u′1(ϵ),…,u′n(ϵ))≡(φϵ∗ω)p(u1,…,un)
The divergence at p is the limit
(divX)(p)=limϵ→0(V′(ϵ)−V)/Vϵ
ie the infinitesimal relative change in volume when transporting a volume
element along the flow of a vector field.
6

7. Divergence of vector fields
7

8. Divergence of vector fields
The two maxwell equations using divergence are,
D⃗ =ρdivB⃗ =0
at least in differential form. In integral form they are maybe more clearer for
you. They are
∬∂VD⃗ dA⃗ =∭Vρ dV=Q(V)
∬∂VB⃗ dA⃗ =0
8

9. Divergence of vector fields
The first equation just means the electrical flux D through a close
surface of a volume V is proportionate to the electrical charge in this volume.
Or in much simpler word, divergence is a mathematical measure of the density
of your electrical flux so you can make conclusions of the number of electrical
charges.
To be a little more precise. The electrical field is something coming
out of sources (positive charges) and ends in sinks (negative charges). So if you
include just one source with your volume V
and a sink is somewhere out of your volume your divergence measures one
positive charge Q.
If your volume include two sources and a sink you will measure again just one
positive charge Q.
9

10. Divergence of vector fields
The second equation is the same but with magnetic flux. You will notice the
equation is always 0. This is because there are no sources or sinks in magnetic
charges, so the divergence of B⃗
must always be 0.
10

11. Divergence of vector fields
11