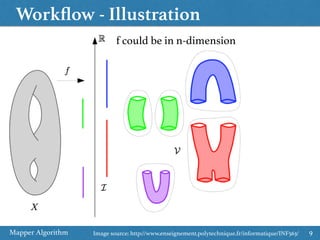
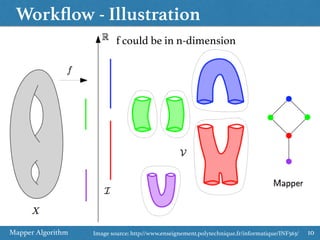
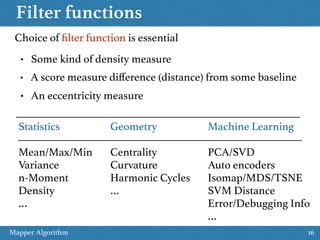
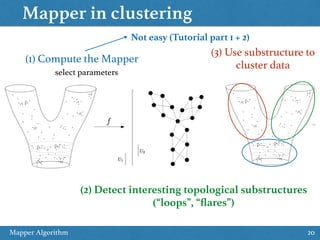
The document provides an overview of the Mapper algorithm, a technique from topological data analysis. It begins by introducing basic concepts from topology like Reeb graphs and Morse theory. It then describes the key steps of the Mapper algorithm: (1) defining a filter function on the data, (2) clustering inverse images of the filter, and (3) connecting clusters to form a graph. The document discusses practical considerations like choosing filter functions and parameters. It also provides examples of applying Mapper for tasks like clustering, feature selection, and data exploration.




![Morse theory
Mapper Algorithm 5
Basic idea
Describe topology of a smooth manifold M using level
sets of a suitable function h : M -> R
• Recover M by looking at h-1((∞, t]), as t scans over the
range of h
• Topology of M changes at critical points of h](https://image.slidesharecdn.com/01420160415tutorialoftopologicaldataanalysispartiiimapper-161011135158/85/Tutorial-of-topological-data-analysis-part-3-Mapper-algorithm-5-320.jpg)