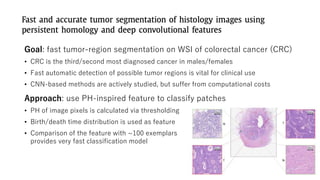
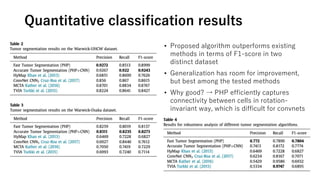
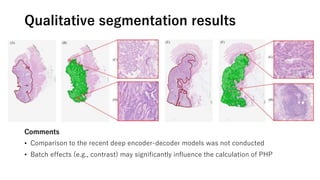
The document discusses the application of topological data analysis (TDA) in medical image analysis, specifically focusing on understanding transcriptomic characteristics in autism spectrum disorder (ASD) and colorectal cancer (CRC). It outlines the use of persistent homology to analyze high-dimensional gene expression data and proposes a CNN-based method for fast tumor-region segmentation in CRC using features derived from persistent homology. Results indicate that ASD patients exhibit more heterogeneous gene expression profiles compared to controls, and the proposed segmentation method shows improved classification performance over existing techniques.

1. Journal Club Sep. 18, 2020 (Ryohei Suzuki)
J. R. Soc. Interface 16.158 (2019): 16:20190531
Medical image analysis 55 (2019): 1-14.

2. Topological data analysis (TDA)
Why TDA?
• TDA provides metric-invariant
summarization of complex and
high-dimensional data
cf. many normalization modes of RNA-seq
• TDA robustly handles the global
structure of data in intuitive way
Applications of TDA
• Material science (crystal structure)
• Network analysis
• Peak detection, etc.
Topology（位相幾何学）
= mathematical framework for
describing the “shape” of object
that is invariant with respect to
continuous deformation

3. Basic framework of topological analysis
Figure copied from https://www.wpi-aimr.tohoku.ac.jp/hiraoka_labo/introduction_j.pdf ← recommended reference!
# Connected
Components
# Rings
(1d-cycle)
# Hollows
(2d-cycle)

4. Persistent homology
Assuming the input to be a point set, observe the transition of topological
features of the complex given by connecting points with growing radius ε
Lifetime of individual
connected components
Lifetime of individual rings
Robust ring
structure
Called “barcode”
Birth of ring Death of ring

5. Persistent diagram
Scatter graph showing the
birth-(x-axis) and death-time (y-axis)
of topological components
→ representing the information of
global structure of the data
Further analysis
- Calculating summarized values
e.g. sum of the cycle length SLk
- Classification of diagrams as images
Figure from https://www.pnas.org/content/113/26/7035
Robust ring
Transient
rings

6. Goal: discover the transcriptomic characteristics of ASD patients’ brains
• ASD is known to be highly heritable, but no key genetic variant contributing to the disease
is found. Rather, >100 genes are considered to contribute to the risk.
• Several studies have showed transcriptomic differences e.g., the downregulation of
neuronal synaptic genes and the upregulation of immune genes in ASD patients
• More comprehensive study is required to understand the disease
Approach: directly apply persistent homology to expression data
• To see the inter-patient and inter-gene geometries of ASD/healthy groups
Patient-space
Densely-packed topology
= patients have similar expression profiles
Sparsely-packed topology
= patients have heterogeneous expression

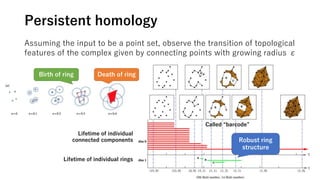
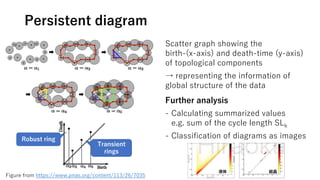
7. Dataset and study overview
Datasets
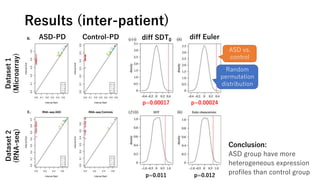
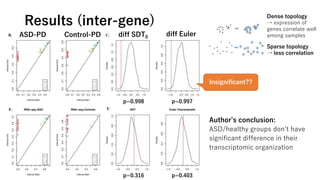
• Dataset 1: microarray (9934 genes, 29 ASD / 29 control) [1], log2-transformed
• Dataset 2: RNA-seq (22399 genes, 82 ASD / 82 control) [2], RPKM & log2-transformed
Procedure
• Calculate the inter-sample and inter-gene
distance matrices for ASD/control expression
• Dissimilarity measure: 1-r (r=Pearson correlation)
• Compute the persistent diagrams
• Derive the summary values
• SDT0
= sum of death times of connected components.
• Euler characteristics = SL0 – SL1 + SL2
※SLk is sum of lifespan of connected components (k=0), rings (k=1), hollows (k=2).
[1] Voineagu et al., (2011) Nature 474, 380-384 [2] Parikshak et al., (2016) Nature 540, 423-427
Sample 1 Sample 2 Sample 3
Gene 1 0.01 0.52 …
Gene 2 0.25
Gene 3 …
Inter-sample
Inter-gene

8. Results (inter-patient)
Dataset1
(Microarray)
Dataset2
(RNA-seq)
ASD-PD Control-PD diff SDT0 diff Euler
Random
permutation
distribution
ASD vs.
control
p=0.00017 p=0.00024
p=0.011 p=0.012
Conclusion:
ASD group have more
heterogeneous expression
profiles than control group

9. Results (inter-gene)
p=0.316 p=0.403
p=0.998 p=0.997
ASD-PD Control-PD diff SDT0 diff Euler
Author’s conclusion:
ASD/healthy groups don’t have
significant difference in their
transcriptomic organization
Insignificant??
Dense topology
→ expression of
genes correlate well
among samples
Sparse topology
→ less correlation

10. Goal: fast tumor-region segmentation on WSI of colorectal cancer (CRC)
• CRC is the third/second most diagnosed cancer in males/females
• Fast automatic detection of possible tumor regions is vital for clinical use
• CNN-based methods are actively studied, but suffer from computational costs
Approach: use PH-inspired feature to classify patches
• PH of image pixels is calculated via thresholding
• Birth/death time distribution is used as feature
• Comparison of the feature with ~100 exemplars
provides very fast classification model

11. Connecting pixels by thresholding
• Common way to calculate persistent homology for 2D image data
• By lowering the threshold, connected components advent and vanish
(merge) one after another.
Left image from: https://www.nature.com/articles/s41598-018-36798-y

12. Persistent homology profiles (PHP)
• From the thresholding result, probability distributions of birth/death-
time called PHP are constructed (green lines)
• These distributions are
treated as feature vectors
• By comparing PHP of
input data with those of
exemplar T/N images,
fast classification can be
performed.
birth death
tumor
mean
normal
mean
PHP

13. Exemplar selection using CNN activation
• Training dataset contains ~100000 patches
→ we should compare the PHP of input with some representative values
• Improper selection of exemplars
causes overfitting to significant
texture patterns
• Authors proposes a CNN-based
selection strategy where patches
with various feature activation
are equally respected Select k exemplars from
each bin of activation
strength
(highest 1/Q ~ lowest 1/Q)

14. Quantitative classification results
• Proposed algorithm outperforms existing
methods in terms of F1-score in two
distinct dataset
• Generalization has room for improvement,
but best among the tested methods
• Why good? → PHP efficiently captures
connectivity between cells in rotation-
invariant way, which is difficult for convnets

15. Qualitative segmentation results
Comments
• Comparison to the recent deep encoder-decoder models was not conducted
• Batch effects (e.g., contrast) may significantly influence the calculation of PHP

16. Reflection
• (+) Persistent homology provides unique information about the global
structure of the dataset, which is difficult to calculate in raw-data space,
which would be useful for very high-dimensional data with large noise
• (-) Persistent homology only provides highly summarized statistics,
discarding the information about contributions of individual data points,
e.g., which gene set is contributing in ASD patients.
• Combination with CNNs, which perform very good at discovering local
features, seems to be a promising idea for image analysis.