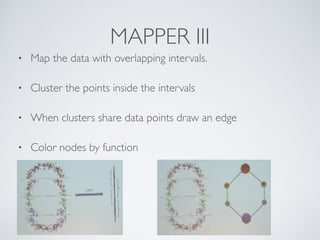
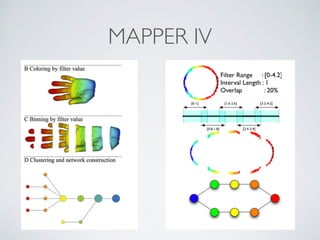
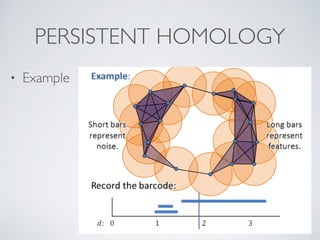
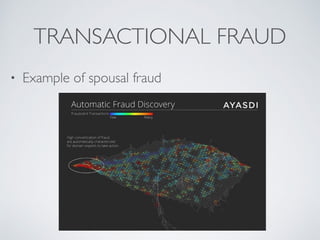
This document provides an overview of topological data analysis (TDA). It discusses how TDA marries 300-year old mathematics with modern data analysis to capture the shape of data. TDA techniques like Mapper are invariant to transformations of scale, position or pose, can compress large datasets while retaining important features, and function well with noisy or incomplete data. Mapper works by mapping data with overlapping intervals, clustering points within each interval, and connecting clusters that share data points to represent the topological structure. The document provides several examples of applying TDA and Mapper to problems in computer vision, healthcare, finance, and model interpretation.

1. TOPOLOGICAL DATA ANALYSIS
HJ vanVeen· Data Science· Nubank Brasil

2. TOPOLOGY I
• "When a truth is necessary, the reason for it can be
found by analysis, that is, by resolving it into simpler
ideas and truths until the primary ones are reached."
- Leibniz

3. TOPOLOGY II
• Topology is the mathematical study of topological
spaces.
• Topology is interested in shapes,
• More specifically: the concept of 'connectedness'

4. TOPOLOGY III
• A topologist is someone who does not see the
difference between a coffee mug and a donut.

5. HISTORY I
• “Nothing at all takes place in the universe in which
some rule of maximum or minimum does not
appear.” - Euler
• Seven Bridges of Koningsbrucke: devise a walk
through the city that would cross each bridge
once and only once.

6. HISTORY II

7. HISTORY III
• Euler's big insights:
• Doesn’t matter where you start walking, only matters which bridges
you cross.
• A similar solution should be found, regardless where you start your
walk.
• only the connectedness of bridges matter,
• a solution should also apply to all other bridges that are connected
in a similar fashion, no matter the distances between them.

8. HISTORY IV
• We now call these graph walks ‘Eulerian walks’ in
Euler’s honor.
• Euler's first proven graph theory theorem:
• 'Euler walks' are possible if exactly zero or two nodes
have an odd number of edges.

9. TDA I
• TDA marries 300-year old maths with
modern data analysis.
• Captures the shape of data
• Is invariant
• Compresses large datasets
• Functions well in the presence of noise / missing variables

10. TDA II
• Capturing the shape of data
•Traditional techniques like clustering or dimensionality reduction have
trouble capturing this shape.

11. TDA III
• Invariance.
• Euler showed that only connectedness matters.The size, position, or
pose of an object doesn't change that object.

12. TDA IV
• Compression.
• Compressed representations use
the order in data.
• Only order can be compressed.
• Random noise or slight variations
are ignored.
• Lossy compression retains the most
important features.
• "Now where there are no parts, there neither extension, nor shape, nor divisibility is possible.
And these monads are the true atoms of nature and, in a word, the elements of things." - Leibniz

13. MAPPER I
• Mapper was created by Ayasdi Co-founder
Gurjeet Singh during his PhD under Gunnar
Carlsson.
• Based on the idea of partial clustering of the data
guided by a set of functions defined on the data.

14. MAPPER II
• Mapper was inspired by the Reeb Graph.

15. MAPPER III
• Map the data with overlapping intervals.
• Cluster the points inside the intervals
• When clusters share data points draw an edge
• Color nodes by function

16. MAPPER IV

17. MAPPERV
Distance_to_median(row) x y z
1.5 1.5 1.5 1.5
1.5 -0.5 -0.5 -0.5
0 1 1 1
0 1 0.9 1.1
3 2 2 2
3 2.1 1.9 2
Y

18. MAPPERVI
• In conclusion:

19. FUNCTIONS
• Raw features or point-cloud axis / coordinates
• Statistics: Mean, Max, Skewness, etc.
• Mathematics: L2-norm, FourierTransform, etc.
• Machine Learning: t-SNE, PCA, out-of-fold preds
• Deep Learning: Layer activations, embeddings

20. CLUSTER ALGO’S
• DBSCAN / HDBSCAN:
• Handles noise well.
• No need to set number of clusters.
• K-Means:
• Creates visually nice simplicial complexes/graphs

21. SOME GENERAL USE CASES
• ComputerVision
• Model and feature inspection
• Computational Biology / Healthcare
• Persistent Homology

22. COMPUTERVISION
• Demo

23. MODEL AND FEATURE
INSPECTION
• Demo

24. COMPUTATIONAL BIOLOGY
• Example

25. PERSISTENT HOMOLOGY
• Example

26. SOME FINANCE USE CASES
• Customer Segmentation
• Transactional Fraud
• Accurate Interpretable Models
• Exploration / Analysis

27. CUSTOMER SEGMENTATION
• Demo

28. TRANSACTIONAL FRAUD
• Example of spousal fraud

29. ACCURATE INTERPRETABLE
MODELS
• Create: global linear model
• Function: L2-norm
• Color: Heatmap by ground truth and animate to out-of-fold model predictions
• Identify: Low accuracy sub graphs
• Select: Features that are most important for sub graphs
• Create: Local linear models on sub graphs
• Stack: DecisionTree
• Compare: Divide-and-Conquer and LIME
• DEMO

30. EXPLORATION / ANALYSIS
• Demo

31. QUESTIONS?

32. FURTHER READING
• Google terms:
• Ayasdi,Topological Data Analysis, Robert Ghrist, Gurjeet Singh, Gunnar Carlsson,
Anthony Bak,Allison Gilmore, Simplicial Complex, Python Mapper.
• Videos:
• https://www.youtube.com/watch?v=4RNpuZydlKY
• https://www.youtube.com/watch?v=x3Hl85OBuc0
• https://www.youtube.com/watch?v=cJ8W0ASsnp0
• https://www.youtube.com/watch?v=kctyag2Xi8o