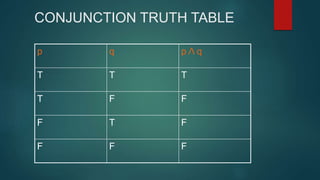
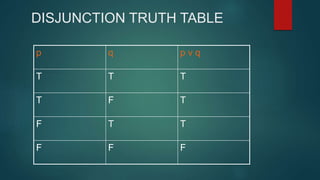
The document discusses truth tables and their use in determining the validity of arguments. It defines truth tables as listings of all possible combinations of true and false statements and the resulting truth values. It then explains conjunction, disjunction, negation, and logical equivalence through truth tables. Conjunction uses AND and is true only when both statements are true. Disjunction uses OR and is true if either statement is true. Negation reverses the truth value of a statement. Logical equivalence means statements have identical truth tables.

1. Topic: Truth table
Discrete Mathematics
Department of CSE

2. Introduction
 The truth value of a statement is the classification as
true or false which denoted by T or F.
 A truth table is a listing of all possible combinations of
the individual statements as true or false, along with
the resulting truth value of the compound statements.
 Truth tables are an aide in distinguishing valid and
invalid arguments.

3.  Conjunction
 Disjunction
 Negation
 Logical equivalence

4. Conjunction
 Joining two statements with AND forms a
compound statement called a conjunction.
 p Λ q Read as “p and q”
 The truth value is determined by the possible
values of ITS sub statements.
 To determine the truth value of a compound
statement we create a truth table

5. CONJUNCTION TRUTH TABLE
p q p Λ q
T T T
T F F
F T F
F F F

6. Disjunction
 Joining two statements with OR forms a compound statement
called a “disjunction.
 p ν q Read as “p or q”
 The truth value is determined by the possible values of ITS sub
statements.
 To determine the truth value of a compound statement we
create a truth table

7. DISJUNCTION TRUTH TABLE
p q p ν q
T T T
T F T
F T T
F F F

8. NEGATION
 ¬Type equation here. p read as not p
 Negation reverses the truth value of any statement

9. NEGATION TRUTH TABLE
P ¬P
T F
F T

10. Truth Table for ¬p
 Recall that the negation of a
statement is the denial of the
statement.
 If the statement p is true, the
negation of p, i.e. ~p is false.
 If the statement p is false, then ¬p
is true.
 Note that since the statement p
could be true or false, we have 2
rows in the truth table.
p ¬p
T F
F T

11. LOGICAL EQUIVALENCE
 Two propositions P(p , q,…) and Q(p , q, …) are said to
be logically equivalent, or simply equivalent or equal
when they have identical truth tables.
 ¬(p Λ q) ≡ ¬p V ¬q

12. Logical Equivalence
p q p^q ¬(p^q)
T T T F
T F F T
F T F T
F F F T
p q ¬p ¬q ¬pV¬q
T T F F F
T F F T T
F T T F T
F F T T T

13. Truth Table for p ^ q
 Recall that the conjunction is the
joining of two statements with the
word and.
 The number of rows in this truth
table will be 4. (Since p has 2 values,
and q has 2 value.)
 For p ^ q to be true, then both
statements p, q, must be true.
 If either statement or if both
statements are false, then the
conjunction is false.
p q p ^ q
T T T
T F F
F T F
F F F

14. Truth Table for p v q
 Recall that a disjunction is the joining
of two statements with the word or.
 The number of rows in this table will
be 4, since we have two statements
and they can take on the two values
of true and false.
 For a disjunction to be true, at least
one of the statements must be true.
 A disjunction is only false, if both
statements are false.
p q p v q
T T T
T F T
F T T
F F F

15. Truth Table for p  q
 Recall that conditional is a compound
statement of the form “if p then q”.
 Think of a conditional as a promise.
 If I don’t keep my promise, in other
words q is false, then the conditional
is false if the premise is true.
 If I keep my promise, that is q is true,
and the premise is true, then the
conditional is true.
 When the premise is false (i.e. p is
false), then there was no promise.
Hence by default the conditional is
true.
p q p  q
T T T
T F F
F T T
F F T

16. Equivalent Expressions
 Equivalent expressions are
symbolic expressions that
have identical truth values for
each corresponding entry in a
truth table.
 Hence ¬ (¬p) ≡ p.
 The symbol ≡ means
equivalent to.
p ¬p ¬(¬p)
T F T
F T F

17. De Morgan’s Laws
 The negation of the conjunction p ^ q is given by ~(p ^ q) ≡ ~p v ~q.
“Not p and q” is equivalent to “not p or not q.”
 The negation of the disjunction p v q is given by ~(p v q) ≡ ~p ^ ~q.
“Not p or q” is equivalent to “not p and not q.”