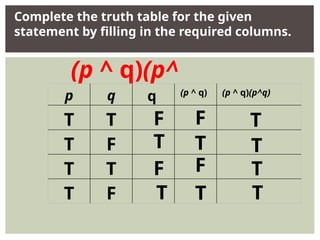
The document discusses the truth values of compound propositions and the definitions of various logical operators such as negation, conjunction, disjunction, conditional, and biconditional. It explains how truth tables are constructed to determine the truth or falsity of these propositions based on their components. Additionally, the document emphasizes specific conditions under which these logical statements are true or false.

1. TRUTH VALUES
OF COMPOUND
PROPOSITION

2. LOGICAL
OPERATORS
LOGICAL
CONNECTORS
SYMBOL
NEGATION
CONJUNCTION
DISJUNCTION
CONDITIONAL
BICONDITION
AL
NO
T
^
“AND” (but, yet,
moreover, still, also,
furthermore,
although)
O
R
V
→
↔
If-
then
If and only
if

3. CONSTRUCTI
NG TRUTH
TABLES

4. The truth value of a proposition is either
true or false but not both.
The truth or falsity of compound
proposition is completely determined by
the truth or falsity of its components.
Truth Value of the Propositions

5. TRUTH TABLES
A truth table involving propositions
has rows.
22
=4 𝑟𝑜𝑤𝑠
23
=8 𝑟𝑜𝑤𝑠

6. LOGICAL
OPERATORS/CONNECTORS
𝑁 𝑒𝑔𝑎𝑡𝑖𝑜𝑛
𝐶𝑜𝑛𝑗𝑢𝑛𝑐𝑡𝑖𝑜𝑛
𝐷𝑖𝑠𝑗𝑢𝑛𝑐𝑡𝑖𝑜𝑛
𝐶 𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛𝑎𝑙
𝐵𝑖𝑐𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛𝑎𝑙
not
and
Either, or
If-then
If and only

7. The negation of a proposition is
denoted by (not p) and is defined
through its truth table
NEGATION
T F
F T

8. Fill in the truth values.
TRY THIS!
F
T
T
T

9. The conjunction of a proposition and q is
denoted by : (p and q) and is defined
through its truth table
CONJUNCTIO
N
Note : The conjunction p^q
is TRUE only when both
conjucts p and q are true
as shown in its truth table;
otherwise the conjunction
is FALSE.
p q p^q
T T T
T F F
F T F
F F F

10. Fill in the truth values.
TRY THIS!
T T
T F
F T
F F
F T
T T
T F
T T

11. The disjunction of a proposition and q is
denoted by p V q: (p or q) and is defined
through its truth table
DISJUNCTION
Note : The disjunction p V q
is TRUE when one of the
statement is true. The
disjunction p V q is FALSE
when both p and q are
false.
p q p V q
T T T
T F T
F T T
F F F

12. Fill in the truth values.
TRY THIS!
T T
T F
F T
F F
F T
T T
F T
F T

13. The conditional of a proposition and q is
denoted by p q: (If p, then q) and is defined
through its truth table
CONDITIONA
L
Note : The proposition p is called
the hypothesis, while the
proposition q is called the
conclusion. A conditional
statement may be considered
FALSE if a TRUE hypothesis is
followed by a FALSE conclusion.
p q p q
T T T
T F F
F T T
F F T

14. Fill in the truth values.
TRY THIS!
T F
F T
T F
F F

15. The conditional of a proposition and q is
denoted by p q: (p if and only if q) and is
defined through its truth table
BICONDITIONA
L
Note : If both p and q are
either TRUE or FALSE, then
the biconditional is TRUE;
otherwise it is FALSE.
p q p q
T T T
T F F
F T F
F F T

16. Fill in the truth values.
TRY THIS!
T T
F T
T F
F F

17. LOGICAL
OPERATOR
S
CONNECTO
R
SYMBOL
When is it
TRUE?
When is it
FALSE?
NEGATION
CONJUNCTIO
N
DISJUNCTIO
N
CONDITIONA
L
BICONDITIO
NO
T
^
“AND” (but, yet,
moreover, still,
also,
furthermore,
although)
The conjunction
p^q is TRUE only
when both
conjucts p and q
are true.
The disjunction
p V q is FALSE
when both p
and q are false.
O
R
V
When one
conjunct is
false.
The disjunction p V
q is TRUE when at
least one
statement is true.
→
↔
If-
then
If and
only if
A conditional
statement may be
considered FALSE if
a TRUE hypothesis
is followed by a
FALSE conclusion
If both p and q are
either TRUE or
FALSE, then the
biconditional is
TRUE

18. p (p V q)
p q
T T
T F
F T
F F
(p V
q)
p (p V q)
T
T
T
F
T
T
T
T

19. (p q)^((
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F
𝒑 (p q)
F
(p r) (p q)^((
F
F
F
T
T
T
T
T
T
F
F
T
T
T
T
T
T
T
T
T
F
T
F
T
T
F
F
T
F
T
F

20. (p q)V((
p q r
T T T
T T F
T F T
T F F
F T T
F T F
F F T
F F F
𝒑 (p q)
F
(p r) (p q)V((
F
F
F
T
T
T
T
T
T
F
F
T
T
T
T
T
T
T
T
F
T
F
T
T
T
T
T
T
T
T
T
TRY
THIS!!!
𝒓
F
T
F
T
F
T
F
T

21. (p ^ q)(p^
p q
T T
T F
T T
T F
(p ^ q) (p ^ q)(p^q)
F
T
F
T
F
T
F
T
q
T
T
T
T
Complete the truth table for the given
statement by filling in the required columns.