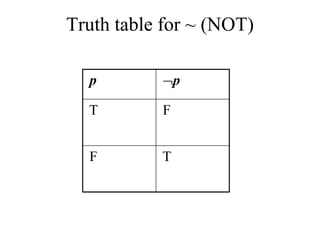
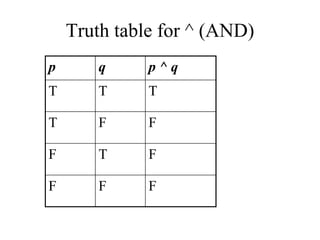
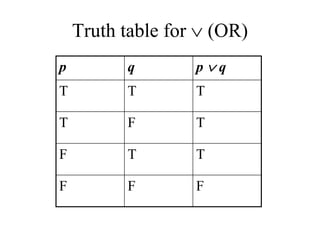
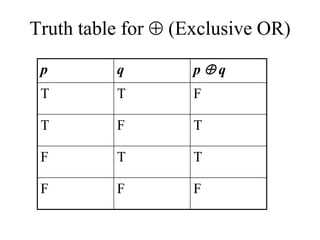
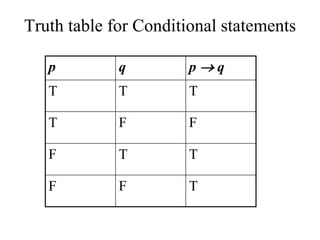
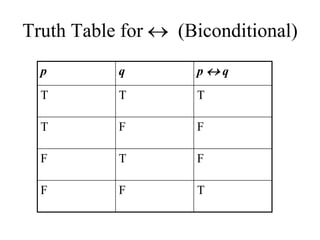
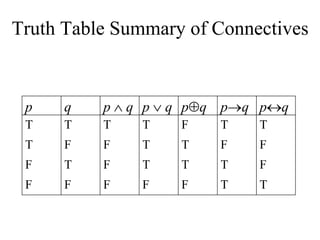
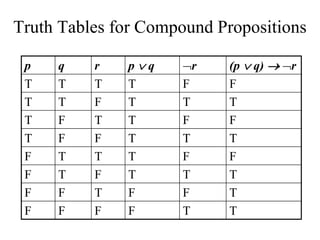
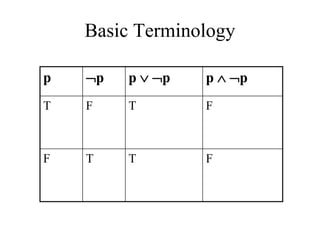
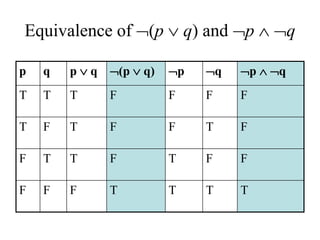
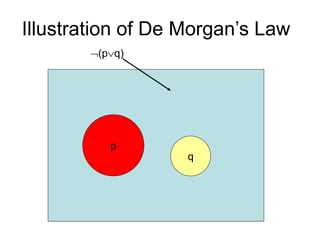
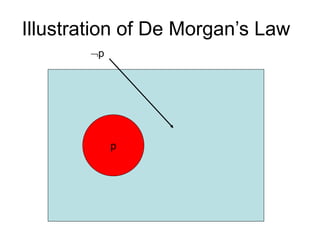
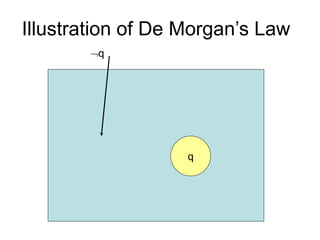
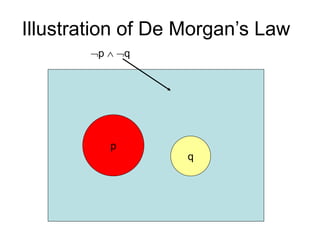
- The document summarizes key concepts in propositional logic, including simple and compound propositions, logical operators like negation, conjunction, disjunction, implication, equivalence, and truth tables. - It introduces important logical equivalences like De Morgan's laws, distribution, absorption, double negation, and equivalences involving implications. These equivalences allow proving that two propositions are logically equivalent without constructing a full truth table.

1. CS202
Discrete Maths
Chapter 1, Section 1.1
Propositional Logic
These class notes are based on material from our
textbook, Discrete Mathematics and Its
Applications, 6th ed., by Kenneth H. Rosen. They
are intended for classroom use only and are not a
substitute for reading the textbook.

2. Proposition
• Statement that is true or false.
• Examples:
– The capital of New York is Albany.
– The moon is made of green cheese.
– Go to town. (not a proposition – why?)
– What time is it? (not a proposition – why?)
– x + 1 = 2 (not a proposition – why?)

3. Simple/Compound Propositions
• A simple proposition has a value of T/F
• A compound proposition is constructed from
one or more simple propositions using logical
operators
• The truth value of a compound proposition
depends on the truth values of the constituent
propositions

4. Negation (NOT)
• NOT can be represented by the ~ or 
symbols
• NOT is a logical operator:
p: I am going to town.
 p: I am not going to town.

5. Truth table for ~ (NOT)
p p
T F
F T

6. Truth Tables
• A truth table lists ALL possible values of a
(compound) proposition
– one column for each propositional variable
– one column for the compound proposition
– 2n rows for n propositional variables

7. Conjunction (AND)
• The conjunction AND is a logical operator
p: I am going to town.
q: It is raining.
p  q: I am going to town and it is raining.
• Both p and q must be true for the conjunction
to be true.

8. Truth table for ^ (AND)
p q p ^ q
T T T
T F F
F T F
F F F

9. Disjunction (OR)
• Inclusive or - only one proposition needs to be
true for the disjunction to be true.
p: I am going to town.
q: It is raining.
p  q: I am going to town or it is raining.

10. Truth table for  (OR)
p q p  q
T T T
T F T
F T T
F F F

11. Exclusive OR
• Only one of p and q are true (not both).
p: I am going to town.
q: It is raining.
p  q: Either I am going to town or it is raining.

12. Truth table for  (Exclusive OR)
p q p  q
T T F
T F T
F T T
F F F

13. Conditional statements
• A conditional statement is also called an
implication or an if .. then statement.
• It has the form p  q
p: I am going to town.
q: It is raining.
p  q: If I am going to town, then it is raining.
• The implication is false only when p is true and
q is false!

14. Truth table for Conditional statements
p q p  q
T T T
T F F
F T T
F F T

15. Implication - Equivalent Forms
• If p, then q
• p implies q
• If p, q
• q if p
• q whenever p
• p is a sufficient condition for q
• q is a necessary condition for p
• p only if q

16. Converse of an Implication
• Implication: p  q
• Converse: q  p
• Implication:
– If I am going to town, it is raining.
• Converse:
– If it is raining, then I am going to town.

17. Converse of an Implication
p q q  p
T T T
T F T
F T F
F F T
(for p  q, this would be F)
(for p  q, this would be true)

18. Contrapositive of an Implication
• Implication: p  q
• Contrapositive: q  p
• Implication:
– If I am going to town, it is raining.
• Contrapositive:
– If it is not raining, then I am not going to town.
• The contrapositive has the same truth table as
the original implication.

19. Inverse of an Implication
• Implication: p  q
• Inverse: p  q
• Implication:
– If I am going to town, it is raining.
• Inverse:
– If I am not going to town, then it is not raining.
• The inverse of an implication has the same
truth table as the converse of that implication.

20. Biconditional
• “if and only if”, “iff”
• p  q
• I am going to town if and only if it is raining.
• Both p and q must have the same truth value
for the assertion to be true.

21. Truth Table for  (Biconditional)
p q p  q
T T T
T F F
F T F
F F T

22. Truth Table Summary of Connectives
F
F
T
T
p
F
T
F
T
q pq
pq
pq
p  q
p  q
T
T
F
F
F
F
T
T
T
F
F
F
T
T
F
T
T
F
T
T

23. Practice
• You do not learn the
simple things well.
• If you learn the simple
things well then the
difficult things become
easy.
• If you do not learn the
simple things well, then
the difficult things will not
become easy.
• The difficult things
become easy but you did
not learn the simple things
well.
• You learn the simple
things well but the
difficult things did not
become easy.
p: You learn the simple things well.
q: The difficult things become easy.

24. Practice
• You do not learn the
simple things well.
• If you learn the simple
things well then the
difficult things become
easy.
• If you do not learn the
simple things well, then
the difficult things will not
become easy.
• The difficult things
become easy but you did
not learn the simple things
well.
• You learn the simple
things well but the
difficult things did not
become easy.
p: You learn the simple things well.
q: The difficult things become easy.
p
pq
p  q
q  p
p  q

25. Compound Propositions
• To construct complex truth tables, add
intermediate columns for smaller (compound)
propositions
• One column for each propositional variable
• One column for each compound proposition
• For n propositional variables there will be 2n
rows
• Example:
(p  q)  r

26. Truth Tables for Compound Propositions
p q r p  q r (p  q)  r
T T T T F F
T T F T T T
T F T T F F
T F F T T T
F T T T F F
F T F T T T
F F T F F T
F F F F T T

27. Precedence of Logical Operators
• Parentheses gets the highest precedence
• Then:
Operator Precedence
 1
 2
 3
 4
 5

28. Precedence of Logical Operators
• Examples:
p  q  r means (p  q)  r, not p  (q  r)
p  q  r means (p  q)  r

29. Translating English Sentences
• To remove natural language ambiguity
• Helps in reasoning
• Examples:
– You can access the Internet from campus
only if you are a computer science major or
you are not a freshman.
– You cannot ride the roller coaster if you are
under 4 feet tall unless you are older than 16
years old.

30. Logic and Bit Operations
• Binary numbers use bits, or binary digits.
• Each bit can have one of two values:
1 (which represents TRUE)
0 (which represents FALSE)
• A variable whose value can be true or false is
called a Boolean variable. A Boolean variable’s
value can be represented using a single bit.

31. Logic and Bit Operations
• Computer bit operations are exactly the same as the logic
operations we have just studied. Here is the truth table
for the bit operations OR, AND, and XOR:
x y x  y x  y x  y
0 0 0 0 0
0 1 1 0 1
1 0 1 0 1
1 1 1 1 0

32. CS202
Discrete Maths
Chapter 1, Section 1.2
Propositional Equivalences

33. Basic Terminology
• A tautology is a proposition which is always
true. Example:
p  p
• A contradiction is a proposition that is always
false. Example:
p  p

34. Basic Terminology
p p p  p p  p
T F T F
F T T F

35. Basic Terminology
• A contingency is a proposition that is neither a
tautology nor a contradiction. Example:
p  q  r

36. Logical Equivalences
• Two propositions p and q are logically
equivalent if they have the same truth values in
all possible cases.
• Two propositions p and q are logically
equivalent if p  q is a tautology.
• Notation: p  q or p  q

37. Determining Logical Equivalence
• Consider the following two propositions:
(p  q)
p  q
• Are they equivalent? Yes. (They are part of
DeMorgan’s Law, which we will see later.)
• To show that (p  q) and p  q are
logically equivalent, you can use a truth table:

38. Equivalence of (p  q) and p  q
p q p  q (p  q) p q p  q
T T T F F F F
T F T F F T F
F T T F T F F
F F F T T T T

39. q
p
(pq)
Illustration of De Morgan’s Law

40. p
p
Illustration of De Morgan’s Law

41. q
q
Illustration of De Morgan’s Law

42. q
p
p  q
Illustration of De Morgan’s Law

43. Show that: p  q  p  q
p q p p  q p  q
T T F T T
T F F F F
F T T T T
F F T T T

44. Example: Distribution
Prove that: p  (q  r)  (p  q)  (p  r)
p q r qr p(qr) pq pr (pq)(pr)
T T T T T T T T
T T F F T T T T
T F T F T T T T
T F F F T T T T
F T T T T T T T
F T F F F T F F
F F T F F F T F
F F F F F F F F
44

45. Prove: pq(pq)  (qp)
p q pq pq qp (pq)(qp)
T T T T T T
T F F F T F
F T F T F F
F F T T T T
We call this biconditional equivalence.
45

46. Determining Logical Equivalence
• This is not a very efficient method. Why?
• To be more efficient, we develop a series of
equivalences, and use them to prove other
equivalences.

47. Important Equivalences
Identity
p  T  p
p  F  p
Double Negation
( p)  p
Domination
p  T  T
p  F  F
Idempotent
p  p  p
p  p  p

48. Important Equivalences
Commutative
p  q  q  p
p  q  q  p
Associative
(p  q)  r  p  (q  r)
(p  q)  r  p  (q  r)
Distributive
p  (q  r)  (p  q)  (p  r)
p  (q  r)  (p  q)  (p  r)
De Morgan’s
(p  q)  p  q
(p  q)  p  q

49. Important Equivalences
Absorption
p  (p  q)  p
p  (p  q)  p
Negation
p  p  T
p  p  F
Miscellaneous
p  p  T Or Tautology
p  p  F And Contradiction
(pq)  (p  q) Implication Equivalence
pq(pq)  (qp) Biconditional Equivalence

50. Example
Show that (p  q) and p  q are logically
equivalent:
(p  q)  (p  q) Example 3
 (p)  q 2nd DeMorgan law
 p  q double negation law
Q.E.D

51. Example
Show that (p  (p  q)) and p  q are
logically equivalent:
(p  (p  q))  p  (p  q) 2nd DeMorgan
 p  [(p)  q) 1st DeMorgan
 p  (p  q) double negation
 (p  p)  ( p  q) 2nd distributive
 FALSE  ( p  q) negation
 ( p  q)  FALSE commutative
 p  q identity
Q.E.D

52. Equivalences Involving Implications
p → q  p  q
p → q  q → p
p  q  p → q
p  q  (p → q)
(p → q)  p  q
(p → q)  (p → r)  p → (q  r)
(p → r)  (q → r)  (p  q) → r
(p → q)  (p → r)  p → (q  r)
(p → r)  (q → r)  (p  q) → r

53. Equivalences Involving Biconditionals
p ↔ q  (p → q)  (q → p)
p ↔ q  p ↔ q
p ↔ q  (p  q)  (p  q)
(p ↔ q )  p ↔ q

54. Example
• Show that (p  q)  (p  q) is a tautology.
(p  q)  (p  q)  (p  q)  (p  q) Example 3
 (p  q)  (p  q) 1st DeMorgan law
 p  (q  (p  q)) Associative law
 p  ((p  q)  q) Commutative law
 (p  p)  (q  q) Associative law
 TRUE  TRUE Example 1
 TRUE Domination law
QED

55. CS202
Discrete Maths
Chapter 1, Section 1.3
Predicates and Quantifiers

56. Predicates
• A predicate is a statement that contains variables.
• Ex: Let P(x) denote x > 3
• P(x) has no truth value until the variable x is bound by either
– assigning it a value or by
– quantifying it.
• Examples:
P(x) : x > 3
Q(x,y) : x = y + 3
R(x,y,z) : x + y = z
• The area of logic that deals with predicates and quantifiers is called predicate
calculus

57. Assignment of values
Let Q(x,y) denote “x + y = 7”.
Each of the following can be determined as T or F.
Q(4,3)
Q(3,2)
Q(4,3)  Q(3,2)
[Q(4,3)  Q(3,2)]

58. Predicates
• A predicate becomes a proposition if the
variables contained in it are either:
– Assigned specific values
– Quantified (all, many, some, few, none)
P(x) : x > 3
What are the truth values of P(4) and P(2)?
Q(x,y) : x = y + 3
What are the truth values of Q(1, 2) and Q(3, 0)?

59. Quantifiers
• Two types of quantifiers
– Universal quantifier: 
– Existential quantifier: 
• Universe of discourse - the particular
domain of the variable in a propositional
function

60. Universal Quantification
• P(x) is true for all values of x in the universe of
discourse.
x P(x) – When TRUE? When FALSE?
“for all x, P(x)”
“for every x, P(x)”
• The variable x is bound by the universal
quantifier, producing a proposition.

61. Examples
• U = {all real numbers}, P(x): x+1 > x
– What is the truth value of x P(x)
• U = {all real numbers}, Q(x): x < 2
– What is the truth value of x Q(x)
• U = {all students in CS202}
R(x) : x has an account on CSLab
– What does x R(x) mean?

62. For universal quantification
P(x)  P(x1)  P(x2)  …  P(xn)
• If the elements in the universe of discourse can be listed,
then U = {x1, x2, …, xn}
x P(x)  P(x1)  P(x2)  …  P(xn)
• Example
U = {positive integers not exceeding 3} and P(x): x2 < 10
– What is the truth value of x P(x)?
P(1)  P(2)  P (3)
T  T  T
T

63. Existential Quantification
• P(x) is true for some x in the universe of
discourse
x P(x) - When TRUE? When FALSE?
“for some x, P(x)”
“There exists an x such that P(x)”
“There is at least one x such that P(x)”
• The variable x is bound by the existential
quantifier, producing a proposition

64. Example
• U = {all real numbers}, P(x): x > 3
– What is the truth value of  x P(x)
• U = {all real numbers}, Q(x): x = x + 1
– What is the truth value of  x Q(x)
• U = {all students in CS202},
R(x) : x has an account on CSlab
– What does  x R(x) mean?

65. For existential quantification
P(x)  P(x1)  P(x2)  …  P(xn)
• If the elements in the universe of discourse can be listed,
U = {x1, x2, …, xn}
x P(x)  P(x1)  P(x2)  …  P(xn)
• Example
U = {positive integers not exceeding 4} and P(x): x2 > 10
– What is the truth value of x P(x)?
P(1)  P(2)  P(3)  P(4)
T  T  T  F
T

66. Quantifiers
xP(x)
•True when P(x) is true for every x.
•False if there is an x for which P(x) is false.
xP(x)
•True if there exists an x for which P(x) is true.
•False if P(x) is false for every x.

67. Binding Variables
• Bound variable: if a variable is quantified
• Free variable: Neither bound nor assigned a
specific value
– Example: x P(x) x Q(x,y)
• Scope of Quantifiers: Part of a logical
expression to which a quantifier is applied
– Example: x (P(x)  Q(x))  x R(x)

68. Negation of Quantifiers
• Distributing a negation operator across a
quantifier changes a universal to an existential
and vice versa.
~x P(x)  x ~P(x)
~x P(x)  x ~P(x)

69. Negation (it is not the case)
xP(x) equivalent to xP(x)
•True when P(x) is false for every x
•False if there is an x for which P(x) is true.
 xP(x) is equivalent to xP(x)
•True if there exists an x for which P(x) is false.
•False if P(x) is true for every x.

70. Examples 2a
Let T(a,b) denote the propositional function “a
trusts b.” Let U be the set of all people in the
world.
Everybody trusts Bob.
xT(x,Bob)
Could also say: xU T(x,Bob)
 denotes membership
Bob trusts somebody.
xT(Bob,x)

71. Examples 2b
Alice trusts herself.
T(Alice, Alice)
Alice trusts nobody.
x T(Alice,x)
Carol trusts everyone trusted by David.
x(T(David,x)  T(Carol,x))
Everyone trusts somebody.
x y T(x,y)

72. Examples 2c
x y T(x,y)
Someone trusts everybody.
y x T(x,y)
Somebody is trusted by everybody.
Bob trusts only Alice.
x (x=Alice  T(Bob,x))

73. Bob trusts only Alice.
x (x=Alice  T(Bob,x))
Let p be “x=Alice”
q be “Bob trusts x”
p q p  q
T T T
T F F
F T F
F F T
True only when Bob trusts
Alice or Bob does not trust
someone who is not Alice

74. Negation of Quantifiers
• Example:
Assume the domain of x is: {students in CS202}, and
P(x) : x has taken a course in calculus.
Then x P(x)
means “All students in CS202 have taken a course in
calculus.”
The negation of this statement would be, “Not every
student in CS202 has taken a course in calculus,” or
“There exists some student in CS202 who has not taken
a course in calculus.” This would be:
x P(x)

75. Translating from English
• There are many ways to translate a given
sentence
• The goal is to produce a logical expression that is
simple and can be easily used in subsequent
reasoning
• Steps:
– Clearly identify the appropriate quantifier(s)
– Introduce variable(s) and predicate(s)
– Translate using quantifiers, predicates, and logical
operators

76. Example
“Every student in this class has studied calculus.”
• Solution 1
– Assume, U = {all students in CS202}
– Rewrite the sentence: “For every student in the class,
that student has studied calculus.”
– Introduce a variable, x: “For every student x in the
class, x has studied calculus.”
– Replace “x has studied calculus” with: C(x)
– Since our domain is all students in CS202, we can
now represent our sentence with: x C(x)

77. Example
• “Every student in this class has studied calculus.”
• Solution 2
– Assume, U = {all people}
– Rewrite the sentence: “For every person x, if x is a
student in the class, then x has studied calculus.”
– Replace “x is a student in the class” with: S(x)
– Replace “x has studied calculus” with: C(x)
– We can now represent our sentence with:
x S(x)  C(x)

78. Example
• Some student in this class has visited Mexico
• Solution 1
– Assume, U = {all students in CS202}
– x M(x)
• Solution 2
– Assume, U = {all people}
– x S(x)  M(x)

79. More Examples
• C(x): x is a CS student
• E(x): x is an MIS student
• S(x): x is a smart student
• U = {all students in CS202}

80. More Examples (Cont..)
• Everyone is a CS student.
x C(x)
• Nobody is an MIS student.
x ~E(x) or ~x E(x)
• All CS students are smart students.
x [C(x)  S(x)]
• Some CS students are smart students.
x [C(x)  S(x)]

81. Quantification of Two Variables
(read left to right)
xyP(x,y) or yxP(x,y)
•True when P(x,y) is true for every pair x,y.
•False if there is a pair x,y for which P(x,y) is false.
xyP(x,y) or yxP(x,y)
True if there is a pair x,y for which P(x,y) is true.
False if P(x,y) is false for every pair x,y.

82. Quantification of Two Variables
xyP(x,y)
•True when for every x there is a y for which P(x,y) is true.
(in this case y can depend on x)
•False if there is an x such that P(x,y) is false for every y.
yxP(x,y)
•True if there is a y for which P(x,y) is true for every x.
(i.e., true for a particular y regardless (or independent) of x)
•False if for every y there is an x for which P(x,y) is false.
Note that order matters here
In particular, if yxP(x,y) is true, then xyP(x,y) is true.
However, if xyP(x,y) is true, it is not necessary that yxP(x,y)
is true.

83. Examples 3a
Let L(x,y) be the statement “x loves y” where U for both
x and y is the set of all people in the world.
Everybody loves Jerry.
xL(x,Jerry)
Everybody loves somebody.
x yL(x,y)
There is somebody whom everybody loves.
yxL(x,y)

84. Examples 3b1
There is somebody whom Lydia does not love.
xL(Lydia,x)
Nobody loves everybody. (For each person there is at
least one person they do not love.)
xyL(x,y)
There is somebody (one or more) whom nobody loves
y x L(x,y)

85. Examples 3b2
There is exactly one person whom everybody loves.
xyL(y,x)?
No. There could be more than one person everybody
loves
x{yL(y,x)  w[(yL(y,w))  w=x]}
If there are, say, two values x1 and x2 (or more) for
which L(y,x) is true, the proposition is false.
x{yL(y,x)  w[(yL(y,w))  w=x]}?
xw[(y L(y,w))  w=x]?

86. Examples 3c
There are exactly two people whom Lynn loves.
x y{xy  L(Lynn,x)  L(Lynn,y)}?
No.
x y{xy  L(Lynn,x)  L(Lynn,y)  z[L(Lynn,z)
(z=x  z=y)]}
Everyone loves himself or herself.
xL(x,x)
There is someone who loves no one besides himself or
herself.
xy(L(x,y)  x=y)

87. Thinking of Quantification as
Loops
Quantifications of more than one variable
can be thought of as nested loops.
•For example, xyP(x,y) can be thought
of as a loop over x, inside of which we
loop over y (i.e., for each value of x).
• Likewise, xyP(x,y) can be thought of
as a loop over x with a loop over y nested
inside. This can be extended to any
number of variables.

88. Quantification as Loops
Using this procedure
•xyP(x,y) is true if P(x,y) is true for all values of x,y
as we loop through y for each value of x.
•xyP(x,y) is true if P(x,y) is true for at least one set of
values x,y as we loop through y for each value of x.
…And so on….

89. Quantification of 3 Variables
Let Q(x,y,z) be the statement “x + y = z”, where x,y,z
are real numbers.
What is the truth values of
•xyzQ(x,y,z)?
•zxyQ(x,y,z)?

90. Quantification of 3 Variables
Let Q(x,y,z) be the statement “x + y = z”, where x,y,z
are real numbers.
•xyzQ(x,y,z)
is the statement, “For all real numbers x and for all
real numbers y, there is a real number z such that
x + y = z.”
True

91. Quantification of 3 Variables
Let Q(x,y,z) be the statement “x + y = z”, where x,y,z
are real numbers.
zxyQ(x,y,z)
is the statement, “There is a real number z such that
for all real numbers x and for all real numbers y,
x + y = z.”
False

92. Examples 4a
Let
P(x) be the statement: “x is a Georgia Tech student”
Q(x) be the statement: “ x is ignorant”
R(x) be the statement: “x wears red”
and U is the set of all people.
No Georgia Tech students are ignorant.
x(P(x) Q(x))
x(P(x) Q(x))
OK by Implication equivalence.
x(P(x)  Q(x))
Does not work. Why?

93. Examples 4a
x(P(x)  Q(x))
x (P(x)  Q(x)) Negation equivalence
x ( P(x)  Q(x)) Implication equivalence
x (  P(x)   Q(x)) DeMorgans
x ( P(x)   Q(x)) Double negation
Only true if everyone is a GT student and is not ignorant.
No Georgia Tech students are ignorant.
x(P(x) Q(x))

94. Examples 4a
P(x) be the statement: “x is a Georgia Tech student”
Q(x) be the statement: “ x is ignorant”
R(x) be the statement: “x wears red”
and U is the set of all people.
No Georgia Tech students are ignorant.
x(P(x)  Q(x))
Also works. Why?

95. Examples 4a
x(P(x)  Q(x))
 x (P(x)  Q(x)) Negation equivalence
x (P(x)  Q(x)) DeMorgan
x (P(x) Q(x)) Implication equivalence
No Georgia Tech students are ignorant.
x(P(x) Q(x))

96. Examples 4b
Let
P(x) be the statement: “x is a Georgia Tech student”
Q(x) be the statement: “ x is ignorant”
R(x) be the statement: “x wears red”
and U is the set of all people.
All ignorant people wear red.
x(Q(x) R(x))

97. Examples 4c
Let
P(x) be the statement: “x is a Georgia Tech student”
Q(x) be the statement: “ x is ignorant”
R(x) be the statement: “x wears red”
and U is the set of all people.
No Georgia Tech student wears red.
x(P(x) R(x))
What about this?
x(R(x)  P(x))

98. Examples 4d
If “no Georgia Tech students are ignorant” and “all
ignorant people wear red”, does it follow that “no
Georgia Tech student wears red?”
x((P(x) Q(x))  (Q(x) R(x)))
NO
Some misguided GT student might wear red!!
This can be shown with a truth table or Wenn diagrams

99. Use implication or conjunction?
• Universal quantifiers usually take implications
• All CS students are smart students.
x [C(x)  S(x)] Correct
x [C(x)  S(x)] Incorrect

100. Use implication or conjunction?
• Existential quantifiers usually take conjunctions
• Some CSE students are smart students.
x [C(x)  S(x)] Correct
x [C(x)  S(x)] Incorrect

101. More Examples
• No CS student is an MIS student.
– If x is a CS student, then that student is not an MIS
student.
x [C(x)  ~E(x)]
– There does not exist a CS student who is also an
MIS student.
~x [C(x)  E(x)]
• If any MIS student is a smart student then he is
also a CS student.
x [(E(x)  S(x))  C(x)]

102. Conclusion
We have covered the following topics in Logic:
Propositional Logic
Propositional Equivalences
Predicates and Quantifiers