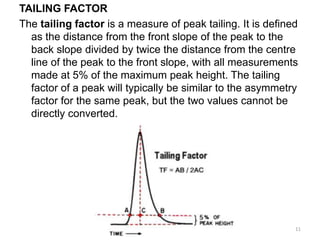
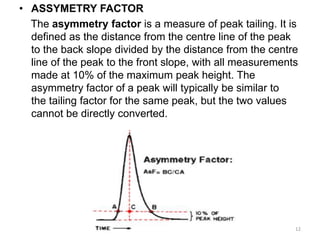
Chromatography is an analytical technique used to separate, identify, and quantify components in complex mixtures. It involves a stationary phase and mobile phase. Components are carried through the stationary phase by the flow of the mobile phase, with separation occurring due to differences in migration rates. Key terms in chromatography include the plate height and number of theoretical plates, which reflect separation efficiency. The Van Deemter equation models how the plate height relates to factors like diffusion and mass transfer between phases, allowing optimization of separation conditions. Chromatography has applications in qualitative and quantitative analysis of sample components.

1. CHROMATOGRAPHY
BY-
RICHA CHAUHAN
AKSHATA ADHYAPAK
1

2. Chromatography is an analytical method that is widely
used for separation, identification and determination
of the chemical components in complex mixtures.
It consist of a mobile phase and stationary phase.
Components of the mixture are carried through the
stationary phase by the flow of gaseous or liquid mobile
phase, separations being based on differences in
migration rates among the sample components.
Chromatographic methods:
 Based on technique:
Column Chromatography (HPLC, GC)
Planar Chromatography (PAPER, TLC)
 Based on affinity:
Adsorption chromatography ( TLC, HPLC, GC)
Partition chromatography ( GLC, PAPER)
 Based on non-affinity:
Gel permeation chromatography 2

3. TERMINOLOGIES
A theoretical plate in many separation processes is a
hypothetical zone or stage in which two phases, such as the
liquid and vapour phases of a substance, establish an
equilibrium with each other.
It is expressed as N,
N= L / H
where N= No. of plates
L= length of column
H= Height equivalent to theoretical plates (HETP)
The plate height H is known as height equivalent of
theoretical plate.
H= ϭ2 / L
where ϭ2 = Variance , L= length of column (cms) 3

4. Plate Theory / Separation Efficiency / Efficiency factor
 It is described as plate height (H) and plate no. (N).
 This is an important characteristic in chromatography as it
reflects no. of times the solute partitions between two phases
while travelling through the column.
 Generally N is expressed as Neffective and given by
Neffective = L / H
 N can also be calculated using following equation
N = (tr’ / wb)2 x 16
where tr’= adjusted retention time
wb = width of peaks
4

5. ISOCRATIC ELUTION: A separation that employs a single solvent or
solvent mixture of constant composition.
GRADIENT ELUTION: Here two or more solvent systems that differ
significantly in polarity are employed. After elution is begun; the ratio of
the solvents is varied in a programmed way, sometimes continuously and
sometimes in a series of steps. Separation efficiency is greatly enhanced
by gradient elution.
To decide whether to go for isocratic or gradient elution, we need to note
the elution of solute with general gradient of mobile phase.
5

6. tg= total time of the
gradient i.e., 18 mins
tg = difference in the
retention time of last peak
and first peak.
In the adjacent diagram,
tg = 13- 3 = 10mins
tg/ tg = 10/18 = 0.8
If this ratio ≥ 0.25, go for
gradient elution
If this ratio ≤ 0.25, go for
isocratic elution
6

7. 7

8. CAPACITY FACTOR
It is used to describe the migration rates of solutes on columns. For a
solute A, the capacity factor k’A is defined as:
k’A = KAVS/VM
where, KA is partition ratio for the species A
VS is the volume of the stationary phase
VM is the volume of the mobile phase
It is a measure of the retention of a peak that is independent of column
geometry or mobile phase flow rate.
k’ = (tr-t0) / t0
tr = retention time of peak
t0= dead time of column
8

9. k’ can be altered by varying stationary phase.
When k’=0 indicates no retention in the stationary phase or no affinity to
the stationary phase
This will lead to no resolution and separation
In such cases alteration in the capacity factor becomes essential to
increase or to get better resolution or separation.
SELECTIVITY FACTOR
It is denoted as α
The selectivity factor of a column for the two species A and B is defined
as
α= KB/KA
KB is the partition ratio for more strongly retained species B and
KA is the constant for less strongly held or more rapidly eluted
species A.
 when α = 1 resolution =0 irrespective of large no of N
 larger α, better and easier separation and resolution
 small changes in α can bring large changes in resolution
9

10.  In case of GC, changes in the stationary phase can bring
large changes in α factor.
 While in case of HPLC α can be changed by changing
both stationary phase and mobile phase.
RESOLUTION
The resolution Rs of a column provides quantitative
measures of its ability to separate two eluted peaks.
It is defined as the difference in the retention times
between two peaks, divided by the combined widths of
elution peaks.
Rs = tr2-tr1
½ (ω1+ω2)
10

11. TAILING FACTOR
The tailing factor is a measure of peak tailing. It is defined
as the distance from the front slope of the peak to the
back slope divided by twice the distance from the centre
line of the peak to the front slope, with all measurements
made at 5% of the maximum peak height. The tailing
factor of a peak will typically be similar to the asymmetry
factor for the same peak, but the two values cannot be
directly converted.
11

12. • ASSYMETRY FACTOR
The asymmetry factor is a measure of peak tailing. It is
defined as the distance from the centre line of the peak
to the back slope divided by the distance from the centre
line of the peak to the front slope, with all measurements
made at 10% of the maximum peak height. The
asymmetry factor of a peak will typically be similar to
the tailing factor for the same peak, but the two values
cannot be directly converted.
12

13. Rate Theory
In the rate theory, a number of different peak dispersion
processes were proposed and expressions were developed
that described
• the contribution of each of the processes to the total
variance of the eluted peak
• the final equation that gave an expression for the variance
per unit length of the column
The rate theory has resulted in a number of different equations
All such equations give a type of hyperbolic function that predicts
a minimum plate height at an optimum velocity and, thus, a
maximum efficiency. At normal operating velocities it has been
demonstrated that the Van Deemter equation gives the best fit
to experimental data
The Van Deemter Equation
H = A + B/u + u [CM + CS] 13

14. H = A + B/u + u [CM +CS]
Van Deemter model
u = L/ tM
A: random movement through stationary phase
B: diffusion in mobile phase
C: interaction with stationary phase
H: plate height
u: average linear velocity
14

15. Term A
- molecules may travel
unequal distances
- independent of u
- depends on size of
stationary particles or
coating (TLC)
H = A + B/u + u [CM +CS]
Van Deemter model
time
Eddy diffusion
MP moves through the column
which is packed with stationary
phase. Solute molecules will take
different paths through the
stationary phase at random. This
will cause broadening of the solute
band, because different paths are
of different lengths.
15

16. Term B
H = A + B/u + u [CM +CS]
Van Deemter model
Longitudinal diffusion
B = 2γ DM
γ: Impedance factor due to
packing
DM: molecular diffusion
coefficient
B term dominates at low u, and
is more important in GC than LC
since DM(gas) > 104 DM(liquid)
One of the main causes
of band spreading is
DIFFUSION
The diffusion coefficient
measures the ratio at
which a substance
moves randomly from a
region of higher
concentration to a region
of lower concentration
16

17. Term B
H = A + B/u + u [CM +CS]
Van Deemter model
Longitudinal diffusion
B = 2γ DM
γ: Impedance factor due to
packing
DM: molecular diffusion
coefficient
B term dominates at low u and
is more important in GC than LC
since DM(gas) > 104 DM(liquid)
B - Longitudinal diffusion
The concentration of analyte is less
at the edges of the band than at the
centre. Analyte diffuses out from the
centre to the edges. This causes
band broadening. If the velocity of
the mobile phase is high then the
analyte spends less time in the
column, which decreases the effects
of longitudinal diffusion.
17

18. Cs: stationary phase-mass transfer
Cs = [(df)2]/Ds
df: stationary phase film thickness
Ds: diffusion coefficient of analyte in SP
CM: mobile phase–mass transfer
CM = [(dP)2]/DM packed columns
CM = [(dC)2]/DM open columns
H = A + B/u + u [CM +CS]
Van Deemter model
Term C
dP: particle diameter
dC: column diameter
Bandwidth
Stationary
phase
Mobile
phase
Elution
Broadened bandwidth
Slow
equilibration
18

19. H = A + B/u + u [CM +CS]
Van Deemter model
Term C (Resistance to mass transfer) Bandwidth
Stationary
phase
Mobile
phase
Elution
Broadened bandwidth
Slow
equilibration
The analyte takes a certain amount of time to equilibrate
between the stationary and mobile phase. If the velocity of the
mobile phase is high, and the analyte has a strong affinity for
the stationary phase, then the analyte in the mobile phase will
move ahead of the analyte in the stationary phase. The band
of analyte is broadened. The higher the velocity of mobile
phase, the worse the broadening becomes. 19

20. Van Deemter plot
A plot of plate height vs average linear velocity of mobile
phase
Such plot is of considerable use in determining the optimum
mobile phase flow rate
A
B
C
20

21. • APPLICATIONS OF CHROMATOGRAPHY
Qualitative analysis: to determine presence or absence of
components in mixtures that contain a limited number of
species.
Quantitative analysis:
It is based upon a comparison of either the height or the
area of an analyte peak with that of one or more standards.
Both of these parameters vary linearly with concentrations.
21

22. • REFERENCES:
• D. A. Skoog and J. J. Leary, principles of instrumental
analysis, 4th edition, page no. 592-598, 1992.
• Chromatography: fundamentals and applications of
chromatography and electrophoretic methods, E.
Heftmann, New York, Elsevier, 1983
• Chromatographic theory and basic principles, J. A.
Jonsson, New York, 1987
• www.lcresources.com
22

23. THANK YOU
23