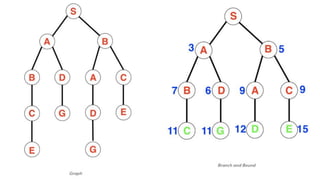
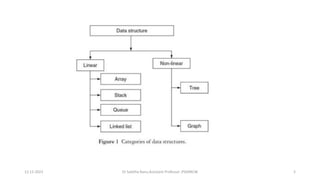
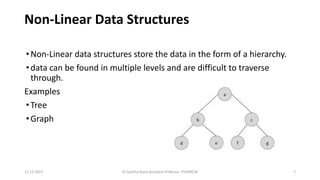
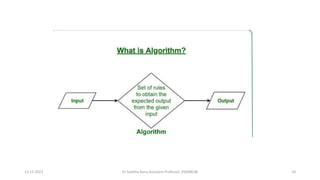
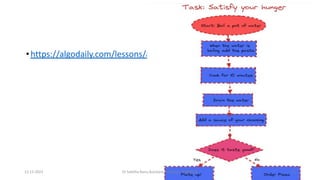
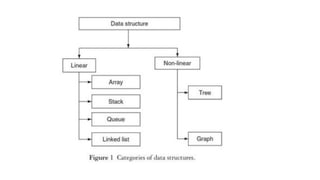
The document outlines a course on data structures and algorithms, covering concepts such as arrays, stacks, queues, linked lists, trees, and graphs, along with their operations and applications. It includes an introduction to algorithm specifications, performance analysis, and various types of data structures, both linear and non-linear. Additionally, it discusses algorithms' characteristics, advantages, disadvantages, and comparisons between stacks and queues, along with their implementations.















![Arrays
•fixed-size sequenced collection of variables belonging to the same data types
and stored in contiguous memory.
•Set of pairs, index or value
•The array has adjacent memory locations to store values.
•convenient structure for representing data
•Two terms to understand the concept of array are Element and Index
✔ Element − Each item stored in an array is called an element.
✔ Index − Each location of an element in an array has a numerical index, which is used to
identify the element.
data_type array_name [array_size];
12-12-2023 Dr Sabitha Banu,Assistant Professor ,PSGRKCW 20](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-20-320.jpg)

![Ordered Lists
• list in which the elements must always be ordered in a particular way
• Also called as Sorted list.
Eg. (SUNDAY ,MONDAY, TUESDAY, WEDNESDAY, THURSDAY, FRIDAY,
SATURDAY)
Representation of arrays
✔ One dimensional array
❖ A one-dimensional array is also called a single dimensional array where the elements will be accessed in
sequential order. This type of array will be accessed by the subscript of either a column or row index. eg
a[n] or an
✔ Two dimensional array
❖ When the number of dimensions specified is more than one, then it is called as a
multi-dimensional array. Eg a[3,3] (row x column)
12-12-2023 Dr Sabitha Banu,Assistant Professor ,PSGRKCW 22](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-22-320.jpg)
![Eg a[3][4]
• A two-dimensional array will be accessed by using the subscript of row and column
index.
eg a[1][1]
12-12-2023 Dr Sabitha Banu,Assistant Professor ,PSGRKCW 23](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-23-320.jpg)
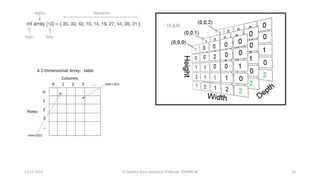
![1D or one dimensional array-
•A list of items having one variable name with only one subscript
•Computer reserves 5 storage locations
•Int number[5]={35,40,20,57,19}
12-12-2023 Dr Sabitha Banu,Assistant Professor ,PSGRKCW 25](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-25-320.jpg)
![12-12-2023 Dr Sabitha Banu,Assistant Professor ,PSGRKCW 26
Char name[10]=“well done”;
When declaring a character arrays ,allocate one extra element space
for the null terminator
When a compiler reads a character arrays it terminates with the
additional null character(‘0’)](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-26-320.jpg)




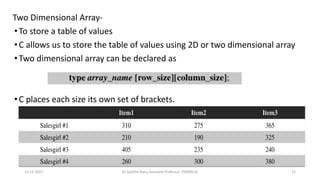
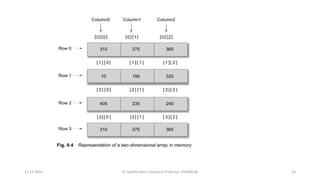



![Memory Layout-
•The subscripts in the 2d arrays represents the rows and columns
•The elements of the array are stored contiguously in increasing memory
locations.
•Starts to store row wise ,starting from the first row and ending with the last
row, treating each row like a simple array.
12-12-2023 Dr Sabitha Banu,Assistant Professor ,PSGRKCW 37
A[3][3]={{10,20,30},{40,50,60},{70,80,
90}};](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-37-320.jpg)

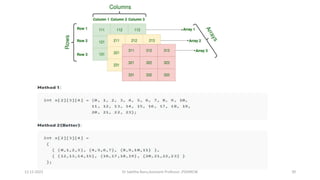
















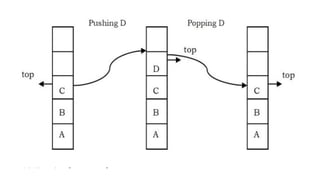



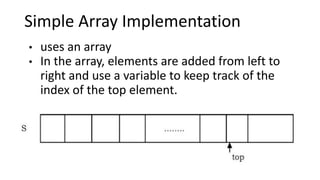



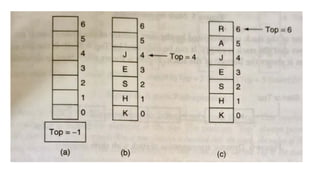





![❖ Suppose there is an array STACK[n] divided into two stack STACK A
and STACK B, where n = 10.
➢ STACK A expands from the left to the right, i.e., from 0th
element.
➢ STACK B expands from the right to the left, i.e., from 10th
element.
➢ The combined size of both STACK A and STACK B never
exceeds 10.](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-73-320.jpg)

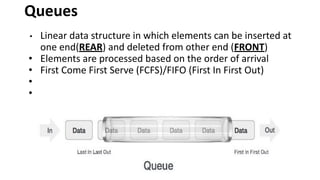

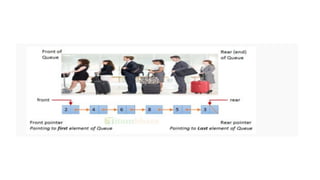
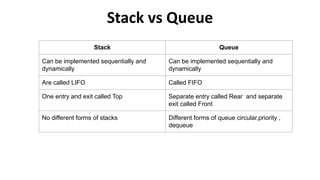
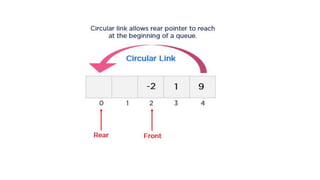
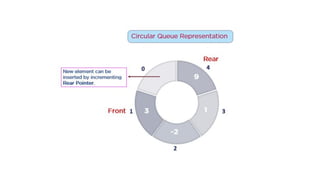
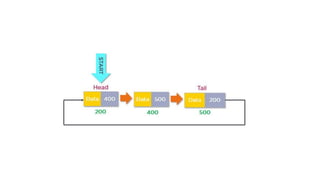
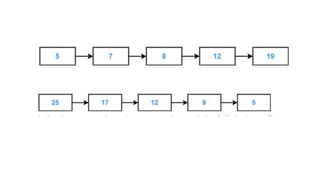
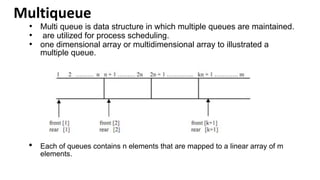
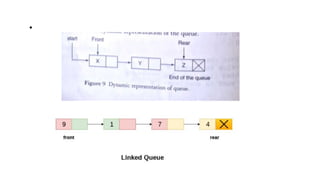
![Array representation
• A queue is implemented with max elements
array stored from queue[i] to queue[j],Max
• I,j are front(F) and Rear(R)
• Contains two pointer variables
• Front -location of the front element of the queue
• Rear-location of the rear element of the queue](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-78-320.jpg)






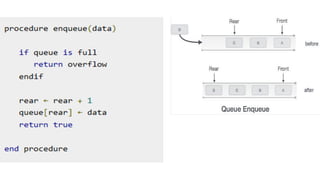





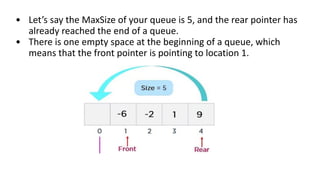
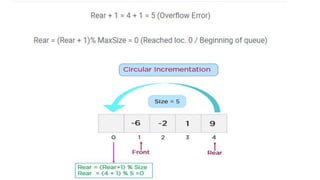
![Enqueue(x) Operation
Step 1: Check if the queue is full (Rear + 1 % Maxsize = Front)
Step 2: If the queue is full, there will be an Overflow error
Step 3: Check if the queue is empty, and set both Front and Rear
to 0
Step 4: If Rear = Maxsize - 1 & Front != 0 (rear pointer is at the
end of the queue and front is not at 0th index), then set Rear = 0
Step 5: Otherwise, set Rear = (Rear + 1) % Maxsize
Step 6: Insert the element into the queue (Queue[Rear] = x)
Step 7: Exit](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-102-320.jpg)


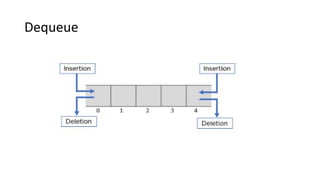
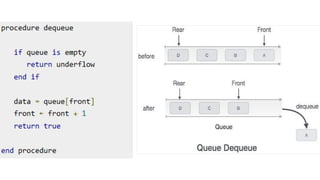
![Dequeue() Operation
Step 1: Check if the queue is empty (Front = -1 & Rear = -1)
Step 2: If the queue is empty, Underflow error
Step 3: Set Element = Queue[Front]
Step 4: If there is only one element in a queue, set both Front
and Rear to -1 (IF Front = Rear, set Front = Rear = -1)
Step 5: And if Front = Maxsize -1 set Front = 0
Step 6: Otherwise, set Front = Front + 1
Step 7: Exit](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-106-320.jpg)





















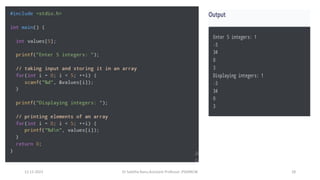
![#include <stdio.h>
int MAXSIZE = 8;
int stack[8];
int top = -1;
/* Check if the stack is empty */
int isempty(){
if(top == -1)
return 1;
else
return 0;
}
/* Check if the stack is full */
int isfull(){
if(top == MAXSIZE)
return 1;
else
return 0;
}
/* Function to return the
topmost element in the stack */
int peek(){
return stack[top];
}](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-137-320.jpg)
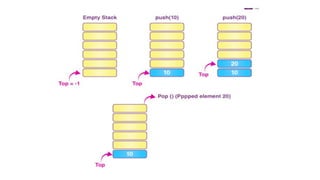
![/* Function to delete from the stack
*/
int pop(){
int data;
if(!isempty()) {
data = stack[top];
top = top - 1;
return data;
} else {
printf("Could not retrieve data,
Stack is empty.n");
}
}
/* Function to insert into the stack
*/
int push(int data){
if(!isfull()) {
top = top + 1;
stack[top] = data;
} else {
printf("Could not insert data,
Stack is full.n");
}
}](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-138-320.jpg)



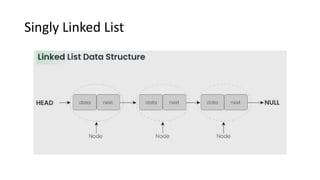




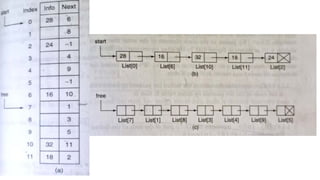

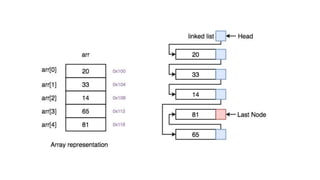
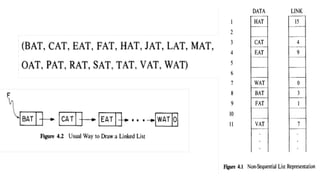
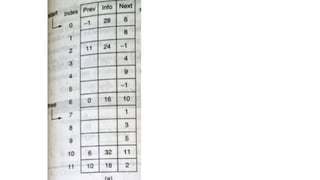
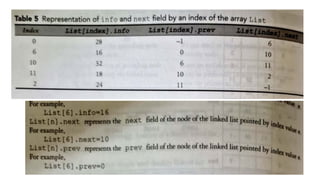
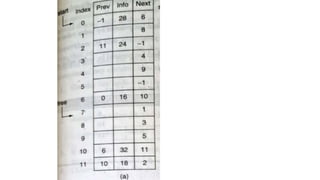
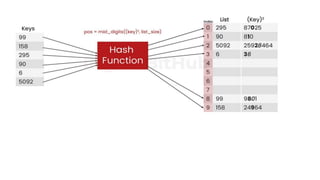
![List[n] -number of nodes in the list
List[6].info=16
List[6].field=10](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-149-320.jpg)

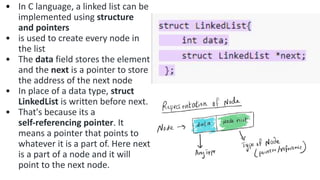















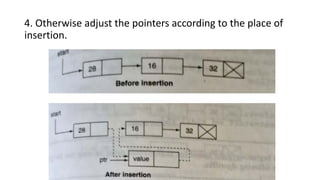
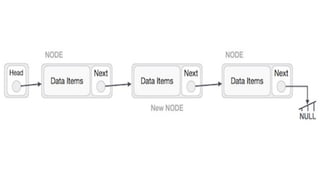


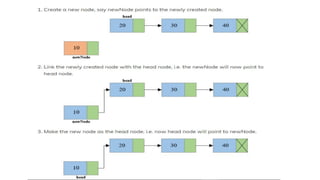

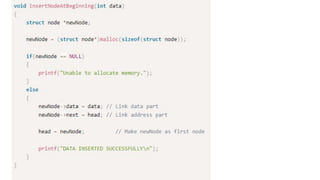

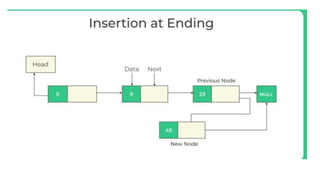

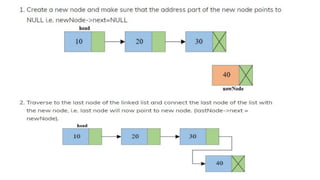
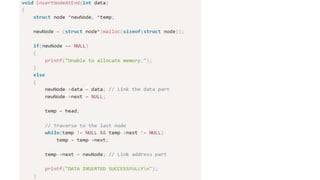


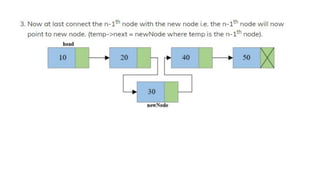



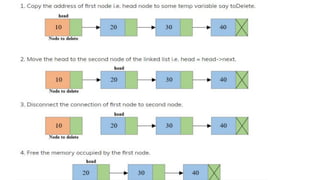
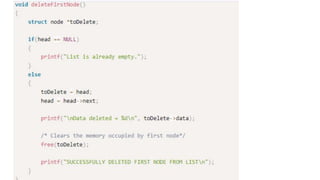

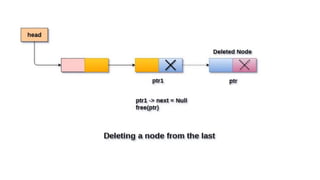
![Step 1: IF HEAD = NULL
Write UNDERFLOW
Go to Step 8
[END OF IF]
Step 2: SET PTR = HEAD
Step 3: Repeat Steps 4 and 5 while PTR ->
NEXT!= NULL
Step 4: SET PREPTR = PTR
Step 5: SET PTR = PTR -> NEXT
[END OF LOOP]
Step 6: SET PREPTR -> NEXT = NULL
Step 7: FREE PTR
Step 8: EXIT](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-196-320.jpg)

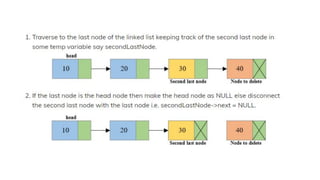
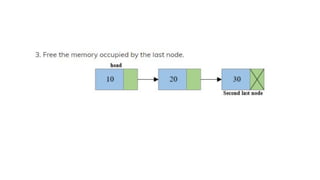




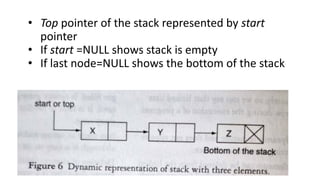
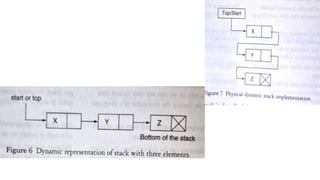


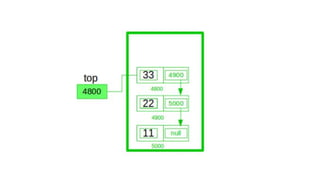







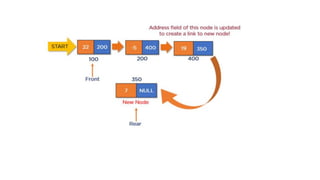

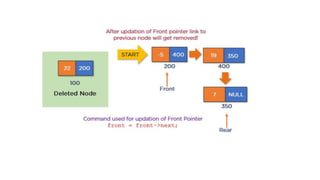
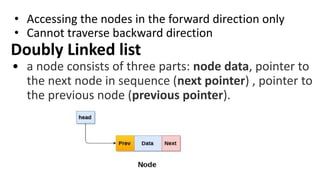
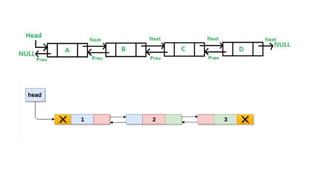
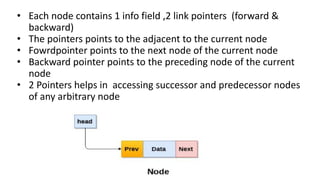
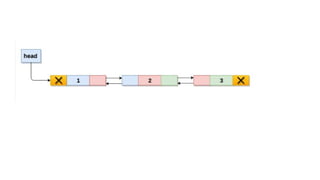
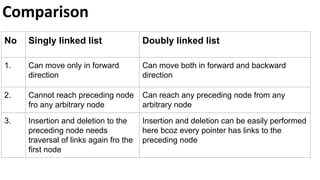


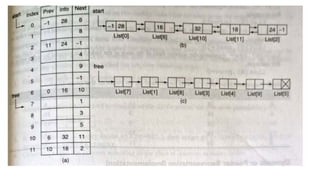


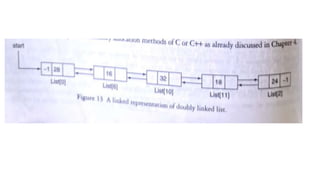


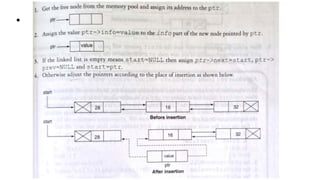
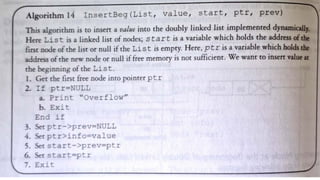

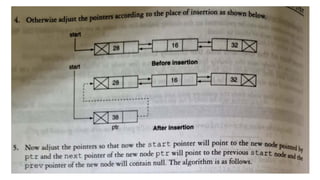
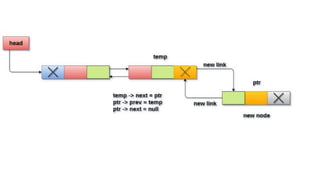
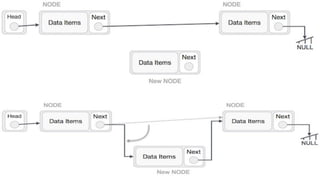
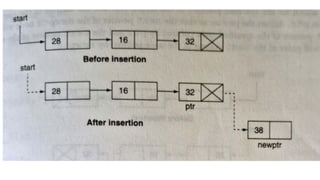
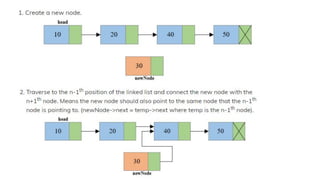
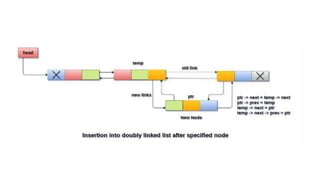
![Insert to the end of DLL
Algorithm
○ Step 1: IF PTR = NULL
○ Write OVERFLOW
Go to Step 11
[END OF IF]
○ Step 2: SET NEW_NODE = PTR
○ Step 3: SET PTR = PTR -> NEXT
○ Step 4: SET NEW_NODE -> DATA = VAL
○ Step 5: SET NEW_NODE -> NEXT = NULL
○ Step 6: SET TEMP = START
○ Step 7: Repeat Step 8 while TEMP
-> NEXT != NULL
○ Step 8: SET TEMP = TEMP ->
NEXT
○ [END OF LOOP]Step 9: SET TEMP
-> NEXT = NEW_NODE
○ Step 10C: SET NEW_NODE ->
PREV = TEMP
○ Step 11: EXIT](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-242-320.jpg)

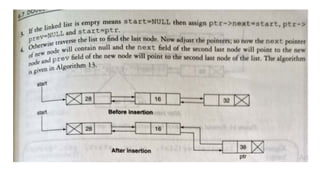
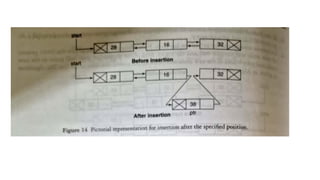
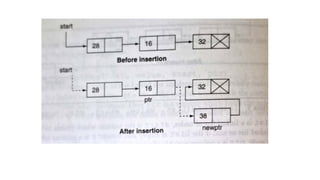
![Insert after in DLL
○ Step 1: IF PTR = NULL
○ Write OVERFLOW
Go to Step 15
[END OF IF]Step 2: SET NEW_NODE =
PTR
○ Step 3: SET PTR = PTR -> NEXT
○ Step 4: SET NEW_NODE -> DATA = VAL
○ Step 5: SET TEMP = START
○ Step 6: SET I = 0
○ Step 7: REPEAT 8 to 10 until I
○ Step 8: SET TEMP = TEMP -> NEXT
○ STEP 9: IF TEMP = NULL
○ STEP 10: WRITE "LESS THAN DESIRED NO. OF
ELEMENTS"
○ GOTO STEP 15
[END OF IF]
[END OF LOOP]Step 11: SET NEW_NODE ->
NEXT = TEMP -> NEXT
○ Step 12: SET NEW_NODE -> PREV = TEMP
○ Step 13 : SET TEMP -> NEXT = NEW_NODE
○ Step 14: SET TEMP -> NEXT -> PREV =
NEW_NODE
○ Step 15: EXIT](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-246-320.jpg)



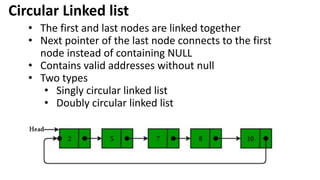

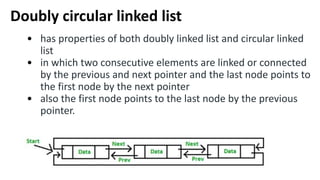

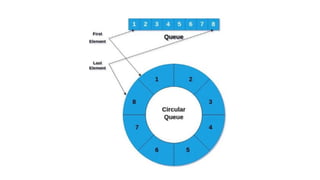

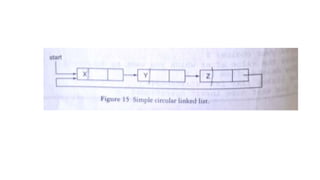


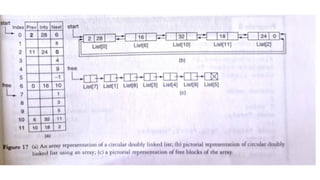


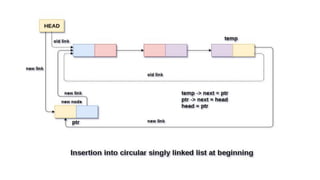
![Insertion into circular singly linked list at beginning
Step 1: IF PTR = NULL
Write OVERFLOW
Go to Step 11
[END OF IF]
Step 2: SET NEW_NODE = PTR
Step 3: SET PTR = PTR -> NEXT
Step 4: SET NEW_NODE -> DATA = VAL
Step 5: SET TEMP = HEAD
Step 6: Repeat Step 8 while TEMP -> NEXT !=
HEAD
Step 7: SET TEMP = TEMP -> NEXT
[END OF LOOP]
Step 8: SET NEW_NODE -> NEXT = HEAD
Step 9: SET TEMP → NEXT = NEW_NODE
Step 10: SET HEAD = NEW_NODE
Step 11: EXIT](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-263-320.jpg)




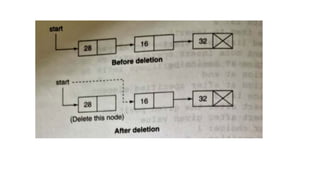
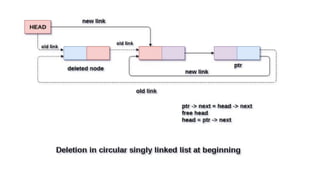
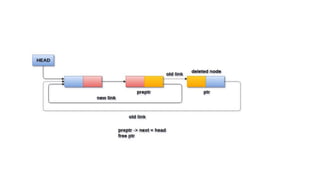
![Deletion in circular singly linked list at beginning
Step 1: IF HEAD = NULL
Write UNDERFLOW
Go to Step 8
[END OF IF]Step 2: SET PTR = HEAD
Step 3: Repeat Step 4 while PTR → NEXT !=
HEAD
Step 4: SET PTR = PTR → next
[END OF LOOP]
Step 5: SET PTR → NEXT =
HEAD → NEXT
Step 6: FREE HEAD
Step 7: SET HEAD = PTR →
NEXT
Step 8: EXIT](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-270-320.jpg)

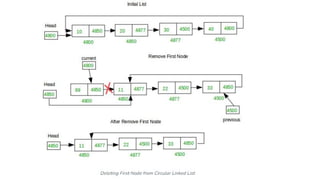
![Deletion in Circular singly linked list at the end
Step 1: IF HEAD = NULL
Write UNDERFLOW
Go to Step 8
[END OF IF]Step 2: SET PTR = HEAD
Step 3: Repeat Steps 4 and 5 while PTR -> NEXT != HEAD
Step 4: SET PREPTR = PTR
Step 5: SET PTR = PTR -> NEXT
[END OF LOOP]Step 6: SET PREPTR -> NEXT = HEAD
Step 7: FREE PTR
Step 8: EXIT](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-275-320.jpg)




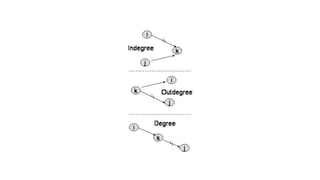



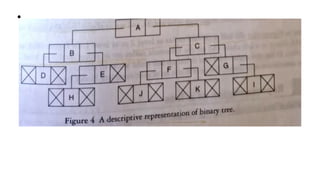


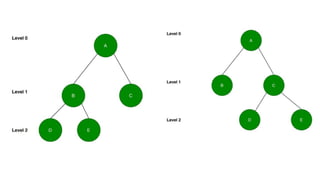
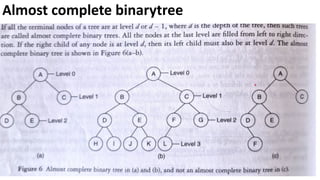
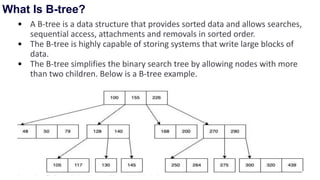

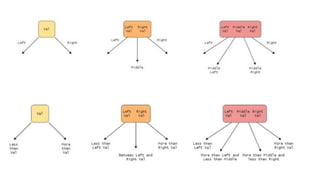

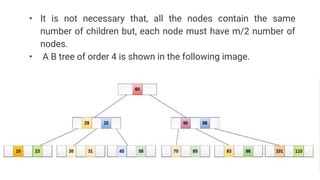

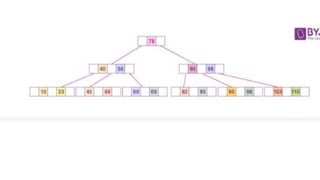

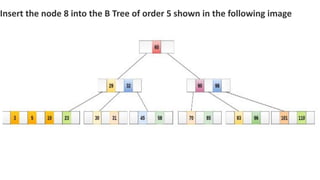
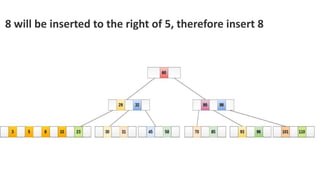
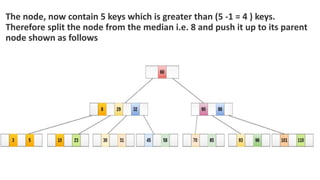


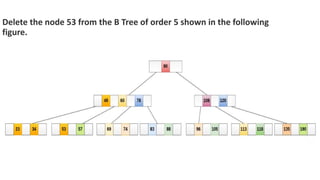


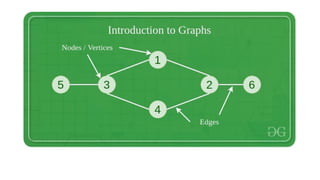


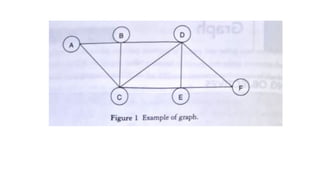

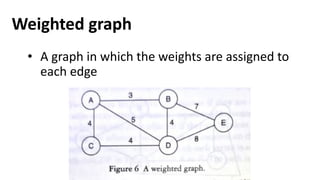
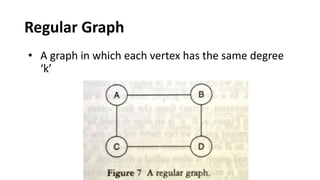
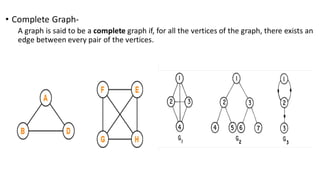
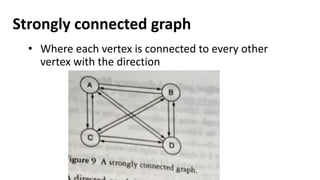
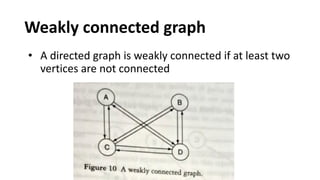
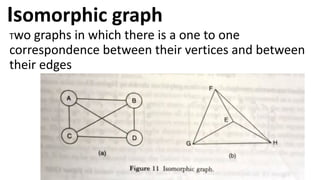

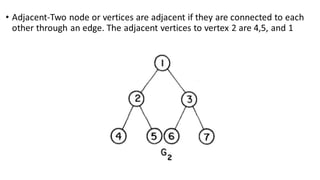
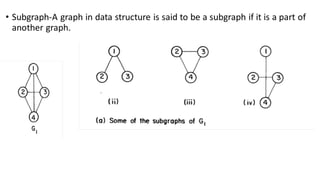

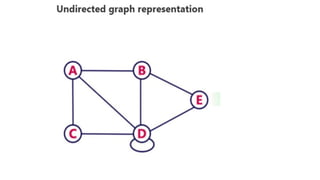
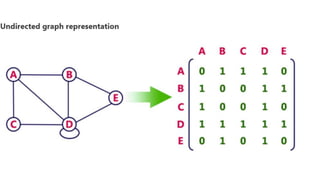
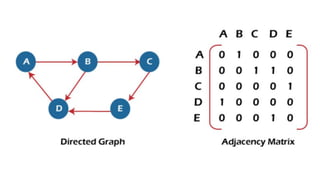
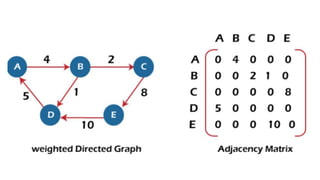
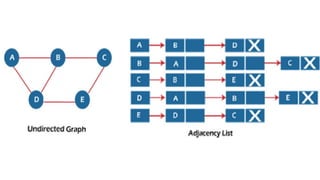
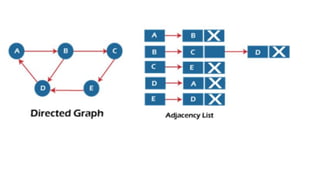
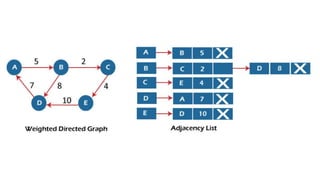
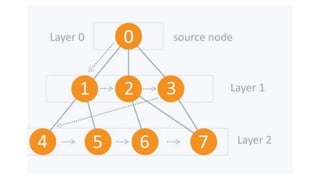
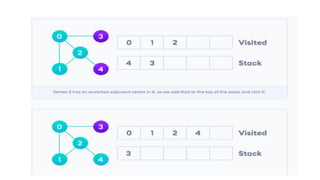
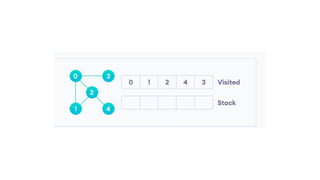
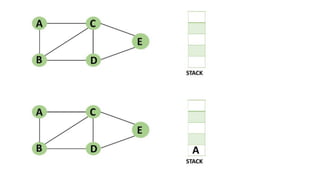
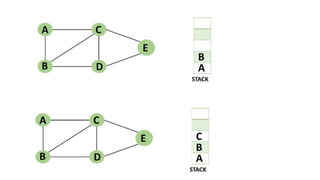
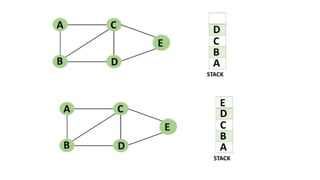
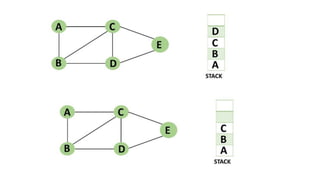
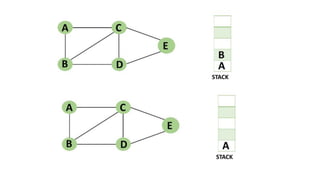
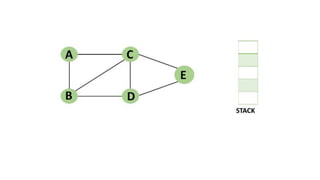
![Sequential representation using adjacency matrix
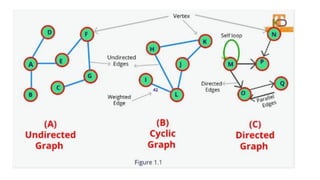
• use of an adjacency matrix to represent the mapping between vertices and edges of the graph.
• adjacency matrix can be used to represent the undirected graph, directed graph, weighted directed graph,
and weighted undirected graph.
• If adj[i][j] = w, it means that there is an edge exists from vertex i to vertex j with weight w.
• An entry Aij
in the adjacency matrix representation of an undirected graph G will be 1 if an edge exists
between Vi
and Vj
.
• If an Undirected Graph G consists of n vertices, then the adjacency matrix for that graph is n x n, and the
matrix A = [aij] can be defined as -
• aij
= 1 {if there is a path exists from Vi
to Vj
}
• a = 0 {Otherwise}](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-329-320.jpg)






























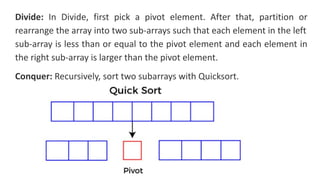
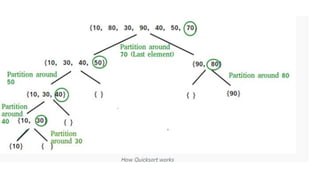
![function quickSort(arr):
if length(arr) <= 1:
return arr
else:
pivot = selectPivot(arr) // Choose pivot element
left = [elements in arr less than pivot]
right = [elements in arr greater than pivot]
return concatenate(quickSort(left), pivot,
quickSort(right))](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-371-320.jpg)




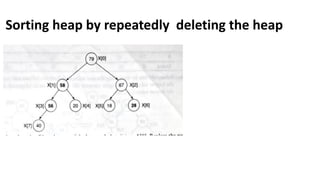
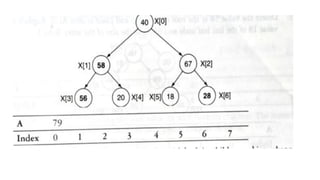
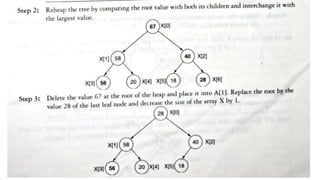
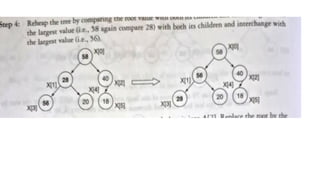
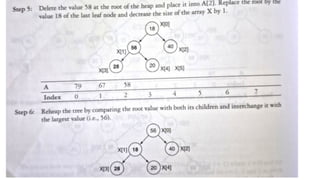




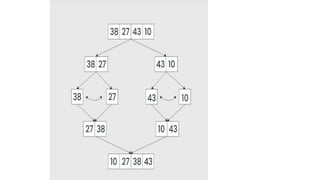
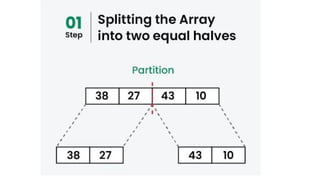
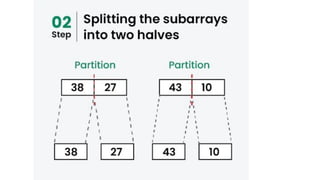
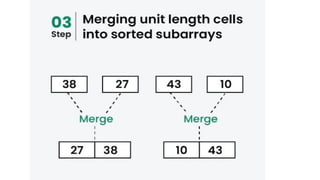
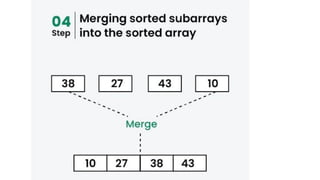
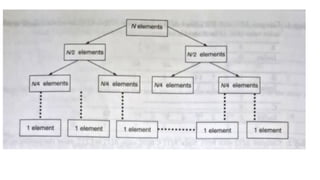










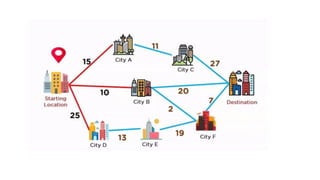




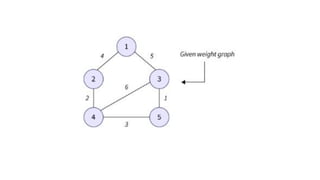





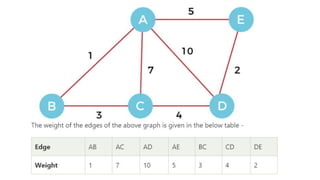
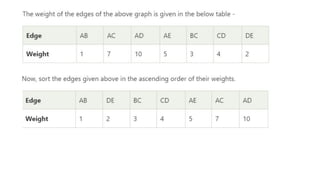
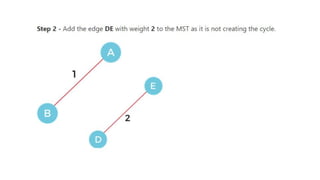
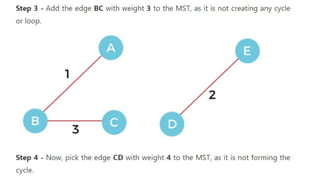
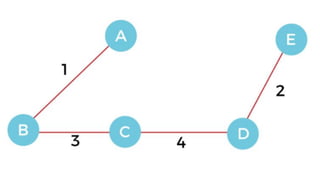

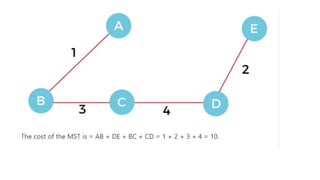


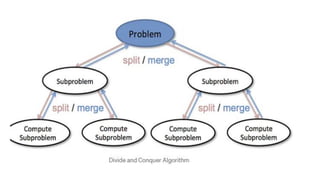








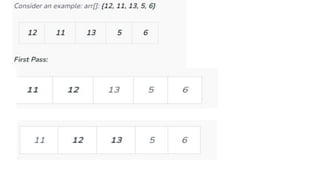
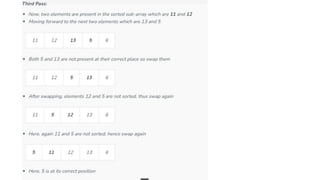
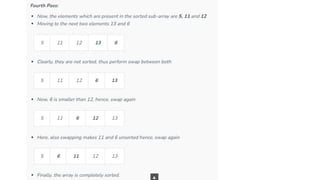
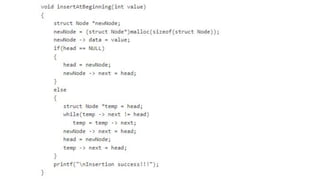
![1. defines a function named insertion_sort that takes a single
argument arr, which is expected to be a list.
2. calculates the length of the input list arr and assigns it to
the variable n.
3. initiates a loop that iterates over the indices of the list
arr starting from index 1 up to (but not including) n.
4. selects the current element (key) at index i from the list
arr. This element will be compared and inserted into its
correct position in the sorted sublist.
5. initializes a variable j to the index directly before i. j will
be used to traverse the sorted sublist from right to left
to find the correct position for key.
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] >
key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-439-320.jpg)
![1. starts a while loop that continues as
long as j is greater than or equal to 0
(ensuring we don't go out of bounds
of the list) and the element at index j
is greater than the key value. This loop
moves elements of the sorted sublist
greater than key one position to the
right.
2. Within the while loop, these two lines
shift elements of the sorted sublist to
the right to make space for the key
element. j is decremented to continue
traversing the sorted sublist.
3. nce the correct position for key is
found (either at index j+1 or 0 if j
becomes -1), key is inserted into the
sorted sublist at index j+1.
def insertion_sort(arr):
n = len(arr)
for i in range(1, n):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] >
key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-440-320.jpg)














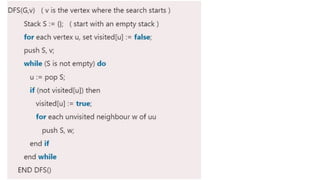

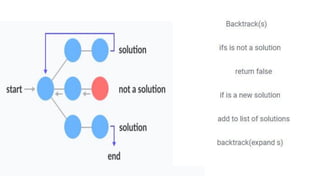

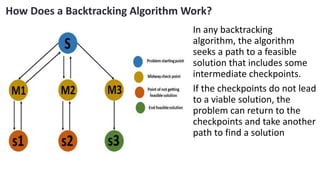

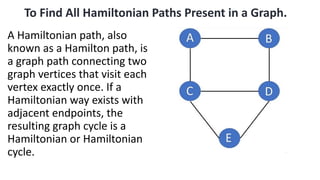
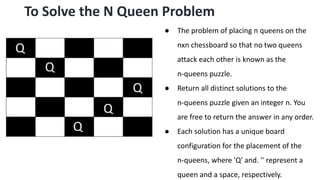

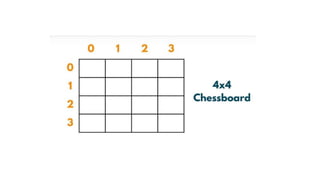

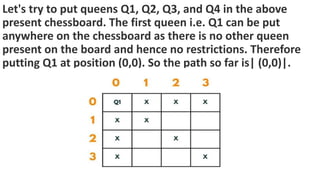
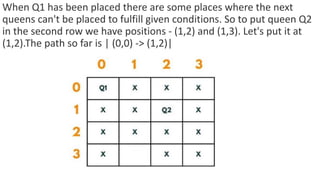
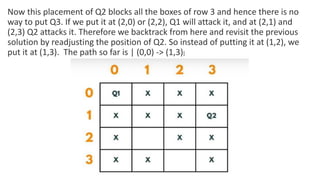
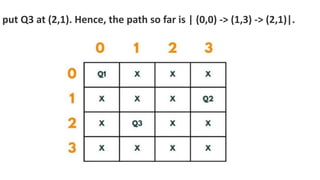
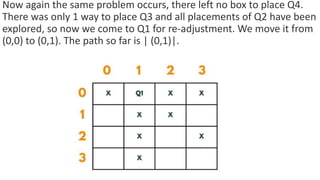
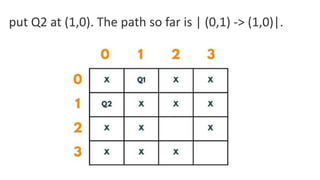
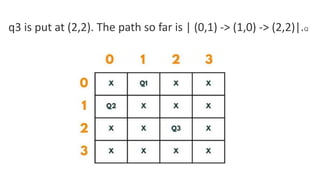
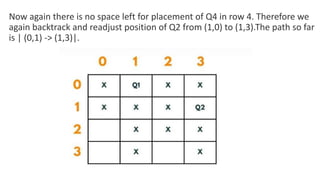
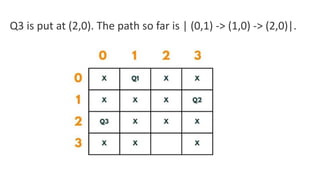
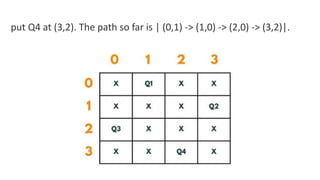
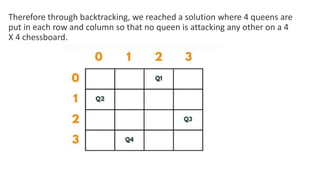

![5. If the cell is safe, we put 'Q' in that row and column of the board
and again call the solve function by incrementing the column by 1.
6. Whenever we reach a position where the column becomes
equal to board length, this implies that all the columns and possible
arrangements have been explored, and so we return.
7. Coming on to the boolean isSafe() function, we check if a queen
is already present in that row/ column/upper left diagonal/lower
left diagonal/upper right diagonal /lower right diagonal. If the
queen is present in any of the directions, we return false. Else we
put board[row][col] = 'Q' and return true.](https://image.slidesharecdn.com/datastructureandalgorithm-in23c051-240421155926-9e814639/85/DATA-STRUCTURE-AND-ALGORITHM-for-beginners-490-320.jpg)