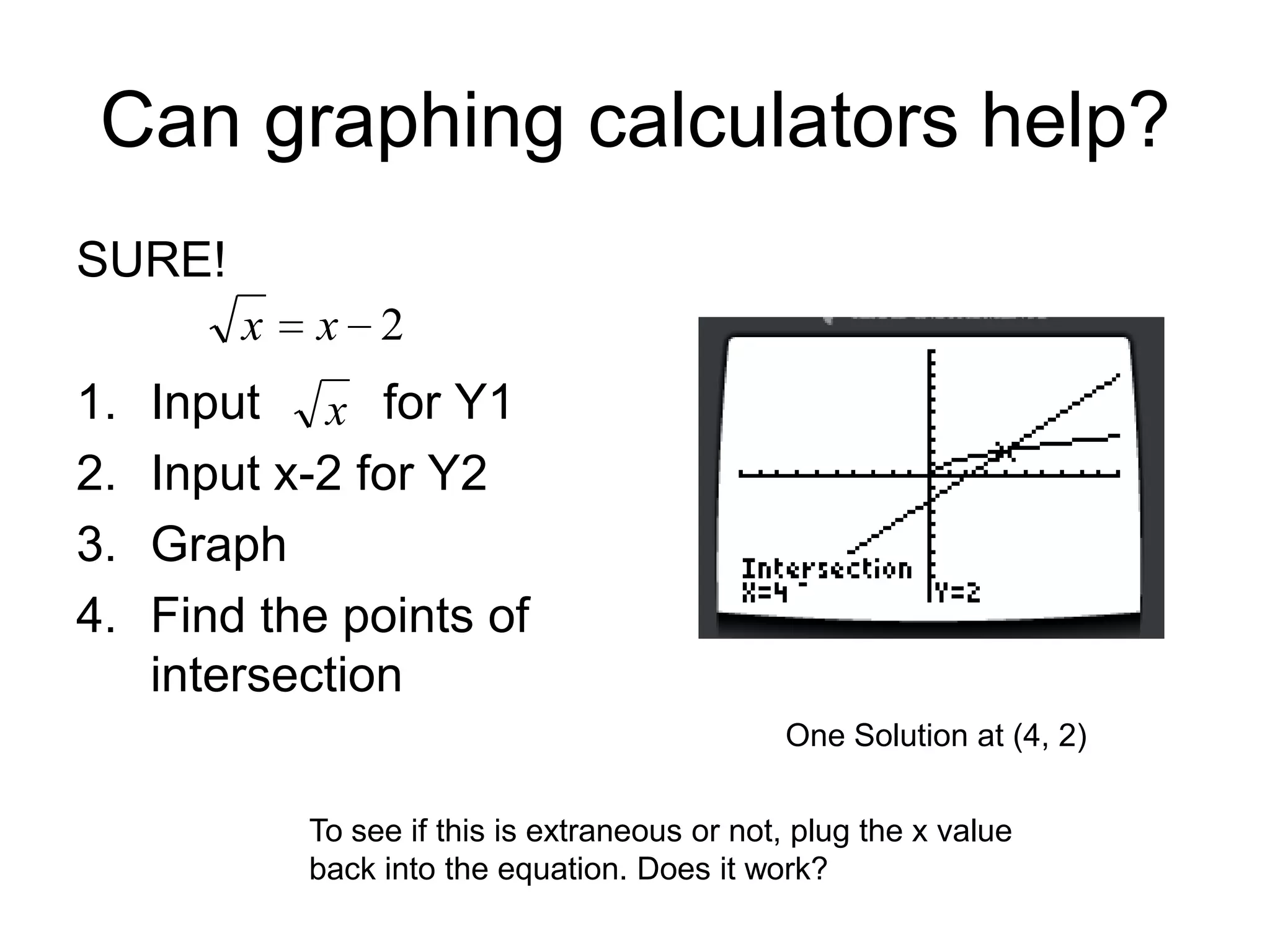
This document provides steps for solving radical equations: 1) Isolate the radical on one side of the equation by performing inverse operations 2) Raise both sides of the equation to a power equal to the index of the radical to eliminate the radical 3) Solve the remaining polynomial equation It includes examples of solving simpler radical equations as well as more complex equations involving fractions and multiple radicals. Checking solutions is emphasized as extraneous solutions may occasionally occur. Graphing calculators can also help visualize and find solutions to radical equations.

1. 7.7 Solving Radical Equations
p.453

2. What is a Radical Expression?
• A Radical Expression
is an equation that
has a variable in a
radicand or has a
variable with a
rational exponent.
3
x 10
2
3
yes
25
yes
3 x 10
no
( x 2)

3. Steps to solve a radical equation:
STEP 1: Isolate the radical on one side of the equation
(if possible)
STEP 2: Raise each side of the equation to a power equal to the
index of the radical to eliminate the radical
STEP 3: Solve the remaining polynomial equation.
CHECK YOUR RESULTS.

4. EXAMPLE – Solving a Radical
Equation
5x 1 6 0
5x 1 6
2
2
5x 1 (6 )
5x 1 36
5x 35
x 7
Square both sides to get rid of
the square root

5. EXAMPLE
x 15
3
x
2
2
x 15 (3
x 15 (3
x 15
24
3
16
x)
x )(3
9 6 x
15
16 15
x)
x
NO SOLUTION
Since 16 doesn’t plug in
as a solution.
9 6 x
6 x
4
x
16 x
1 3 4
1 1
Let’s Double Check
that this works
Note: You will get
Extraneous
Solutions from time
to time – always do
a quick check

6. Let’s Try Some
2
3x 2
6
2( x 2)
2
3
50

7. Let’s Try Some
2
3x 2
6
2( x 2)
2
3
50

8. SOLVING MORE COMPLEX
EQUATIONS
4( x 1)
2
101
20
2
4( x 1)
2
( x 1)
( x 1)
+ because we
are taking an
even power
(square root)
of both sides
81
81
( x 1) i
( x 1)
( x 1)
9i
x 1
9i
2
2
4
81
4
81
1
4
i 92
9i
2
1
9i
2

9. RADICAL EQUATIONS
3(5n 1)
1
3
2
3(5n 1)
1
3
2
1
3
(5n 1)
1 3
(5n 1) 3
(5n 1)
5n
5n
8
0
2
8
27
5n
RAISE BOTH SIDES
TO RECIPROCAL POWER
3
2
27
8
ISOLATE RADICAL / RATIONAL
3
3
SOLVE FOR THE VARIABLE
27
1
27
35
27
27
n
7
27

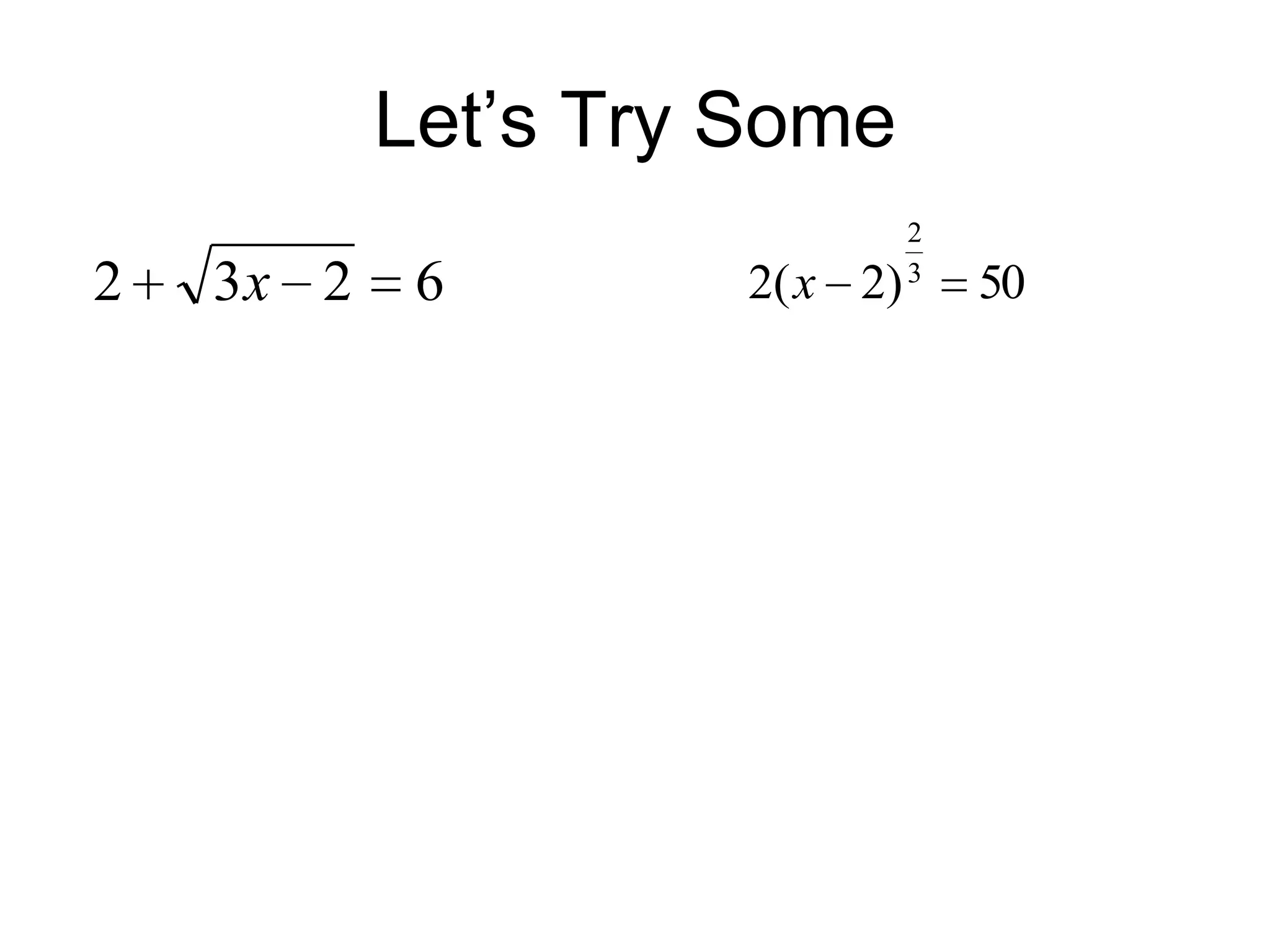
10. SOLVING MORE COMPLEX
EQUATIONS
(2 x 1)
0.5
(3x 4)
0.25
0
0.5
0.25
(2 x 1)
(3x 4)
0.5 4
0.25 4
[( 2 x 1) ] [(3x 4) ]
2
(2 x 1) 3 x 4
4x
2
4 x 1 3x 4
4x
2
Raise each side to the 4th
power. This will get you
integer powers – much
easier to work with!
x
x 3 0
3
, 1
4
Factor

11. Let’s Try Some . . . check for
extraneous solutions
(2 x 1)
0.5
(3x 4)
0.25
0

12. Let’s Try Some . . . check for
extraneous solutions
(2 x 1)
0.5
(3x 4)
0.25
0
x
3
, 1
4

13. Can graphing calculators help?
SURE!
x
1.
2.
3.
4.
x 2
Input x for Y1
Input x-2 for Y2
Graph
Find the points of
intersection
One Solution at (4, 2)
To see if this is extraneous or not, plug the x value
back into the equation. Does it work?