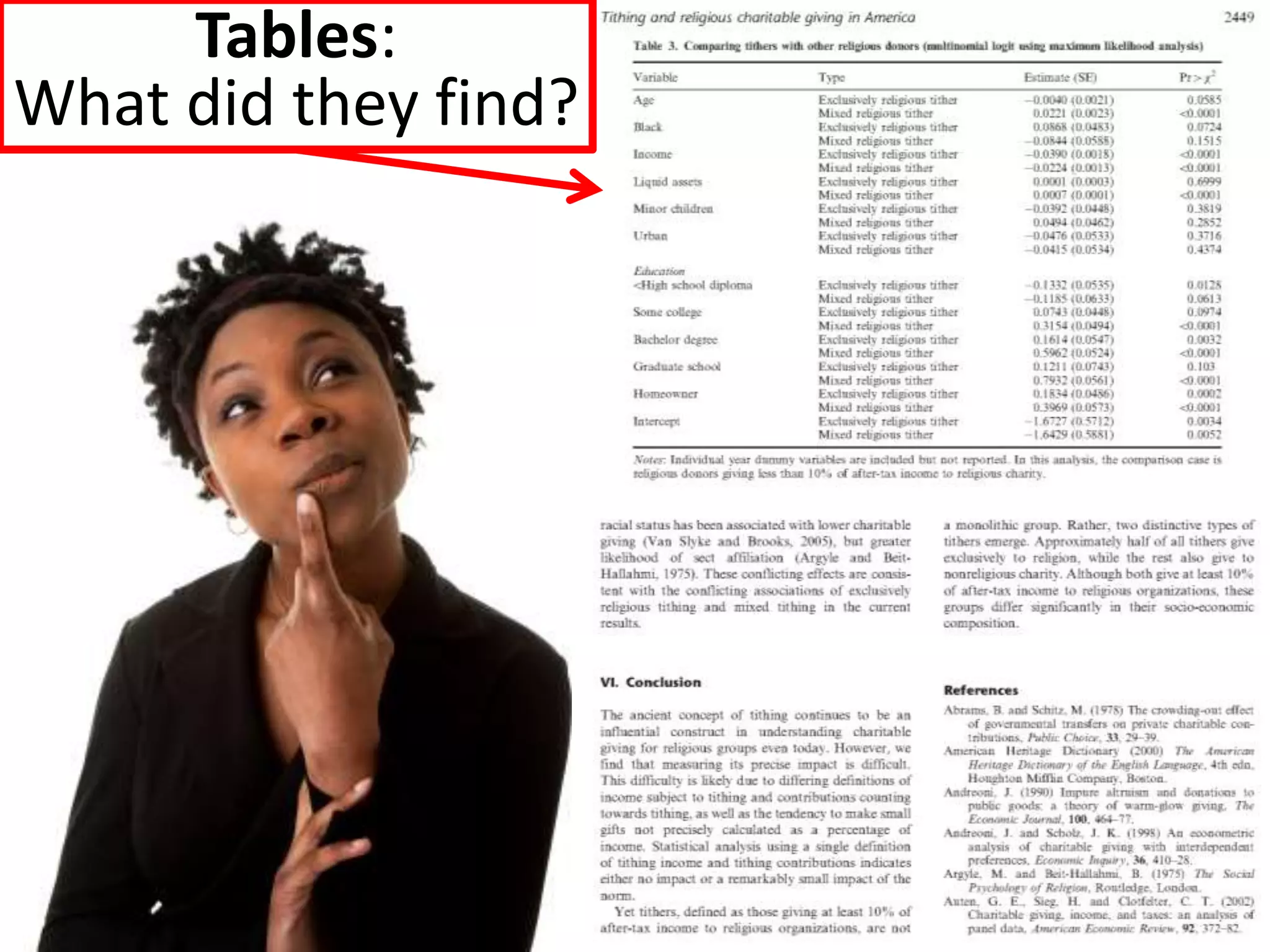
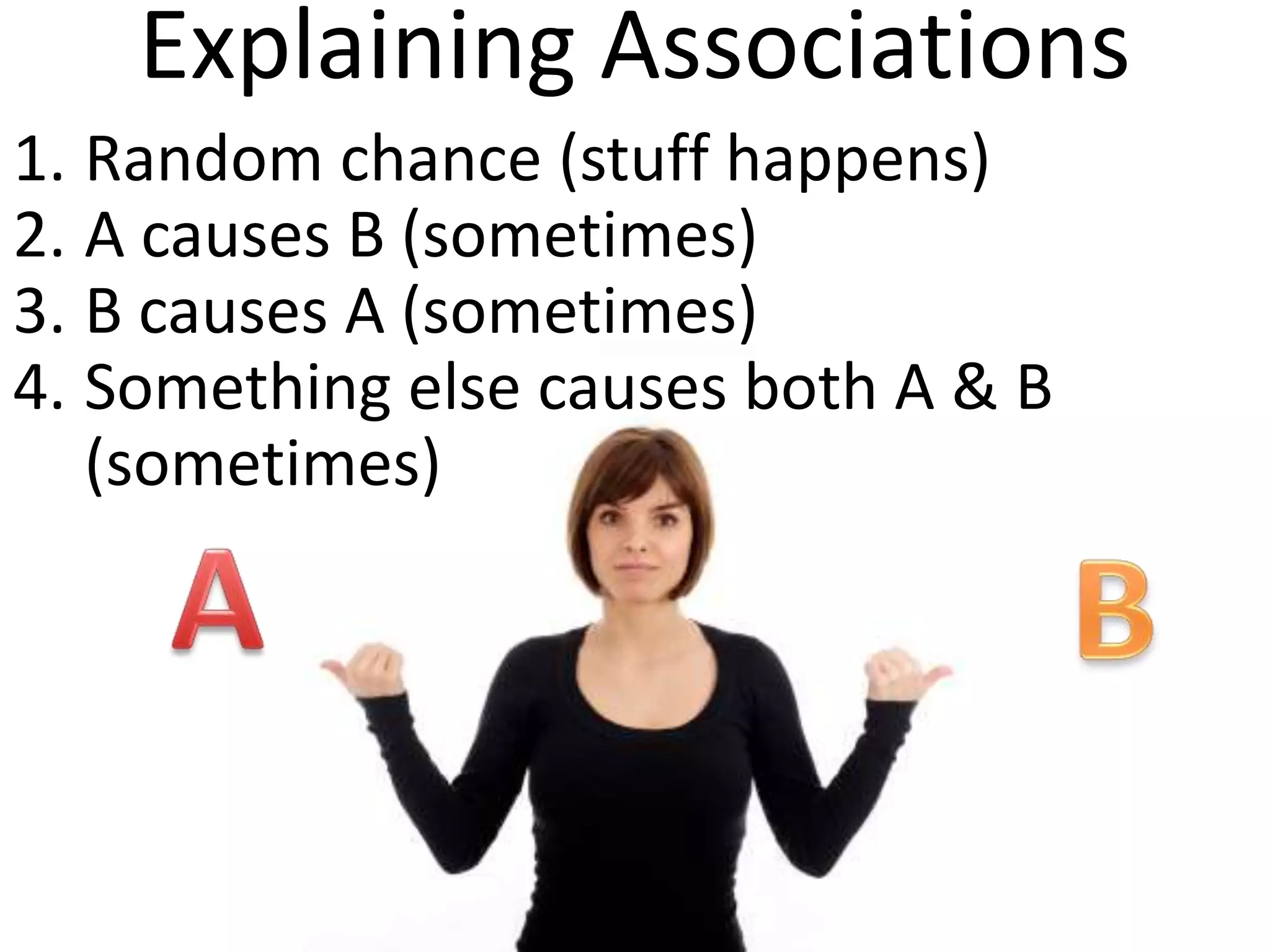
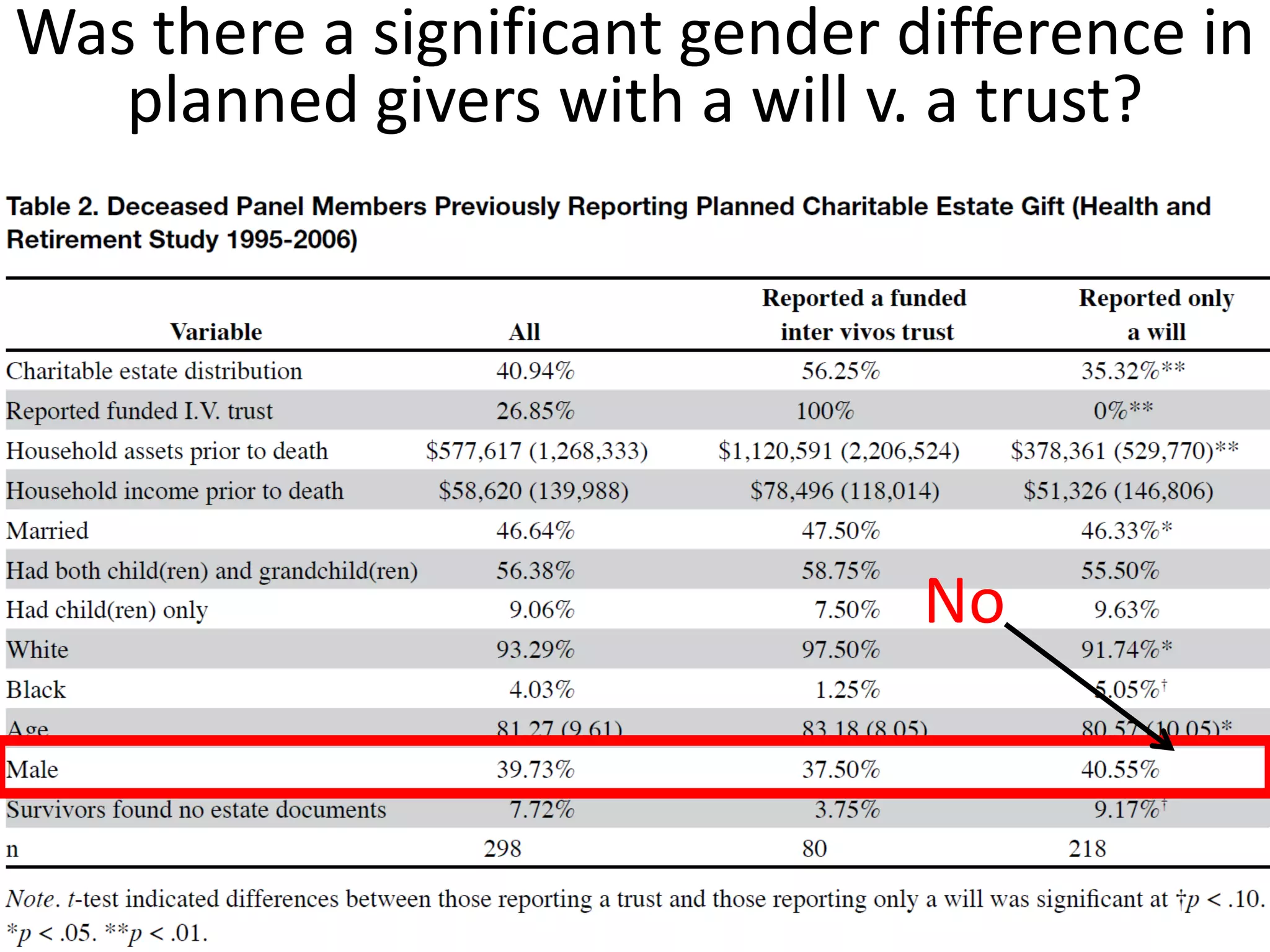
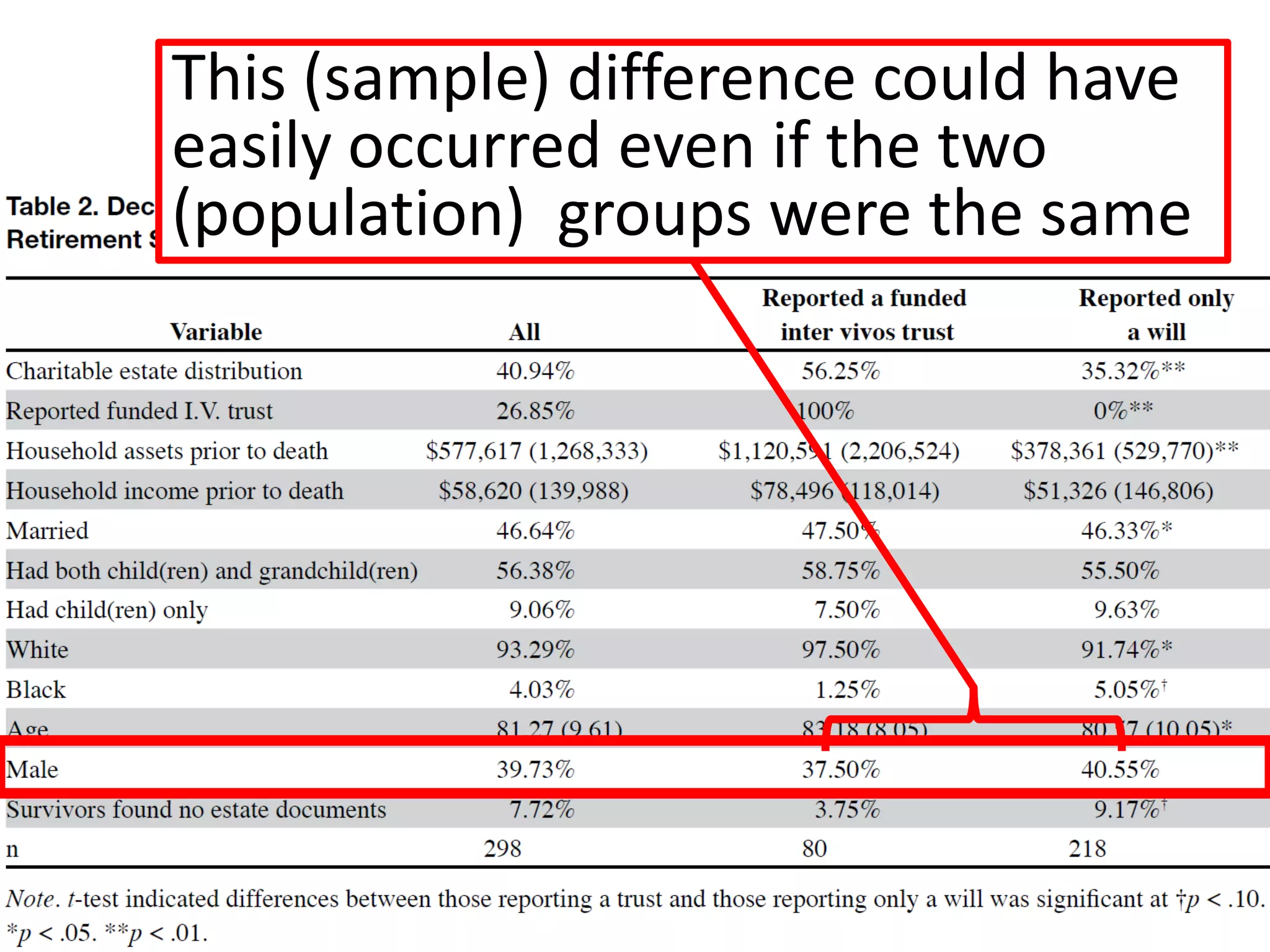
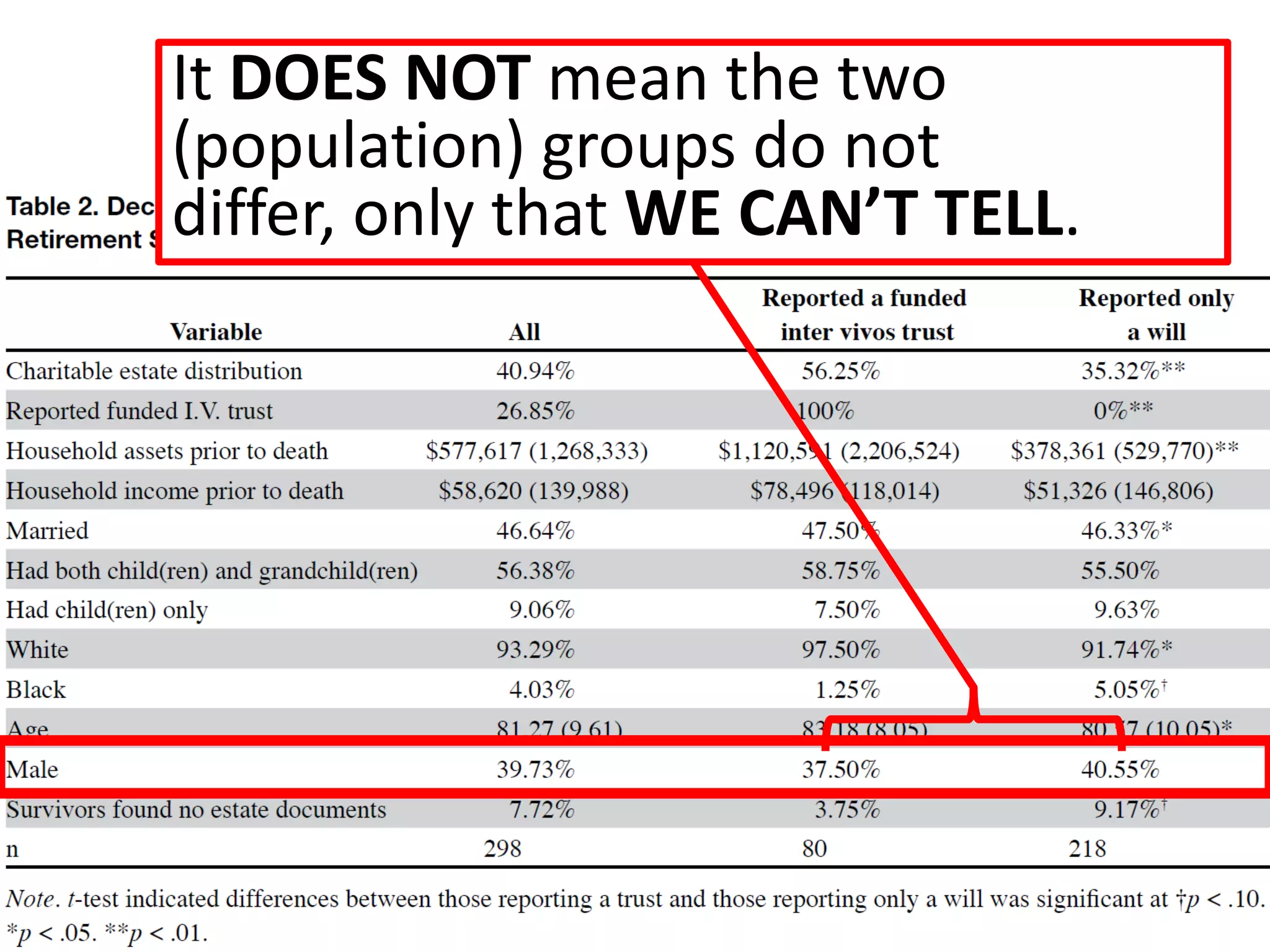
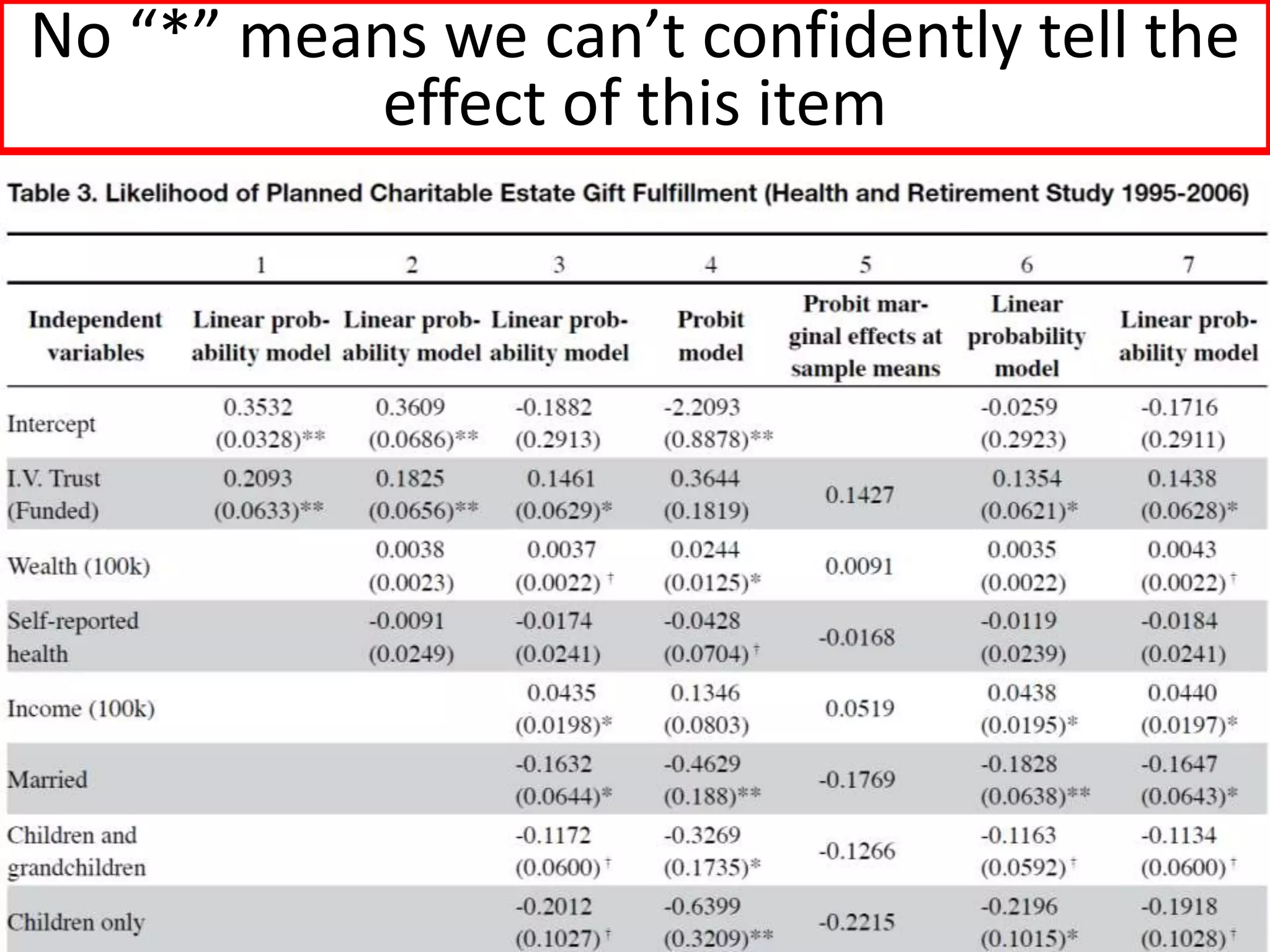
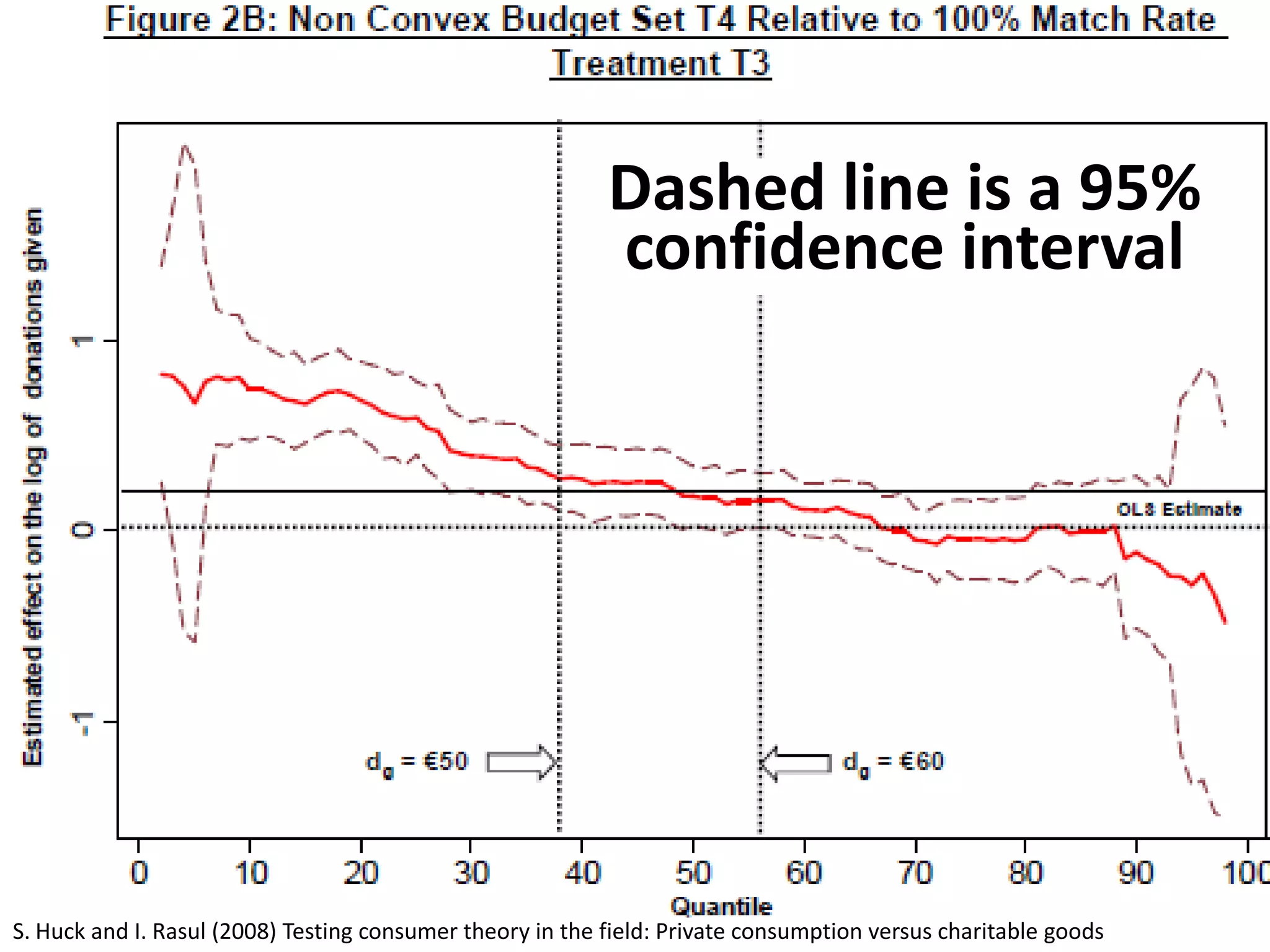
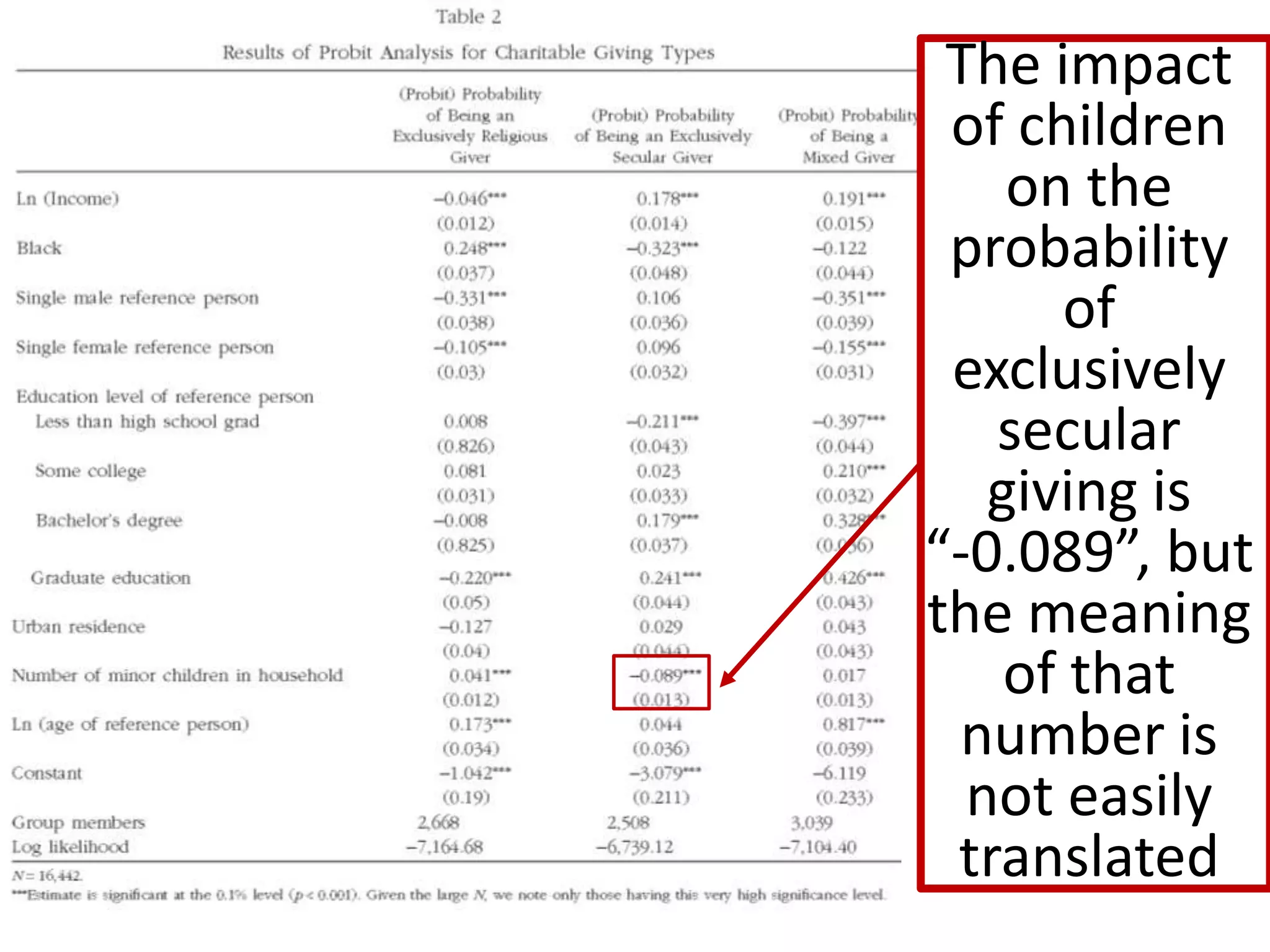
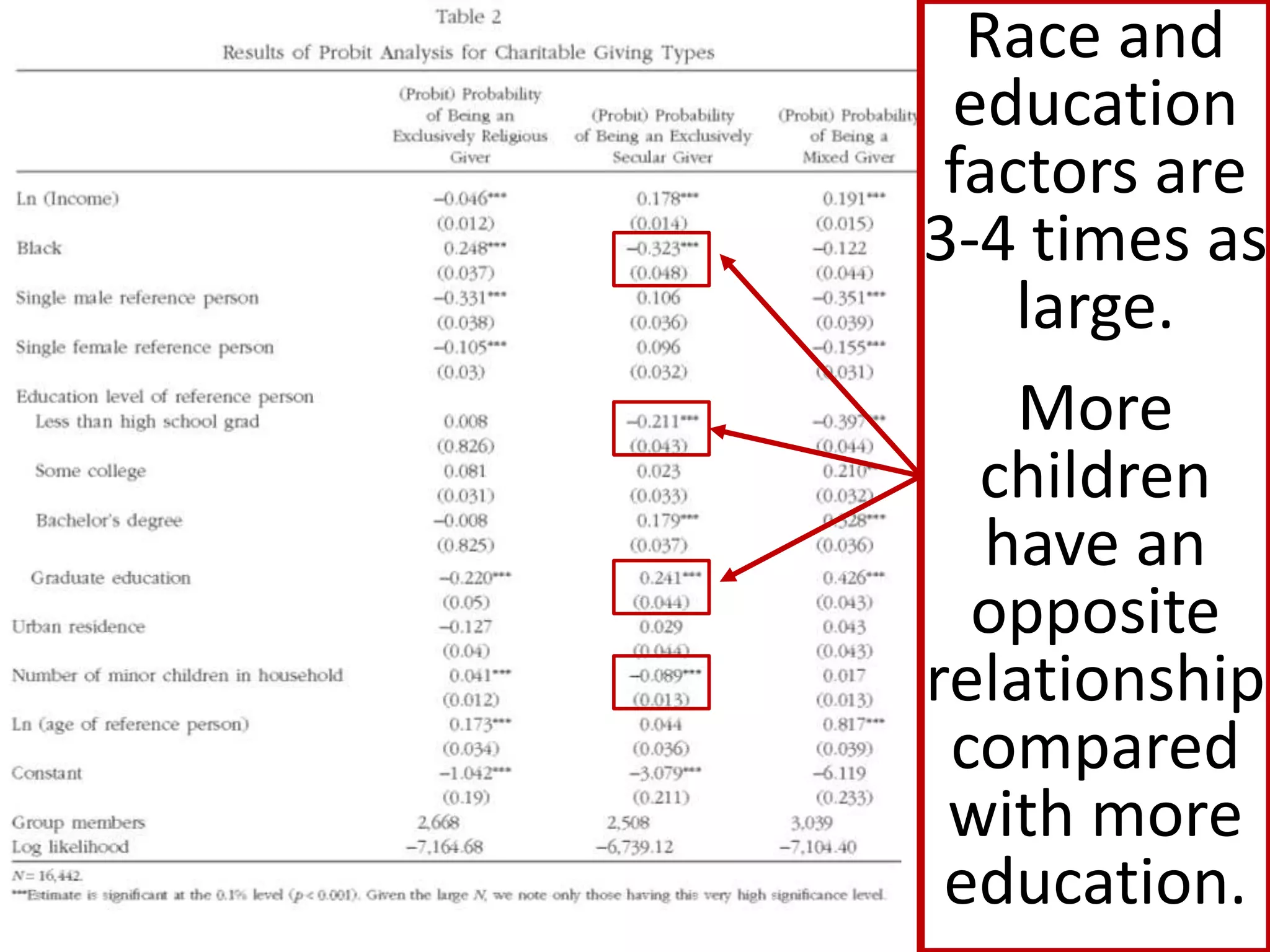
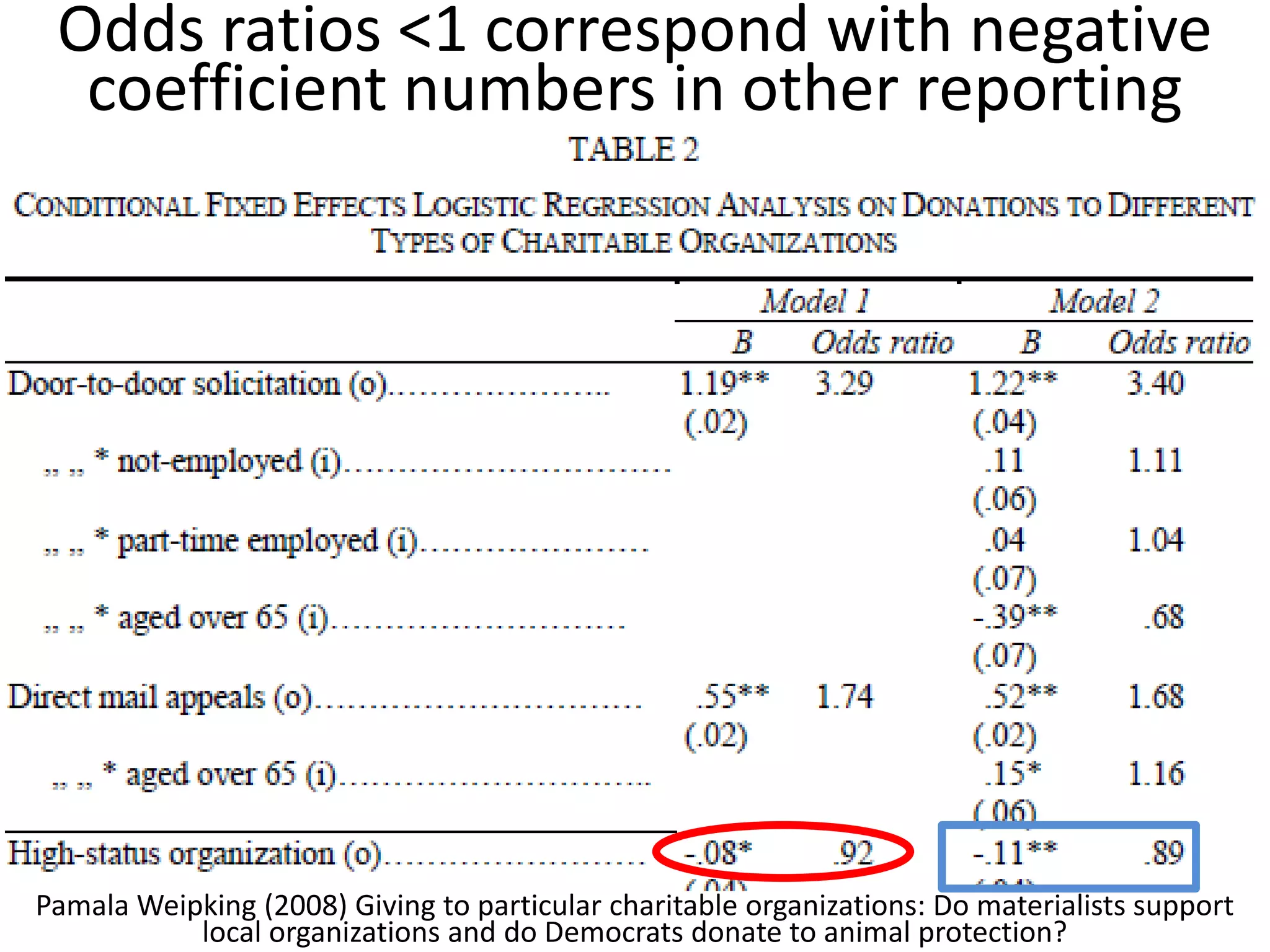
The document offers guidance on reading academic research effectively, especially for non-experts, emphasizing that one can extract key concepts without understanding every detail. It discusses statistical concepts such as association versus causation, significance versus magnitude, and correlation versus multiple regression, highlighting the importance of critical assessment of research findings. Additionally, it stresses the messy nature of research and the need for careful evaluation of results to distinguish strong findings from weak ones.

1. How to
read
academic
research
(even if you’re not an expert)
Dr. Russell James III, Texas Tech University
www.EncourageGenerosity.com

2. Rule 1
Don’t Freak
Out!

3. You don’t need to eat
the whole cow!
You can get
important
concepts out
of a research
article
without fully
understanding
every detail

4. How do you eat a
cake with rocks in it?
Don’t try to
eat the rocks

5. Questions for an article
1.Do I care about
the research
topic?
2.Do I believe the
findings?
3.So what?

6. Abstract: Do I care?
Tables: What did they really find?
Methods: Do I believe the table?
Discussion: So what?
Lit. Review: What did we already know?

7. Title and Abstract:
Do I care?

8. Tables:
What did they find?

9. Methods:
Should I believe
the table?

10. Discussion:
So What?

11. Literature Review:
What did we
already know?

12. Should you believe the findings?
Research is messy.
Research often disagrees.
We want to be able to
distinguish strong results
from weak ones.

13. Bad news
Knowing whether
you should believe
the findings
usually requires
some statistics

14. Core statistics concepts you must know
1. Association v. Causation
2. Correlation v. Multiple Regression
3. Significance v. Magnitude

15. Association v. Causation
Association: A & B tend to occur together
more frequently than one would expect by
random chance

16. Explaining Associations
1. Random chance (stuff happens)
2. A causes B (sometimes)
3. B causes A (sometimes)
4. Something else causes both A & B
(sometimes)

17. Sleeping in your shoes is associated
with waking up with a headache.
Why?

18. 1. Random chance
2. Sleeping in shoes causes headaches
3. The very early stages of a forthcoming
headache causes sleeping in shoes
4. Going to bed drunk causes both results

19. Association v. Causation
• Statistics can show
only association
• Statistics can NEVER
show causation
We infer causation from
experimental design or
theory combined with
statistical association

20. Statistics
can easily
determine
this
Explaining associations:
1. Random chance
2. A causes B
less so with
3. B causes A
these
4. Something else causes both A & B

21. Correlation
v.
Multiple
Regression

22. Correlation: A & B tend to occur
together more frequently than one
would expect by random chance
Multiple Regression: Above is true
when comparing those otherwise
similar in certain ways

23. Correlation
Higher education
and charitable giving
tend to occur
together (more
frequently than one
would expect by
random chance)

24. Multiple Regression
Higher education
and charitable giving
tend to occur
together (more
frequently than one
would expect by
random chance)
comparing those
with otherwise
similar income
and wealth

25. Explaining Associations:
1. Random chance
2. A causes B
3. B causes A
4. Something else
causes both A & B
Multiple regression
allows us to exclude
specific items from
#4, unless we can’t or
didn’t measure it.

26. Nature says kids’ nightlights cause myopia
“Although it does not
establish a causal link, the
statistical strength of the
association of night-time
light exposure and
childhood myopia does
suggest that the absence
of a daily period of
darkness during early
childhood is a potential
precipitating factor in the
development of myopia.”
G.E. Quinn, C.H. Shin, M. Maquire, R. Stone (University of Pennsylvania Medical School), 1999,
Myopia and Ambient Lighting at Night, Nature, 399, 113.

27. Nature says kids’ nightlights cause myopia
1. Random chance
2. A causes B
3. B causes A
4. Something else
causes both A & B
G.E. Quinn, C.H. Shin, M. Maquire, R. Stone (University of Pennsylvania Medical School), 1999,
Myopia and Ambient Lighting at Night, Nature, 399, 113.

28. Rebuttal: Maybe parents’ myopia causes
both nightlights and child’s myopia?
“…we find that myopic
parents are more likely to
employ night-time lighting
aids for their children.
Moreover, there is an
association between myopia
in parents and their
children…”
“…Quinn et al.’s study should
have controlled for parental
myopia.”
J. Gwiazda, E. Ong, R. Held, F. Thorn (New England College of Optometry), 2000, Myopia and
Ambient Night-Time Lighting, Nature, 399, 113.

29. Significance
v.
Magnitude

30. Statistics tests a small sample to
predict the whole population
Significance shows how likely
our result might have been
due to an unusual random
sample, rather than an actual
difference in the population

31. Most papers report some measure of statistical
significance (chance that the association was
due to a weird random sample)
• p-value
• confidence interval

32. How likely is it to randomly draw
these five fruits from a truckload
with as many apples as oranges?
p-value

33. p-value
p<.05 = there is less than a 5% chance that
the result was caused by an unusual
random sample where there was
no actual (population) difference

34. Was there a significant gender difference in
planned givers with a will v. a trust?
No

36. This (sample) difference could have
easily occurred even if the two
(population) groups were the same

37. It DOES NOT mean the two
(population) groups do not differ,
only that WE CAN’T TELL.

38. No “*” means we can’t confidently tell the
effect of this item

39. 95% Confidence interval
If you kept taking random samples, 95%
of the time the true (population) value
would appear inside the confidence
interval associated with each sample
Sample
Average
Strength Population
Average
Strength
Confidence Interval

40. Dashed line is a 95%
confidence interval
S. Huck and I. Rasul (2008) Testing consumer theory in the field: Private consumption versus charitable goods

41. Multiple Comparisons Problem
How likely is it to randomly draw
these five fruits from a truckload
with as many apples as oranges?
Would your answer change if I got
to draw 20 times to find this group?

42. If all variables are random, about one
out of 20 will have a p-value<.05

43. “We tested 100 items and found 5
to be significant at p<.05.”

44. Significance v. Magnitude
It is possible to be highly confident of a
very small effect. This may be publishable,
but not practically important.

45. Numbers
(coefficients) resulting
from complex
statistical techniques
may not be directly
interpretable in terms
of real world
magnitude

46. The impact
of children
on the
probability
of
exclusively
secular
giving is
“-0.089”, but
the meaning
of that
number is
not easily
translated

47. Even with complex techniques, we
can easily compare sign and
magnitude relative to other variables

48. Race and
education
factors are
3-4 times as
large.
More
children
have an
opposite
relationship
compared
with more
education.

49. Odds ratios are different
Usually you can
compare sign and
size, but odds ratios
are always positive

50. Odds ratios: the odds of an event occurring
in one group over the odds of it occurring
in another group
<1 negative; >1 positive; =1 none

51. Odds ratios <1 correspond with negative
coefficient numbers in other reporting
Pamala Weipking (2008) Giving to particular charitable organizations: Do materialists support
local organizations and do Democrats donate to animal protection?

52. Finding academic research articles
ISI ranked academic
Includes everything, journals articles only
even working
papers and
industry literature

53. How to
read
academic
research
(even if you’re not an expert)
Dr. Russell James III, Texas Tech University
www.EncourageGenerosity.com