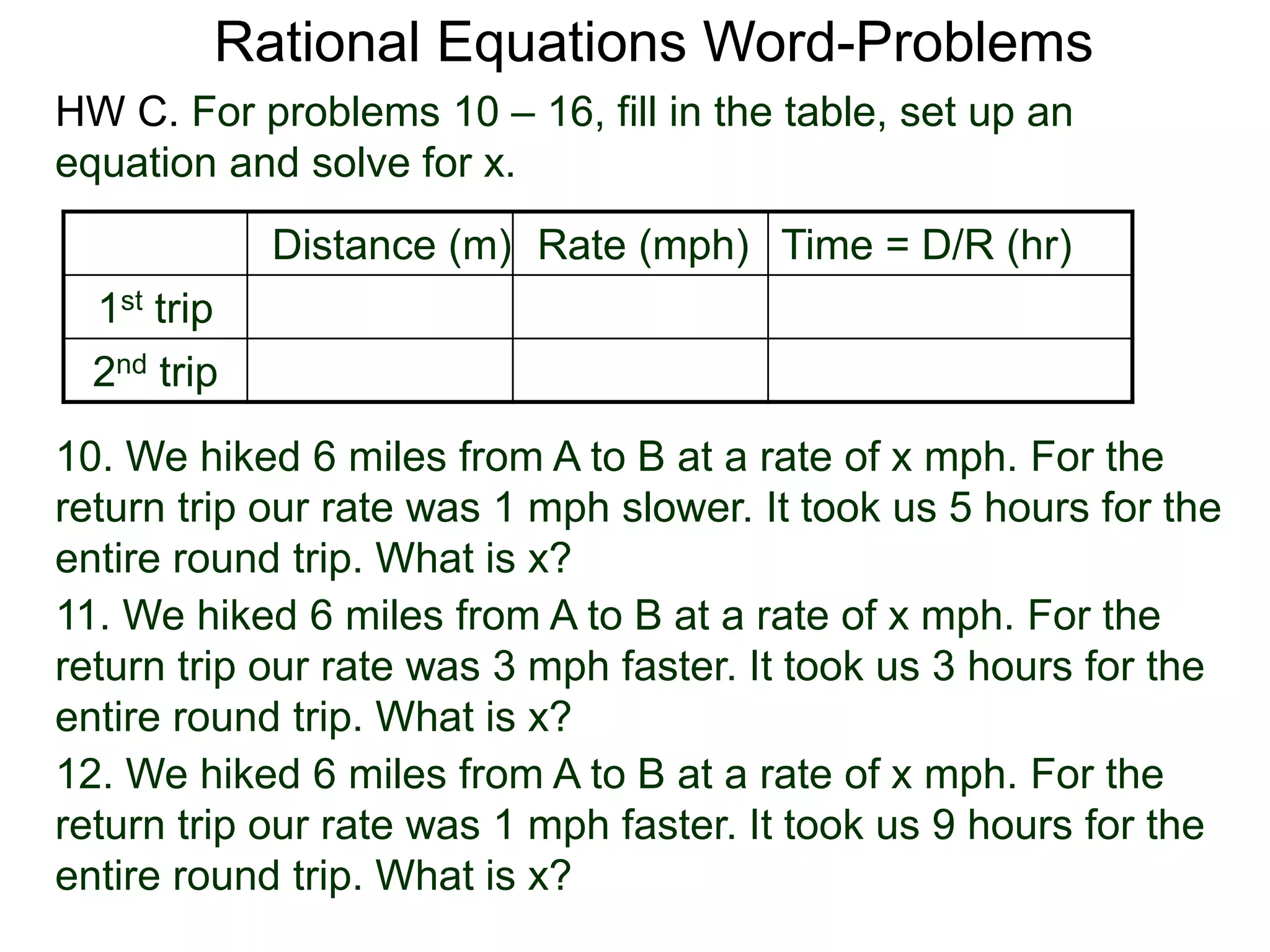
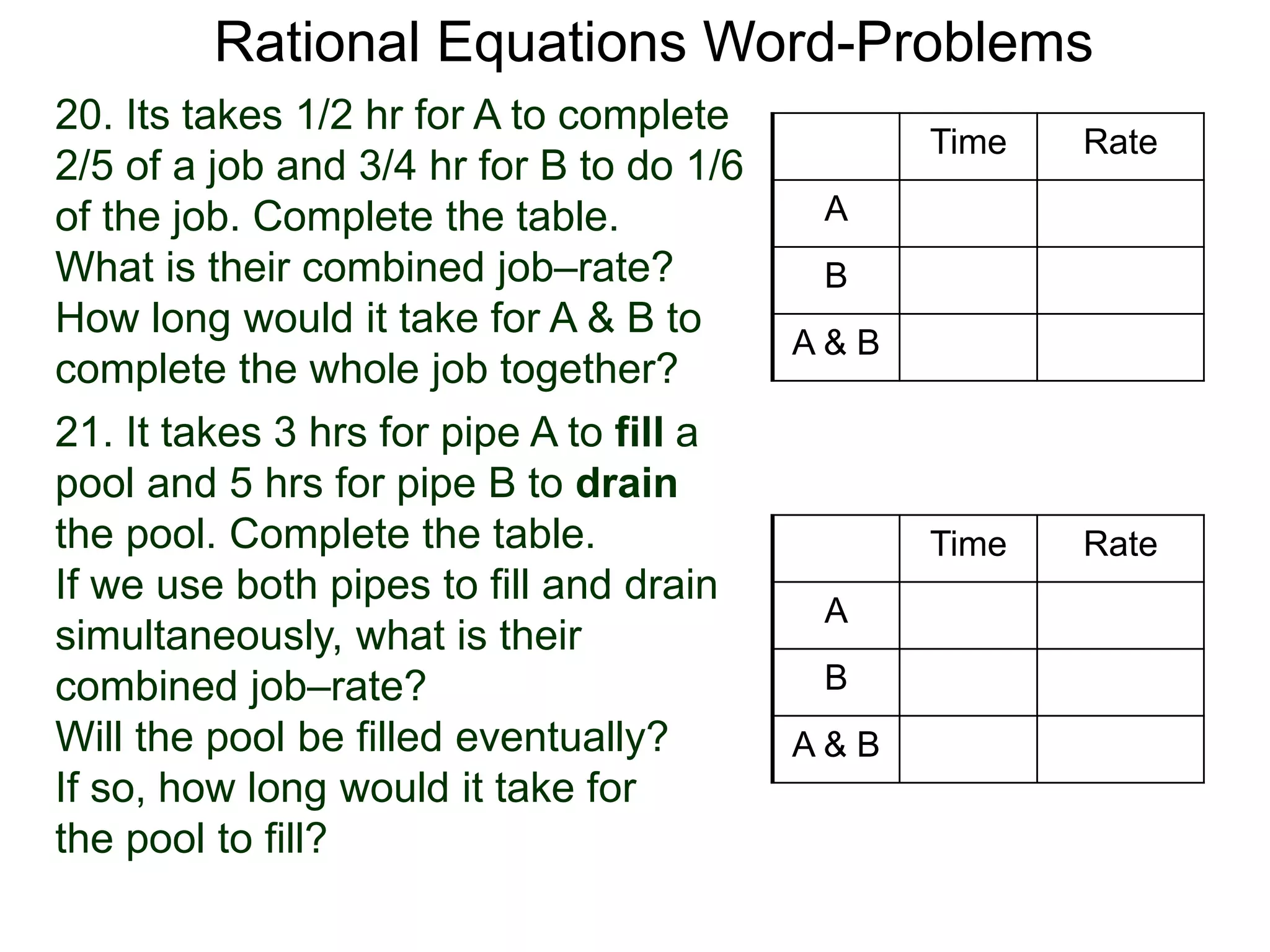
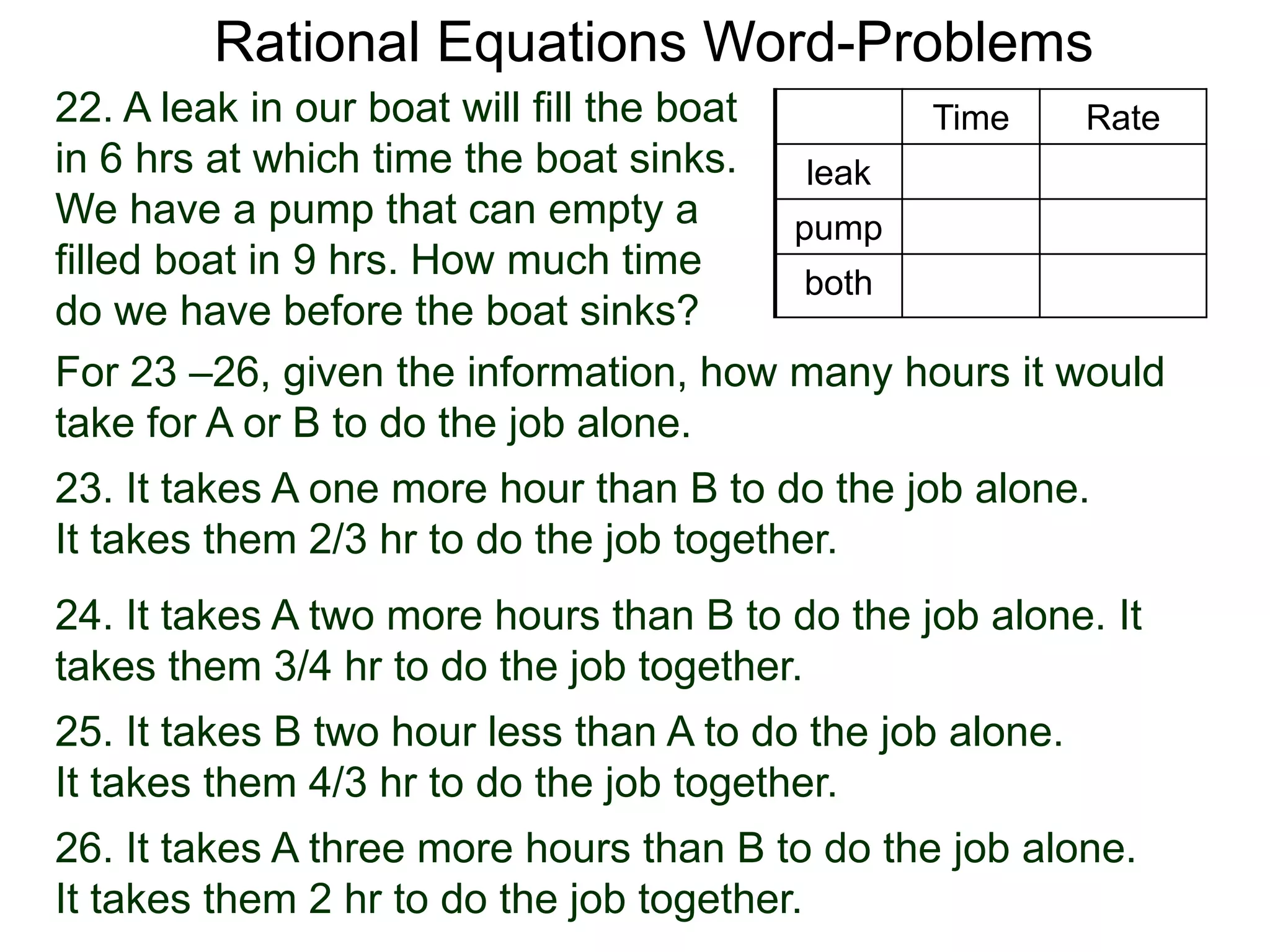
The document discusses using rational equations to solve word problems involving costs shared among groups of people. It provides an example where a taxi costs $20 to rent for a group of x people, with the cost shared equally. If one person leaves the group, the remaining people each pay $1 more. Setting up the cost equations and subtracting them allows determining that x must equal 5 people for the equations to hold true. A table is suggested to organize calculations for different inputs when solving similar rational equation word problems.
















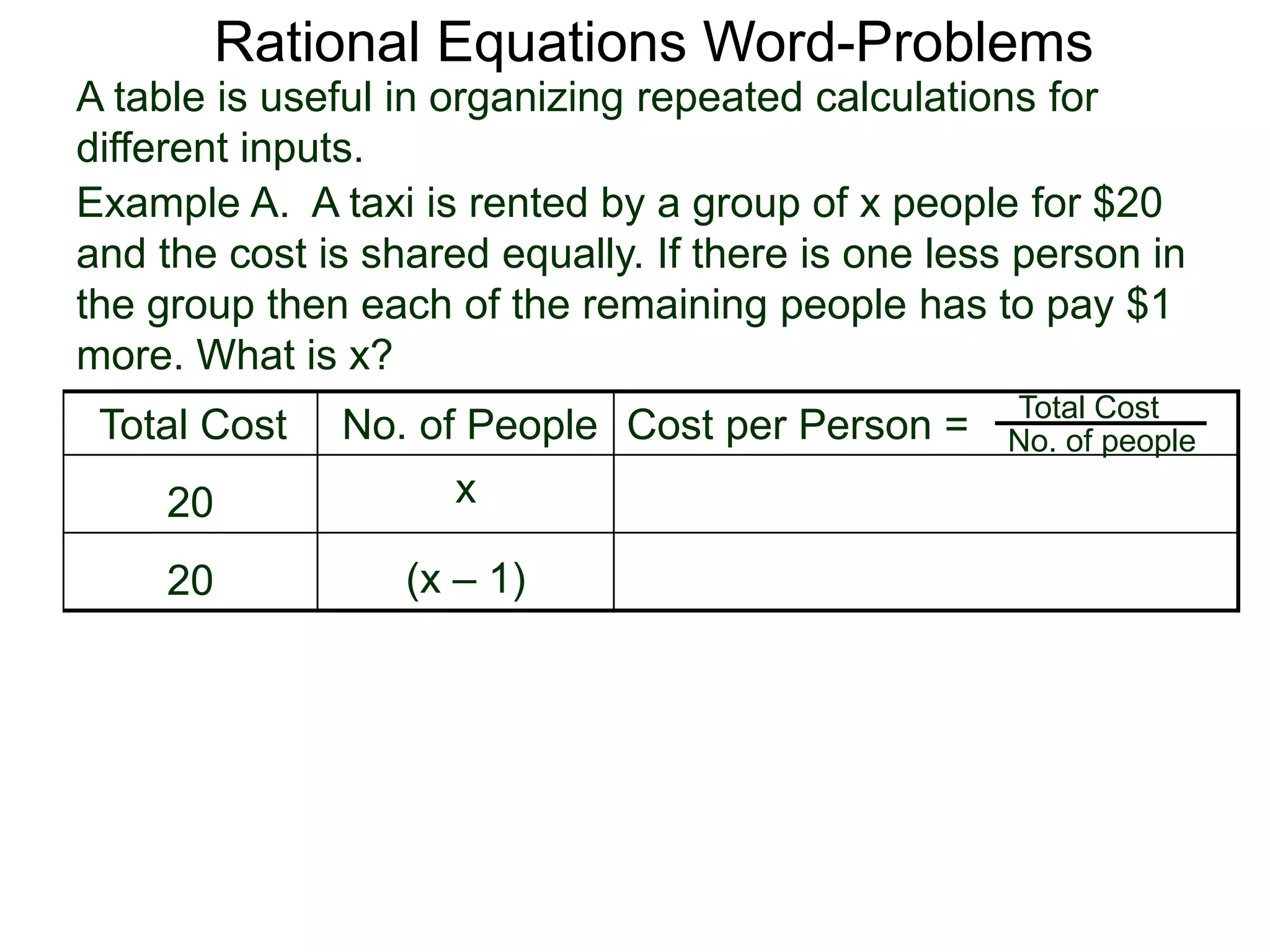





![Rational Equations Word-Problems
Example A. A taxi is rented by a group of x people for $20
and the cost is shared equally. If there is one less person in
the group then each of the remaining people has to pay $1
more. What is x?
Total Cost No. of People Cost per Person =
20 x
20 (x – 1)
Total Cost
No. of people
20
x
20
(x – 1)
20
(x – 1)
Let’s compare the two different per/person costs.
– = 1[ ] x (x – 1) clear the denominators
by LCM
A table is useful in organizing repeated calculations for
different inputs.
20
x](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-23-2048.jpg)
![Rational Equations Word-Problems
Example A. A taxi is rented by a group of x people for $20
and the cost is shared equally. If there is one less person in
the group then each of the remaining people has to pay $1
more. What is x?
Total Cost No. of People Cost per Person =
20 x
20 (x – 1)
Total Cost
No. of people
20
x
20
(x – 1)
20
(x – 1)
20
x
Let’s compare the two different per/person costs.
– = 1[ ] x (x – 1) clear the denominators
by LCM
x (x – 1) x (x – 1)
A table is useful in organizing repeated calculations for
different inputs.](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-24-2048.jpg)
![Rational Equations Word-Problems
Example A. A taxi is rented by a group of x people for $20
and the cost is shared equally. If there is one less person in
the group then each of the remaining people has to pay $1
more. What is x?
Total Cost No. of People Cost per Person =
20 x
20 (x – 1)
Total Cost
No. of people
20
x
20
(x – 1)
20
(x – 1)
Let’s compare the two different per/person costs.
= 1[ ] x (x – 1) clear the denominators
by LCM
x (x – 1) x (x – 1)
20x – 20(x – 1) = x(x – 1)
A table is useful in organizing repeated calculations for
different inputs.
20
x
–](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-25-2048.jpg)
![Rational Equations Word-Problems
Example A. A taxi is rented by a group of x people for $20
and the cost is shared equally. If there is one less person in
the group then each of the remaining people has to pay $1
more. What is x?
Total Cost No. of People Cost per Person =
20 x
20 (x – 1)
Total Cost
No. of people
20
x
20
(x – 1)
20
(x – 1)
Let’s compare the two different per/person costs.
= 1[ ] x (x – 1) clear the denominators
by LCM
x (x – 1) x (x – 1)
20x – 20(x – 1) = x(x – 1)
20x – 20x + 20 = x2 – x
A table is useful in organizing repeated calculations for
different inputs.
20
x
–](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-26-2048.jpg)
![Rational Equations Word-Problems
Example A. A taxi is rented by a group of x people for $20
and the cost is shared equally. If there is one less person in
the group then each of the remaining people has to pay $1
more. What is x?
Total Cost No. of People Cost per Person =
20 x
20 (x – 1)
Total Cost
No. of people
20
x
20
(x – 1)
20
(x – 1)
Let’s compare the two different per/person costs.
= 1[ ] x (x – 1) clear the denominators
by LCM
x (x – 1) x (x – 1)
20x – 20(x – 1) = x(x – 1)
A table is useful in organizing repeated calculations for
different inputs.
0 = x2 – x – 20
set one side as 0
20
x
–
20x – 20x + 20 = x2 – x](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-27-2048.jpg)















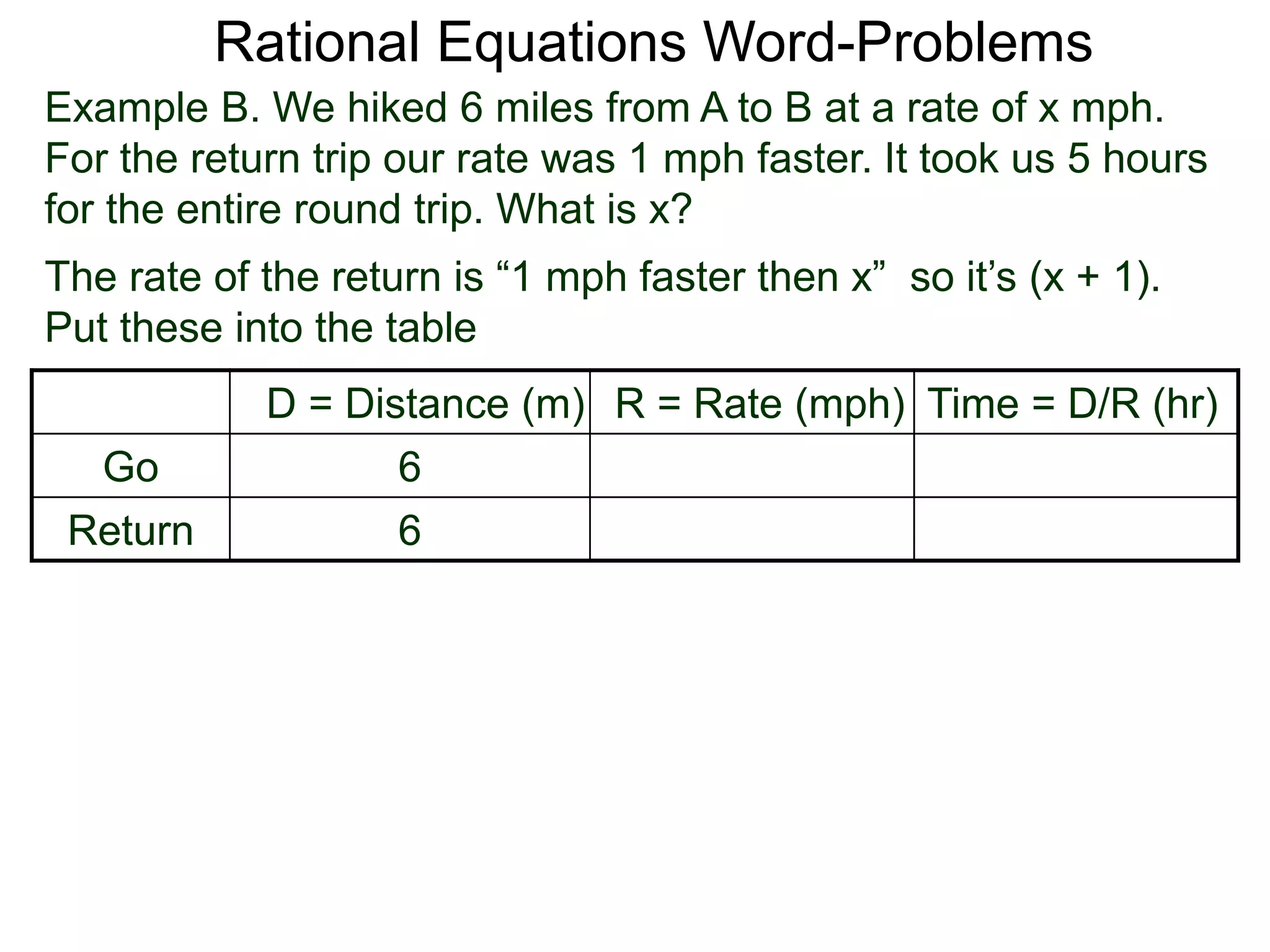
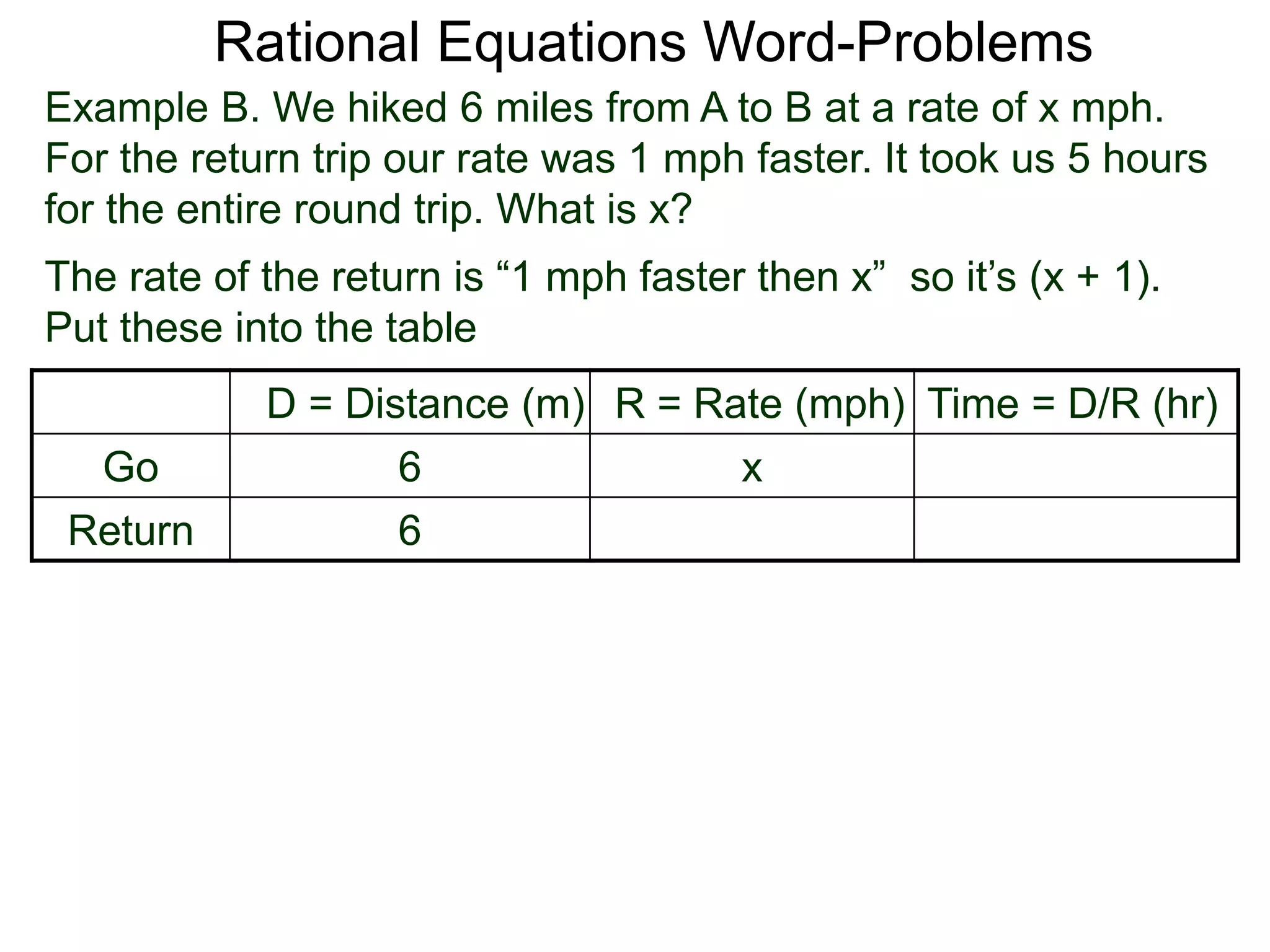
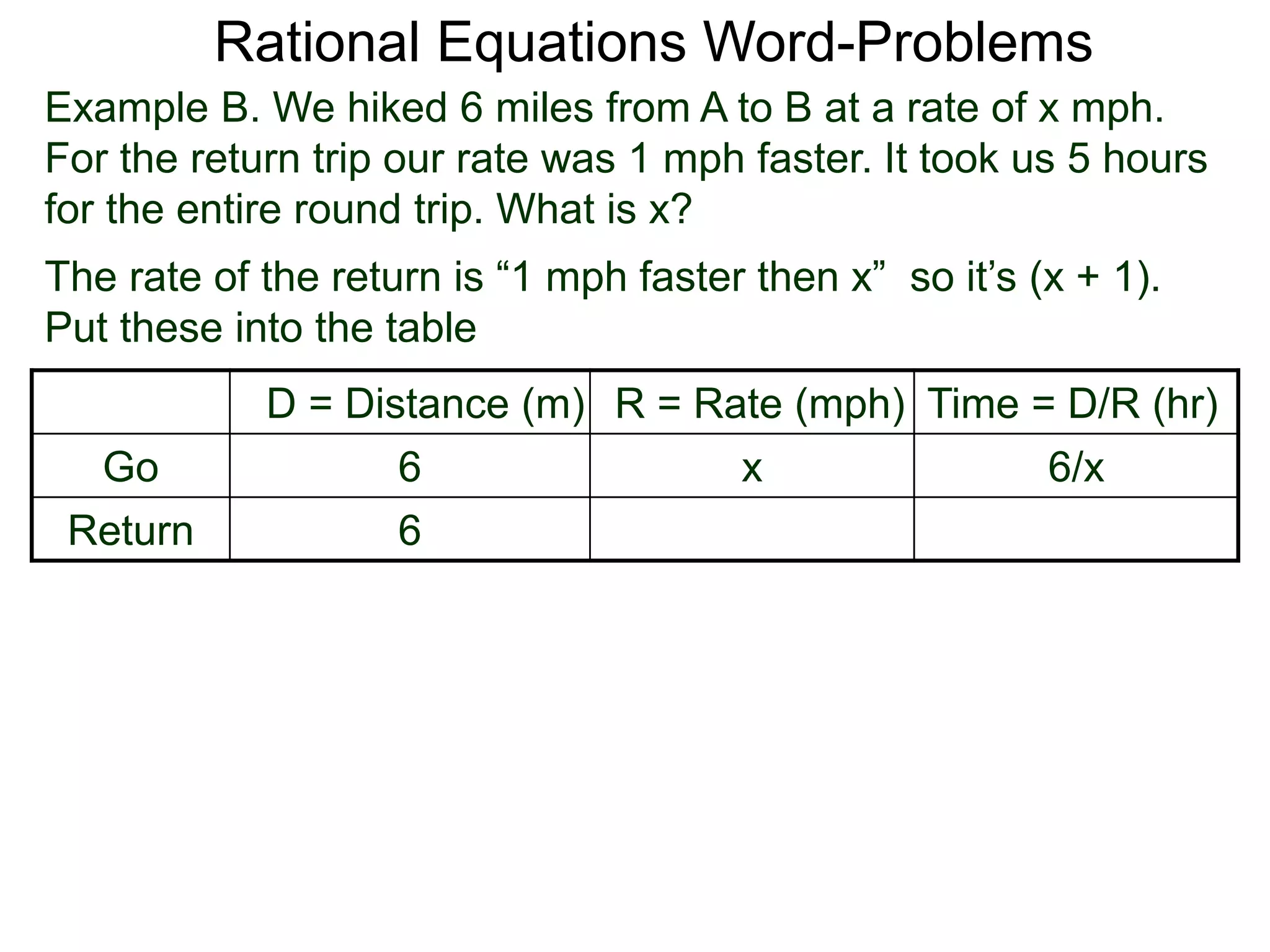
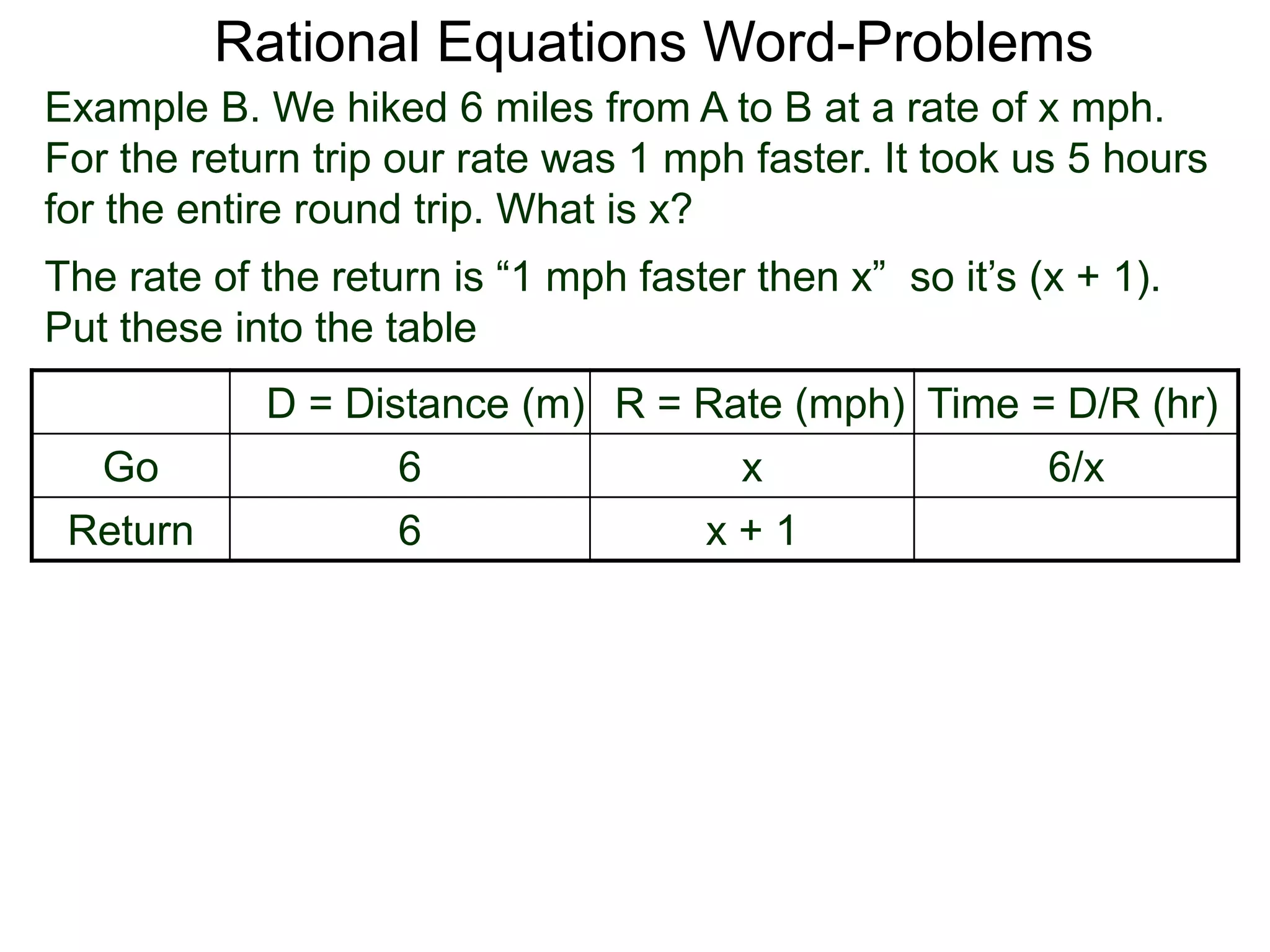
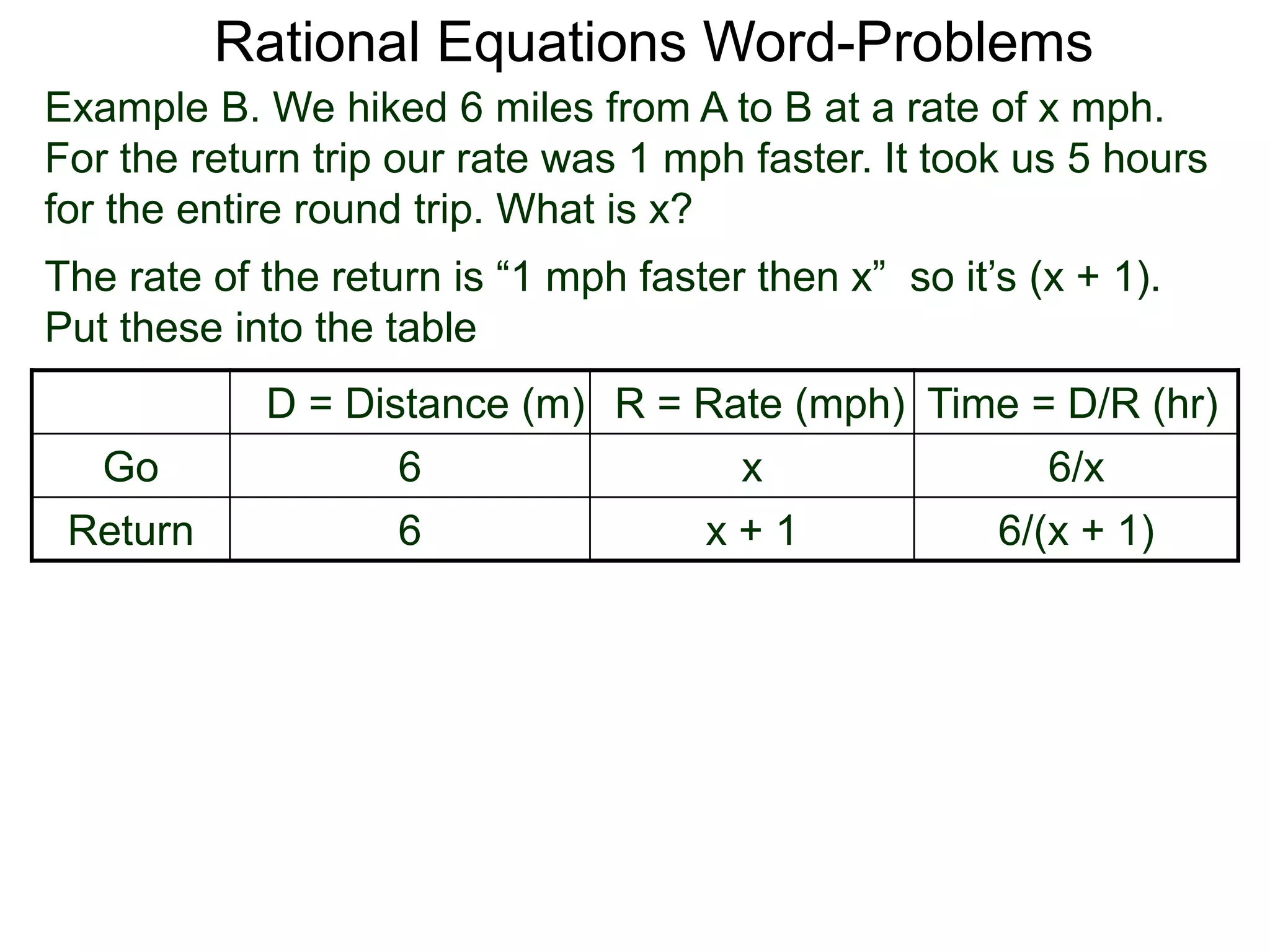

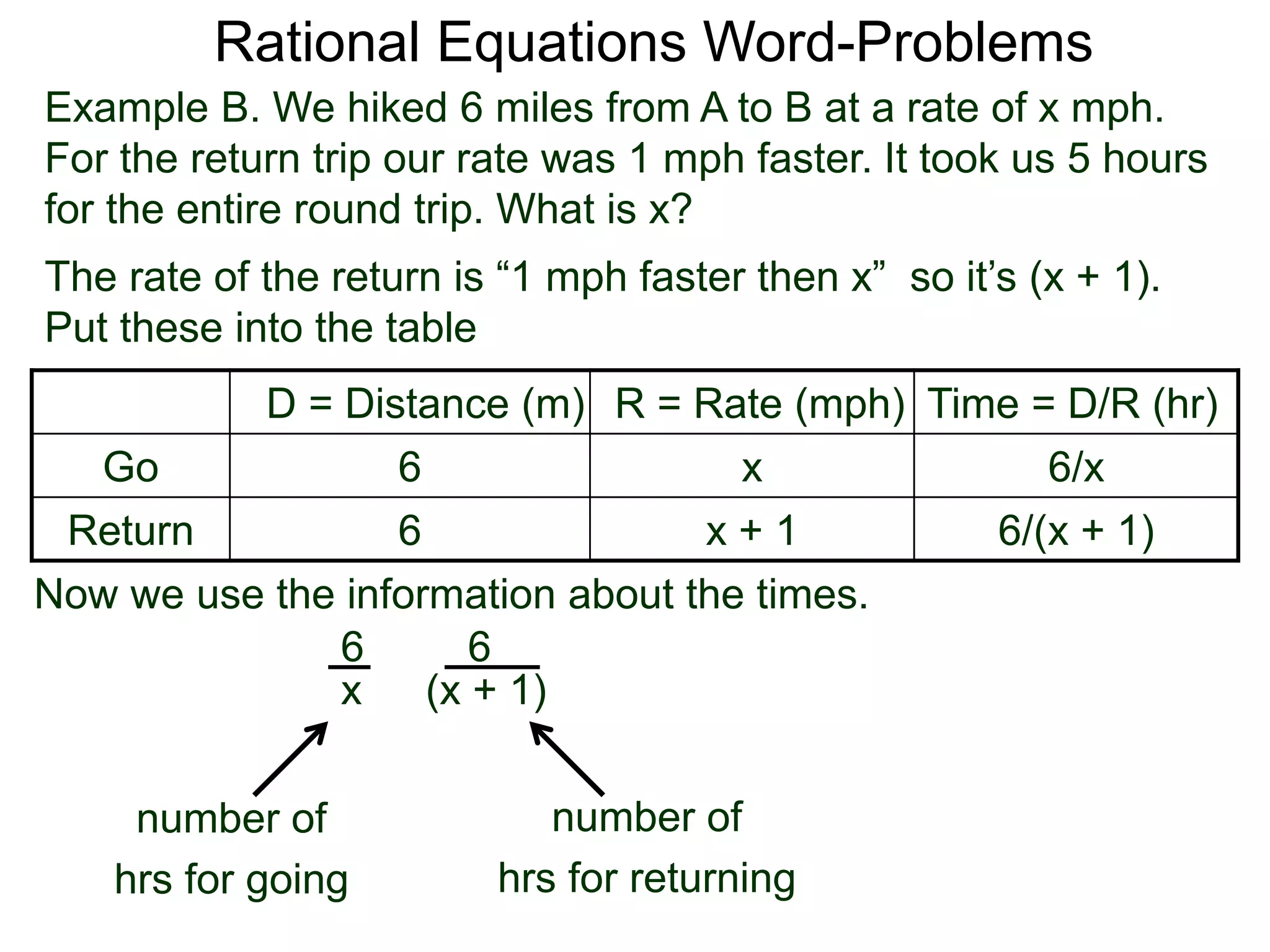

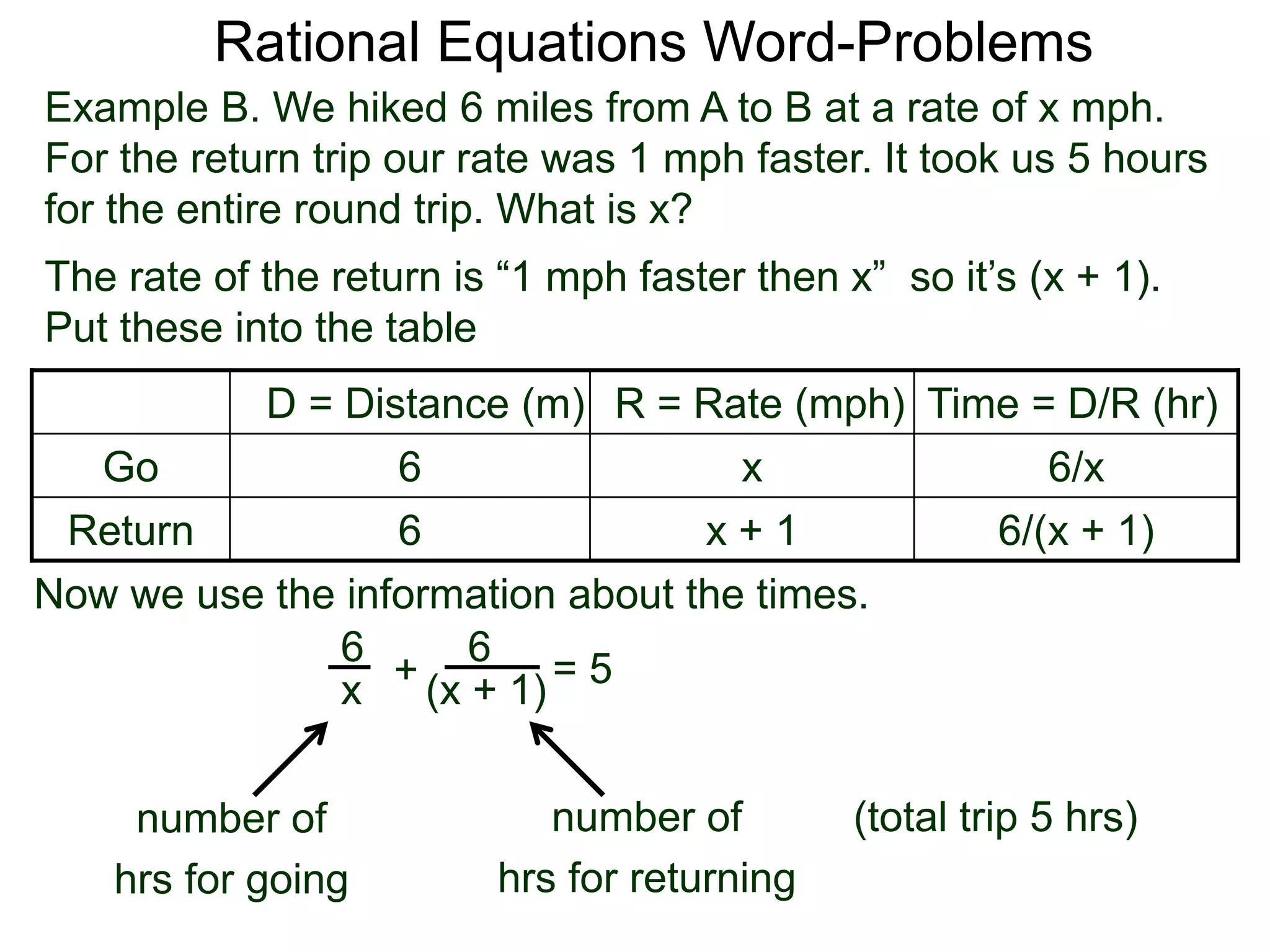





























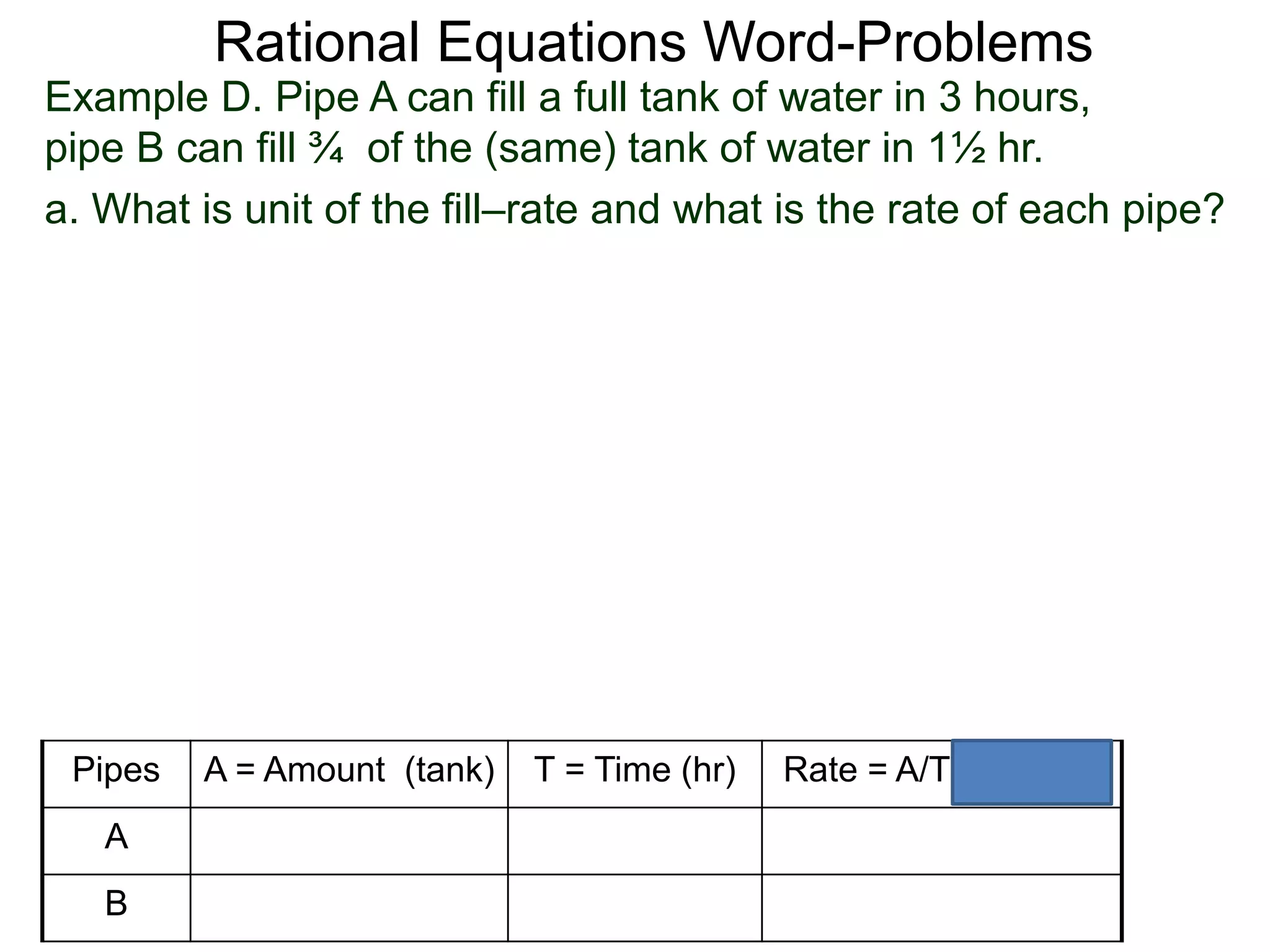
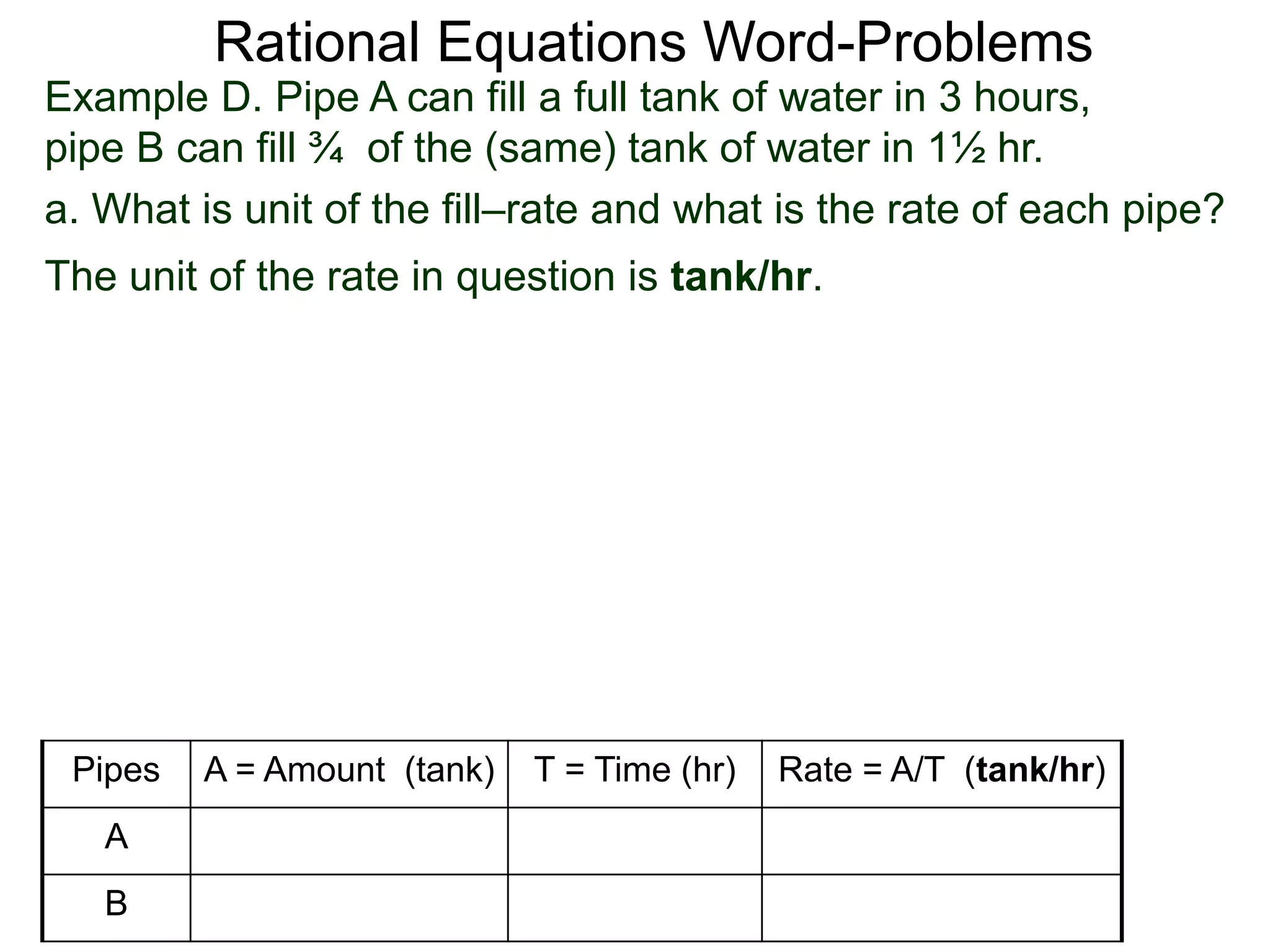
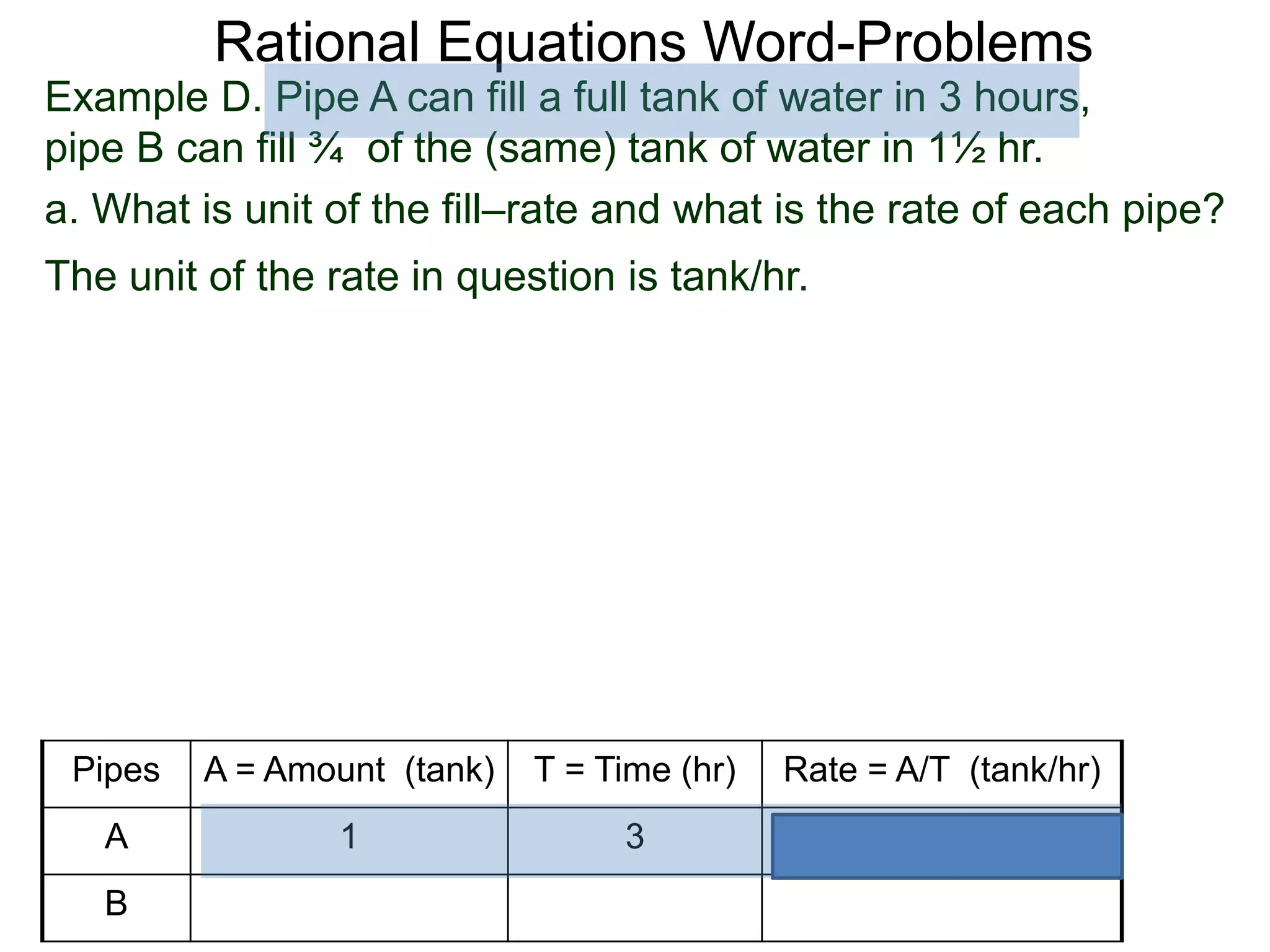
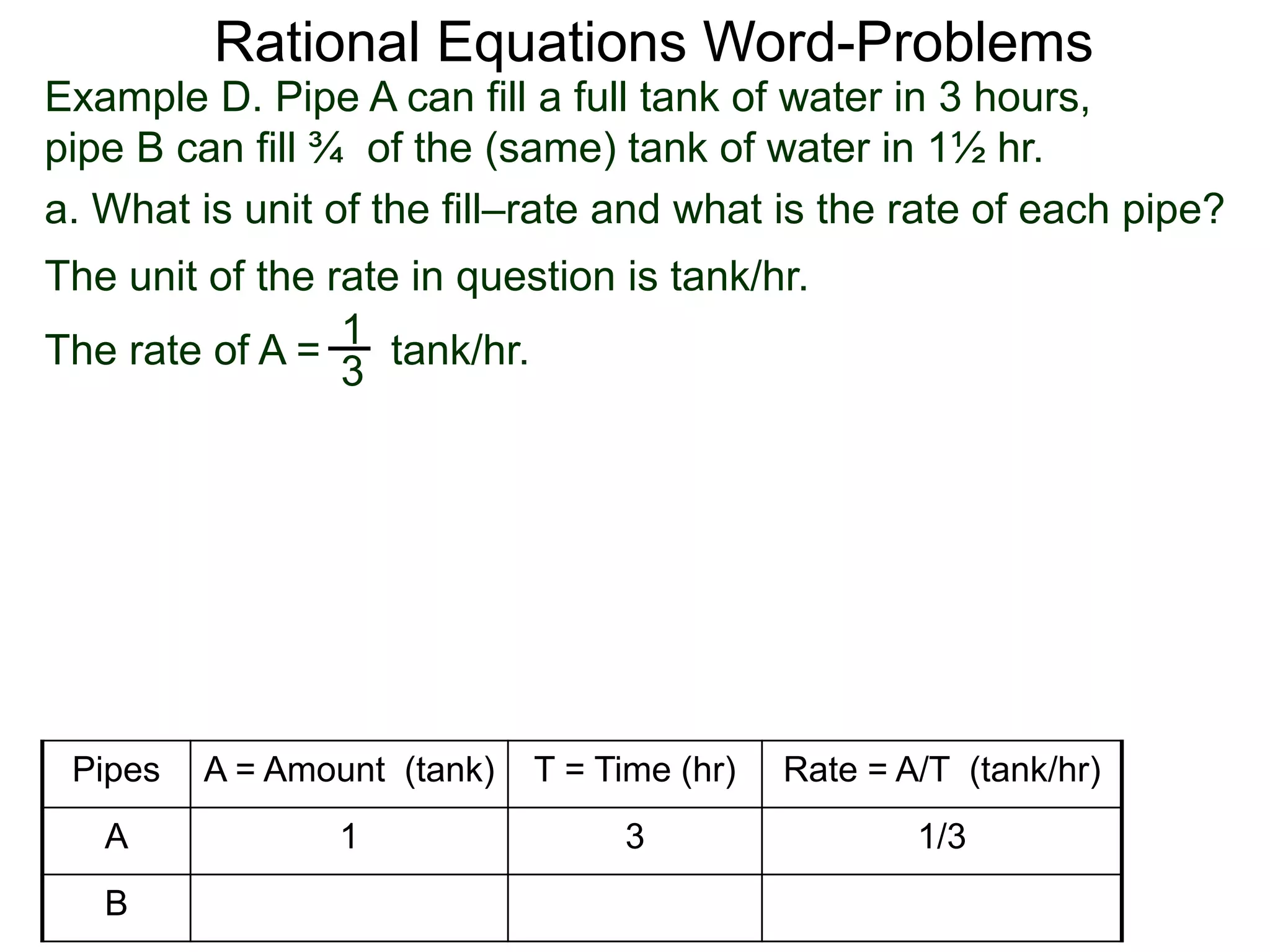



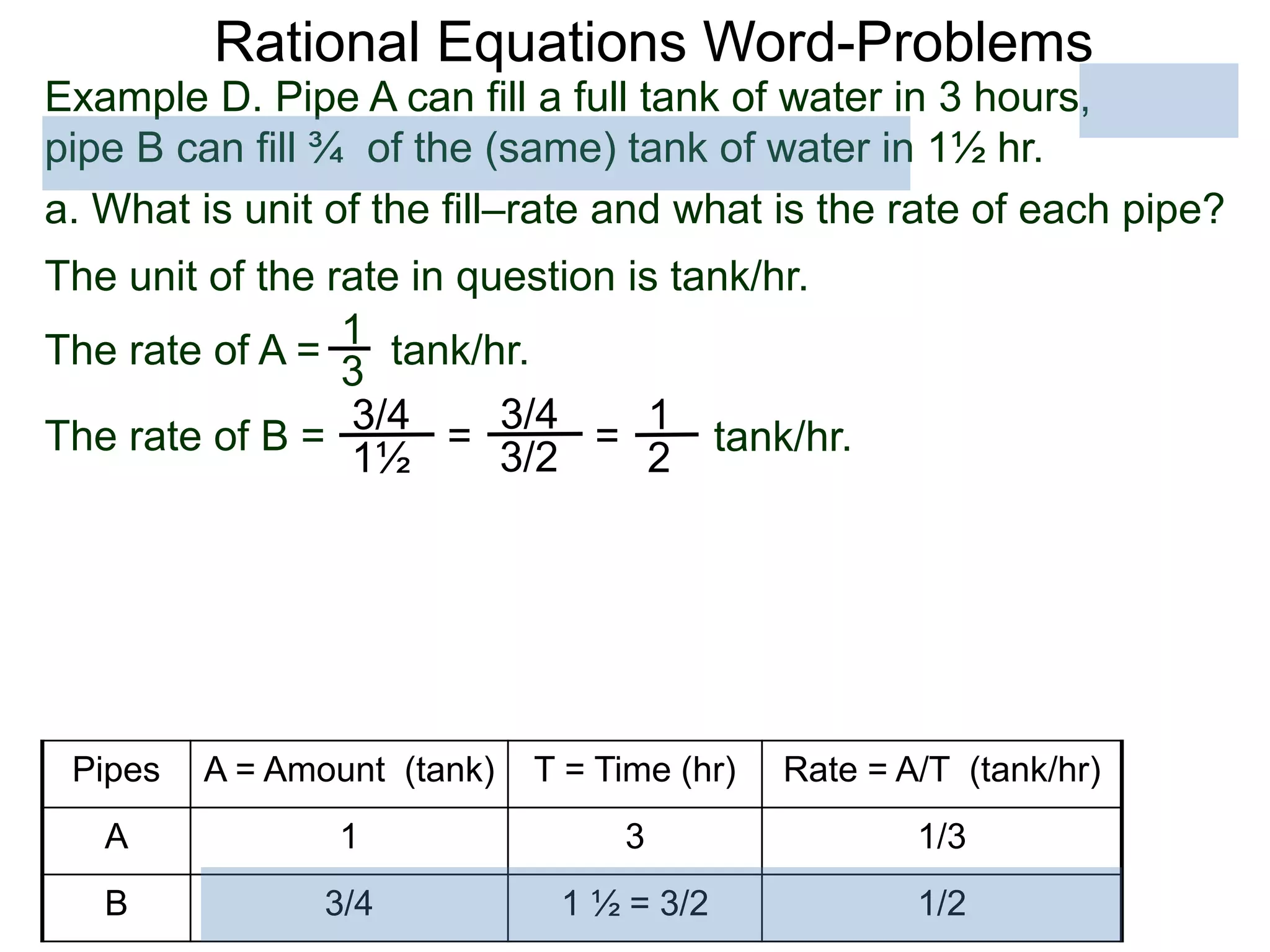
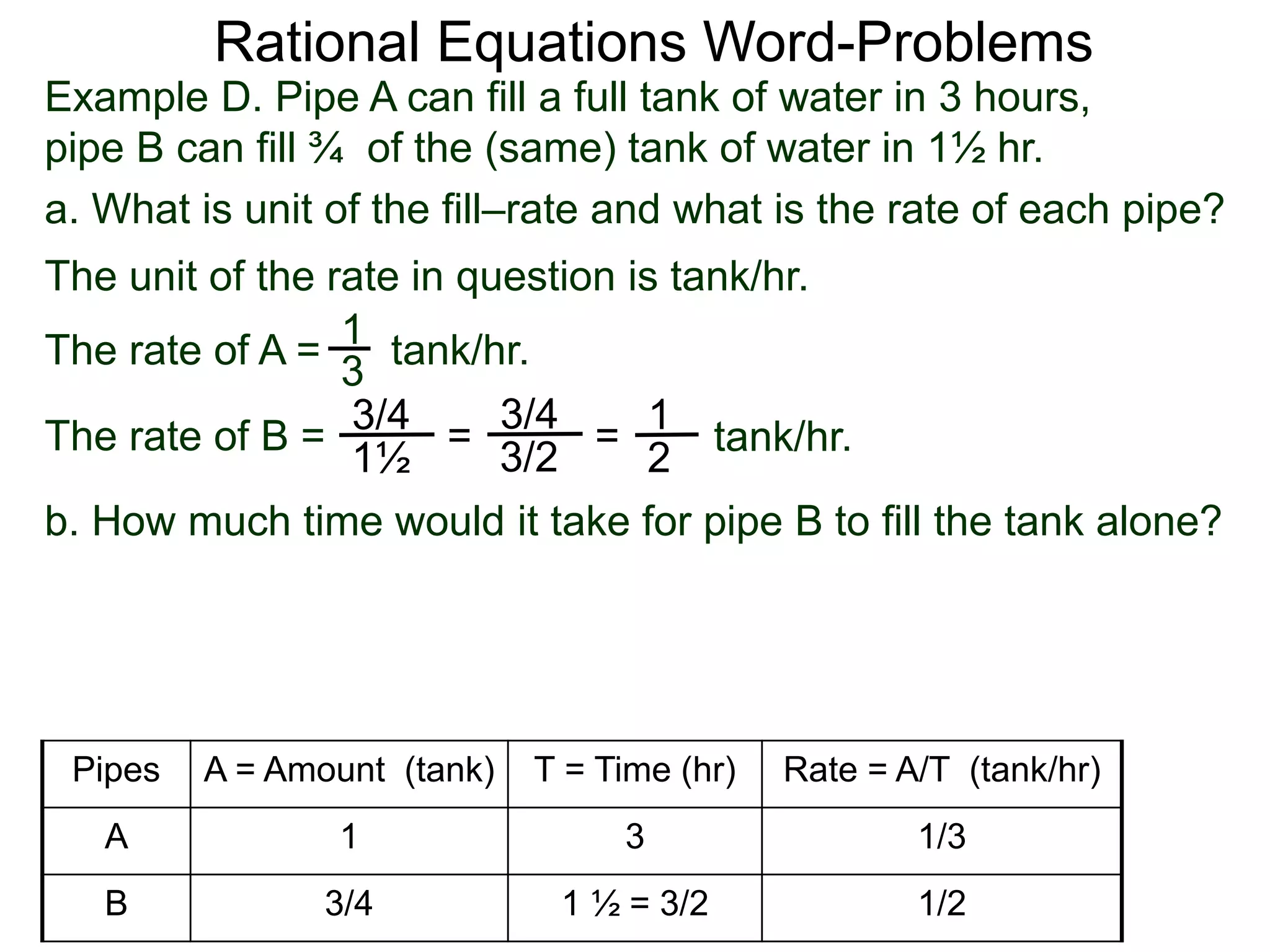
















![Rational Equations Word-Problems
5
6=
1
x
+ 1
(x – 1)
clear the denominatorsx (x – 1)][
Set x = number of hours for A to
fill the tank
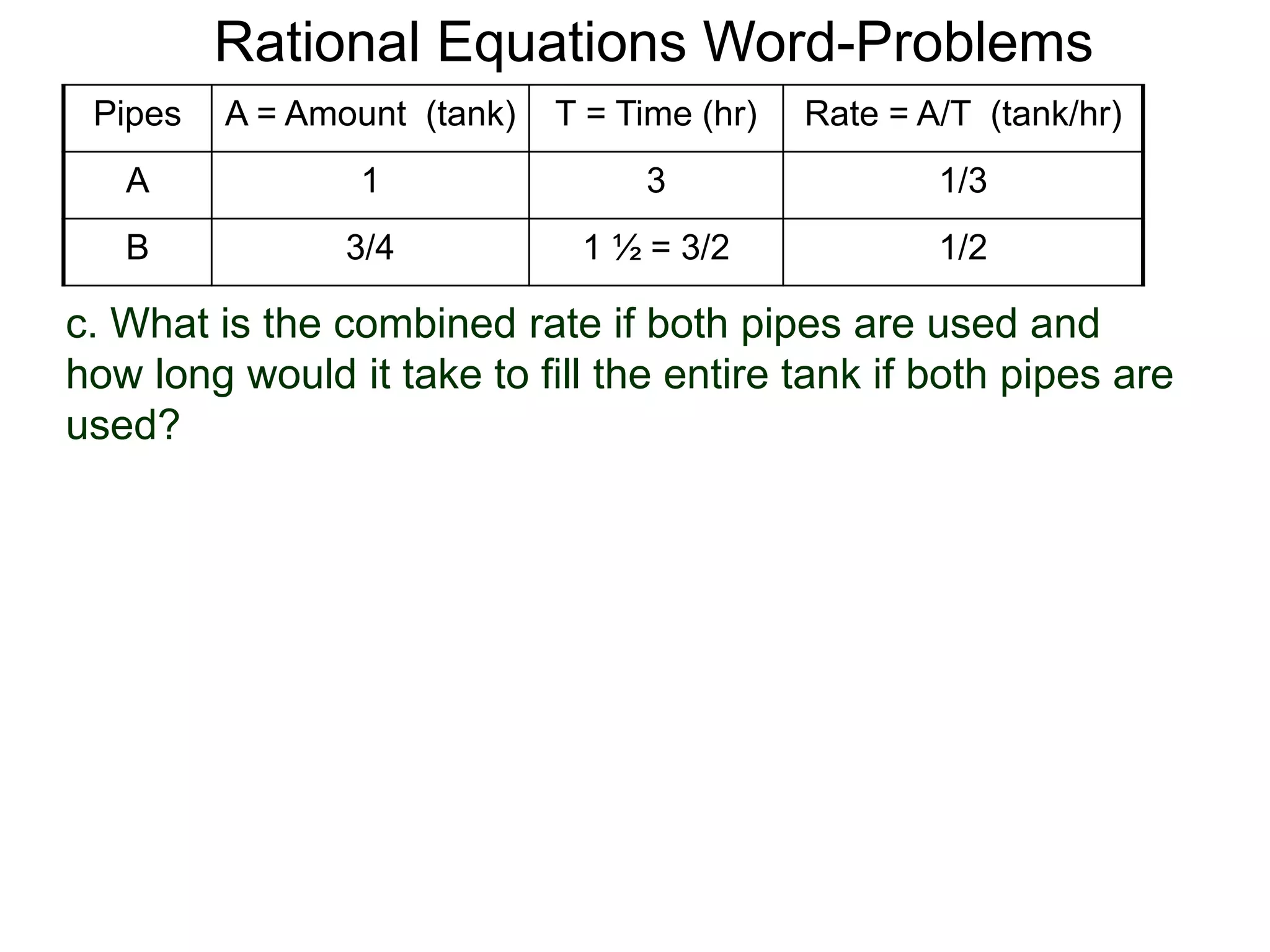
Pipes Time
(hr)
Rate
(tank/hr)
A x 1/x
B (x – 1) 1/(x – 1)
A & B 6/5 5/6
Example E. Pipe B takes one hour less to fill a full tank of
water then pipe A does and together they got the job done in
6/5 hr. How long will it take pipe A to fill the tank alone?
(What should x be?)
So the number of hours for B to
fill the tank is (x – 1)
It takes 6/5 hr to use both. .
Put these into a table. The rates for A and B add to the
combined rate 5/6 so we get a rational equation in x.](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-107-2048.jpg)
![Rational Equations Word-Problems
5
6=
1
x
+ 1
(x – 1)
clear the denominators6x (x – 1)
6x
][
Set x = number of hours for A to
fill the tank
Pipes Time
(hr)
Rate
(tank/hr)
A x 1/x
B (x – 1) 1/(x – 1)
A & B 6/5 5/6
Example E. Pipe B takes one hour less to fill a full tank of
water then pipe A does and together they got the job done in
6/5 hr. How long will it take pipe A to fill the tank alone?
(What should x be?)
So the number of hours for B to
fill the tank is (x – 1)
Put these into a table. The rates for A and B add to the
combined rate 5/6 so we get a rational equation in x.
It takes 6/5 hr to use both. .
6(x – 1) x (x – 1)](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-108-2048.jpg)
![Rational Equations Word-Problems
5
6=
1
x
+ 1
(x – 1)
clear the denominators6x (x – 1)
6x
][
Set x = number of hours for A to
fill the tank
Pipes Time
(hr)
Rate
(tank/hr)
A x 1/x
B (x – 1) 1/(x – 1)
A & B 6/5 5/6
Example E. Pipe B takes one hour less to fill a full tank of
water then pipe A does and together they got the job done in
6/5 hr. How long will it take pipe A to fill the tank alone?
(What should x be?)
So the number of hours for B to
fill the tank is (x – 1)
Put these into a table. The rates for A and B add to the
combined rate 5/6 so we get a rational equation in x.
It takes 6/5 hr to use both. .
6(x – 1) x (x – 1)
6x – 6 + 6x = 5x2 – 5x](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-109-2048.jpg)
![Rational Equations Word-Problems
5
6=
1
x
+ 1
(x – 1)
clear the denominators6x (x – 1)
6x
][
Set x = number of hours for A to
fill the tank
Pipes Time
(hr)
Rate
(tank/hr)
A x 1/x
B (x – 1) 1/(x – 1)
A & B 6/5 5/6
Example E. Pipe B takes one hour less to fill a full tank of
water then pipe A does and together they got the job done in
6/5 hr. How long will it take pipe A to fill the tank alone?
(What should x be?)
So the number of hours for B to
fill the tank is (x – 1)
Put these into a table. The rates for A and B add to the
combined rate 5/6 so we get a rational equation in x.
It takes 6/5 hr to use both. .
6(x – 1) x (x – 1)
6x – 6 + 6x = 5x2 – 5x
0 = 5x2 – 17x + 6
(Question: Why is the other solution no good?)
you finish this...](https://image.slidesharecdn.com/2-4rationalequationsword-problems-110828224446-phpapp02/75/2-5-rational-equations-word-problems-110-2048.jpg)