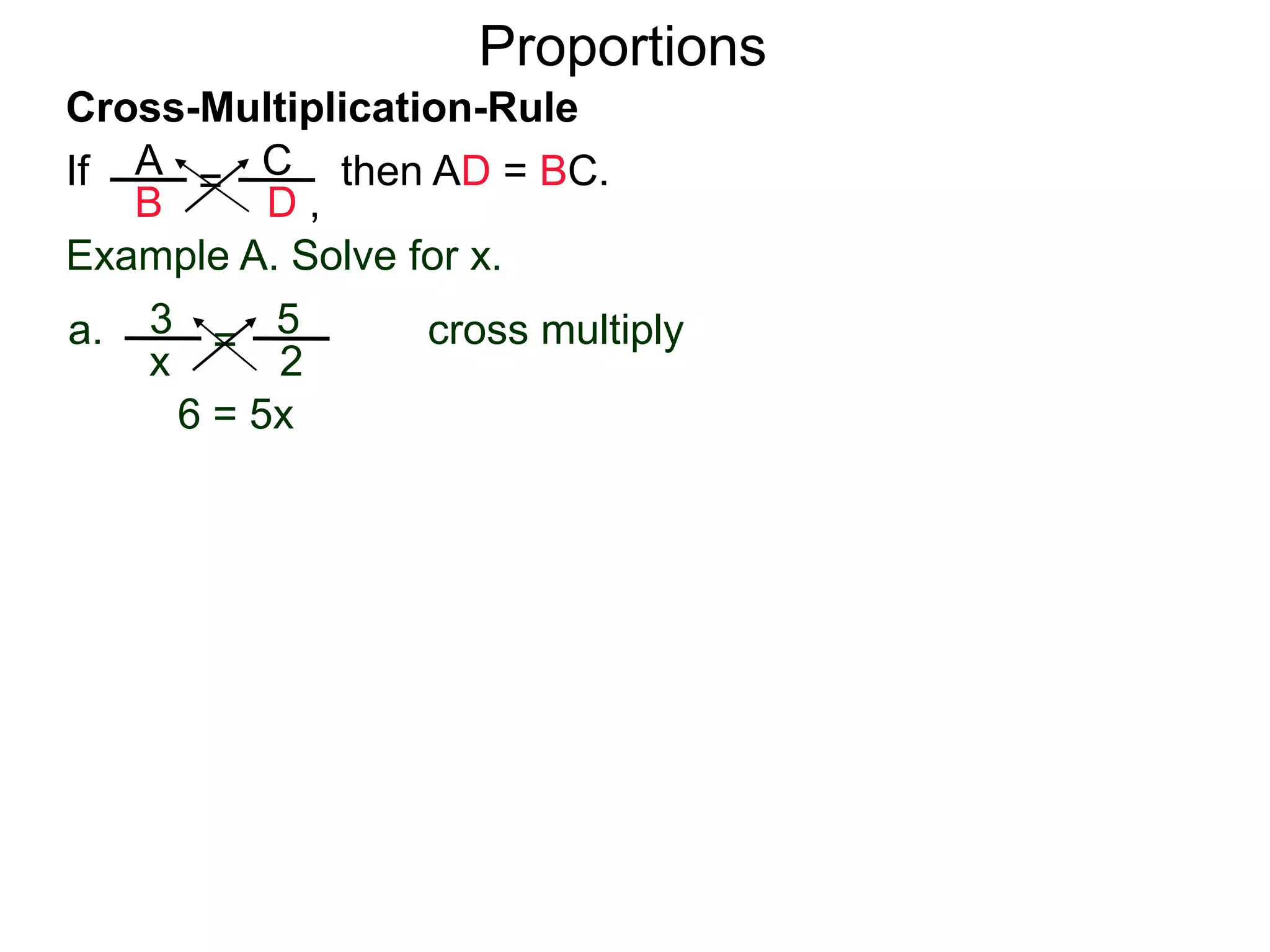
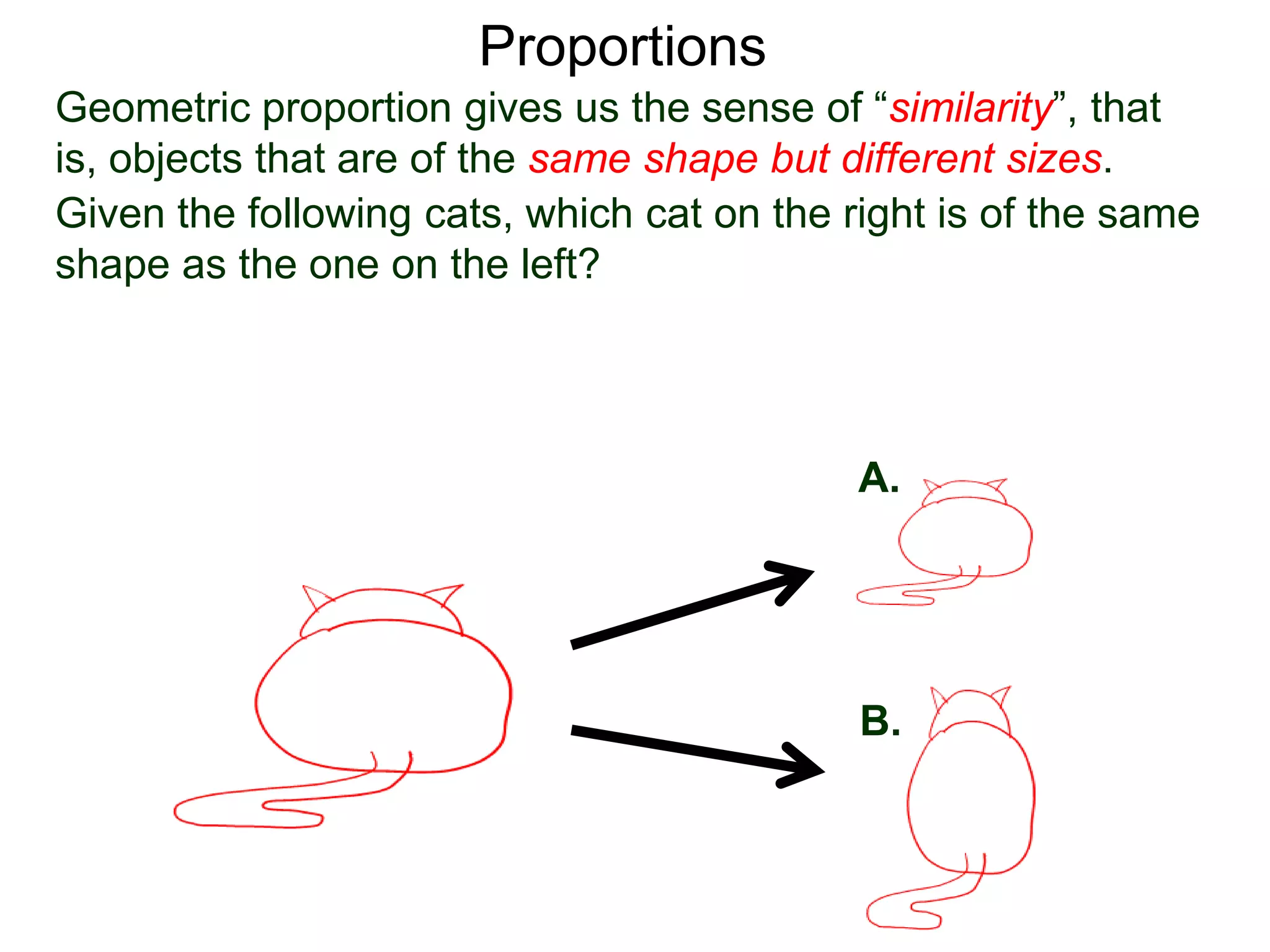
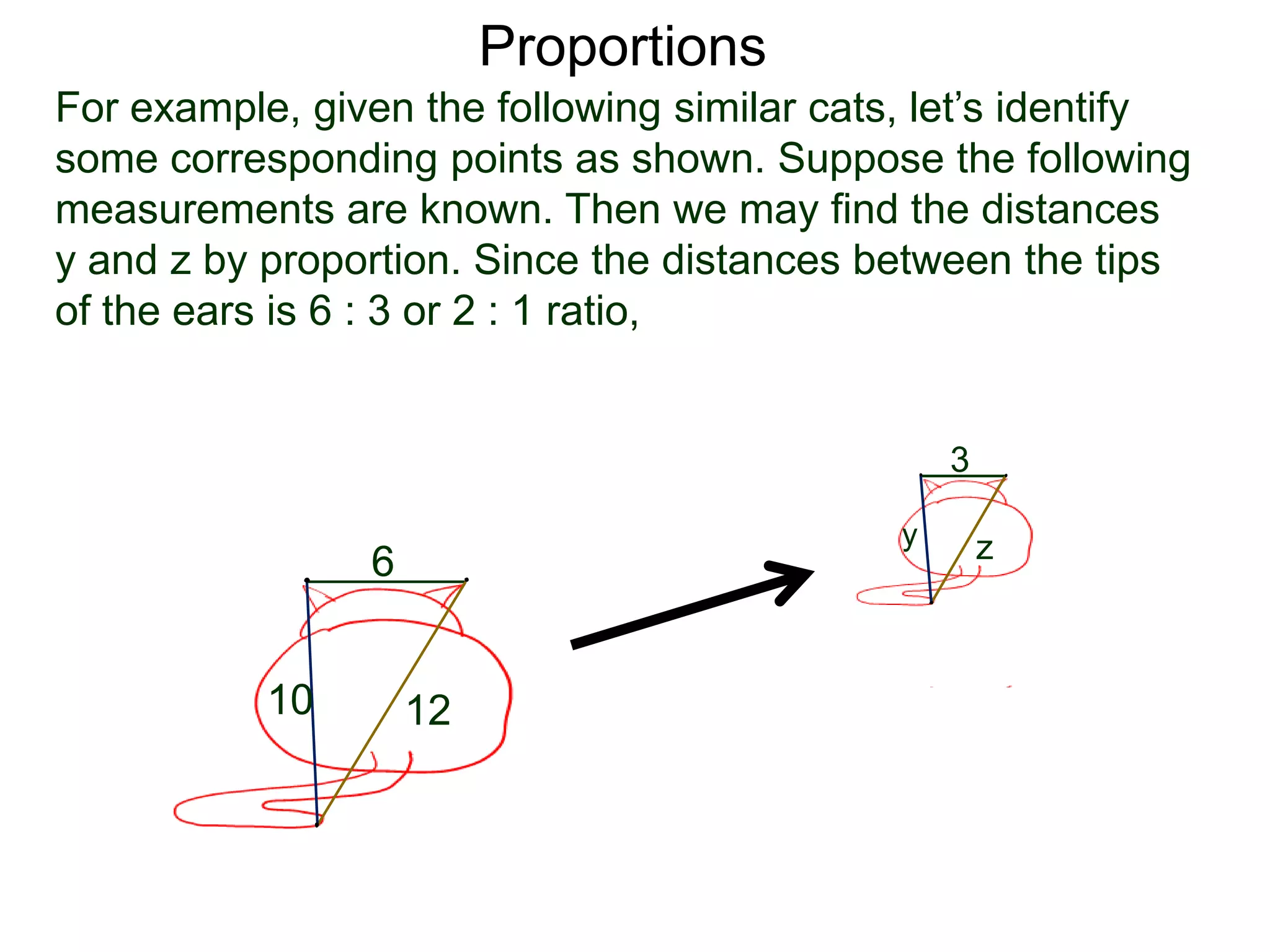
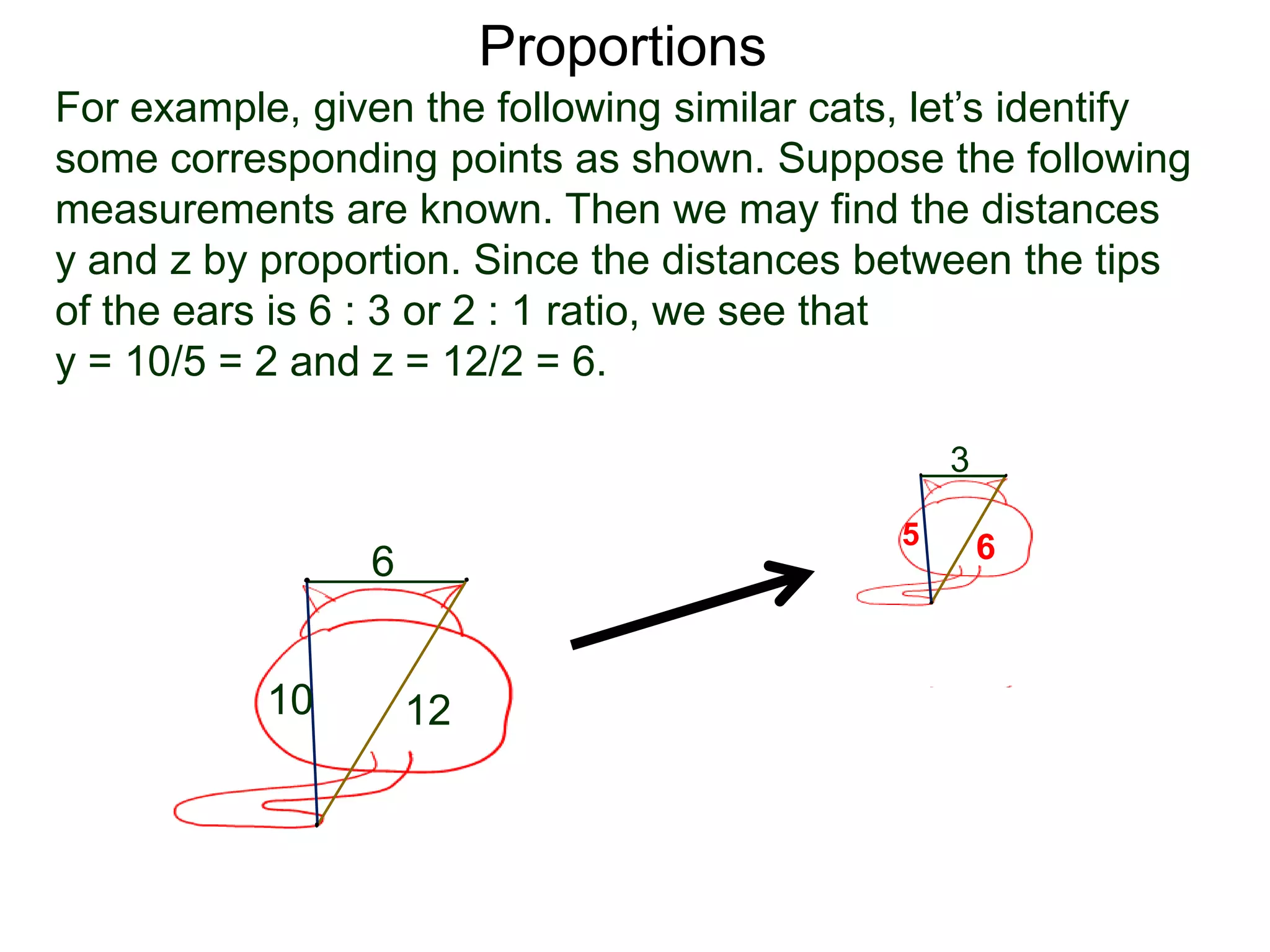
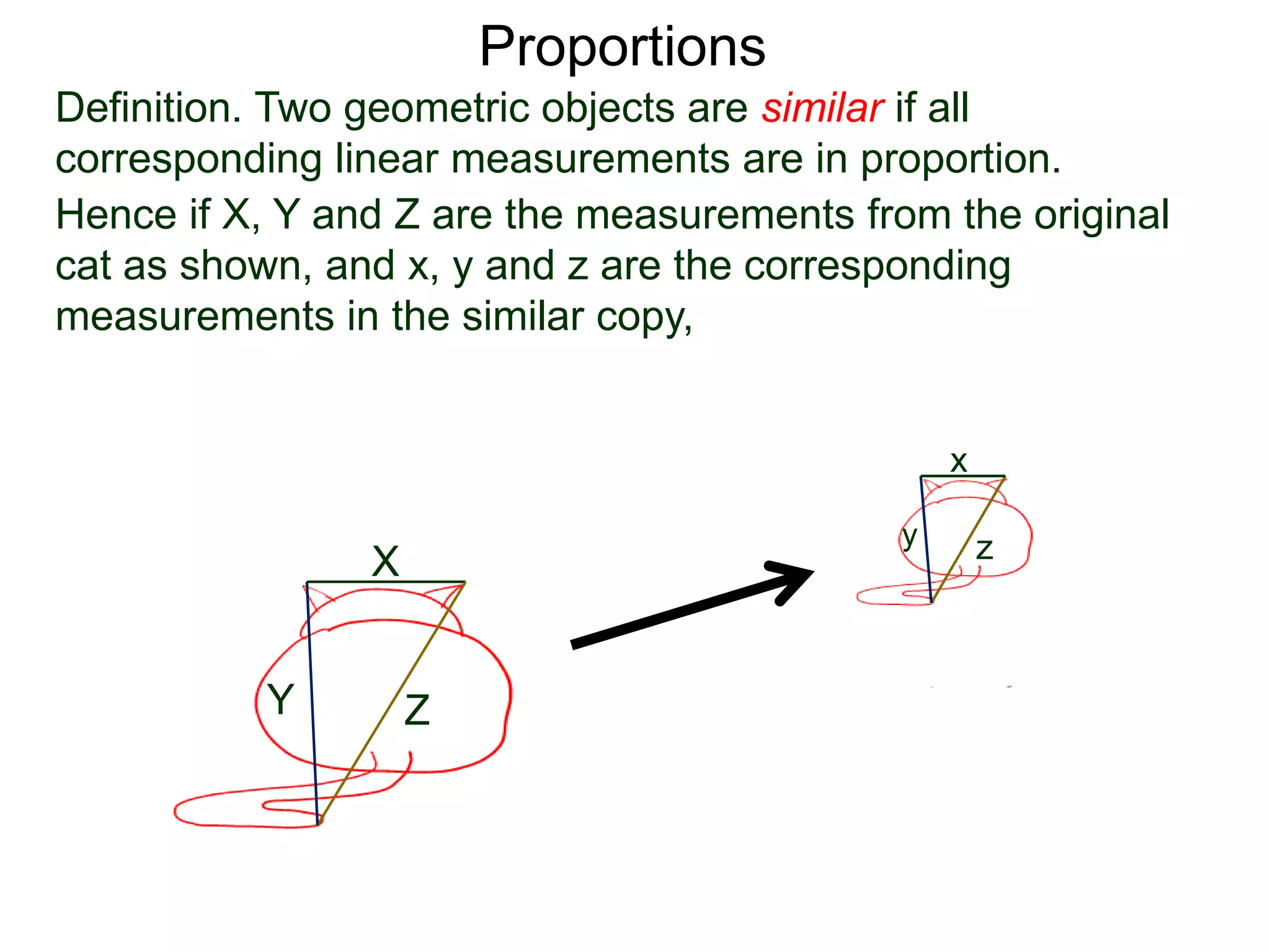
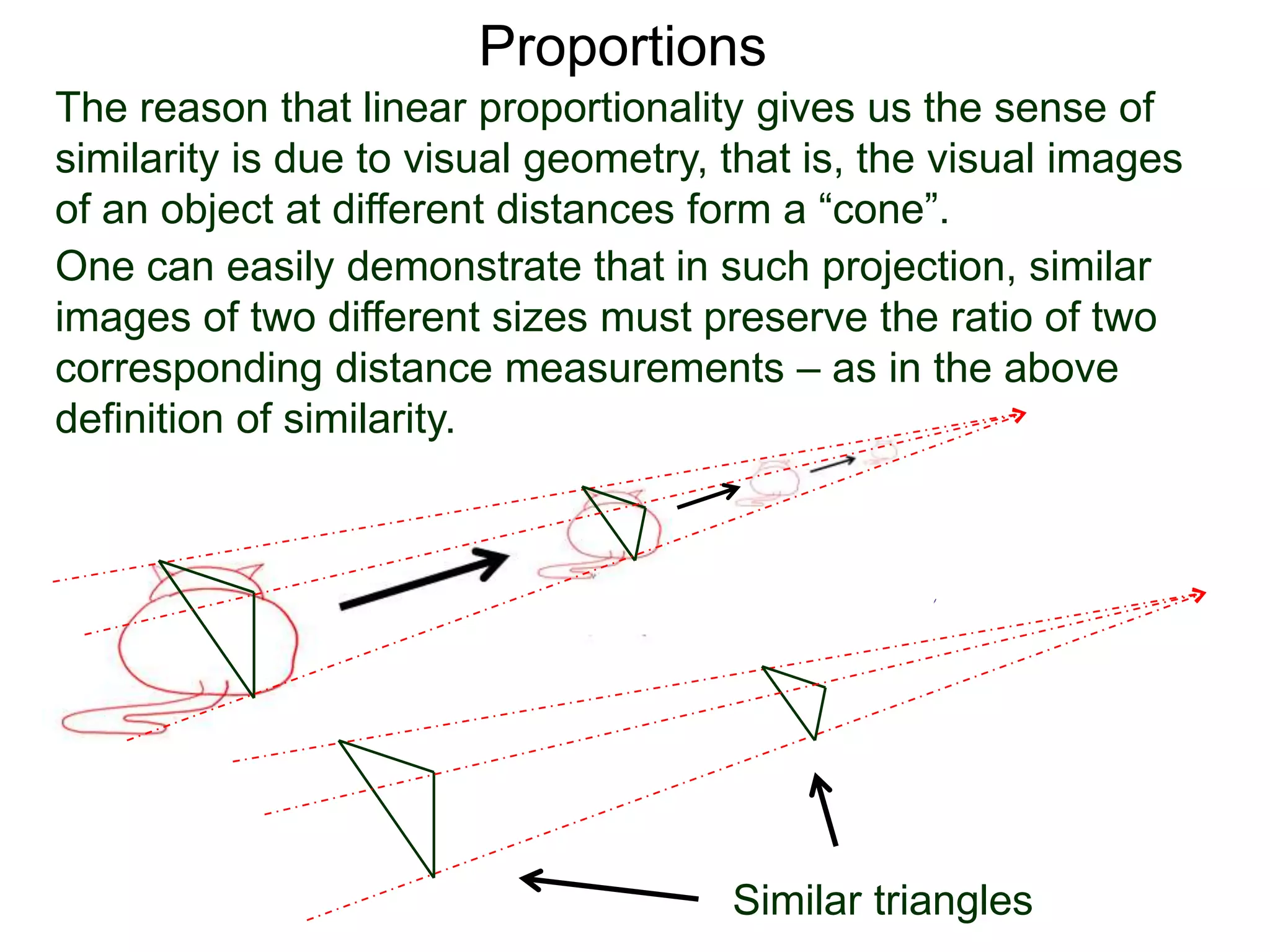
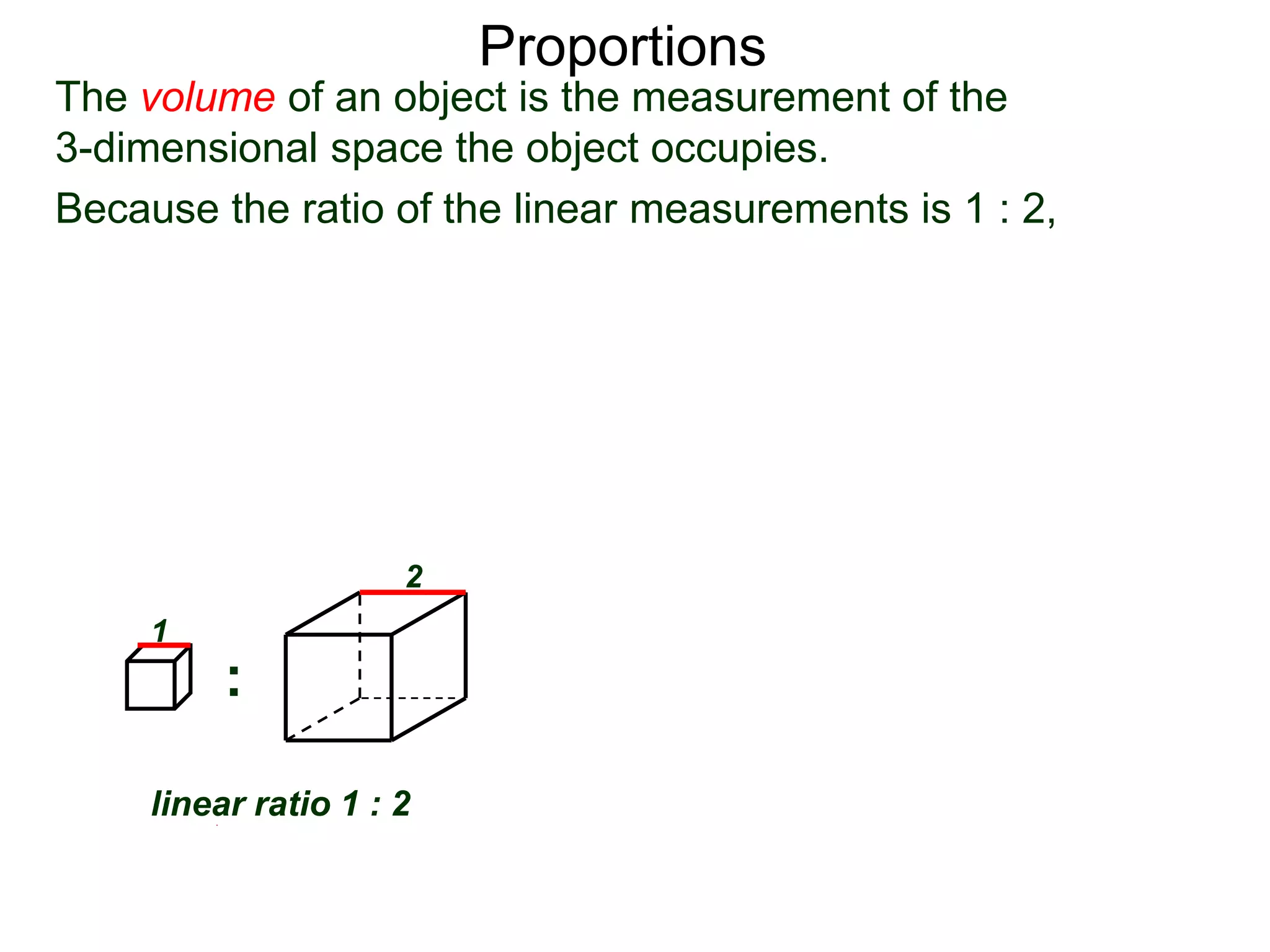
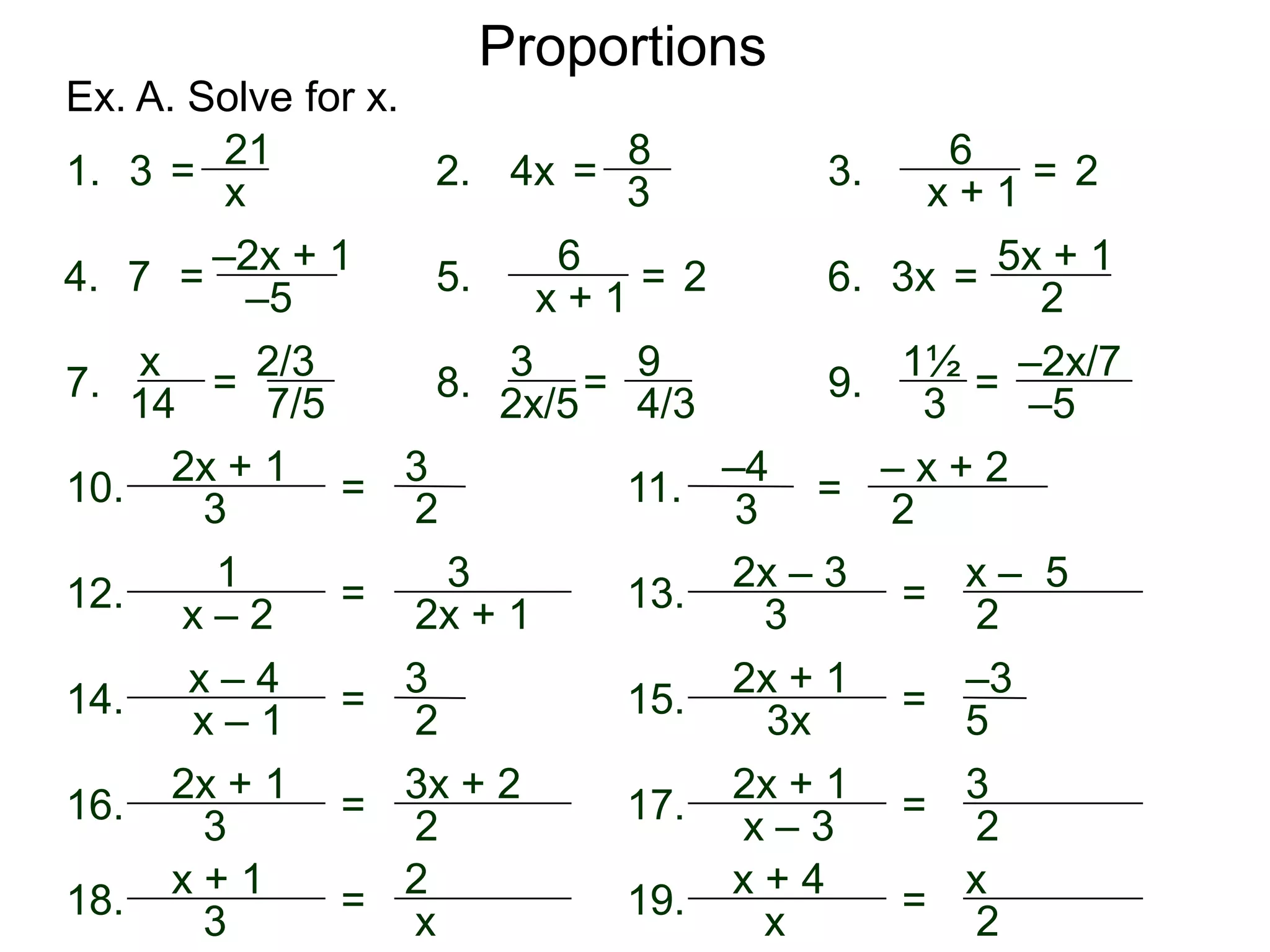
The document discusses ratios and proportions. It defines a ratio as two related quantities stated side by side, and gives an example of a 3:4 ratio of eggs to flour in a recipe. It explains how to write ratios as fractions and set up proportion equations. Proportions are equal ratios, like 3:4 being proportional to 6:8. The document solves sample proportion word problems, like finding the number of eggs needed given 10 cups of flour using a proportion equation.

1. Proportions

2. Proportions
Two related quantities stated side by side is called a ratio.

3. Proportions
Two related quantities stated side by side is called a ratio.
For example, if a recipe calls for 3 eggs and 4 cups of flour,
then the ratio of eggs to flour is 3 to 4.

4. 3
4
eggs
cups of flour
Proportions
Two related quantities stated side by side is called a ratio.
For example, if a recipe calls for 3 eggs and 4 cups of flour,
then the ratio of eggs to flour is 3 to 4.
We may write it using fractional notation as:

5. 3
4
eggs
cups of flour
Proportions
This fraction is also the amount of per unit of the given ratio,
in this case, 3/4 egg / per cup of flour.
Two related quantities stated side by side is called a ratio.
For example, if a recipe calls for 3 eggs and 4 cups of flour,
then the ratio of eggs to flour is 3 to 4.
We may write it using fractional notation as:
(egg / per cup of flour)

6. 3
4
eggs
cups of flour
Proportions
This fraction is also the amount of per unit of the given ratio,
in this case, 3/4 egg / per cup of flour.
Two ratios that are equal are said to be in proportion.
Two related quantities stated side by side is called a ratio.
For example, if a recipe calls for 3 eggs and 4 cups of flour,
then the ratio of eggs to flour is 3 to 4.
We may write it using fractional notation as:
(egg / per cup of flour)

7. 3
4
eggs
cups of flour
Proportions
This fraction is also the amount of per unit of the given ratio,
in this case, 3/4 egg / per cup of flour.
Two ratios that are equal are said to be in proportion.
Thus "3 to 4" is proportion to "6 to 8" since
3
4 =
6
8
Two related quantities stated side by side is called a ratio.
For example, if a recipe calls for 3 eggs and 4 cups of flour,
then the ratio of eggs to flour is 3 to 4.
We may write it using fractional notation as:
(egg / per cup of flour)

8. 3
4
eggs
cups of flour
Proportions
This fraction is also the amount of per unit of the given ratio,
in this case, 3/4 egg / per cup of flour.
Two ratios that are equal are said to be in proportion.
Thus "3 to 4" is proportion to "6 to 8" since
3
4 =
6
8
Proportion–equations are the simplest type of fractional
equations.
Two related quantities stated side by side is called a ratio.
For example, if a recipe calls for 3 eggs and 4 cups of flour,
then the ratio of eggs to flour is 3 to 4.
We may write it using fractional notation as:
(egg / per cup of flour)

9. 3
4
eggs
cups of flour
Proportions
This fraction is also the amount of per unit of the given ratio,
in this case, 3/4 egg / per cup of flour.
Two ratios that are equal are said to be in proportion.
Thus "3 to 4" is proportion to "6 to 8" since
3
4 =
6
8
Proportion–equations are the simplest type of fractional
equations. To solve proportional equations, cross-multiply
and change the proportions into regular equations.
Two related quantities stated side by side is called a ratio.
For example, if a recipe calls for 3 eggs and 4 cups of flour,
then the ratio of eggs to flour is 3 to 4.
We may write it using fractional notation as:
(egg / per cup of flour)

10. A
B
C
D ,
=If
Cross-Multiplication-Rule
Proportions

11. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions

12. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a.

13. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply

14. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x

15. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x
= x5
6

16. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x
= x
2
3
(x + 2)
(x – 5)
=b.
5
6

17. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x
= x5
6
2
3
(x + 2)
(x – 5)
=b. cross multiply

18. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x
= x
2
3
(x + 2)
(x – 5)
=b. cross multiply
2(x – 5) = 3(x + 2)
5
6

19. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x
= x
2
3
(x + 2)
(x – 5)
=b. cross multiply
2(x – 5) = 3(x + 2)
2x – 10 = 3x + 6
5
6

20. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x
= x
2
3
(x + 2)
(x – 5)
=b. cross multiply
2(x – 5) = 3(x + 2)
2x – 10 = 3x + 6
–10 – 6 = 3x – 2x
5
6

21. A
B
C
D ,
=If then AD = BC.
Cross-Multiplication-Rule
Proportions
Example A. Solve for x.
3
x
5
2
=a. cross multiply
6 = 5x
= x
2
3
(x + 2)
(x – 5)
=b. cross multiply
2(x – 5) = 3(x + 2)
2x – 10 = 3x + 6
–10 – 6 = 3x – 2x
–16 = x
5
6

22. Proportions
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions

23. Proportions
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

24. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

25. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour. How
many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed.
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

26. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown.
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

27. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown.
number of eggs
cups of flour
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

28. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown. Then write down the ratios.
number of eggs
cups of flour
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

29. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown. Then write down the ratios.
number of eggs
cups of flour
x
10
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

30. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown. Then write down the ratios.
number of eggs
cups of flour
3
4
x
10
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

31. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown. Then write down the ratios.
number of eggs
cups of flour
3
4
x
10
=
Set them equal, we get
x
10
3
4
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

32. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown. Then write down the ratios.
number of eggs
cups of flour
3
4
x
10
=
Set them equal, we get
x
10
3
4
cross multiply
4x = 30
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

33. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown. Then write down the ratios.
number of eggs
cups of flour
3
4
x
10
=
Set them equal, we get
x
10
3
4
cross multiply
4x = 30
x =
30
4
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

34. Proportions
Example B. A recipe calls for 3 eggs and 4 cups of flour.
How many eggs are needed if we have 10 cups of flour?
Let x be the number of eggs needed. Write the two types of
measurements, the number of eggs and the number of cups
of flour, in a column as shown. Then write down the ratios.
number of eggs
cups of flour
3
4
x
10
=
Set them equal, we get
x
10
3
4
cross multiply
4x = 30
x =
30
4
= 7½ We need 7½ eggs.
When setting up a proportional equation for a word problem,
the two quantities for the same type of measurement must
occupy the same position in the fractions i.e. both must be in
numerator, or both must be in the denominator.

35. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions

36. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as

37. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as
miles
inches

38. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as
miles
inches
x
14

39. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as
miles
inches
21
4
x
14

40. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as
miles
inches
21
4
x
14
Set them equal, we get
21
4
x
14
=

41. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as
miles
inches
21
4
x
14
Set them equal, we get
21
4
x
14
= cross multiply
4x = 294

42. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as
miles
inches
21
4
x
14
Set them equal, we get
21
4
x
14
= cross multiply
4x = 294
x =
294
4

43. Example C. On a map, 4 inches corresponds to 21 miles in
real distance. What is the real distance between two points
if they are 14 inches apart on the map?
Proportions
Let x be the number of real distance in miles and write the
two types of measurements as
miles
inches
21
4
x
14
Set them equal, we get
21
4
x
14
= cross multiply
4x = 294
x =
294
4
= 73½
So 4 inches corresponds to 73½ miles.

44. Proportions
Geometric proportion gives us the sense of “similarity”, that is,
objects that are of the same shape but different sizes.

45. Proportions
Given the following cats, which cat on the right is of the same
shape as the one on the left?
A.
B.
Geometric proportion gives us the sense of “similarity”, that is,
objects that are of the same shape but different sizes.

46. Proportions
Given the following cats, which cat on the right is of the same
shape as the one on the left? The answer of course is A.
A.
B.
Geometric proportion gives us the sense of “similarity”, that is,
objects that are of the same shape but different sizes.

47. Proportions
Given the following cats, which cat on the right is of the same
shape as the one on the left? The answer of course is A.
A.
B.
This sense of similarity is due to the fact that
“all corresponding linear measurements are in proportion”.
Geometric proportion gives us the sense of “similarity”, that is,
objects that are of the same shape but different sizes.

48. Proportions
For example, given the following similar cats,

49. Proportions
For example, given the following similar cats, let’s identify
some corresponding points as shown.

50. Proportions
B.
For example, given the following similar cats, let’s identify
some corresponding points as shown. Suppose the following
measurements are known.
6
10 12

51. Proportions
B.
For example, given the following similar cats, let’s identify
some corresponding points as shown. Suppose the following
measurements are known.
6
10 12
3

52. Proportions
B.
For example, given the following similar cats, let’s identify
some corresponding points as shown. Suppose the following
measurements are known. Then we may find the distances
y and z by proportion.
6
10 12
3
y z

53. Proportions
B.
For example, given the following similar cats, let’s identify
some corresponding points as shown. Suppose the following
measurements are known. Then we may find the distances
y and z by proportion. Since the distances between the tips
of the ears is 6 : 3 or 2 : 1 ratio,
6
10 12
3
y z

54. Proportions
B.
For example, given the following similar cats, let’s identify
some corresponding points as shown. Suppose the following
measurements are known. Then we may find the distances
y and z by proportion. Since the distances between the tips
of the ears is 6 : 3 or 2 : 1 ratio, we see that
y =
6
10 12
3
y z

55. Proportions
B.
For example, given the following similar cats, let’s identify
some corresponding points as shown. Suppose the following
measurements are known. Then we may find the distances
y and z by proportion. Since the distances between the tips
of the ears is 6 : 3 or 2 : 1 ratio, we see that
y = 10/5 = 2 and z = 12/2 = 6.
6
10 12
3
y z

56. Proportions
6
10 12
3
5 6
For example, given the following similar cats, let’s identify
some corresponding points as shown. Suppose the following
measurements are known. Then we may find the distances
y and z by proportion. Since the distances between the tips
of the ears is 6 : 3 or 2 : 1 ratio, we see that
y = 10/5 = 2 and z = 12/2 = 6.

57. Proportions
Definition. Two geometric objects are similar if all
corresponding linear measurements are in proportion.
B.

58. Proportions
Definition. Two geometric objects are similar if all
corresponding linear measurements are in proportion.
B.
Hence if X, Y and Z are the measurements from the original
cat as shown,
X
Y Z

59. Proportions
Definition. Two geometric objects are similar if all
corresponding linear measurements are in proportion.
B.
Hence if X, Y and Z are the measurements from the original
cat as shown, and x, y and z are the corresponding
measurements in the similar copy,
X
Y Z
x
y z

60. Proportions
Definition. Two geometric objects are similar if all
corresponding linear measurements are in proportion.
B.
Hence if X, Y and Z are the measurements from the original
cat as shown, and x, y and z are the corresponding
measurements in the similar copy, then it must be that
X
Y Z
x
y z
X
x =
Y
y =
Z
z

61. Proportions
Definition. Two geometric objects are similar if all
corresponding linear measurements are in proportion.
B.
Hence if X, Y and Z are the measurements from the original
cat as shown, and x, y and z are the corresponding
measurements in the similar copy, then it must be that
X
Y Z
x
y z
X
x =
Y
y =
Z
z
or that X
Y =
x
y etc…

62. Proportions
Definition. Two geometric objects are similar if all
corresponding linear measurements are in proportion.
B.
Hence if X, Y and Z are the measurements from the original
cat as shown, and x, y and z are the corresponding
measurements in the similar copy, then it must be that
X
Y Z
x
y z
X
x =
Y
y =
Z
z
or that X
Y =
x
y etc…
This mathematical formulation of similarity is the basis for
biometric security software such as facial recognition systems.

63. Proportions
The reason that linear proportionality gives us the sense of
similarity is due to visual geometry, that is, the visual images
of an object at different distances form a “cone”.

64. Proportions
The reason that linear proportionality gives us the sense of
similarity is due to visual geometry, that is, the visual images
of an object at different distances form a “cone”.

65. Proportions
The reason that linear proportionality gives us the sense of
similarity is due to visual geometry, that is, the visual images
of an object at different distances form a “cone”.
One can easily demonstrate that in such projection, similar
images of two different sizes must preserve the ratio of two
corresponding distance measurements – as in the above
definition of similarity.

66. Proportions
The reason that linear proportionality gives us the sense of
similarity is due to visual geometry, that is, the visual images
of an object at different distances form a “cone”.
One can easily demonstrate that in such projection, similar
images of two different sizes must preserve the ratio of two
corresponding distance measurements – as in the above
definition of similarity.
Similar triangles

67. Proportions
In the definition of similarity, the measurements in proportion
must be linear.

68. Proportions
In the definition of similarity, the measurements in proportion
must be linear. It's not true that the ratio of areas is
proportional to linear ratio of two similar objects.

69. Proportions
In the definition of similarity, the measurements in proportion
must be linear. It's not true that the ratio of areas is
proportional to linear ratio of two similar objects.
Because the ratio of the linear measurements is 1 : 2,
1
2

70. Proportions
In the definition of similarity, the measurements in proportion
must be linear. It's not true that the ratio of areas is
proportional to linear ratio of two similar objects.
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the area–measurements is
1 : (2)2 or 1 : 4 ratio.
1
2
linear ratio 1 : 2
area–ratio 1 : 4 = 22
:

71. Proportions
1
2
linear ratio 1 : 2
area–ratio 1 : 4 = 22
:
In the definition of similarity, the measurements in proportion
must be linear. It's not true that the ratio of areas is
proportional to linear ratio of two similar objects.
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the area–measurements is
1 : (2)2 or 1 : 4 ratio. So it would take 4 times as much paint to
paint the larger one.

72. Proportions
1
2
linear ratio 1 : 2
area–ratio 1 : 4 = 22
linear ratio 1 : r
area–ratio 1 : r2
1
r
: :
In the definition of similarity, the measurements in proportion
must be linear. It's not true that the ratio of areas is
proportional to linear ratio of two similar objects.
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the area–measurements is
1 : (2)2 or 1 : 4 ratio. So it would take 4 times as much paint to
paint the larger one. Given two similar objects with linear
ratio 1 : r then their area–ratio is 1 : r2.

73. Proportions
1
2
linear ratio 1 : 2
area–ratio 1 : 4 = 22
linear ratio 1 : r
area–ratio 1 : r2
1
r
: :
In the definition of similarity, the measurements in proportion
must be linear. It's not true that the ratio of areas is
proportional to linear ratio of two similar objects.
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the area–measurements is
1 : (2)2 or 1 : 4 ratio. So it would take 4 times as much paint to
paint the larger one. Given two similar objects with linear
ratio 1 : r then their area–ratio is 1 : r2. This is also true for
the surface areas.

74. Proportions
1
2
linear ratio 1 : 2
area–ratio 1 : 4 = 22
linear ratio 1 : r
area–ratio 1 : r2
1
r
: :
In the definition of similarity, the measurements in proportion
must be linear. It's not true that the ratio of areas is
proportional to linear ratio of two similar objects.
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the area–measurements is
1 : (2)2 or 1 : 4 ratio. So it would take 4 times as much paint to
paint the larger one. Given two similar objects with linear
ratio 1 : r then their area–ratio is 1 : r2. This is also true for
the surface areas i.e. two similar 3D solids of 1 : r linear
ratio have 1 : r2 as their surface–area ratio.

75. Proportions
The volume of an object is the measurement of the
3-dimensional space the object occupies.

76. Proportions
Because the ratio of the linear measurements is 1 : 2,
:
linear ratio 1 : 2
1
2
The volume of an object is the measurement of the
3-dimensional space the object occupies.

77. Proportions
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the volume–measurements
is 1 : (2)3 or 1 : 8 ratio.
:
linear ratio 1 : 2
volume–ratio 1 : 8 = 23
1
2
The volume of an object is the measurement of the
3-dimensional space the object occupies.

78. Proportions
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the volume–measurements
is 1 : (2)3 or 1 : 8 ratio. So the weight of large one is 8 times
as much as the small one (if they are made of the same
thing).*
:
linear ratio 1 : 2
volume–ratio 1 : 8 = 23
1
2
The volume of an object is the measurement of the
3-dimensional space the object occupies.

79. Proportions
Because the ratio of the linear measurements is 1 : 2,
we may conclude that the ratio of the volume–measurements
is 1 : (2)3 or 1 : 8 ratio. So the weight of large one is 8 times
as much as the small one (if they are made of the same
thing).* Given two similar objects with linear ratio 1 : r
then their volume–ratio is 1 : r3.
linear ratio 1 : r
volume–ratio 1 : r3
::
linear ratio 1 : 2
volume–ratio 1 : 8 = 23
1
2 1
r
The volume of an object is the measurement of the
3-dimensional space the object occupies.

80. The Golden Ratio
Proportions

81. The Golden Ratio
Proportions
An important ratio in arts and science is the golden ratio.

82. The Golden Ratio
Proportions
An important ratio in arts and science is the golden ratio.
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,

83. The Golden Ratio
Proportions
An important ratio in arts and science is the golden ratio.
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1

84. The Golden Ratio
Proportions
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L
An important ratio in arts and science is the golden ratio.

85. The Golden Ratio
Proportions
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L
An important ratio in arts and science is the golden ratio.
1
L

86. The Golden Ratio
Proportions
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L s
An important ratio in arts and science is the golden ratio.
L
s
1
L =

87. The Golden Ratio
Proportions
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L s
An important ratio in arts and science is the golden ratio.
L
s
1
L =
The ratio1/L is the Golden Ratio.

88. The Golden Ratio
Proportions
L
(1 – L)
1
L
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L s
An important ratio in arts and science is the golden ratio.
L
s
1
L =
Since s = 1 – L, we’ve
=
The ratio1/L is the Golden Ratio.

89. The Golden Ratio
Proportions
L
(1 – L)
1
L
cross multiply
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L s
An important ratio in arts and science is the golden ratio.
L
s
1
L =
Since s = 1 – L, we’ve
=
1 – L
=
L2
The ratio1/L is the Golden Ratio.

90. The Golden Ratio
Proportions
L
(1 – L)
1
L
cross multiply
0 = L2 + L – 1
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L s
An important ratio in arts and science is the golden ratio.
L
s
1
L =
Since s = 1 – L, we’ve
=
1 – L
=
L2
The ratio1/L is the Golden Ratio.

91. The Golden Ratio
Proportions
L
(1 – L)
1
L
cross multiply
0 = L2 + L – 1
Cut a line segment of length 1 into two, a long one L and a
short one s such that the ratio of “1 to L” is the same as
“L to s”,
1
L s
An important ratio in arts and science is the golden ratio.
L
s
1
L =
Since s = 1 – L, we’ve
=
1 – L
=
L2
We’ll see later that the answer for L is about 0.618.
http://en.wikipedia.org/wiki/Golden_ratio
http://en.wikipedia.org/wiki/Golden_spiral
The ratio1/L is the Golden Ratio.

92. Ex. A. Solve for x.
Proportions
3
2
2x + 1
3
=
21
x
3 =1.
–2x/7
–5
1½
3
=9.
2.
6
2=3.
x + 1
–57 =4. –2x + 1 6
=5. x + 1 23x =6. 5x + 1
3
4x =
8
2/3
7/5
x
14
=7.
9
4/3
3
2x/5
=8.
10. – x + 2
2
–4
3 =11.
3
2x + 1
1
x – 2
=12.
x – 5
2
2x – 3
3
=13.
3
2
x – 4
x – 1
=14.
–3
5
2x + 1
3x
=15.
3x + 2
2
2x + 1
3
=16. 3
2
2x + 1
x – 3
=17.
2
x
x + 1
3
=18.
x
2
x + 4
x
=19.
1
2

93. Ex. B. (Solve each problem. It’s easier if fractional proportions
are rewritten as proportions of integers.)
Proportions
20. If 4 cups of flour need 3 tsp of salt,
then 10 cups flour need how much of salt?
Different cookie recipes are given, find the missing amounts.
21. If 5 cups of flour need 7 cups of water
then 10 cups water need how much of flour?
23. If 2 ½ tsp of butter flour need 3/4 tsp of salt,
then 6 tsp of salt need how much of flour.
22. If 5 cups of flour need 7 cups of water
then 10 cups flour need how much of water?
24. If 1¼ inches equals 5 miles real distance, how many
miles is 5 inches on the map?
For the given map scales below, find the missing amounts.
25. If 2½ inches equals 140 miles real distance, how many
inches on the map correspond to the distance of 1,100 miles?

94. Proportions
A. B. C.
3
4
1
5
5
6
26. x
20 x
20
6
27.
x
3x + 4 2xx+2
15 x
x
2x – 3
28.
29. 30. 31.
32–37. Find the surface areas of each cat above if A’s surface
area is 2 ft2, B’s surfaces area is 7 ft2. and C’s is 280 ft2?
Ex. C. 26 – 31. Solve for x. Use the given A, B and C,.
38–43. Find the weight of each cat above if cat A is 20 lbs,
cat B is 8 lb. and cat C is 350 lb?