The document discusses mathematical expressions and polynomials. It provides examples of algebraic expressions and operations with polynomials, such as factoring polynomials. Factoring polynomials makes it easier to calculate outputs, simplify rational expressions, and solve equations. One example factors the polynomial 2x3 - 5x2 + 2x and shows it is easier to evaluate the factored form for different values of x than the original polynomial. The key purposes of factoring polynomials are to simplify calculations and operations.





















![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)] Insert [ ]
The point of this problem is
how to subtract a “product”.](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-22-320.jpg)
![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)]
= 2x2 + x – 15 – [3x2 + 11x – 20]
Insert [ ]
remove [ ]](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-23-320.jpg)
![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)]
= 2x2 + x – 15 – [3x2 + 11x – 20]
= 2x2 + x – 15 – 3x2 – 11x + 20
Insert [ ]
remove [ ]](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-24-320.jpg)
![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)]
= 2x2 + x – 15 – [3x2 + 11x – 20]
= 2x2 + x – 15 – 3x2 – 11x + 20
= –x2 – 10x + 5
Insert [ ]
remove [ ]](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-25-320.jpg)
![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)]
= 2x2 + x – 15 – [3x2 + 11x – 20]
= 2x2 + x – 15 – 3x2 – 11x + 20
= –x2 – 10x + 5
Insert [ ]
remove [ ]](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-26-320.jpg)
![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)]
= 2x2 + x – 15 – [3x2 + 11x – 20]
= 2x2 + x – 15 – 3x2 – 11x + 20
= –x2 – 10x + 5
Insert [ ]
remove [ ]
(2x – 5)(x +3) – (3x – 4)(x + 5)
= (2x – 5)(x +3) + (–3x + 4)(x + 5)
= …
Or distribute the minus sign and
change it to an addition problem:](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-27-320.jpg)
![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)]
= 2x2 + x – 15 – [3x2 + 11x – 20]
= 2x2 + x – 15 – 3x2 – 11x + 20
= –x2 – 10x + 5
Insert [ ]
To factor an expression
means to write it as a product
in a non-obvious way.
remove [ ]
(2x – 5)(x +3) – (3x – 4)(x + 5)
= (2x – 5)(x +3) + (–3x + 4)(x + 5)
= …
Or distribute the minus sign and
change it to an addition problem:](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-28-320.jpg)
![Polynomial Expressions
Following are examples of operations with
polynomials and rational expressions.
Example A. Expand and simplify.
(2x – 5)(x +3) – [(3x – 4)(x + 5)]
= 2x2 + x – 15 – [3x2 + 11x – 20]
= 2x2 + x – 15 – 3x2 – 11x + 20
= –x2 – 10x + 5
Insert [ ]
A3 B3 = (A B)(A2 AB + B2)
Important Factoring Formulas:
To factor an expression
means to write it as a product
in a non-obvious way.
A2 – B2 = (A + B)(A – B)
+–
+– +–
remove [ ]
(2x – 5)(x +3) – (3x – 4)(x + 5)
= (2x – 5)(x +3) + (–3x + 4)(x + 5)
= …
Or distribute the minus sign and
change it to an addition problem:](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-29-320.jpg)












![Example C. Evaluate 2x3 – 5x2 + 2x for x = –2, –1, 3
by factoring it first.
2x3 – 5x2 + 2x = x(2x2 – 5x + 2)
= x(2x – 1)(x – 2)
Plug in x = –2:
–2 [2(–2) – 1] [(–2) – 2]
Evaluate Polynomial Expressions
It's easier to evaluate factored polynomial
expressions. It takes fewer steps then plugging in
the values directly.](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-42-320.jpg)
![Example C. Evaluate 2x3 – 5x2 + 2x for x = –2, –1, 3
by factoring it first.
2x3 – 5x2 + 2x = x(2x2 – 5x + 2)
= x(2x – 1)(x – 2)
Plug in x = –2:
–2 [2(–2) – 1] [(–2) – 2] = –2 [–5] [–4] = –40
Evaluate Polynomial Expressions
It's easier to evaluate factored polynomial
expressions. It takes fewer steps then plugging in
the values directly.](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-43-320.jpg)
![Example C. Evaluate 2x3 – 5x2 + 2x for x = –2, –1, 3
by factoring it first.
2x3 – 5x2 + 2x = x(2x2 – 5x + 2)
= x(2x – 1)(x – 2)
Plug in x = –2:
–2 [2(–2) – 1] [(–2) – 2] = –2 [–5] [–4] = –40
Plug in x = –1:
–1 [2(–1) – 1] [(–1) – 2]
Evaluate Polynomial Expressions
It's easier to evaluate factored polynomial
expressions. It takes fewer steps then plugging in
the values directly.](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-44-320.jpg)
![Example C. Evaluate 2x3 – 5x2 + 2x for x = –2, –1, 3
by factoring it first.
2x3 – 5x2 + 2x = x(2x2 – 5x + 2)
= x(2x – 1)(x – 2)
Plug in x = –2:
–2 [2(–2) – 1] [(–2) – 2] = –2 [–5] [–4] = –40
Plug in x = –1:
–1 [2(–1) – 1] [(–1) – 2] = –1 [–3] [–3] = –9
Evaluate Polynomial Expressions
It's easier to evaluate factored polynomial
expressions. It takes fewer steps then plugging in
the values directly.](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-45-320.jpg)
![Example C. Evaluate 2x3 – 5x2 + 2x for x = –2, –1, 3
by factoring it first.
2x3 – 5x2 + 2x = x(2x2 – 5x + 2)
= x(2x – 1)(x – 2)
Plug in x = –2:
–2 [2(–2) – 1] [(–2) – 2] = –2 [–5] [–4] = –40
Plug in x = –1:
–1 [2(–1) – 1] [(–1) – 2] = –1 [–3] [–3] = –9
Plug in x = 3:
3 [2(3) – 1] [(3) – 2] = 3 [5] [1] = 15
Evaluate Polynomial Expressions
It's easier to evaluate factored polynomial
expressions. It takes fewer steps then plugging in
the values directly.](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-46-320.jpg)

















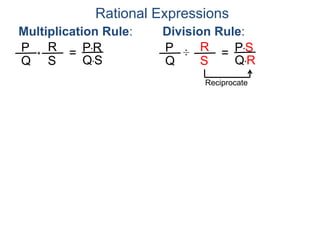

























![Rational Expressions
–
(y2 + 2y – 3)(y2 + y – 2)
2y – 1 y – 3
y2 + y – 2 = (y – 1)(y + 2)
y2 + 2y – 3 = (y – 1)(y + 3)
Hence the LCD = (y – 1)(y + 2)(y + 3),
multiplying LCD/LCD (= 1) to the problem,
–
(y2 + 2y – 3)(y – 1)(y + 2)
2y – 1 y – 3[ ]
Example I. Combine](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-90-320.jpg)
(y + 2)(y + 3)
Example I. Combine
LCD](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-91-320.jpg)
(y + 2)(y + 3)
Example I. Combine
LCD
expand and simplify.
(y – 1)(y + 3)](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-92-320.jpg)
(y + 2)(y + 3)
(y + 3)
Example I. Combine
LCD
expand and simplify.
(y – 1)(y + 3)](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-93-320.jpg)
(y + 2)(y + 3)
(y + 3) (y + 2)
Example I. Combine
LCD
expand and simplify.
(y – 1)(y + 3)](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-94-320.jpg)
(y + 2)(y + 3)
= (2y – 1)(y + 3) – (y – 3)(y + 2)
(y + 3) (y + 2)
Example I. Combine
LCD
LCD
expand and simplify.
(y – 1)(y + 3)](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-95-320.jpg)
(y + 2)(y + 3)
= (2y – 1)(y + 3) – (y – 3)(y + 2) = y2 + 6y + 3
(y + 3) (y + 2)
Example I. Combine
LCD
LCDLCD
expand and simplify.
(y – 1)(y + 3)](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-96-320.jpg)
(y + 2)(y + 3)
= (2y – 1)(y + 3) – (y – 3)(y + 2) = y2 + 6y + 3
So –
(y2 + 2y – 3)(y2 + y – 2)
2y – 1 y – 3
=
y2 + 6y + 3
(y – 1)(y + 2)(y + 3)
(y + 3) (y + 2)
Example I. Combine
LCD
LCDLCD
expand and simplify.
(y – 1)(y + 3)](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-97-320.jpg)











![Rational Expressions
Example K. Simplify
–
(x – h)
1
A complex fraction is a fraction of fractions.
To simplify a complex fraction, use the LCD to clear
all the denominators of all the fractioned terms.
(x + h)
1
2h
Multiply the top and bottom by (x – h)(x + h) to reduce the
expression in the numerators to polynomials.
–
(x – h)
1
(x + h)
1
2h
=
–
(x – h)
1
(x + h)
1
2h
(x + h)(x – h)[ ]
(x + h)(x – h)*
=
–(x + h) (x – h)
2h(x + h)(x – h)
=
2h
2h(x + h)(x – h)
=
1
(x + h)(x – h)](https://image.slidesharecdn.com/1-200702185806/85/1-2-algebraic-expressions-y-109-320.jpg)
















