Embed presentation
Downloaded 232 times


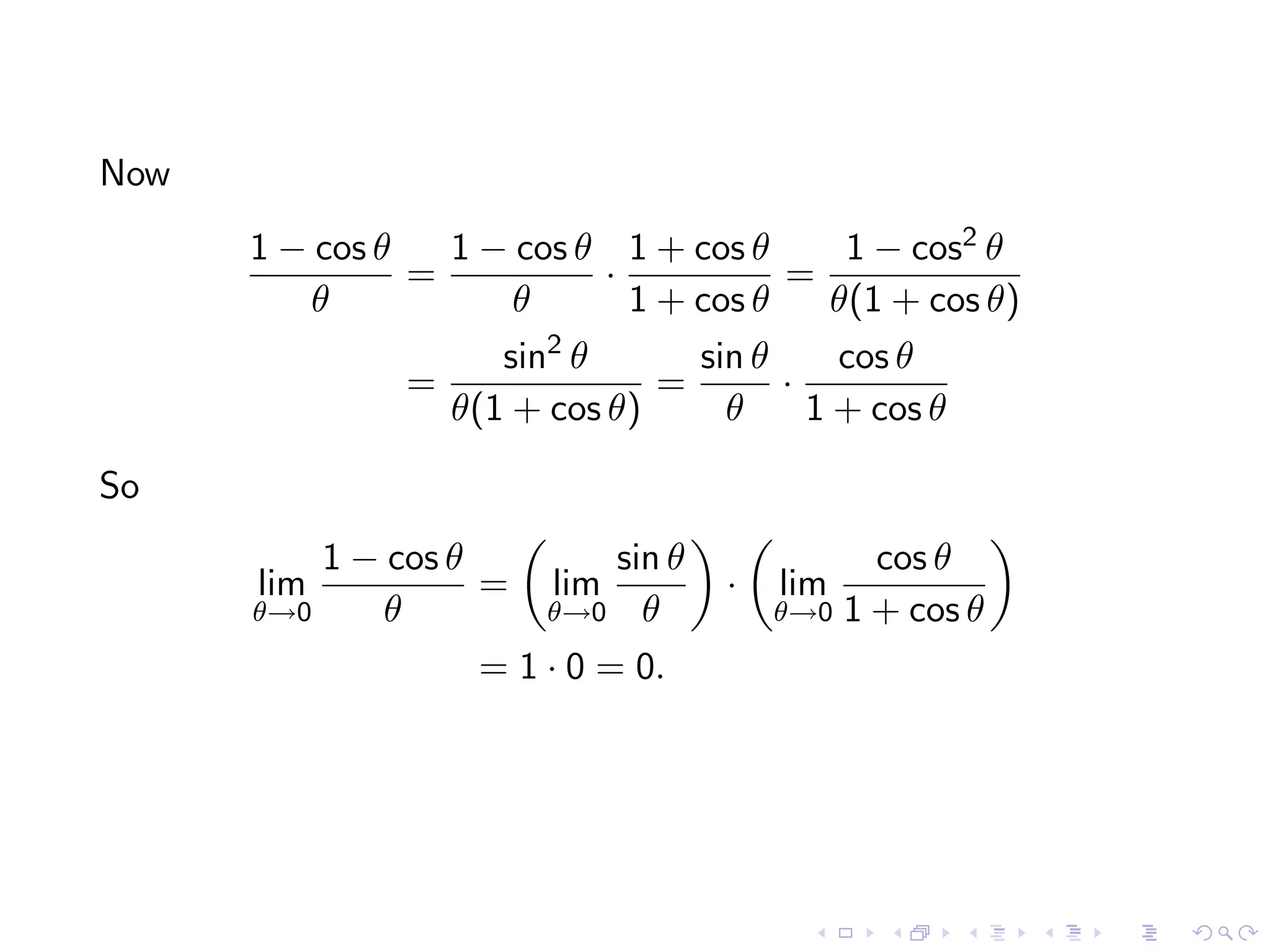














The document outlines the derivatives of trigonometric functions, particularly focusing on sine and cosine, including key limits and proofs. It lists important trigonometric limits, provides derived formulas for sine and cosine, and includes definitions and examples of tangent, secant, cotangent, and cosecant derivatives. Additionally, it mentions problem sessions and office hours for math assistance.



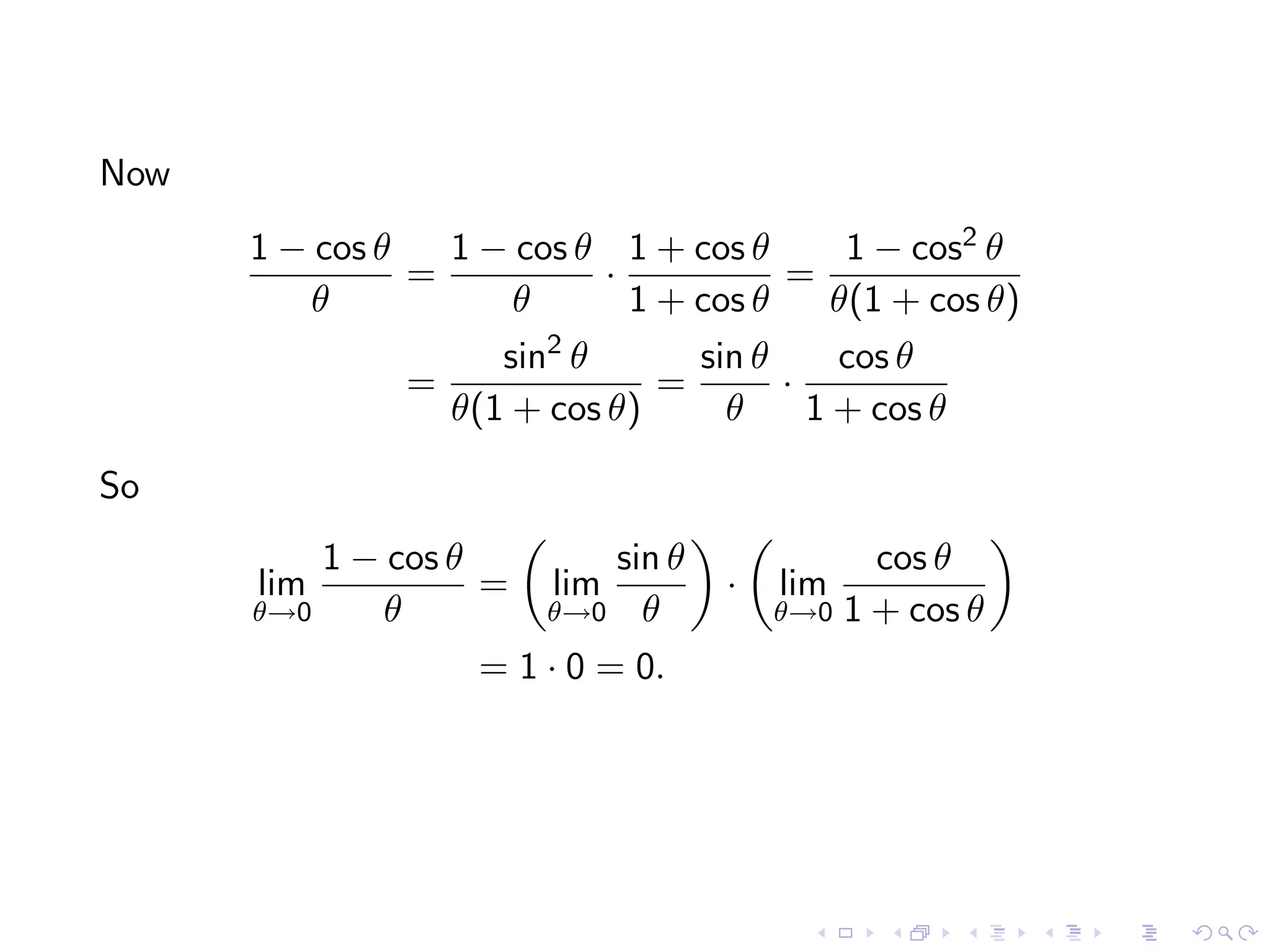
















Introduction to derivatives of sine and cosine functions, with limits and proofs.
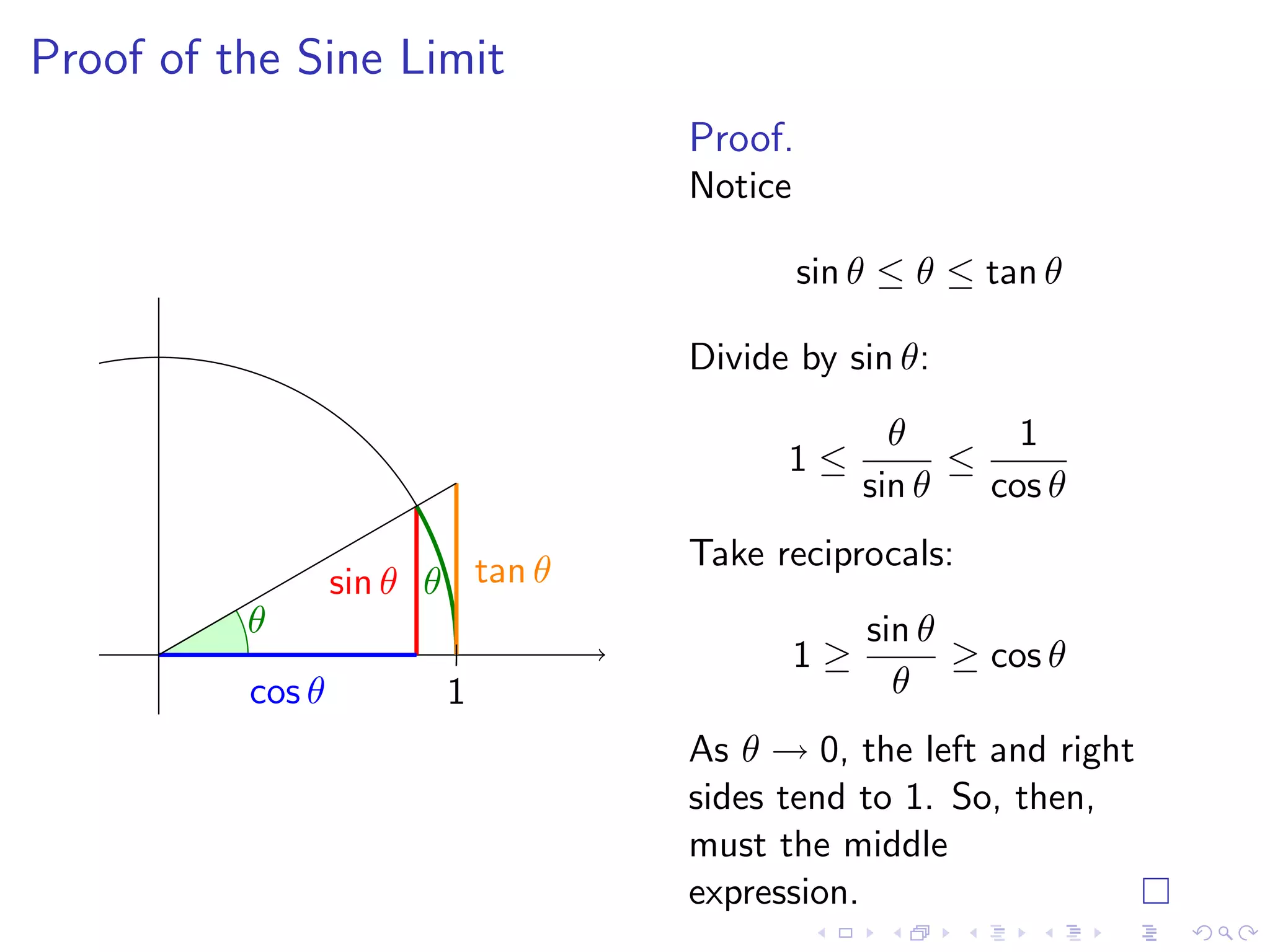
Details on limits of sinθ/θ and (cosθ - 1)/θ as θ approaches 0, including proofs.
Proof of the derivative of sine function, showing d(sin x)/dx = cos x using definition.
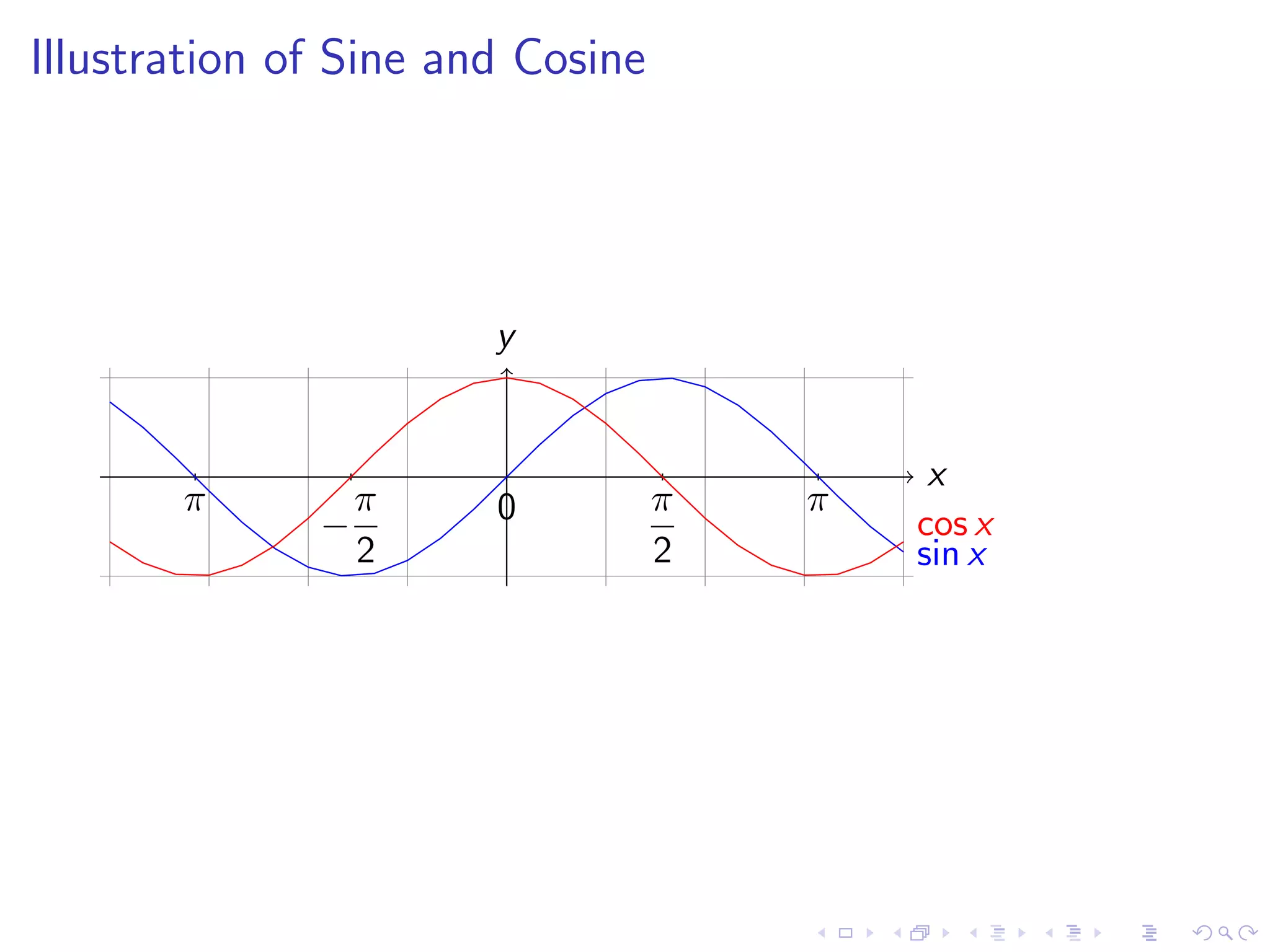
Further elucidation of the derivative of sine and cosine, along with graphical illustration.
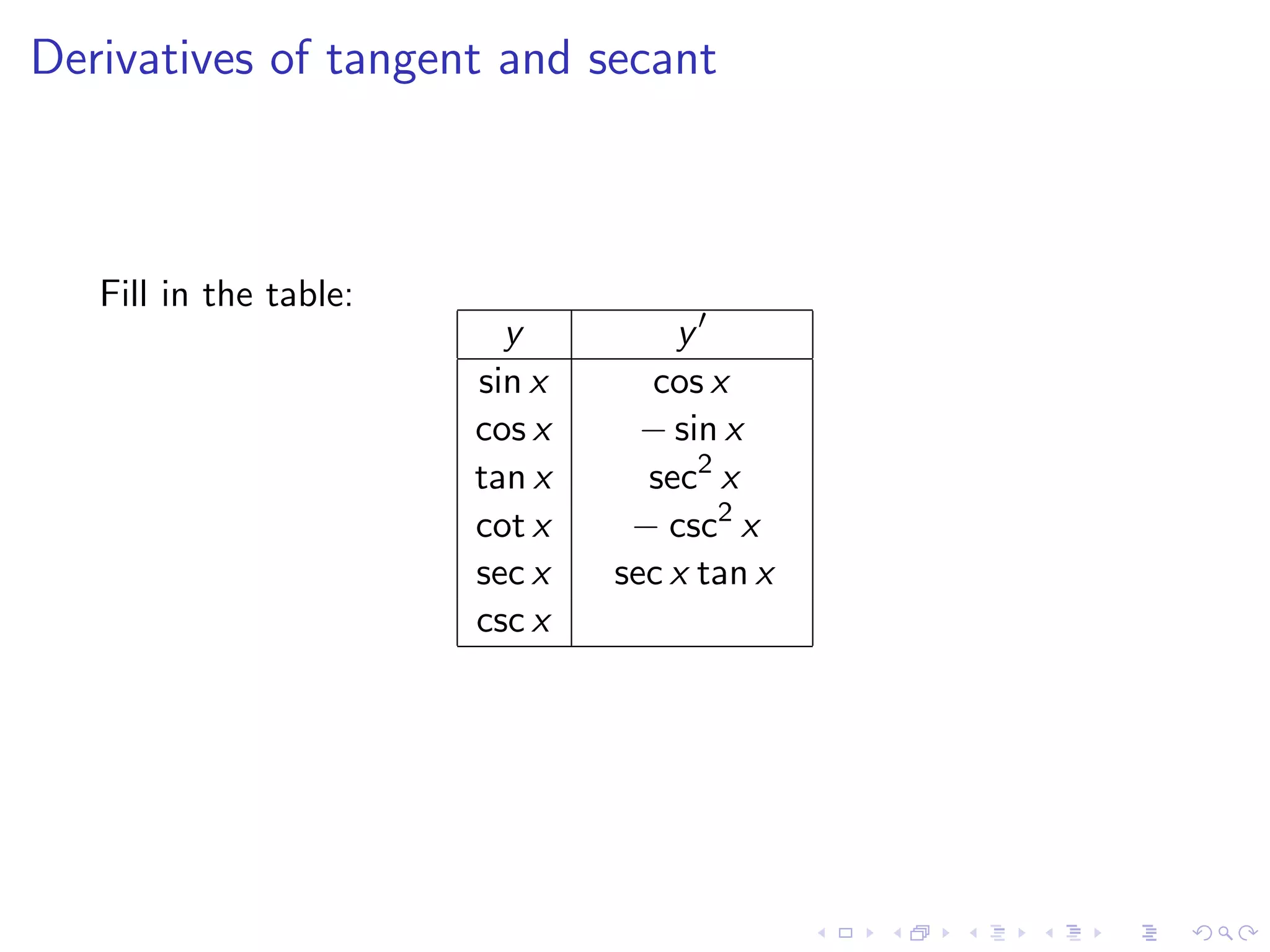
Introduction to the derivatives of tangent, cotangent, secant, and cosecant, with a fill-in-the-table example.
Application of limits and changes of variables in evaluating sin(2θ)/θ as θ approaches 0.