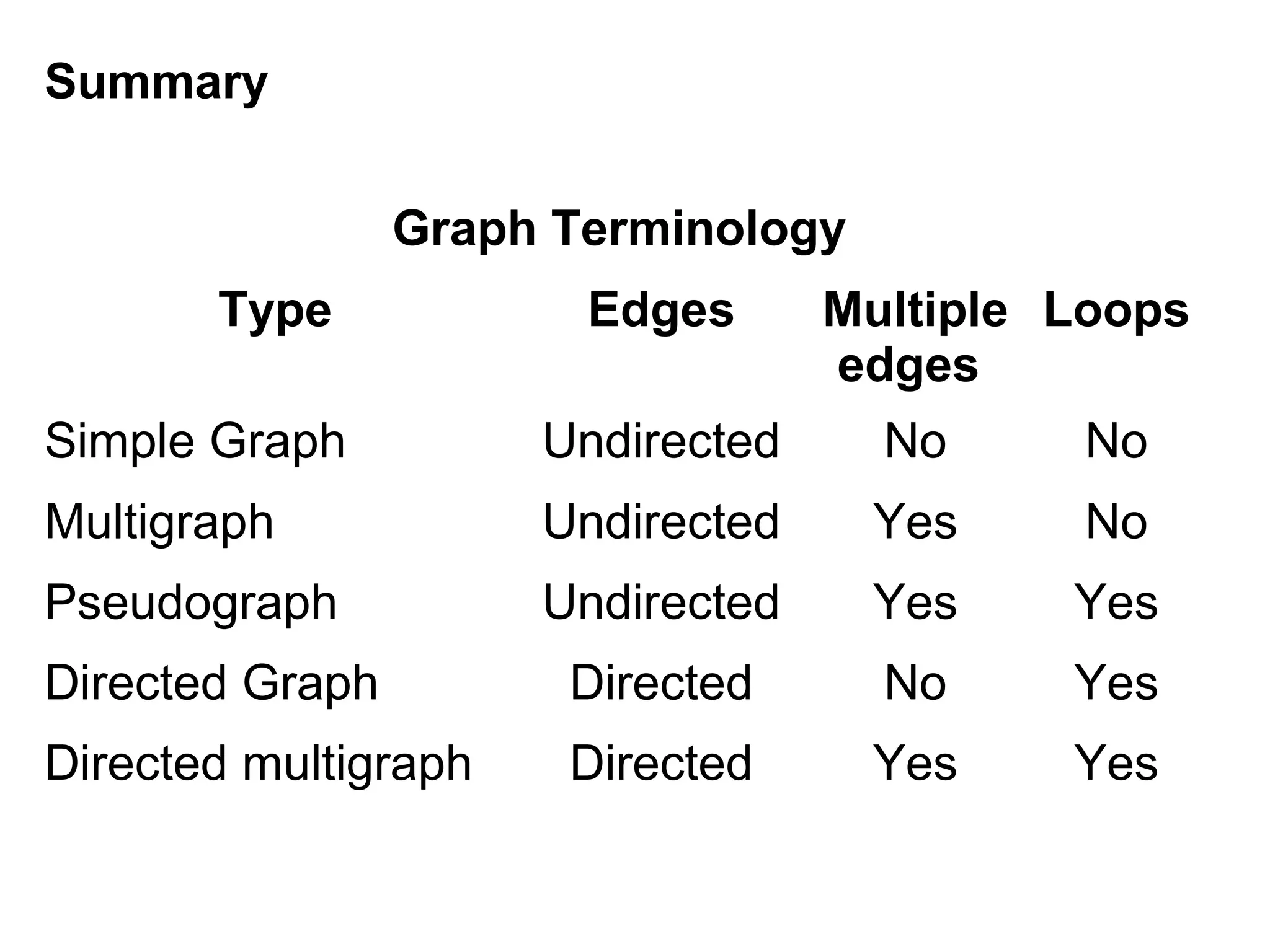
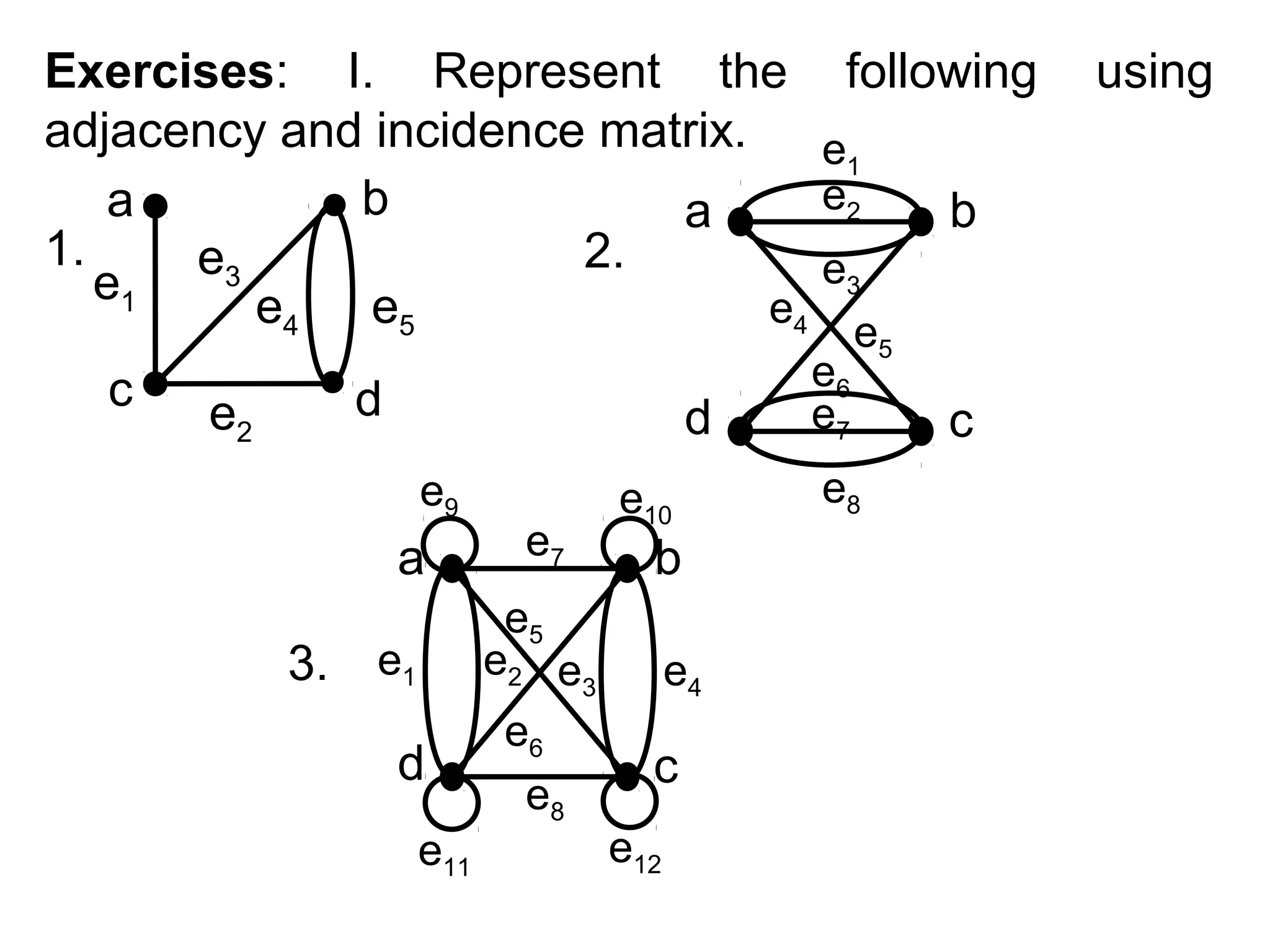
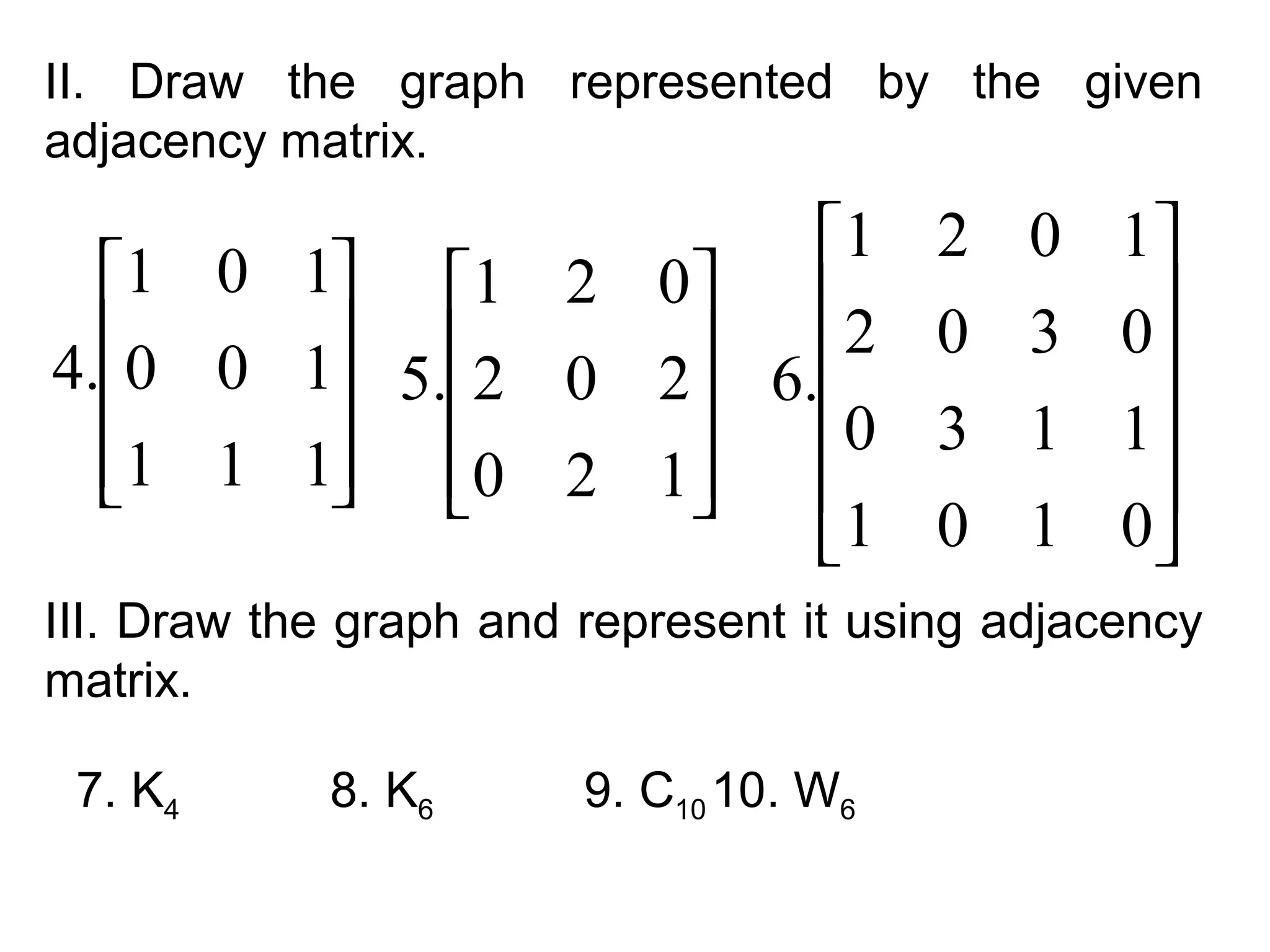
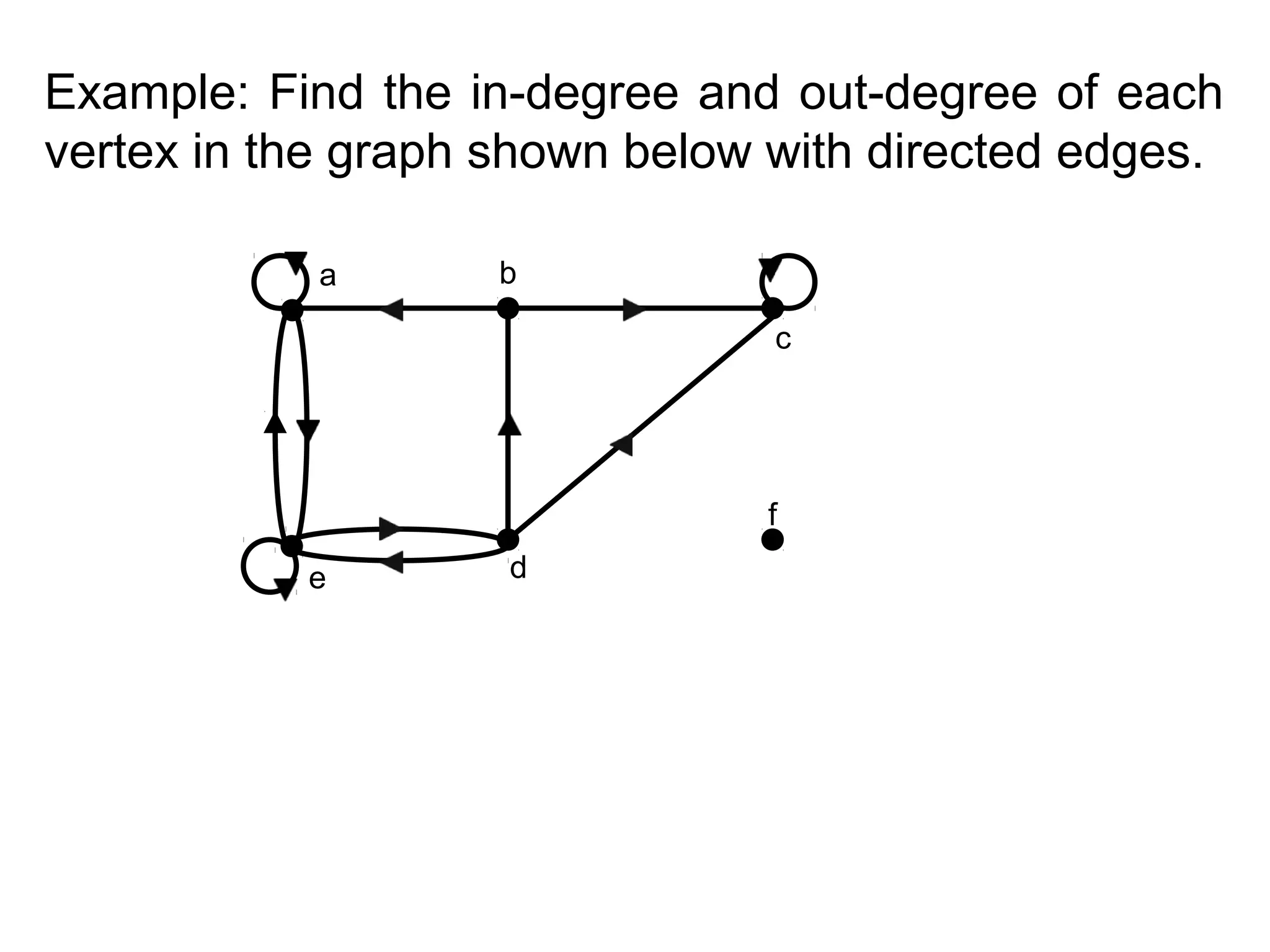
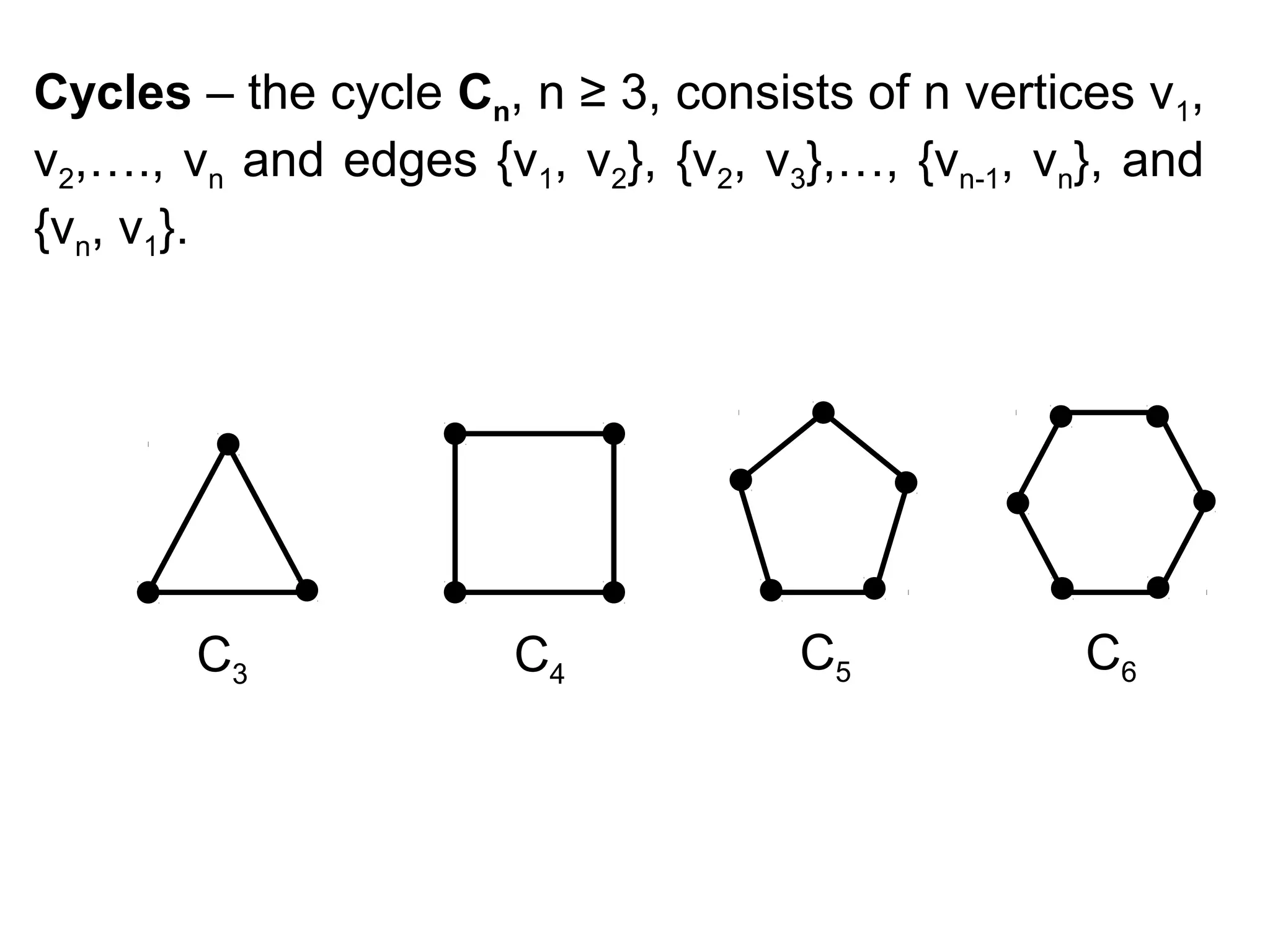
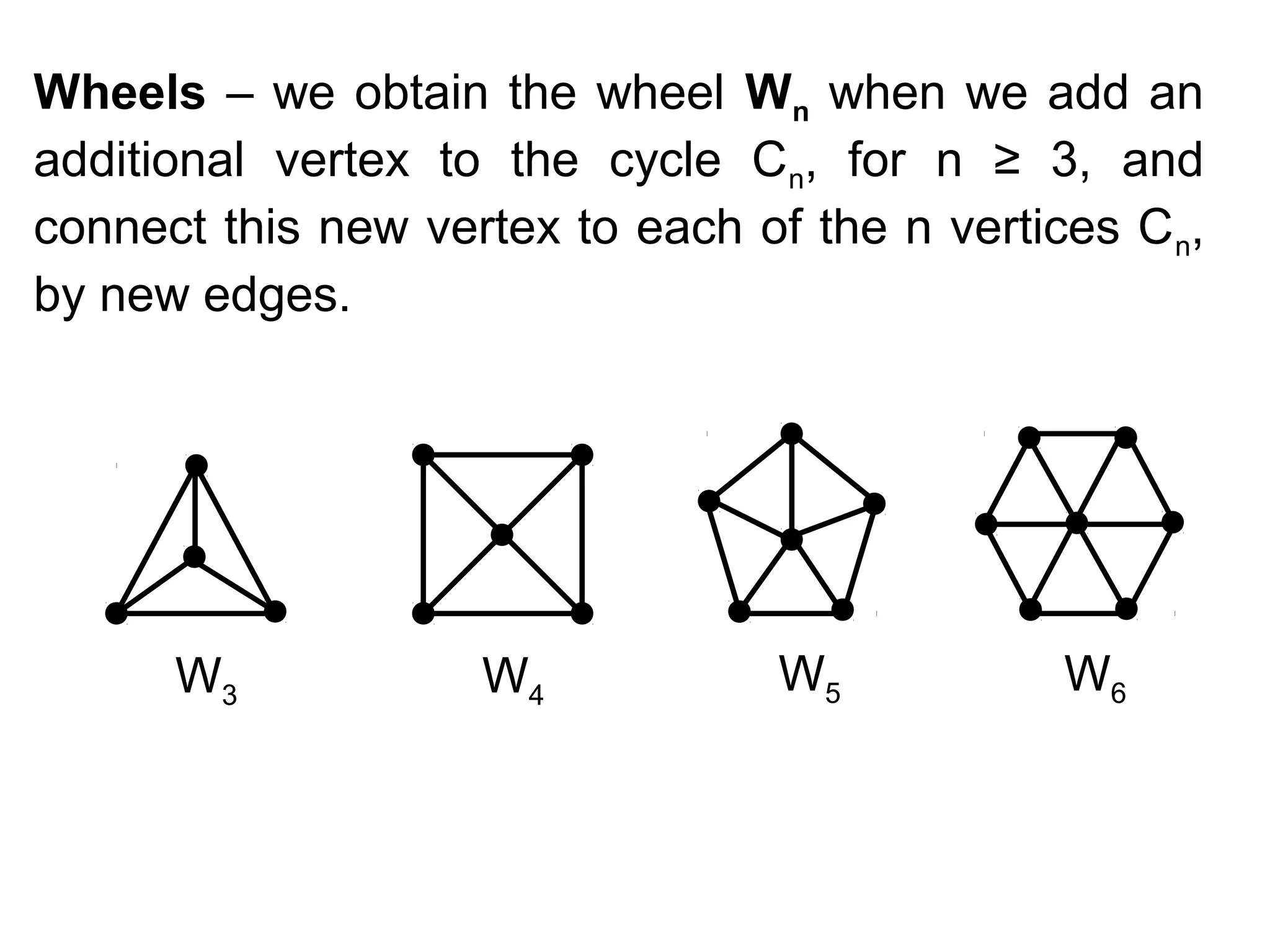
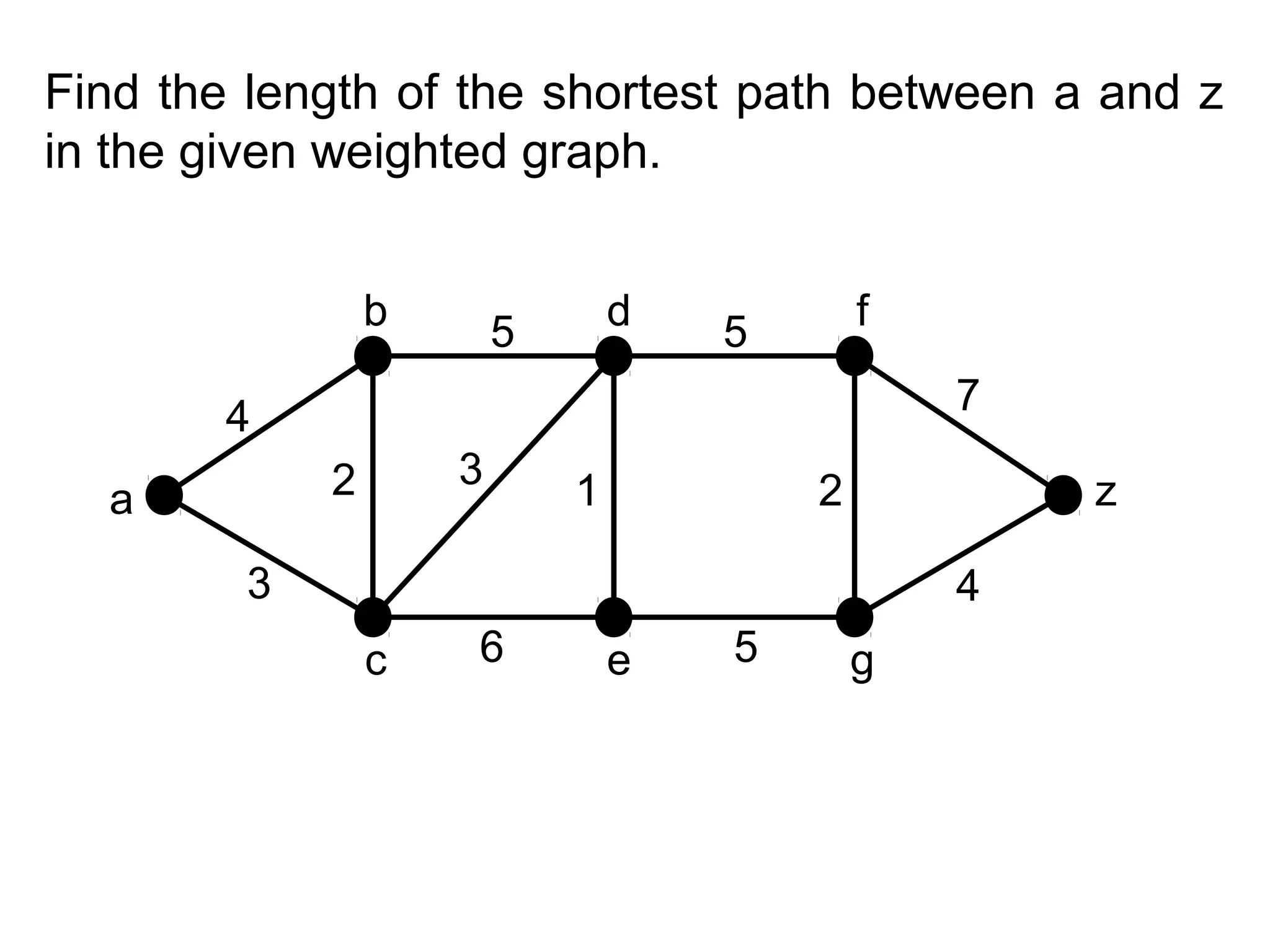
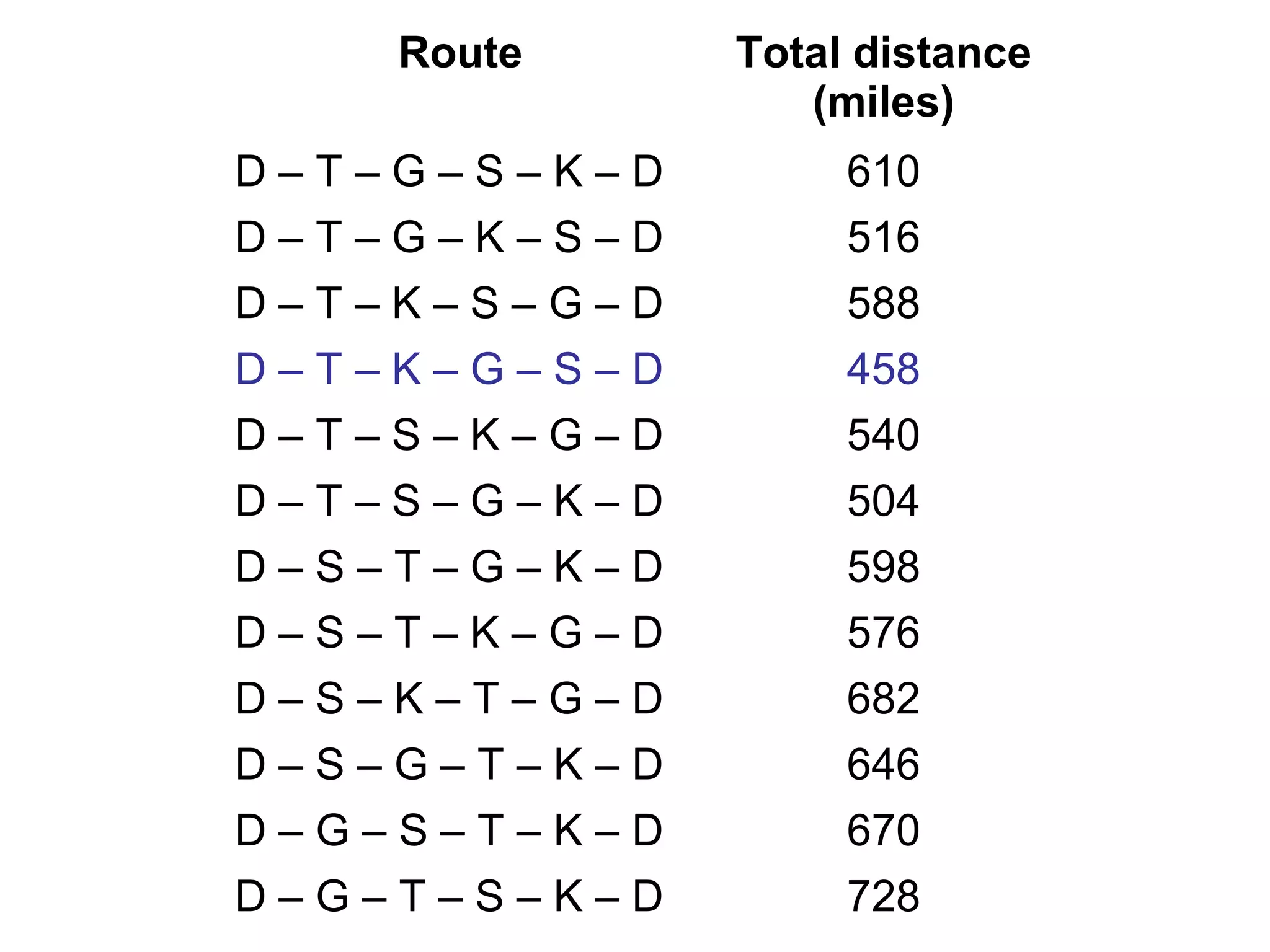
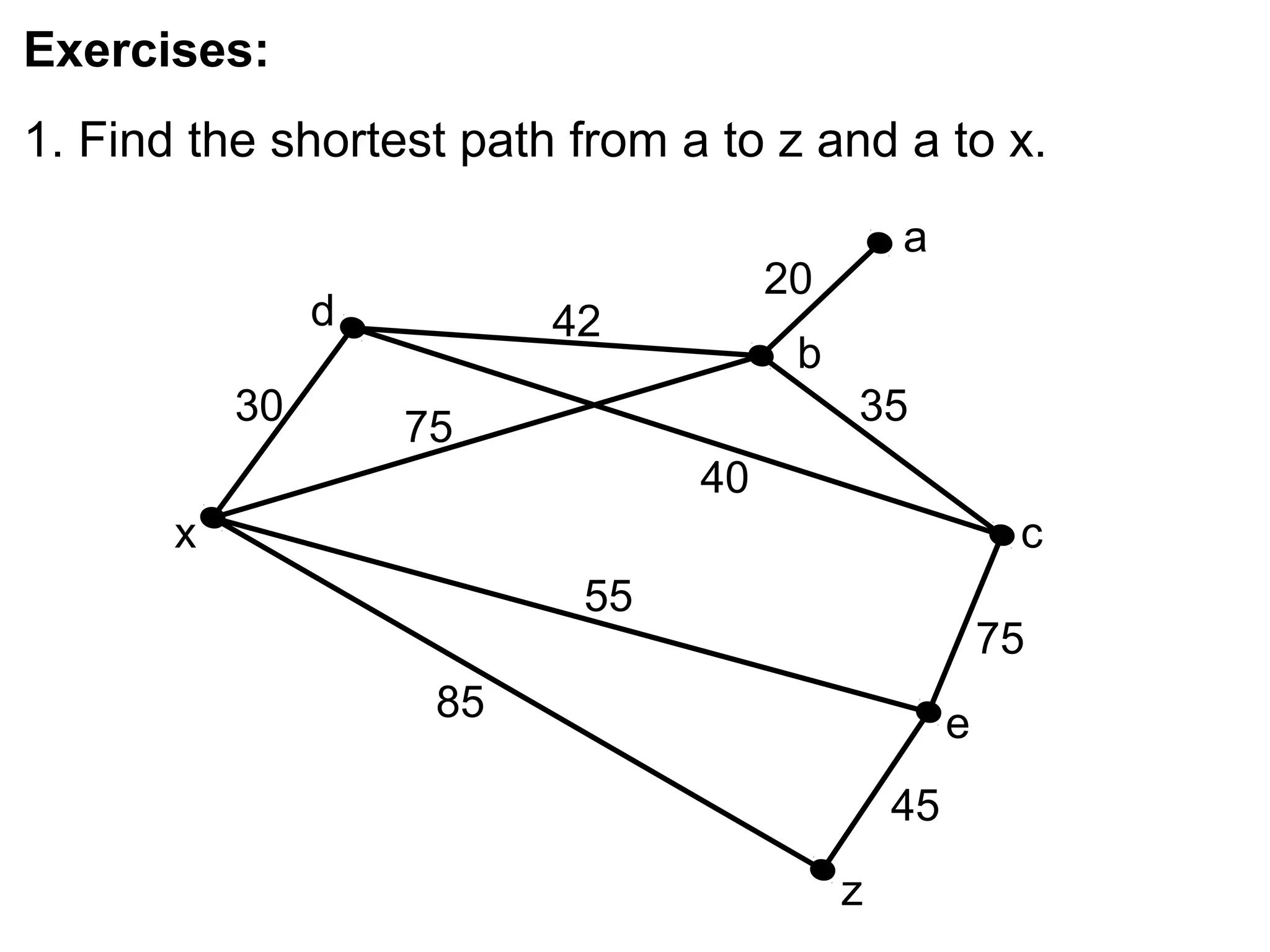
The document discusses various graph theory concepts including: - Types of graphs such as simple graphs, multigraphs, pseudographs, directed graphs, and directed multigraphs which differ based on allowed edge connections. - Graph terminology including vertices, edges, degrees, adjacency, incidence, paths, cycles, and representations using adjacency lists and matrices. - Weighted graphs and algorithms for finding shortest paths such as Dijkstra's algorithm. - Euler and Hamilton paths/circuits and conditions for their existence. 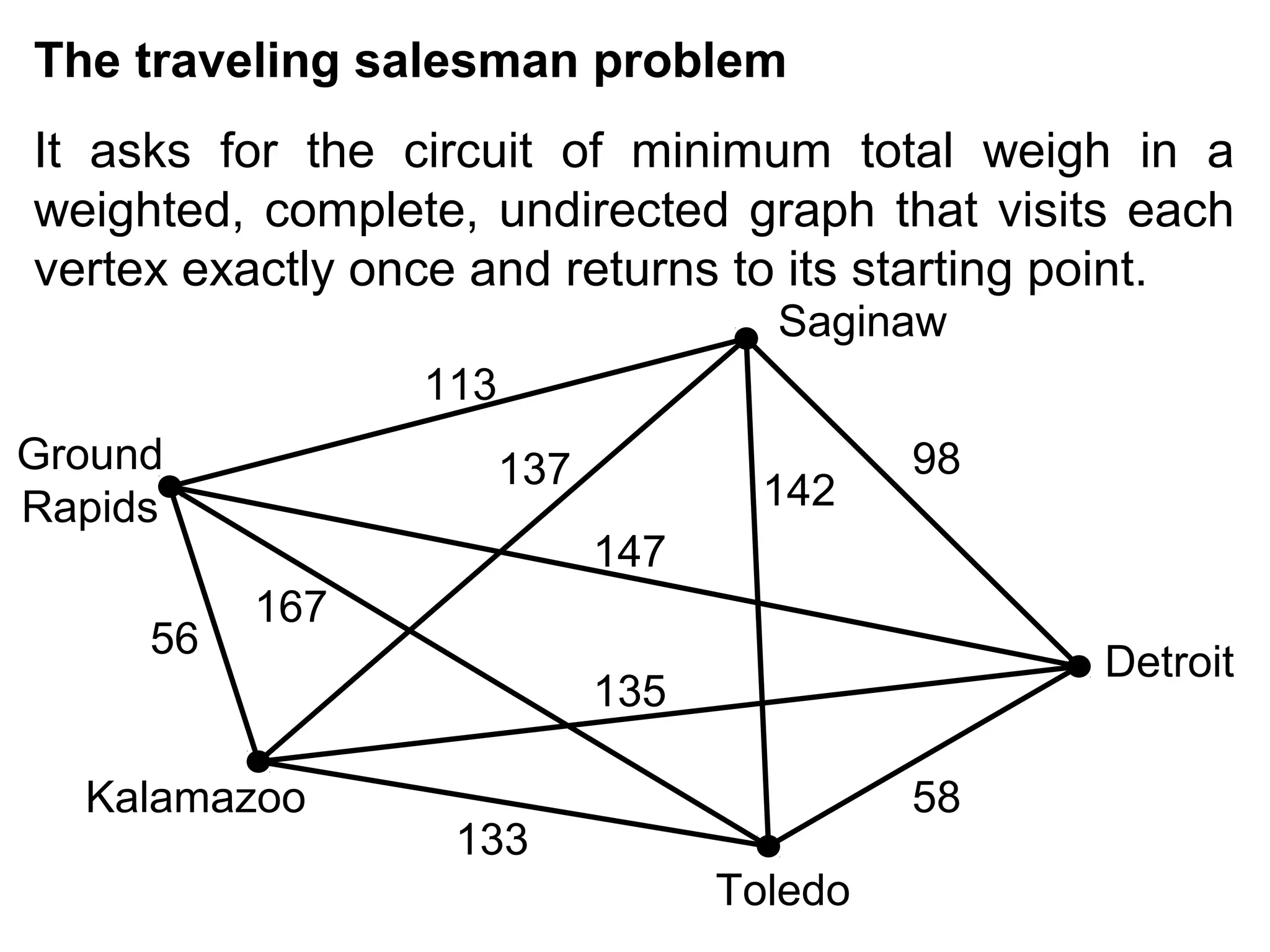- The traveling salesman problem of finding the shortest circuit visiting all vertices.

1. Graph Theory
Graphs are discrete structures consisting of vertices
and edges that connects these vertices. There are
several types of graphs that differ with respect to the
kind and number of edges that can connect a pair of
vertices.
A simple graph G = (V, E) consists of V, a nonempty
set of vertices, and E, a set of unordered pairs of
distinct elements V called edges.
A multigraph G = (V, E) consists of a set V of
vertices, a set of E of edges, and a function f from E to
{{u, v} | u, v є V, u ≠ v}. The edges e1 and e2 are called
multiple or parallel edges if f(e1) = f(e2).

2. A pseudograph G = (V, E) consists of a set V of
vertices, a set E of edges, and a function f from E to
{{u, v} | u, v є V}. An edge is loop of f(e) = {u, u} = {u}
for some u є V.
A directed graph (V, E) consists of a set of vertices V
and a set of edges E that are ordered pairs of
elements V.
A directed multigraph G = (V, E) consists of a set of
vertices V and a set of edges E, and d function f from
E to {(u, v) | u, v ε V}. The edges e1 and e2 are multiple
edges if f(e1) = f(e2).

3. Summary
Graph Terminology
Type
Edges
Multiple Loops
edges
Simple Graph
Undirected
No
No
Multigraph
Undirected
Yes
No
Pseudograph
Undirected
Yes
Yes
Directed Graph
Directed
No
Yes
Directed multigraph
Directed
Yes
Yes

4. Basic Terminology
Two vertices u and v in an undirected graph G are
called adjacent (or neighbors) in G if {u, v} is an
edge of G. If e = {u, v}, the edge e is called incident
with the vertices u and v. The edge e is also said to
connect u and v. The vertices u and v are called
endpoints of the edge {u, v}
The degree of a vertex in an undirected graph is the
number of edges incident with it, except that a loop at
a vertex contributes twice to the degree of that
vertex. The degree of the vertex v is denoted by
deg(v).
A vertex of degree 0 is called isolated.
A vertex is pendant if and only if it has degree 1.

5. Example: What are the degrees of the vertices in
graphs G and H.
b
G
a
c
b
H
e
g
e
f
a
d
d
c

6. Theorem 1
The Handshaking Theorem Let G = (V, E) be an
undirected graph with e edges. Then
2e = ∑ deg( v )
vεV
Example: How many edges are there in a graph with
10 vertices each of degree 6.
2e = (10)(6)
2e = 60
e = 30

7. Theorem 2
An undirected graph has an even number of vertices
of odd degree.
When (u, v) is an edge of the graph G with directed
edges, u is said to adjacent to u and v is said to be
adjacent from u. The vertex u is called the initial
vertex of (u, v), and v is called the terminal or end
vertex of (u, v). The initial vertex and terminal vertex
of a loop are the same.

8. In a graph with directed edges the in-degree of a
vertex v, denoted by deg – (v), is the number of edges
with v as their terminal vertex. The out-degree of v,
denoted by deg + (v), is the number of edges with v
as their initial vertex. (Note that a loop at a vertex
contributes 1 to both the in-degree and the outdegree of this vertex.)
Let G = (V, E) be a graph with directed edges. Then
−
+
∑ deg ( v ) = ∑ deg ( v ) = E
vεV
vεV

9. Example: Find the in-degree and out-degree of each
vertex in the graph shown below with directed edges.
a
b
c
f
e
d

10. Cycles – the cycle Cn, n ≥ 3, consists of n vertices v1,
v2,…., vn and edges {v1, v2}, {v2, v3},…, {vn-1, vn}, and
{vn, v1}.
C3
C4
C5
C6

11. Wheels – we obtain the wheel Wn when we add an
additional vertex to the cycle Cn, for n ≥ 3, and
connect this new vertex to each of the n vertices C n,
by new edges.
W3
W4
W5
W6

12. Representing Graphs
Adjacency lists – is used to represent a graph with
no multiple edges which specify the vertices that are
adjacent to each vertex of the graph.
B
A
E
B
C
A
D
C
E
D
Vertex Adjacent
Vertices
Vertex Adjacent
Vertices
A
B
C
D
E
A
B
C
D
E
B, C, E
A
A, D, E
C, E
A, C, D
B, C, D, E
B, D
A, C, E
B, C, D

13. Adjacency matrix (Ag), with respect to this listing of
the vertices, is the n x n zero-one matrix with 1 as its
(i, j)th entry when vi and vj are adjacent, and 0 as its
(i, j) entry when they are not adjacent. In other words,
if its adjacency matrix is A = [aij], then
1
aij = 
0
a
c
If {vi, vj} is an edge of G,
otherwise.
0
b 
1

1
d 
1
1
0
1
0
1
1
0
0
1

0
0

0
a
d
0
b
1

1
c
0
1
0
0
1
1
0
0
1
0

1
1

0

14. Adjacency matrices can also be used to represent
undirected graphs with loops and with multiple
edges. A loop at the vertex ai is represented by 1 at
the (i, j)th position of the adjacency matrix. When
multiple edges are present, the adjacency matrix is
no longer zero-one matrix, since the (i, j) entry of this
matrix equals the number of edges that are
associated to {ai, aj}. All undirected graphs, including
multigraphs and pseudographs, have symmetric
adjacency matrices
0 3 0 2
a
b


d
c
3 0 0 1

0 0 1 2


2 1 2 0

15. Incidence matrices – Let G = (V, E) be an
undirected graph. Suppose that v1, v2, …, vn are the
vertices and e1, e2, …., em are the edges of G. Then
the incidence matrix with respect to this ordering of V
and E is the n x m matrix M = [mij], where
1
mij = 
0
v1
e1
v4
e3
e2
when edge ej is incident with vi,
otherwise.
v 2 e6
e4
v5
v3
e5
1
0

0

1
0

1 0 0 0 0

0 1 1 0 1
0 0 0 1 1

0 1 0 0 0
1 0 1 1 0


16. Exercises: I. Represent the following
adjacency and incidence matrix.
e1
e2
b
a
a
b
1.
2.
e3
e3
e1
e4
e4 e5
e
c
e2
d
d
e9
a
3. e1
d
e11
e7
e5
e2 e3
e6
e8
e10
b
e4
c
e12
e6
e7
e8
5
c
using

17. II. Draw the graph represented by the given
adjacency matrix.
1 0 1 1 2 0
0 0 1 

4.
 5.2 0 2
1 1 1 0 2 1 

 

1
2
6.
0

1
2 0 1

0 3 0
3 1 1

0 1 0
III. Draw the graph and represent it using adjacency
matrix.
7. K4
8. K6
9. C10 10. W6

18. Shortest Path Problems
Applications: mileage, flight times, fares, distance,
response time, least rates, and so on.
Weighted graphs are graphs that have a number
assigned to each edge.
The length of a path in a weighted graph is the sum
of the weights of the edges of this path.

19. Dijktra’s Algorithm (a shortest path algorithm)
Theorem 1
Dijktra’s algorithm finds the length of a shortest path
between two vertices in a connected simple undirected
weighted graph.
Theorem 2
Dijktra’s algorithm uses O(n2) operations (additions
and comparisons) to find the length of the shortest
path between two vertices in a connected simple
undirected weighted graph.

20. Find the length of the shortest path between a and z
in the given weighted graph.
b
d
5
f
5
7
4
3
2
a
1
2
z
3
4
c
6
e
5
g

21. The traveling salesman problem
It asks for the circuit of minimum total weigh in a
weighted, complete, undirected graph that visits each
vertex exactly once and returns to its starting point.
Saginaw
113
Ground
Rapids
56
137
142
98
147
167
Detroit
135
Kalamazoo
58
133
Toledo

22. Route
Total distance
(miles)
D–T–G–S–K–D
D–T–G–K–S–D
D–T–K–S–G–D
D–T–K–G–S–D
D–T–S–K–G–D
D–T–S–G–K–D
D–S–T–G–K–D
D–S–T–K–G–D
D–S–K–T–G–D
D–S–G–T–K–D
D–G–S–T–K–D
D–G–T–S–K–D
610
516
588
458
540
504
598
576
682
646
670
728

23. Euler and Hamilton Paths
An Euler circuit in a graph G is s simple circuit
containing every edge of G. An Euler path in G is a
simple path containing every edge of G.
Theorem 1
A connected multigraph has an Euler circuit if and only
if each of its vertices has even degree.
Theorem 2
A connected multigraph has an Euler path but not
Euler circuit if and only if it has exactly two vertices of
odd degree.

24. A path x0, x1, …., xn-1, xn in the graph G = (V, E) is
called a Hamilton path if V = {x0, x1, …, xn-1, xn} and xi
≠ xj for 0 ≤ i , j ≤ n. A circuit x0, x1, …, xn-1, x0 (with n >
1) in a graph G = (V, E) is called Hamilton circuit if
x0, x1, …, xn-1, xn is a Hamilton path.
Theorem 3
If G is connected simple graph with n vertices where
n ≥ 3, then G has a Hamilton circuit if the degree of
each vertex is at least n/2.

25. Exercises:
1. Find the shortest path from a to z and a to x.
d
30
a
20
42
b
35
75
40
x
c
55
75
85
e
45
z

26. 2. Solve the traveling salesman problem for the
following graph by finding the total weight of all the
circuits and determining a circuit with minimum total
weight.
3
a
b
7
10
2
8
5
e
1
4
c
9
d
6