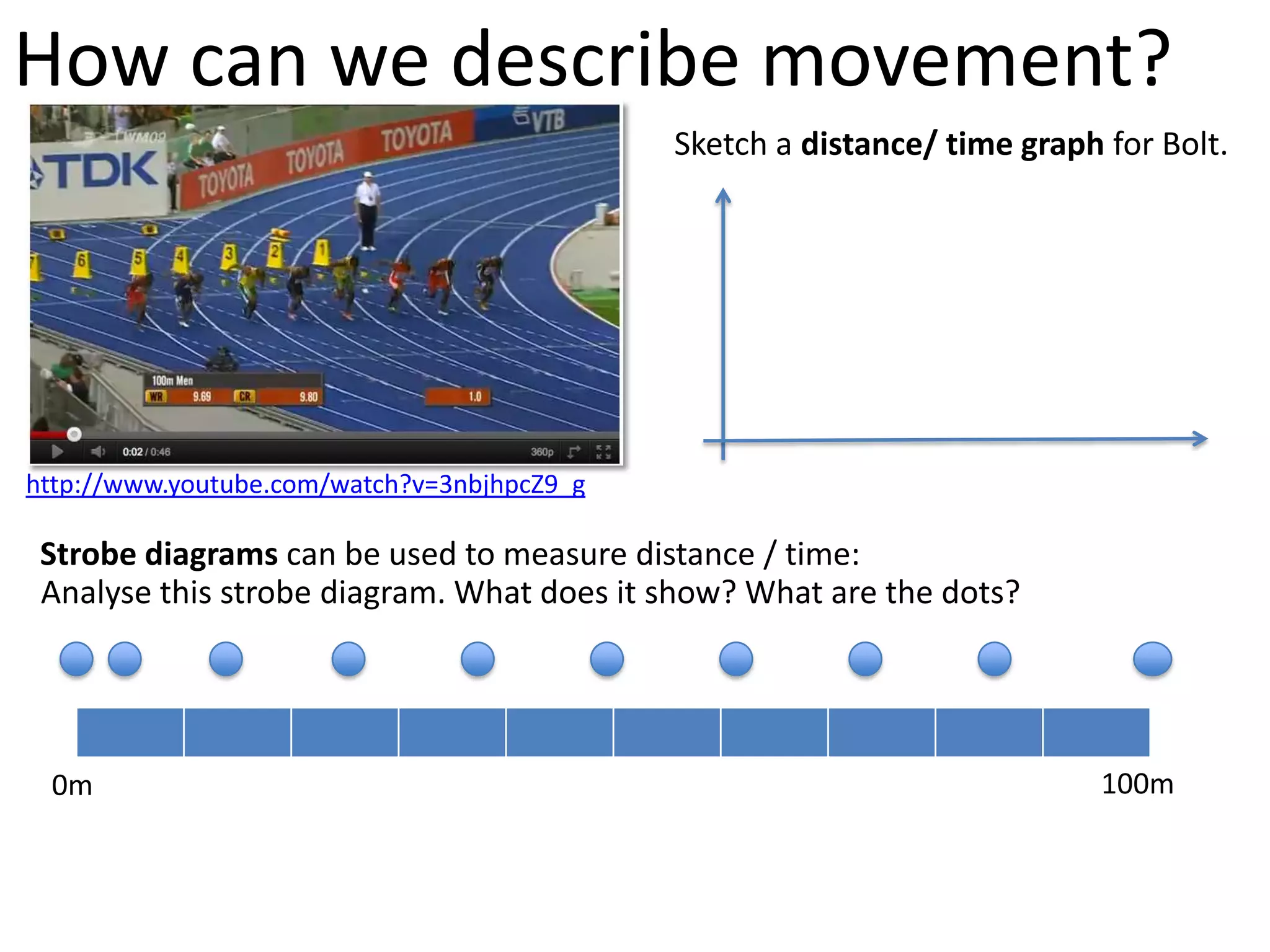
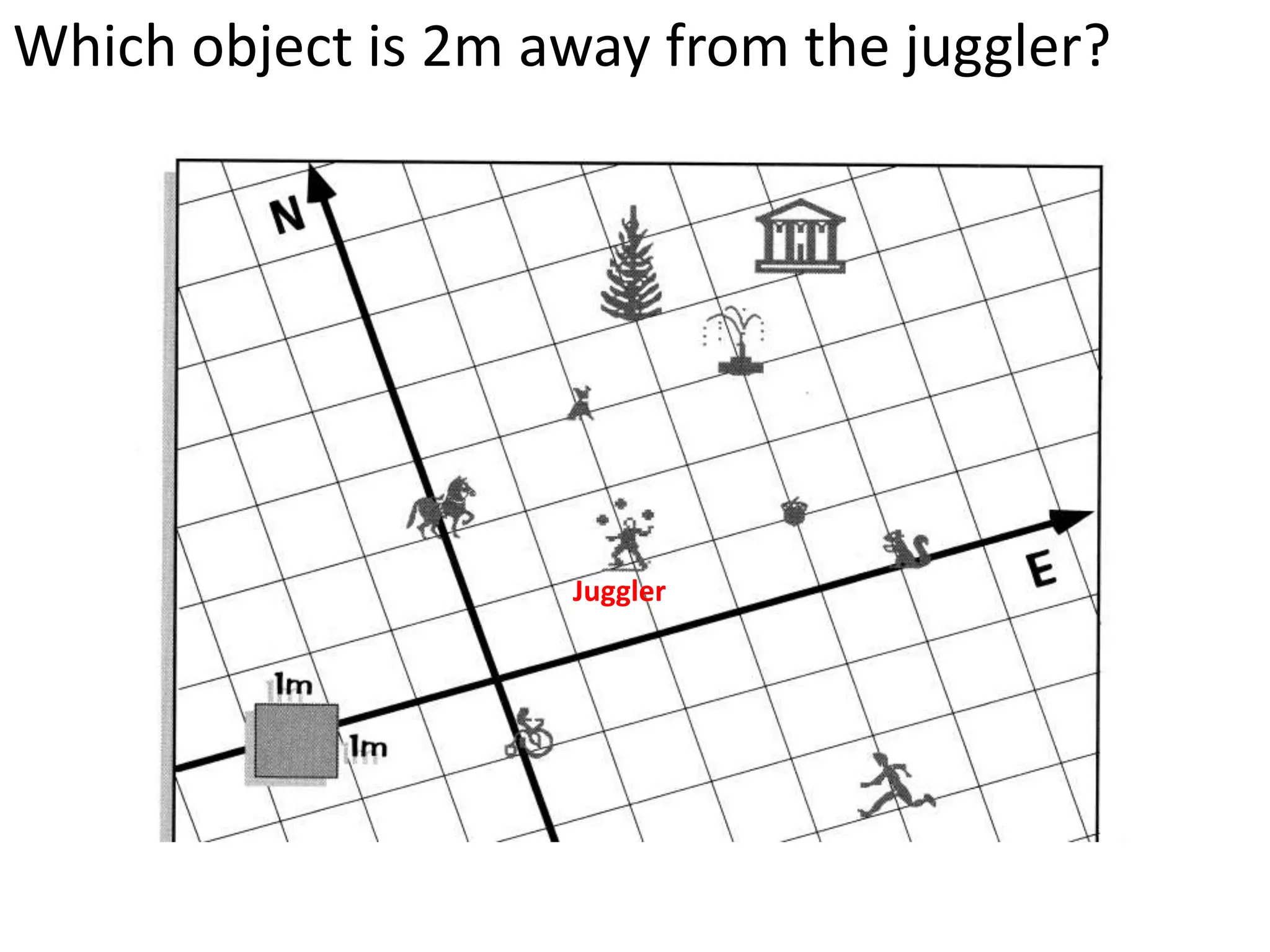
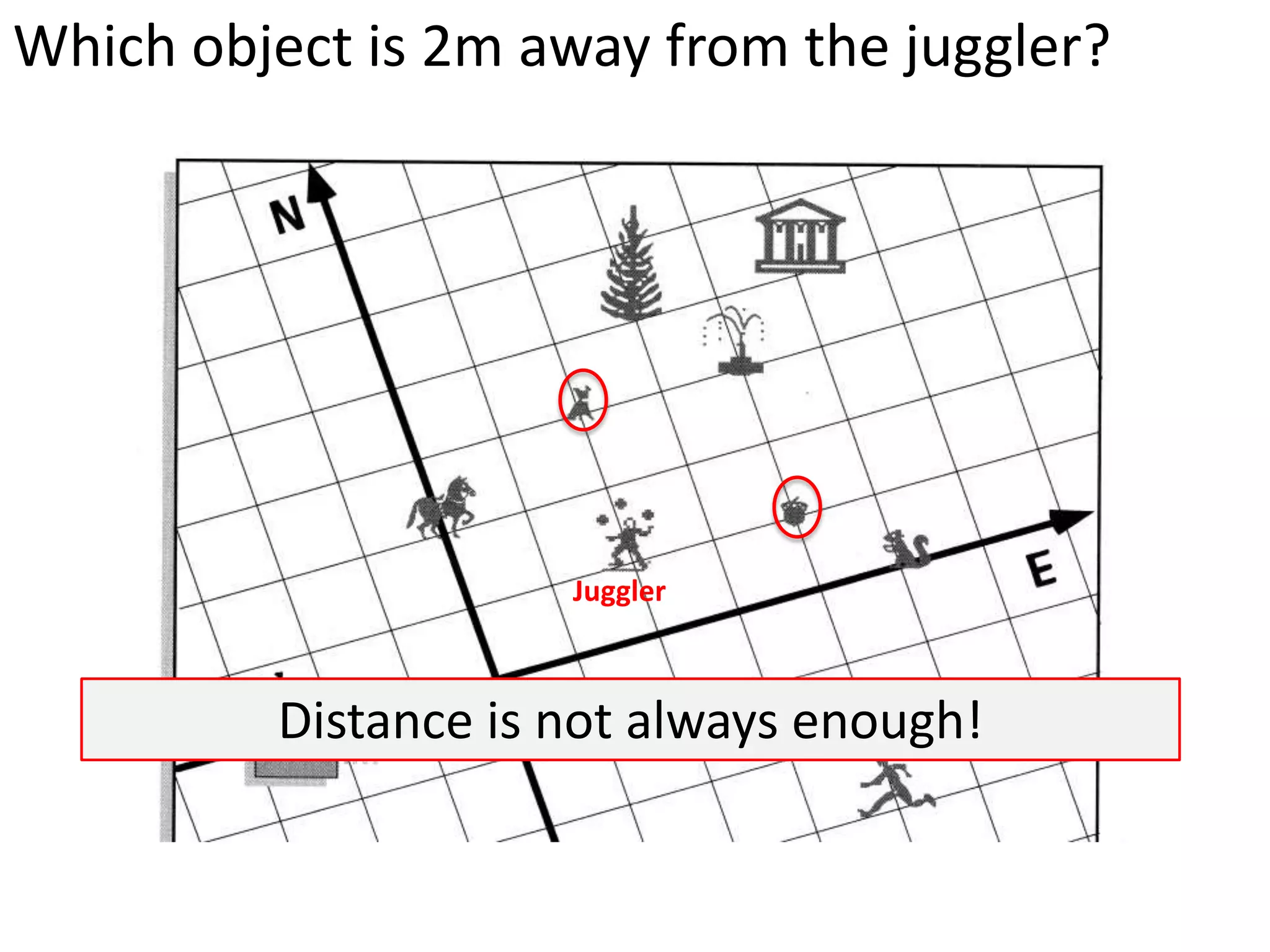
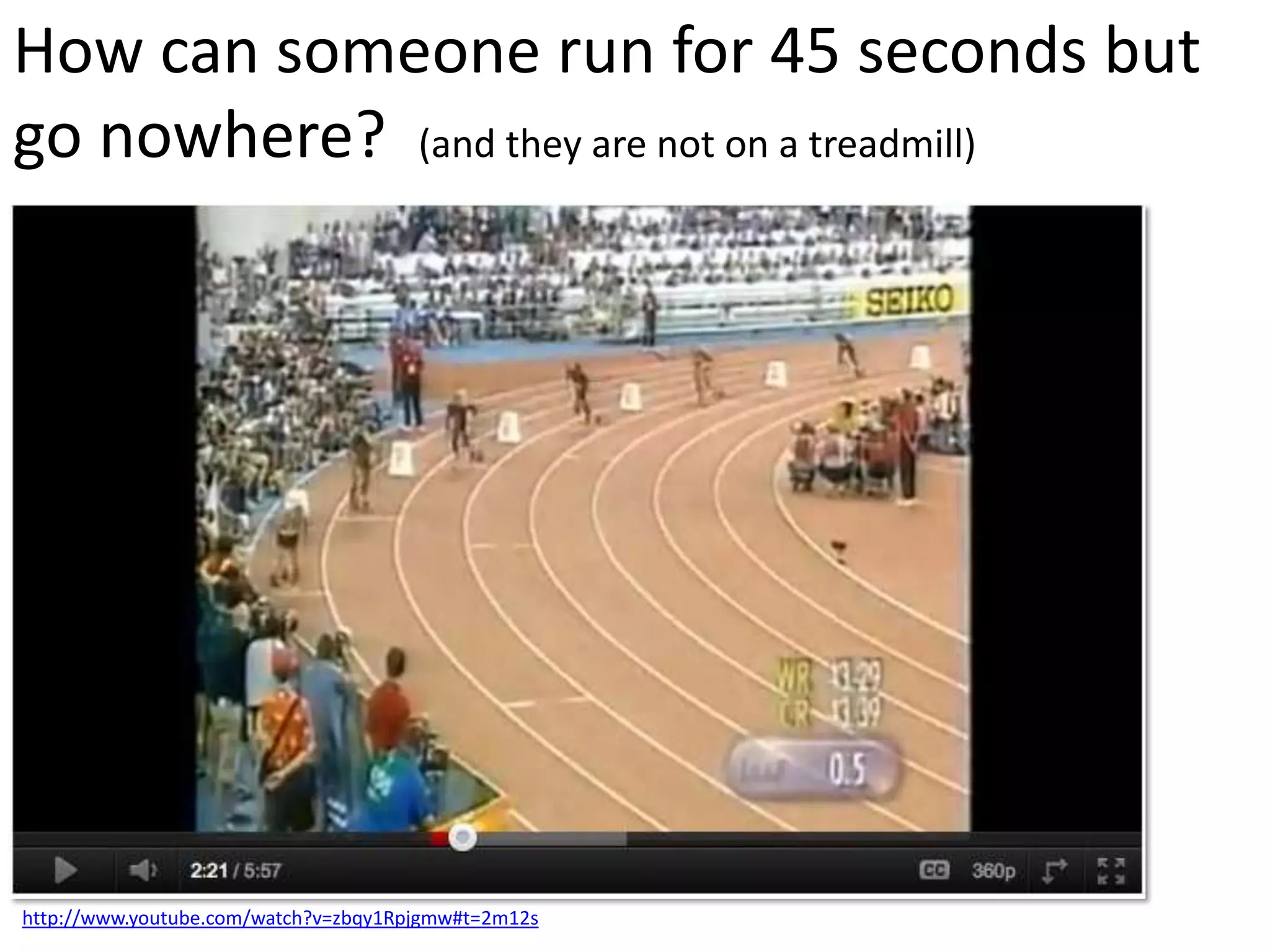
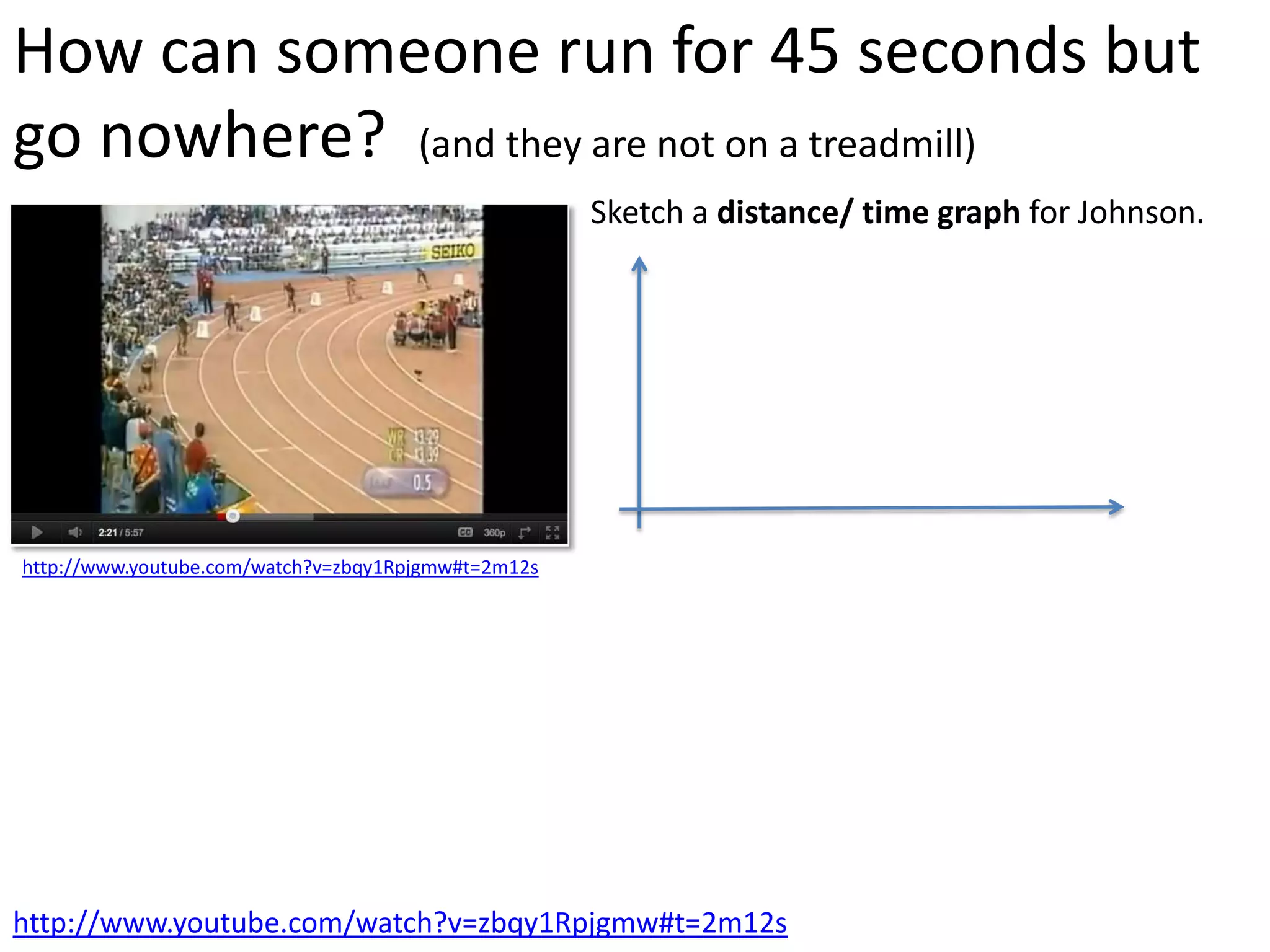
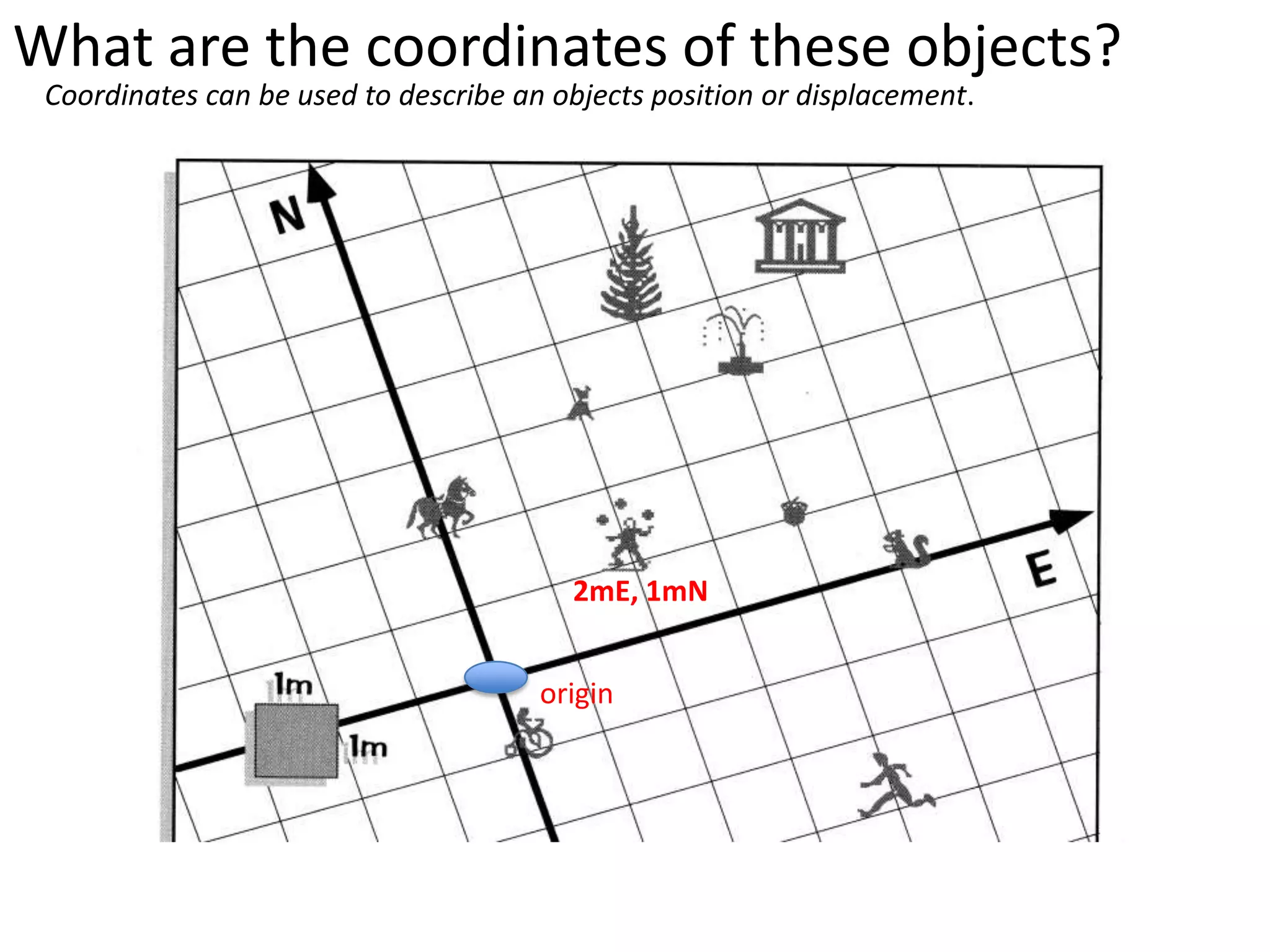
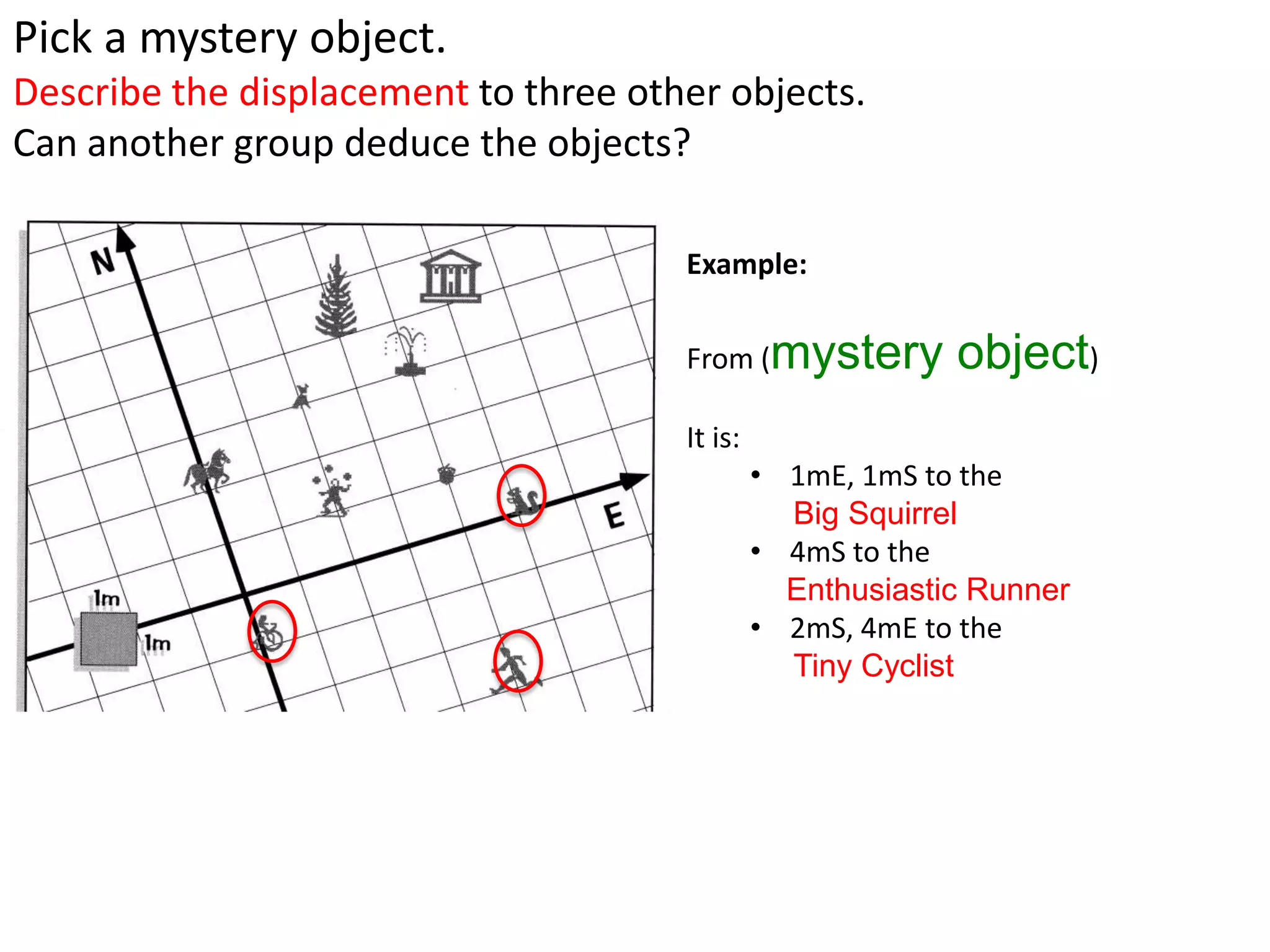
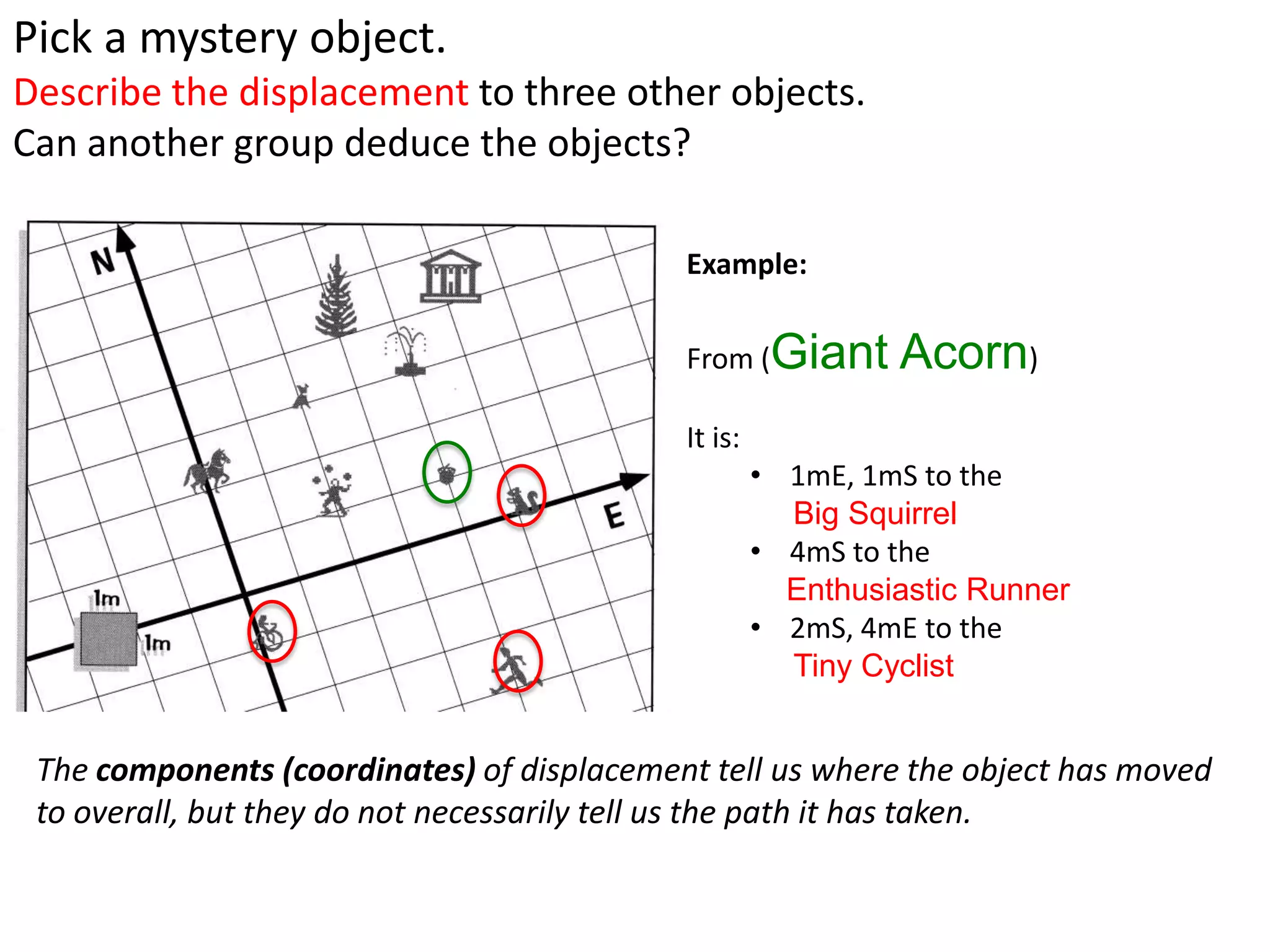
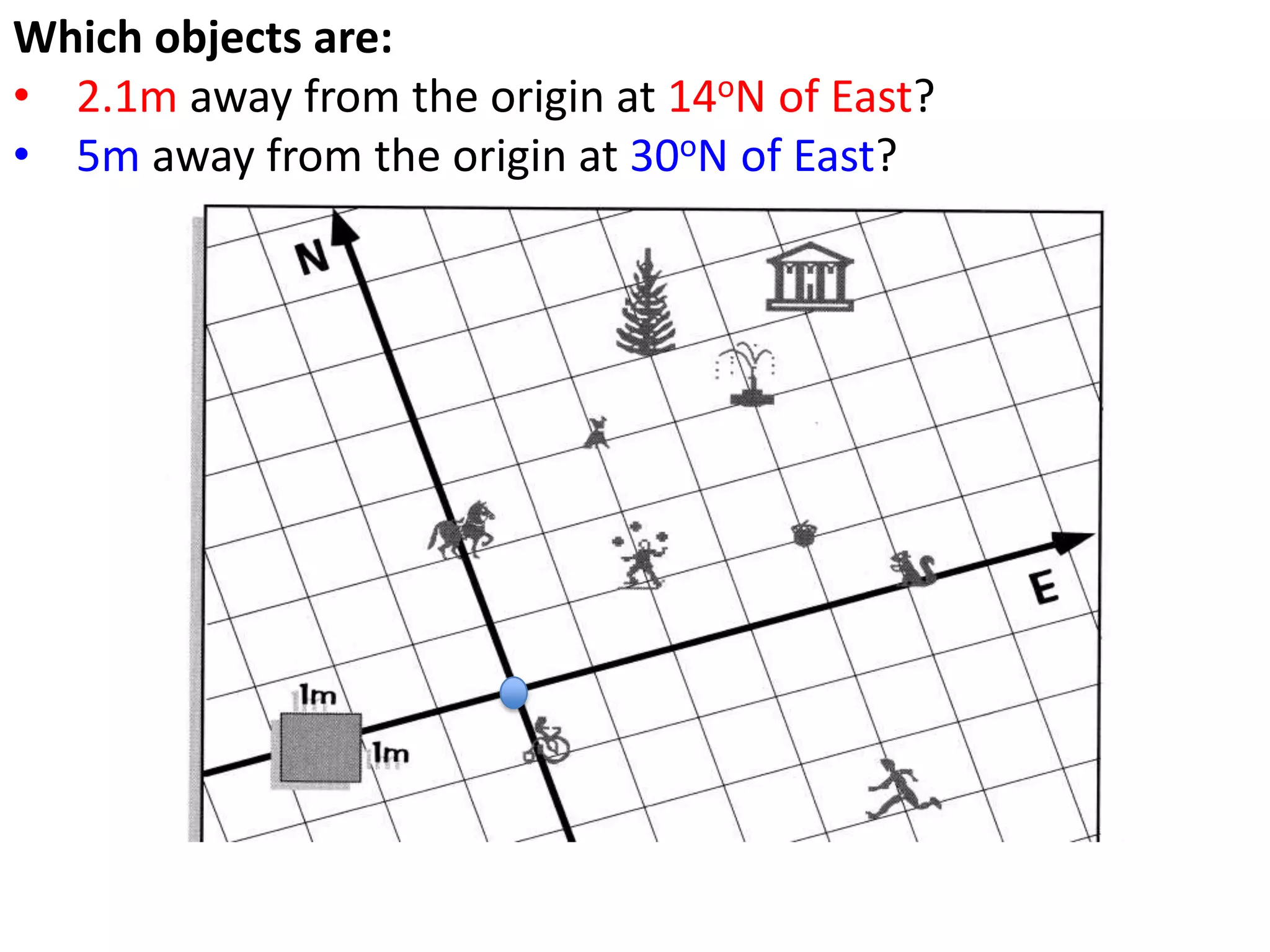
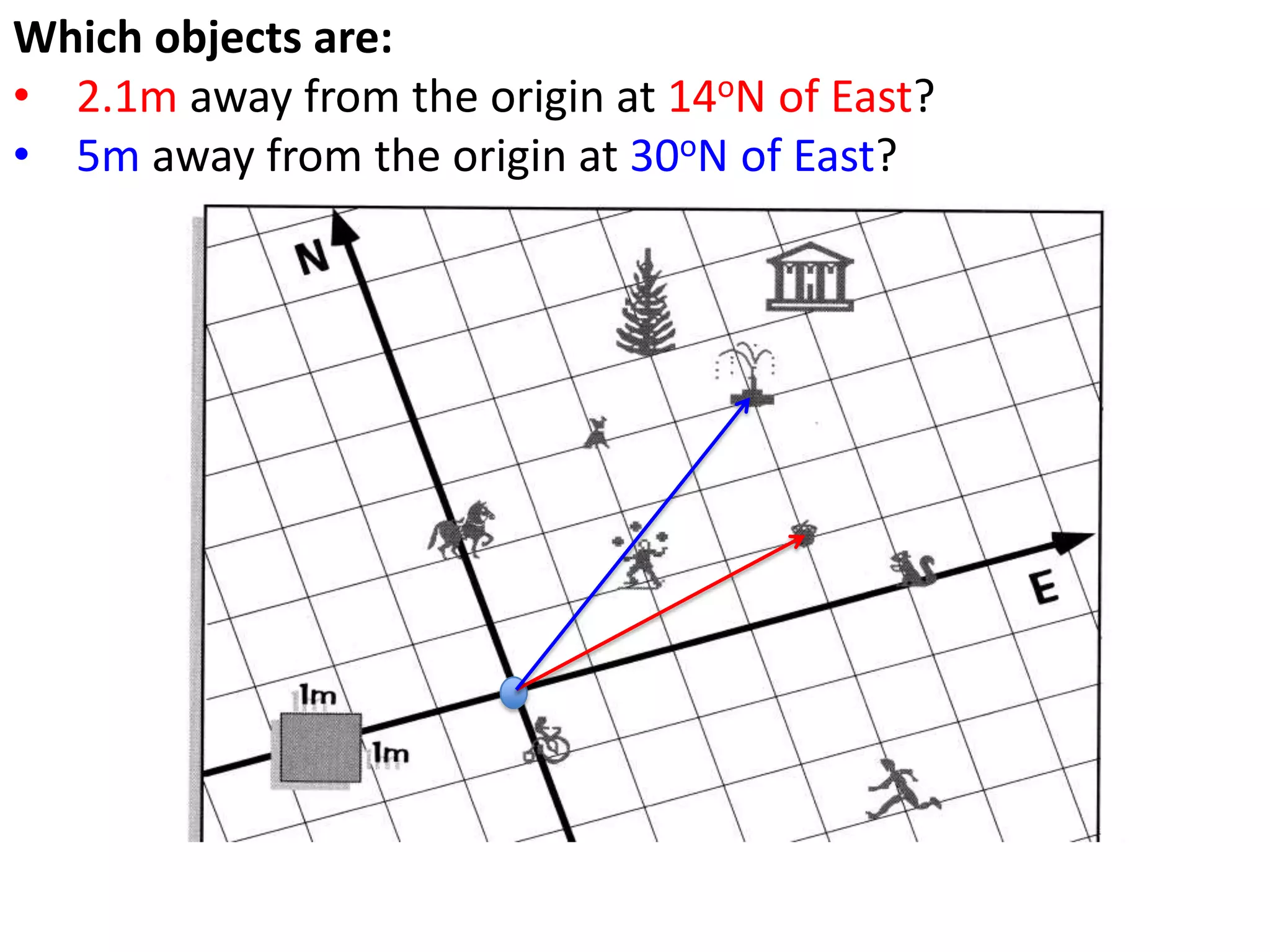
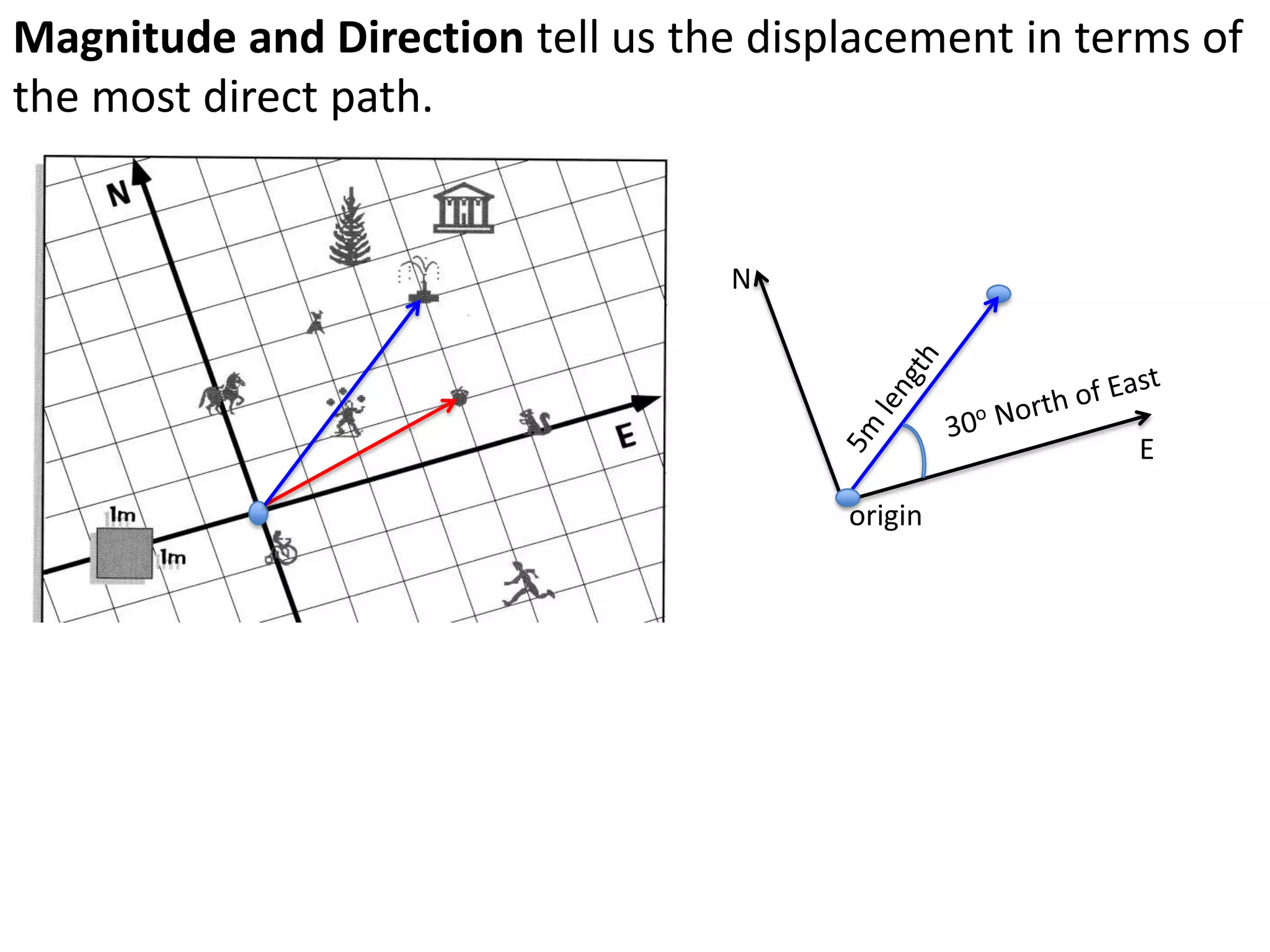
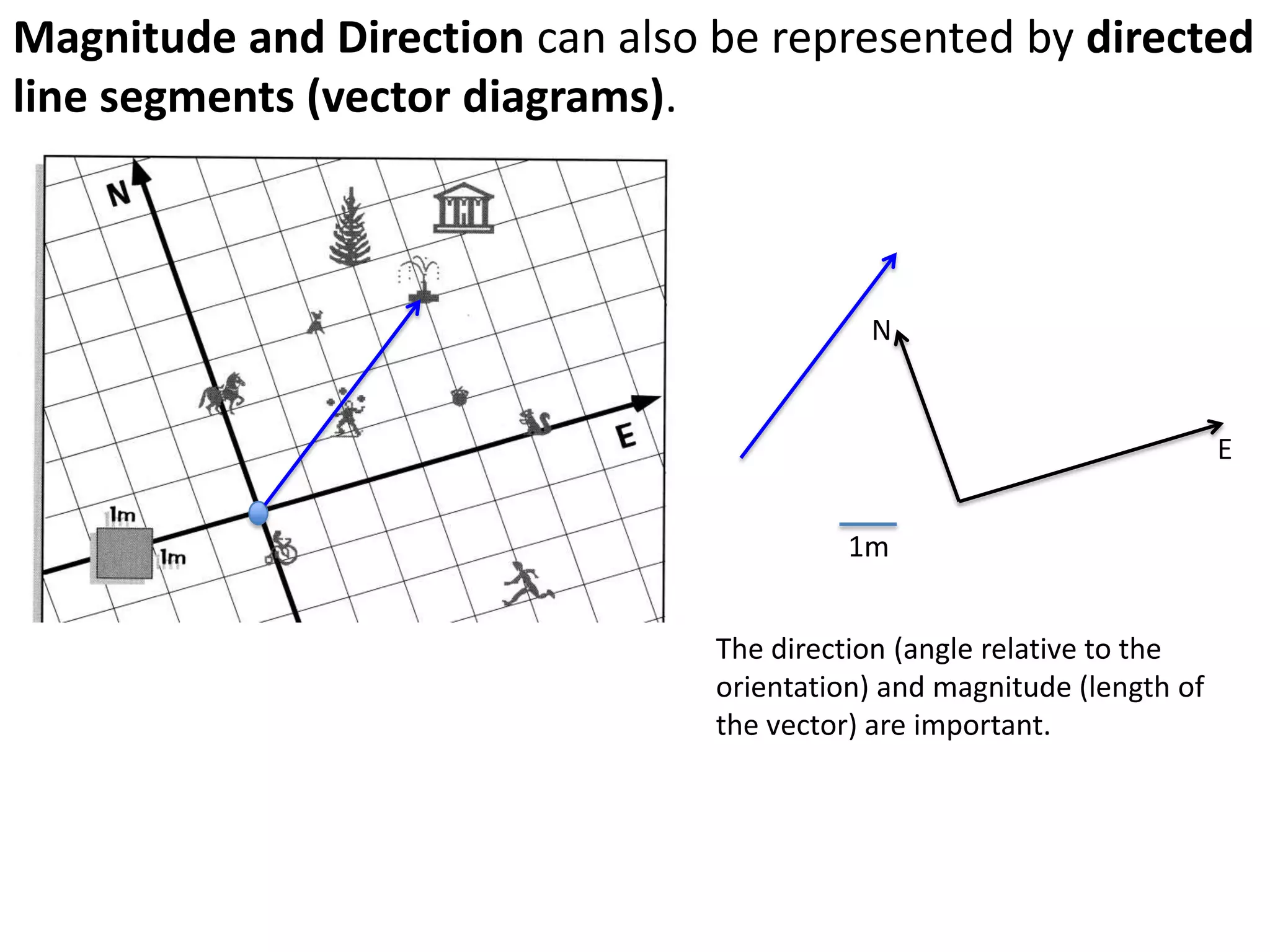
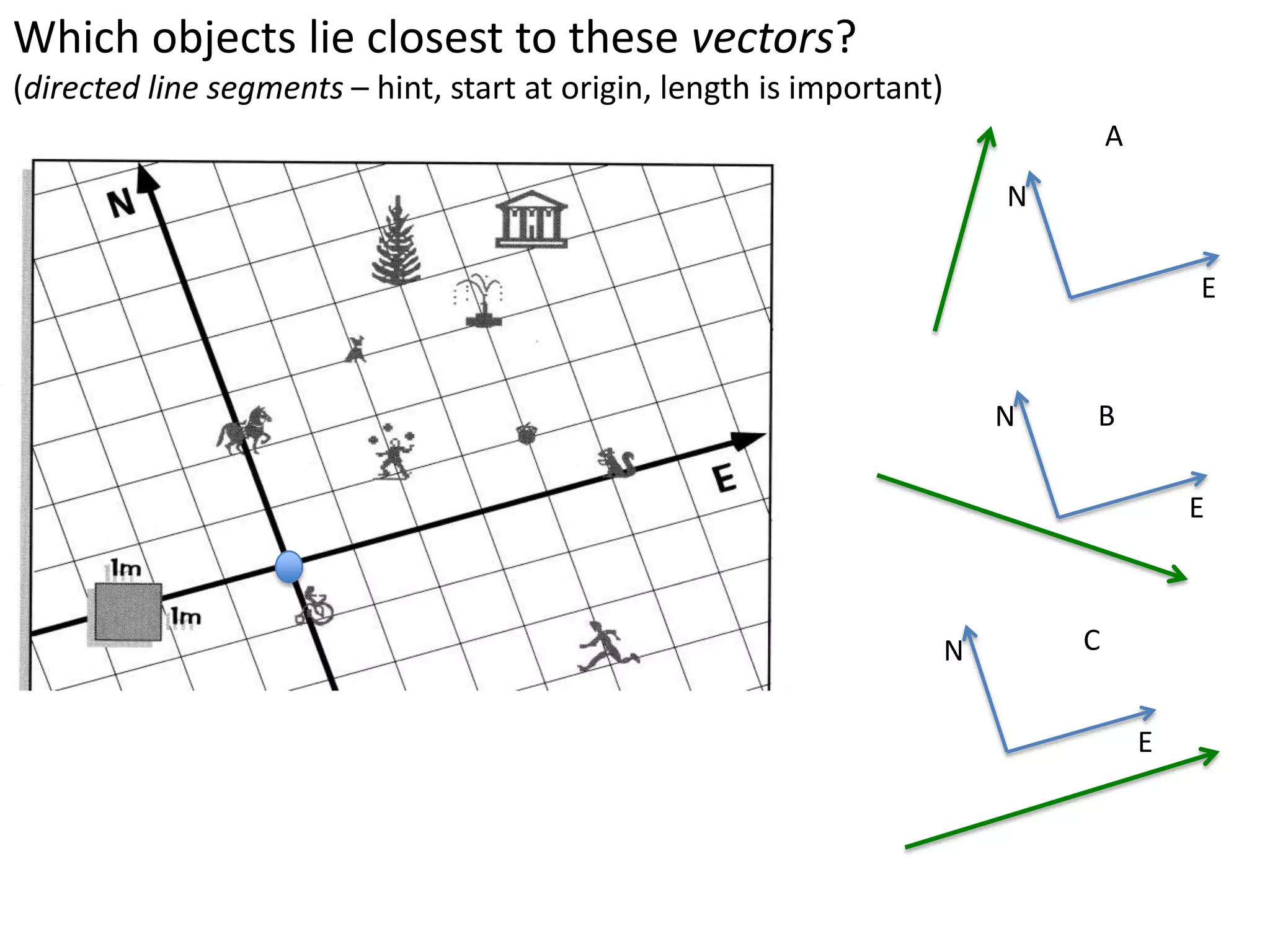
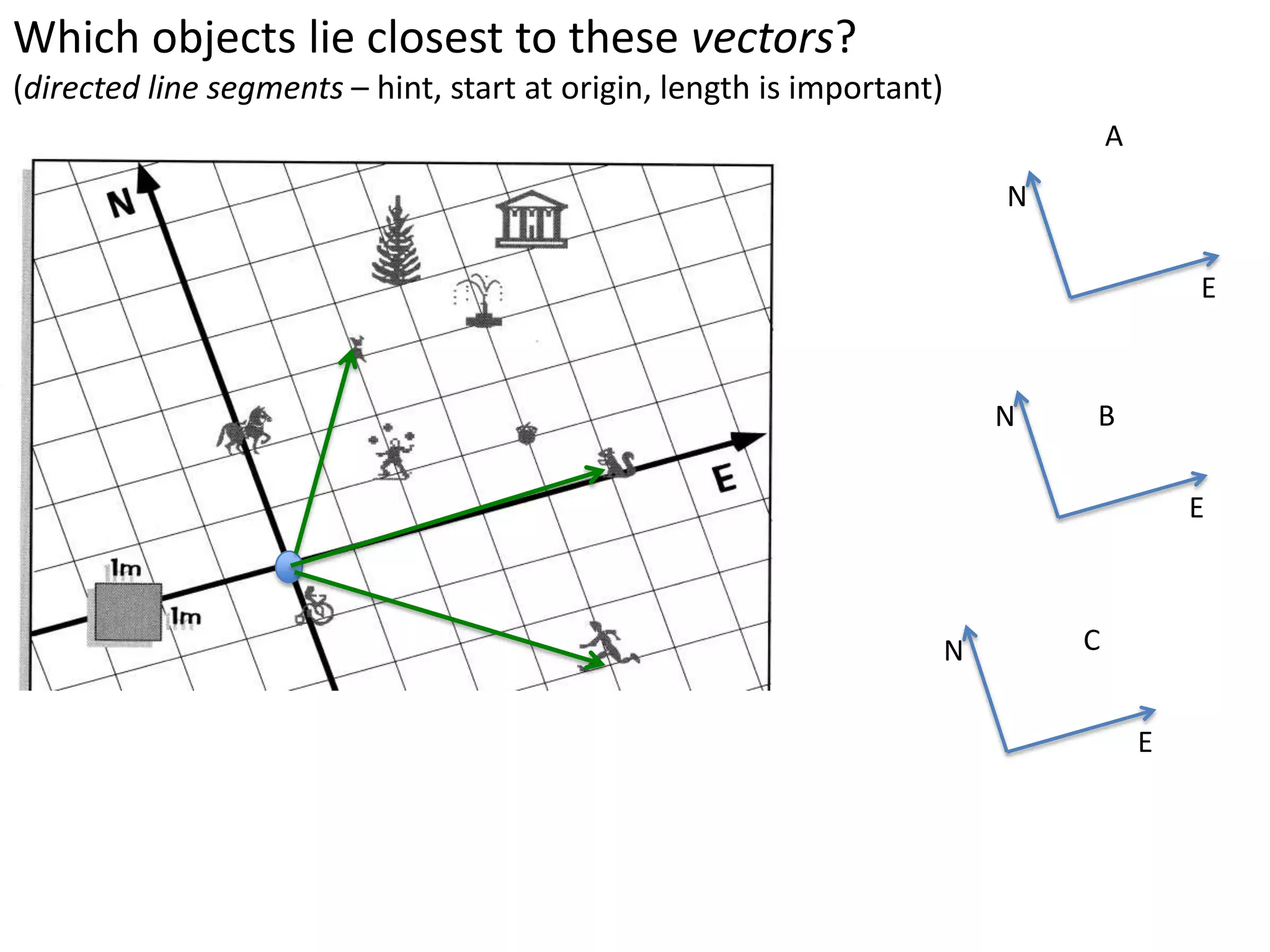
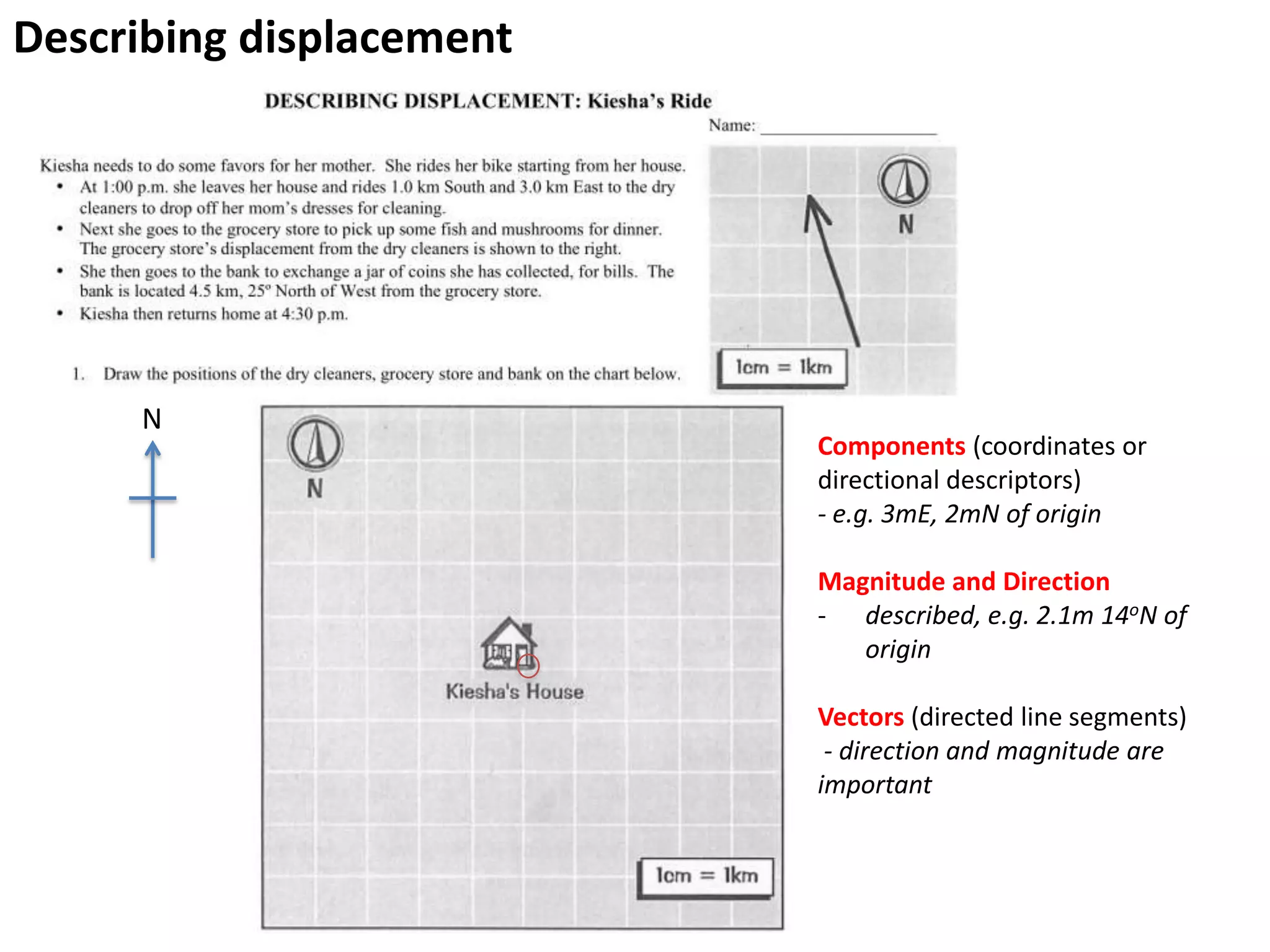
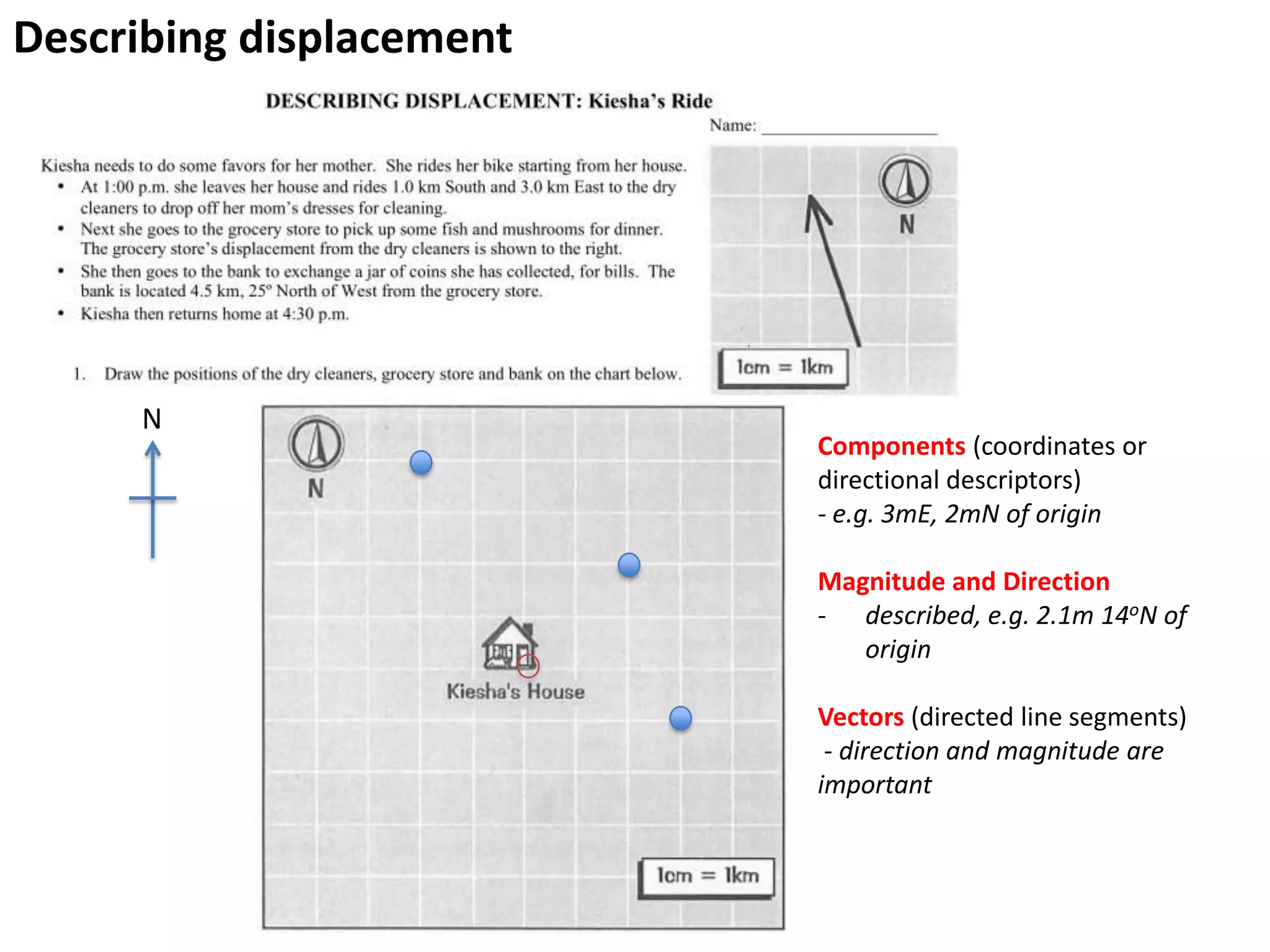
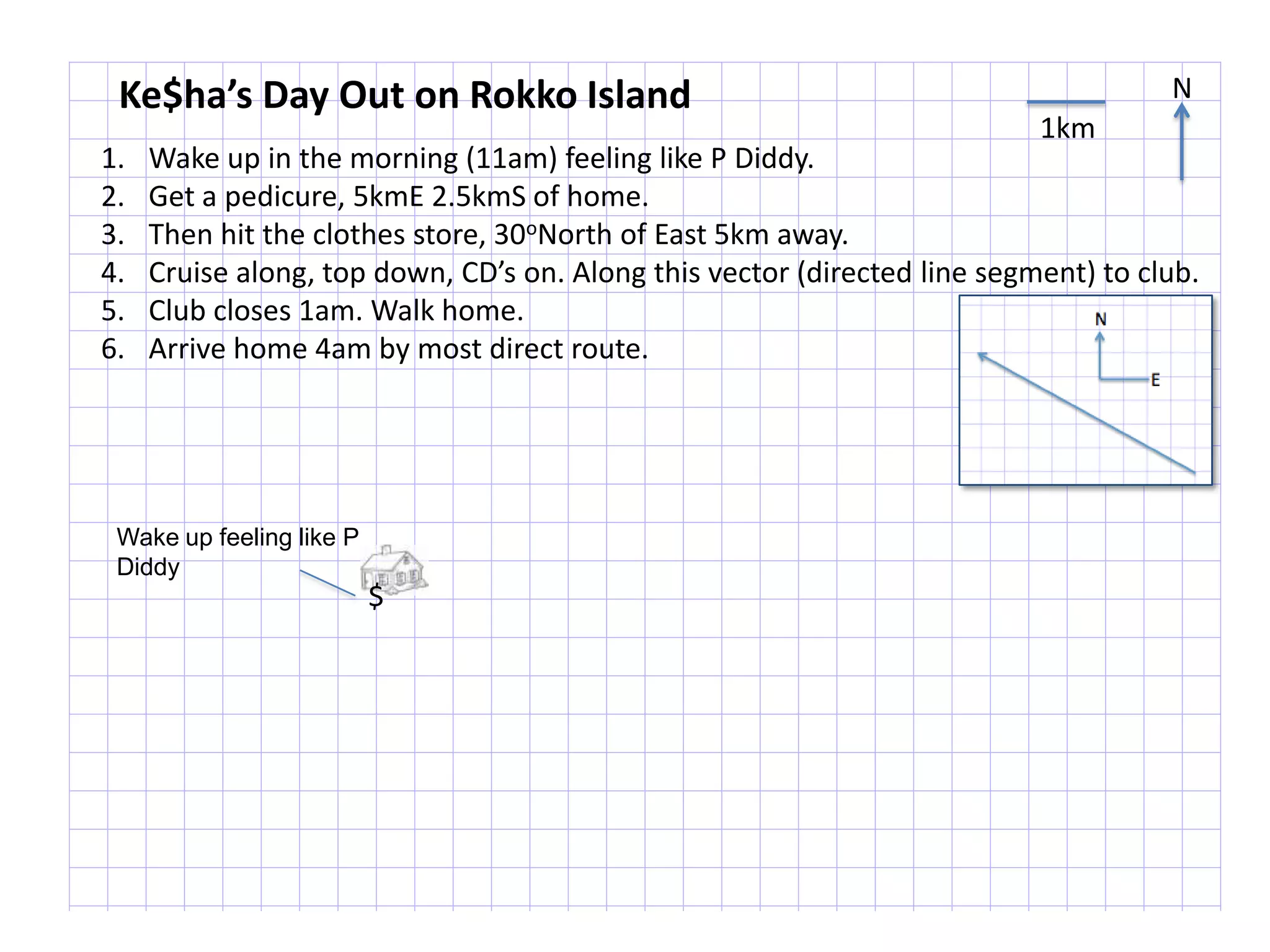
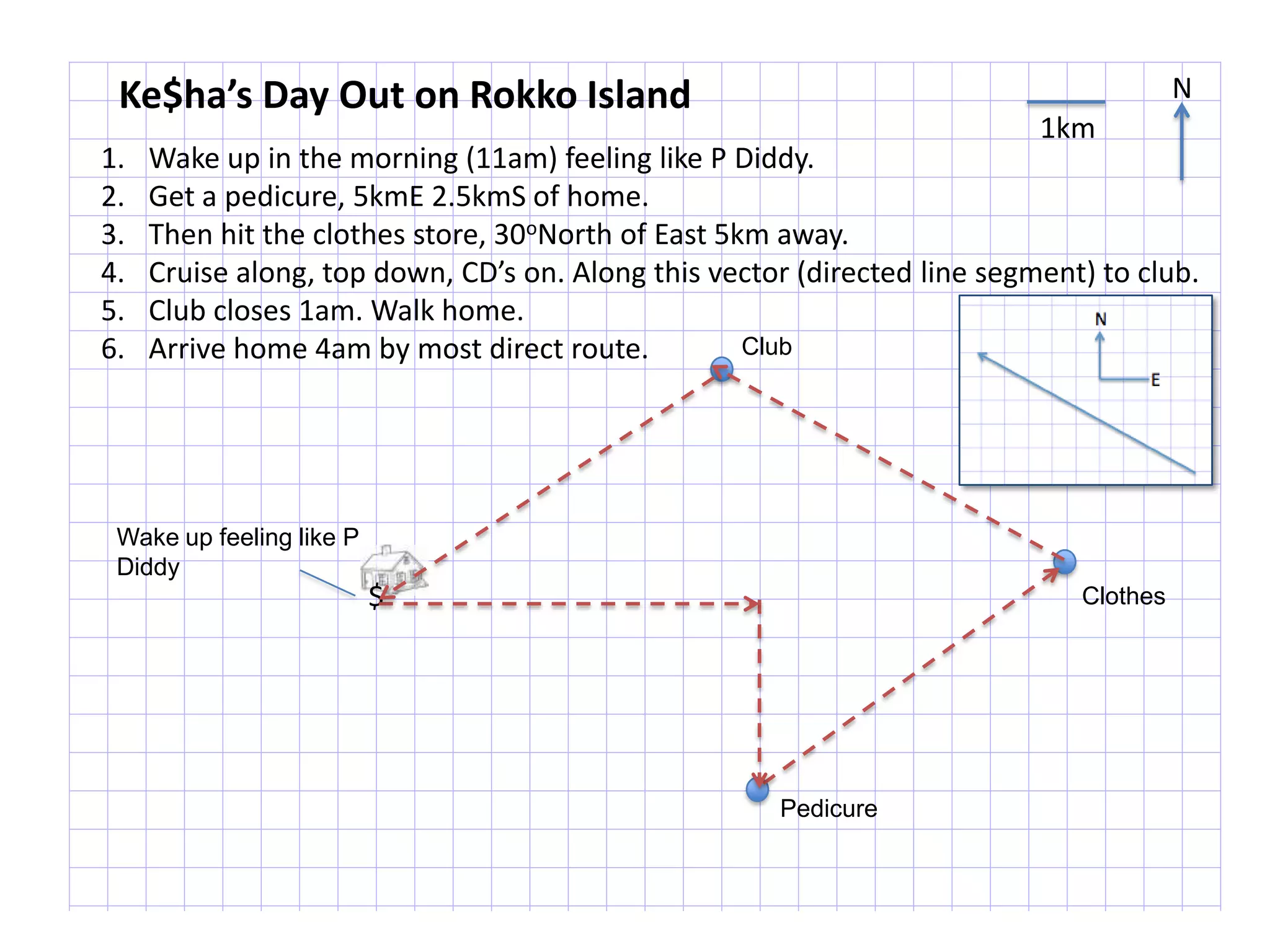
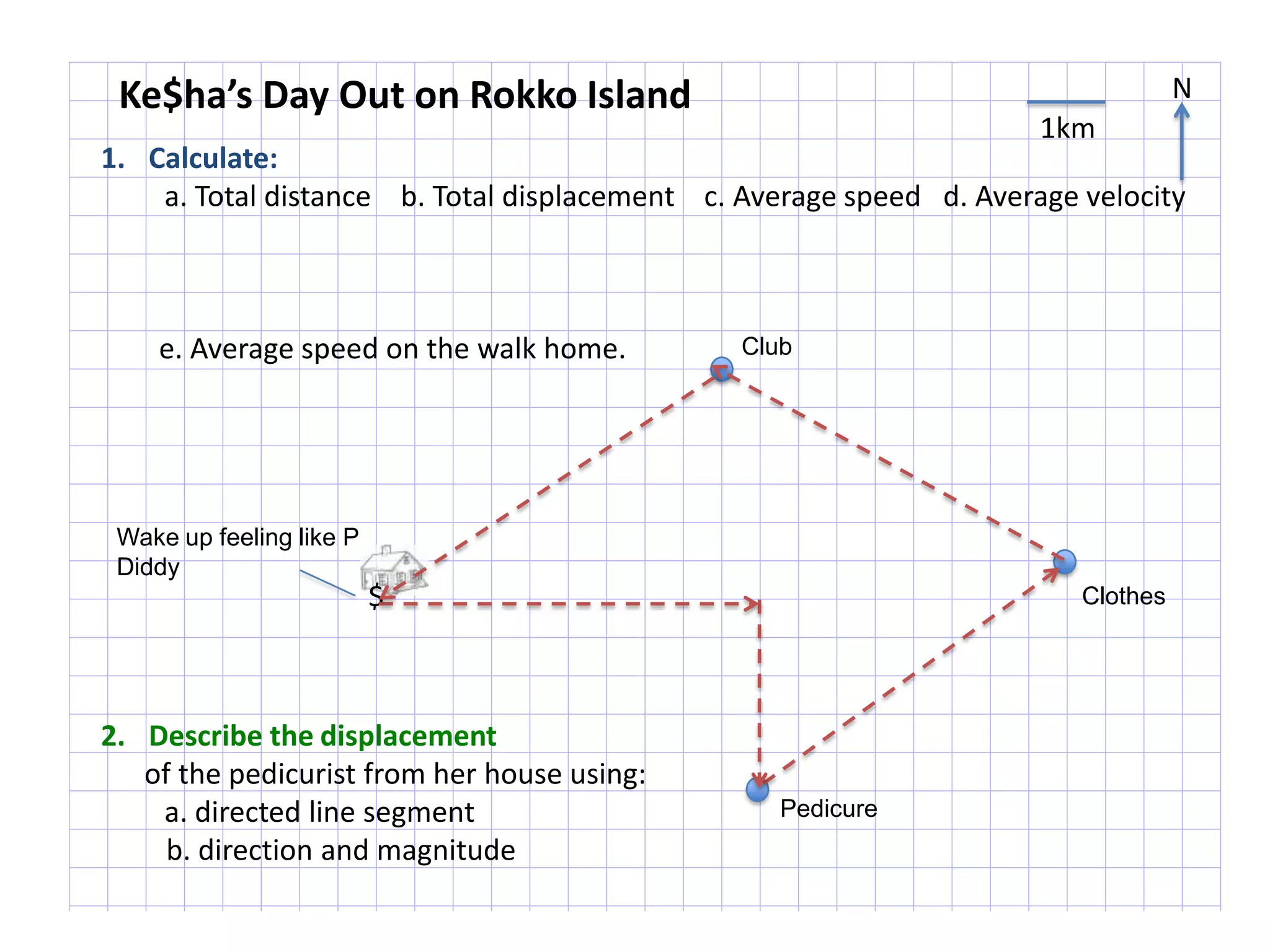
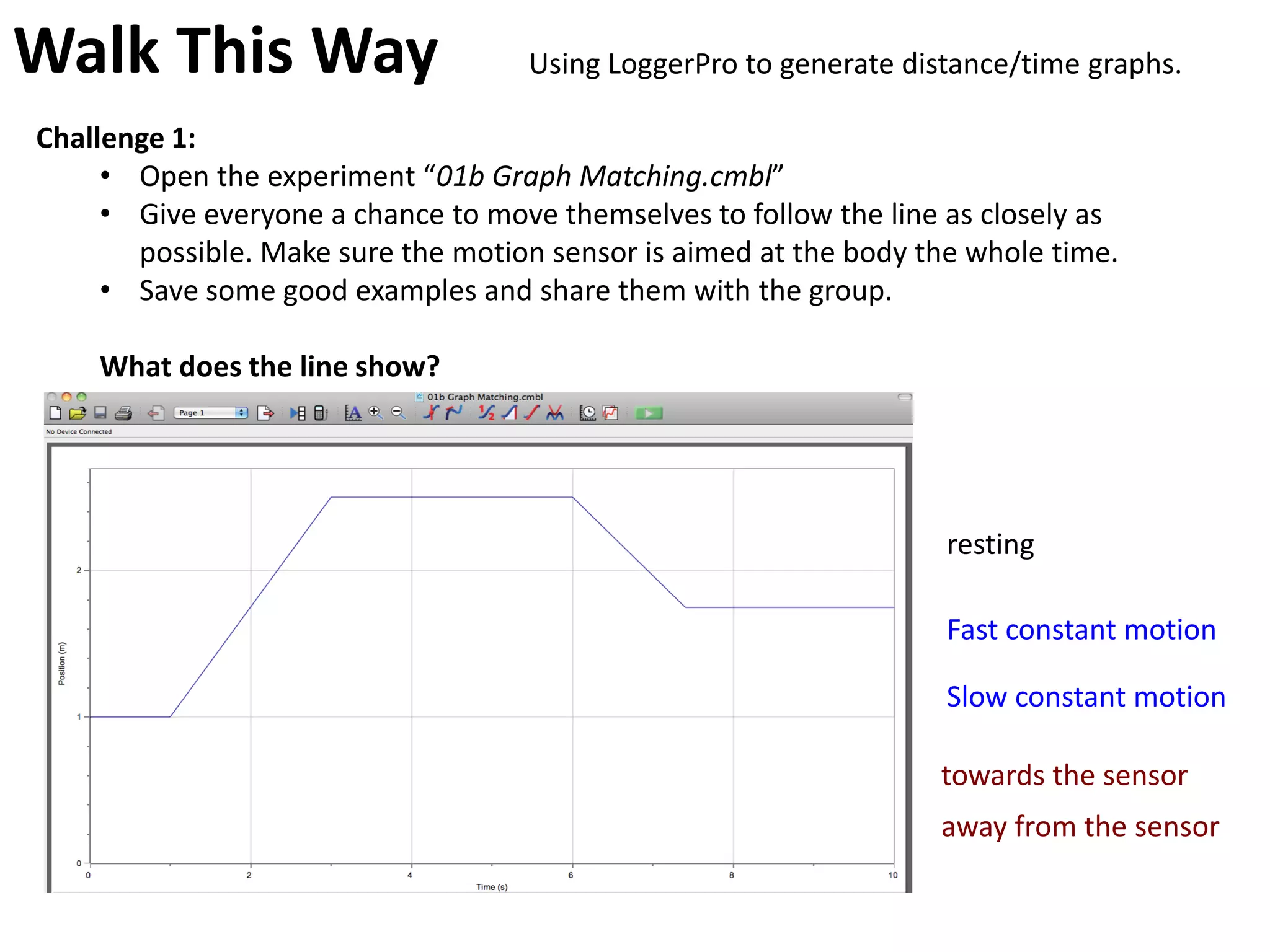
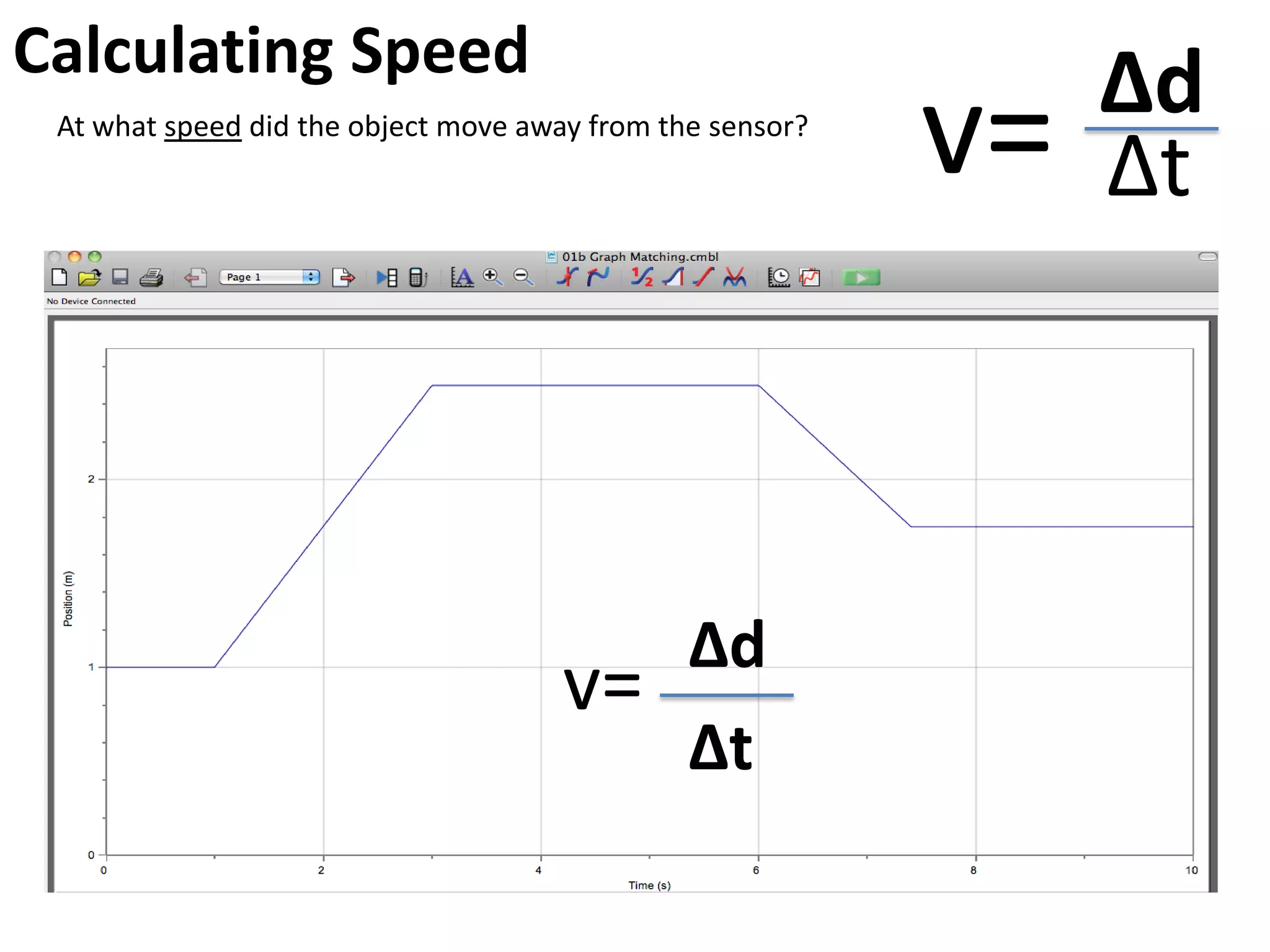
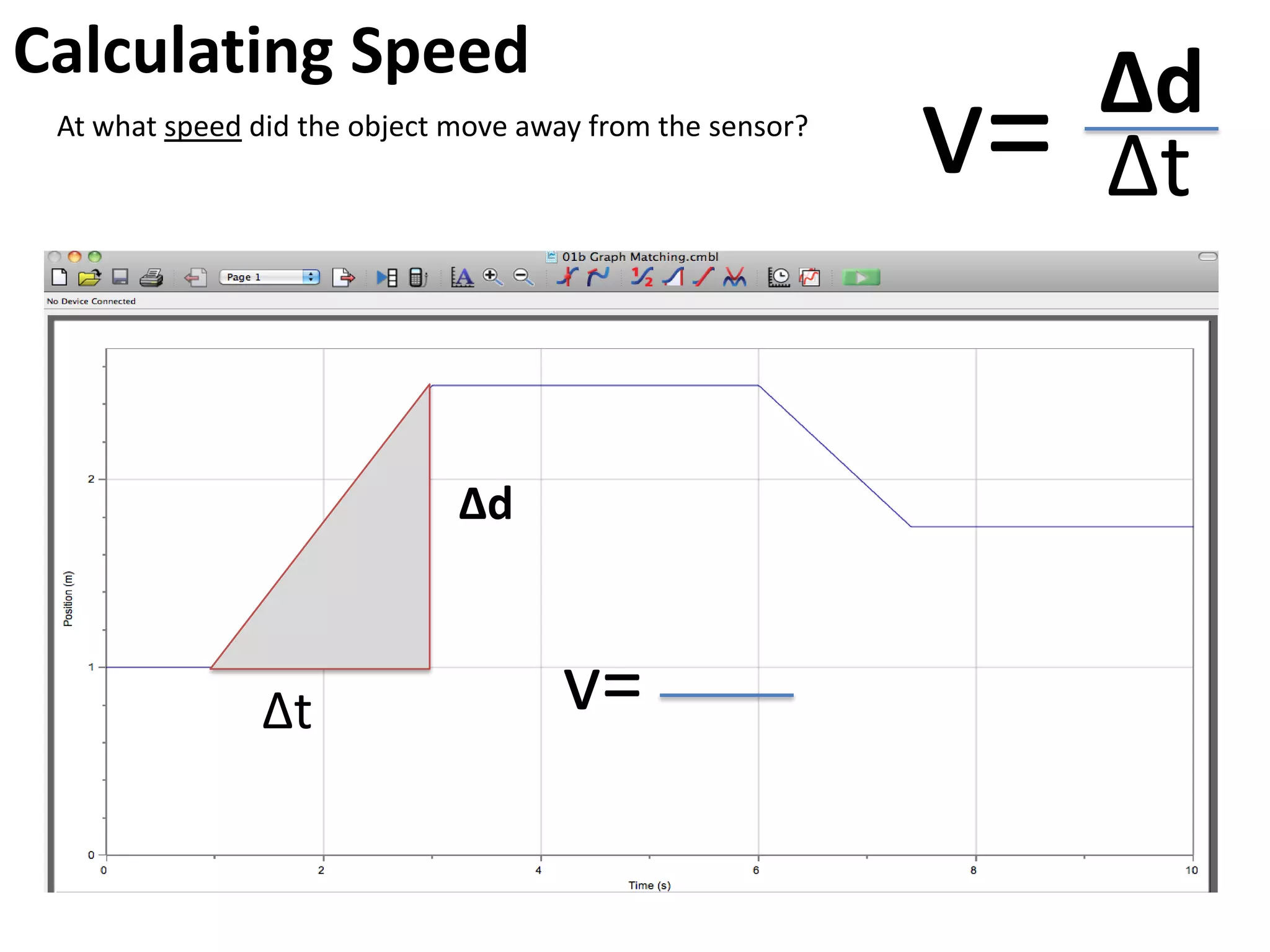
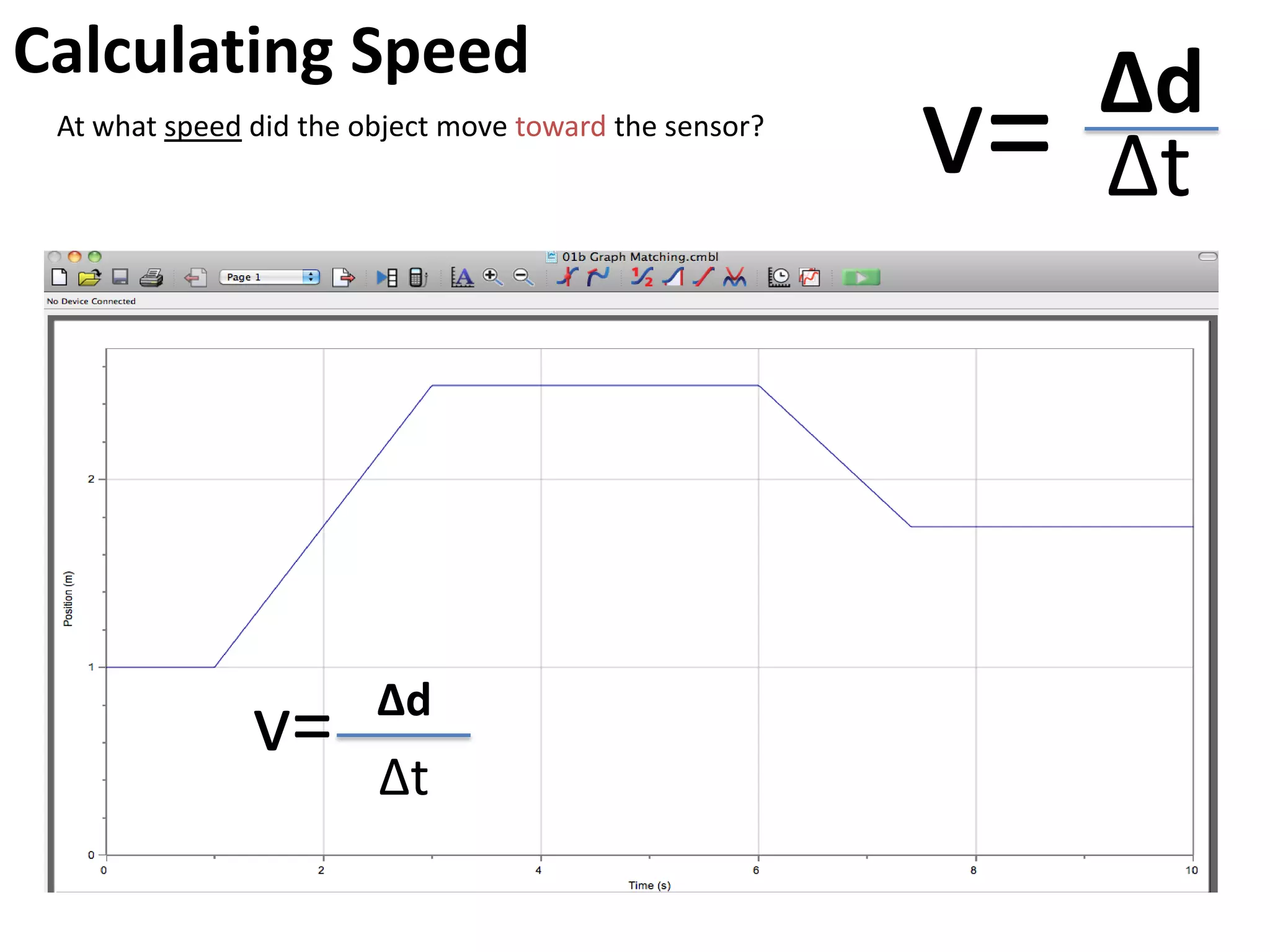
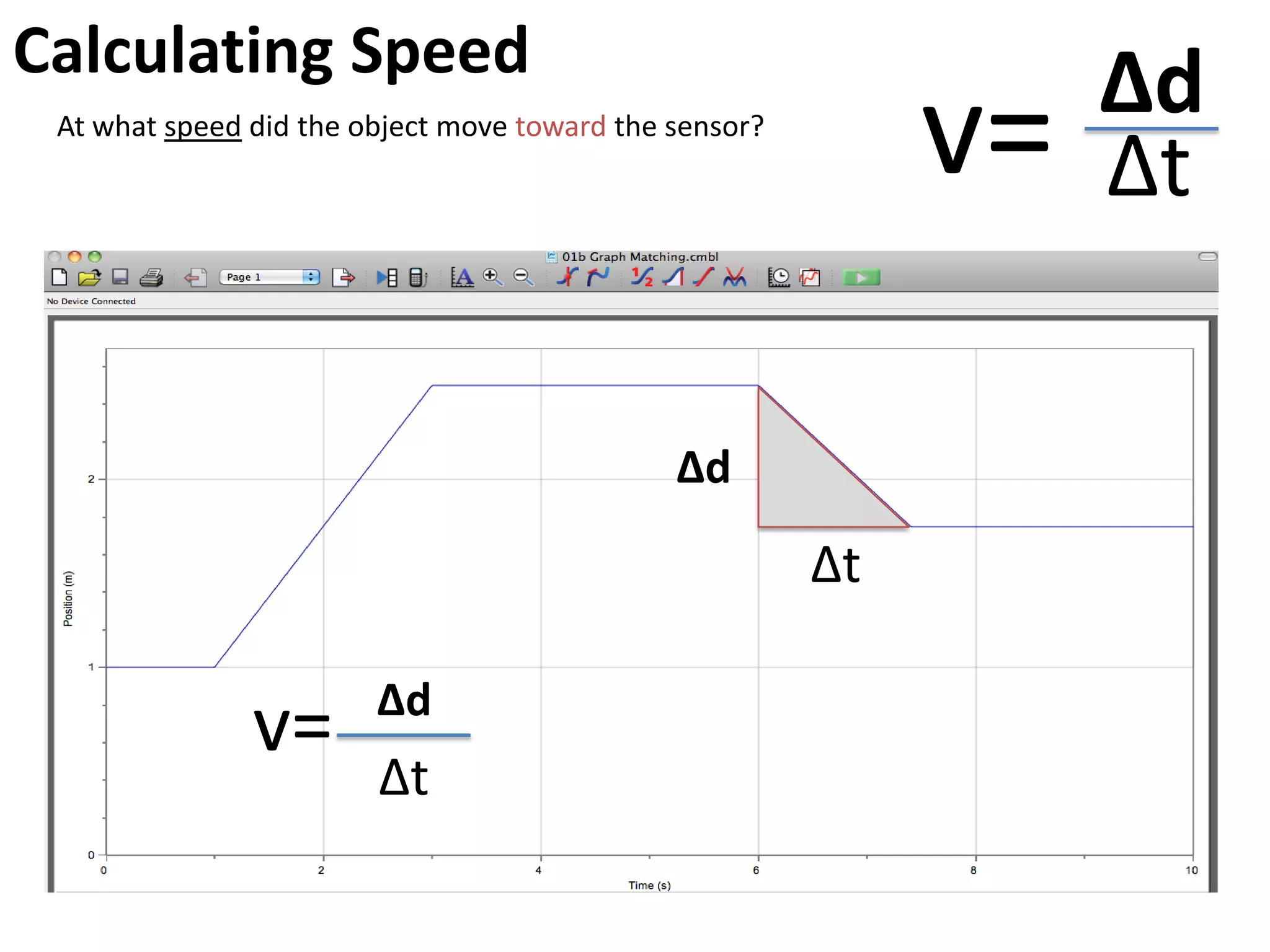
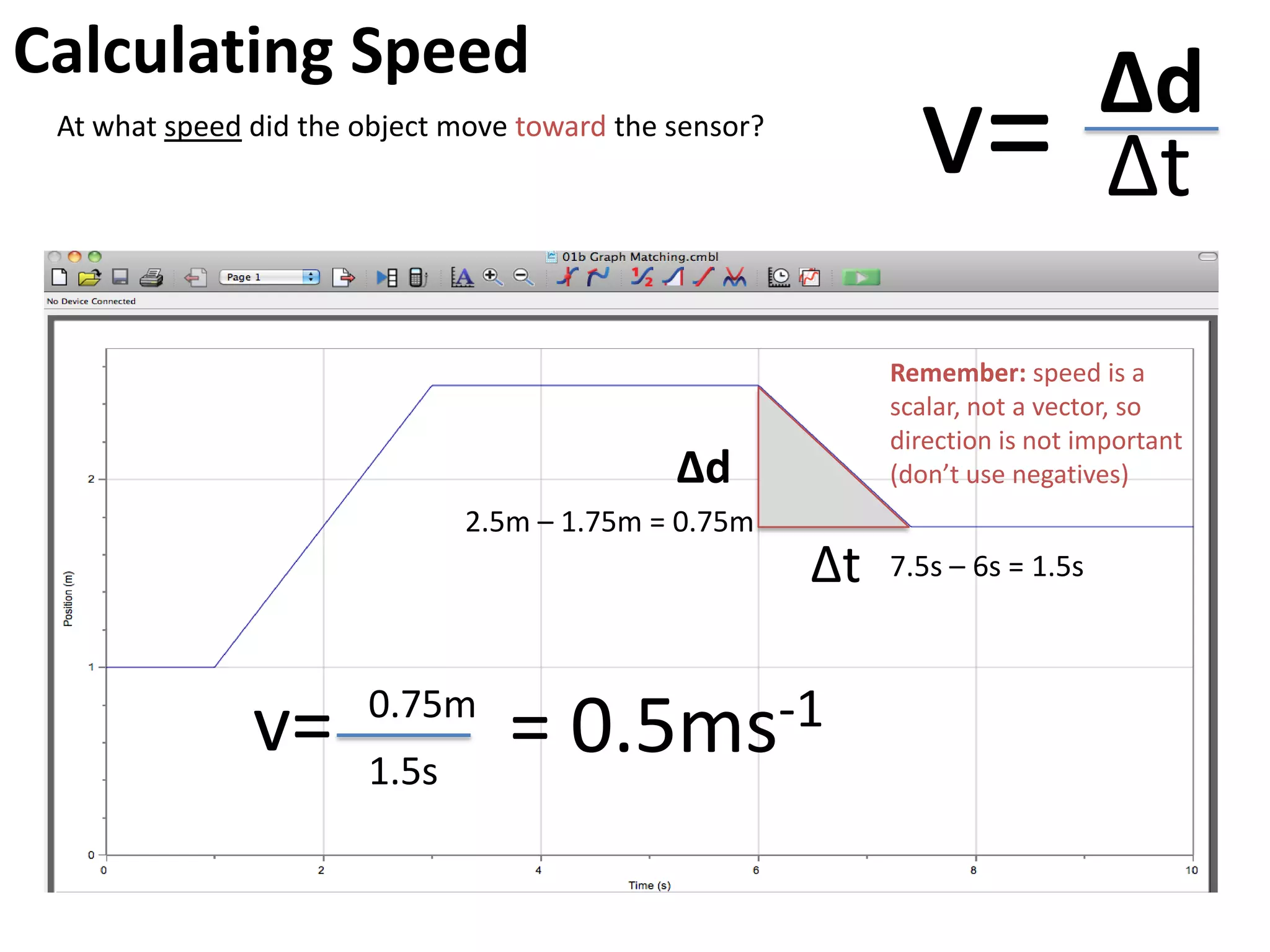
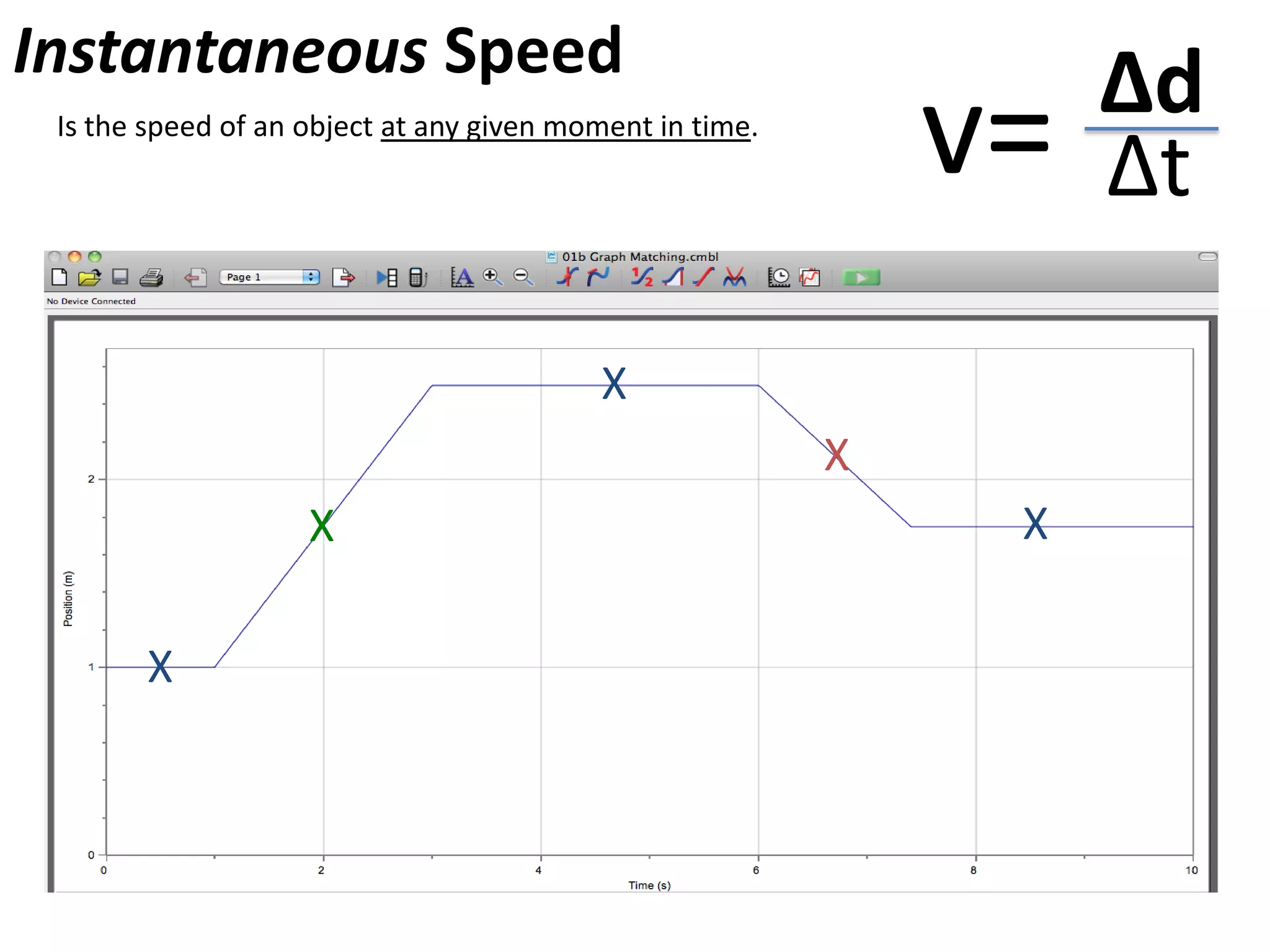
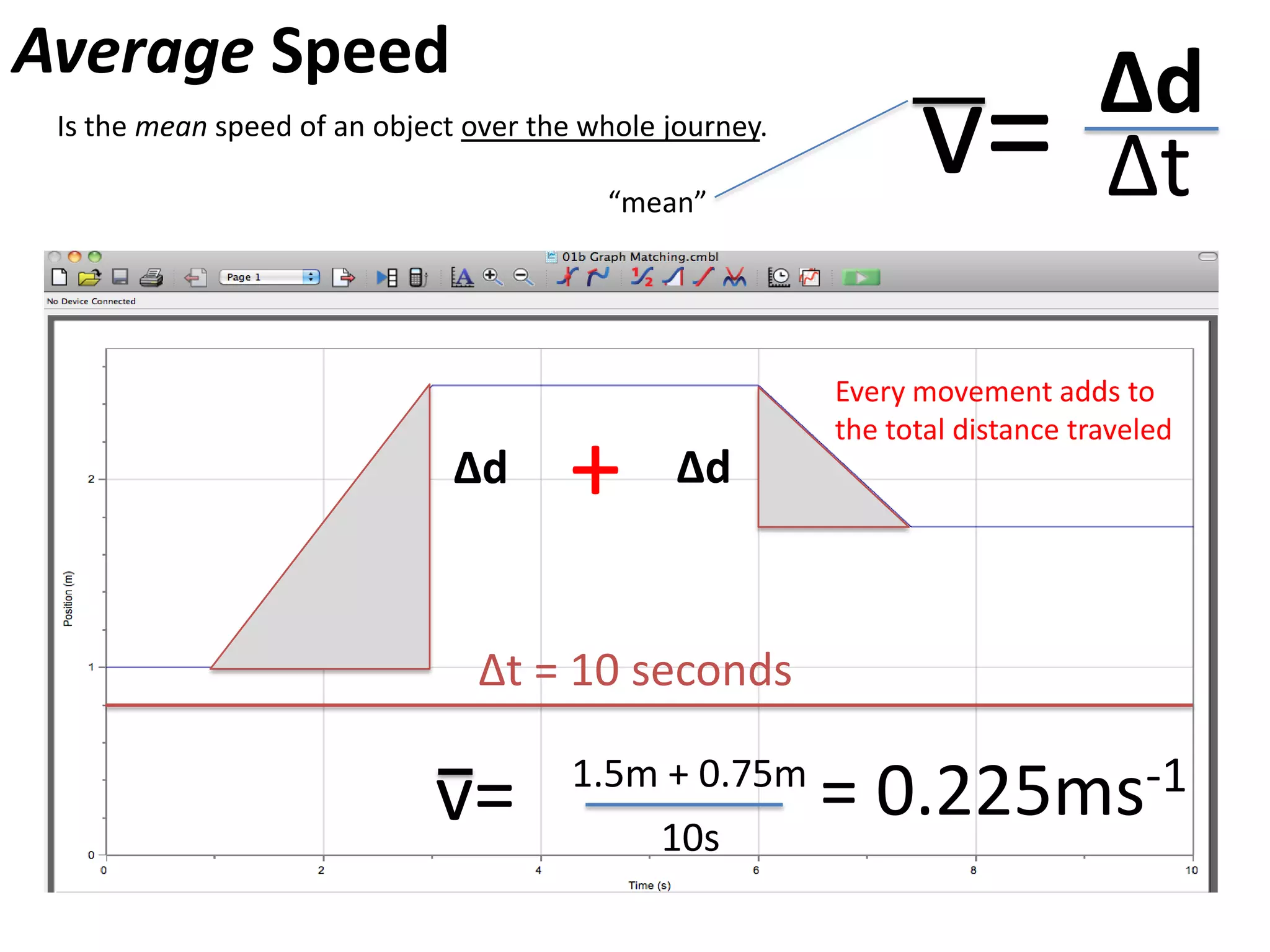
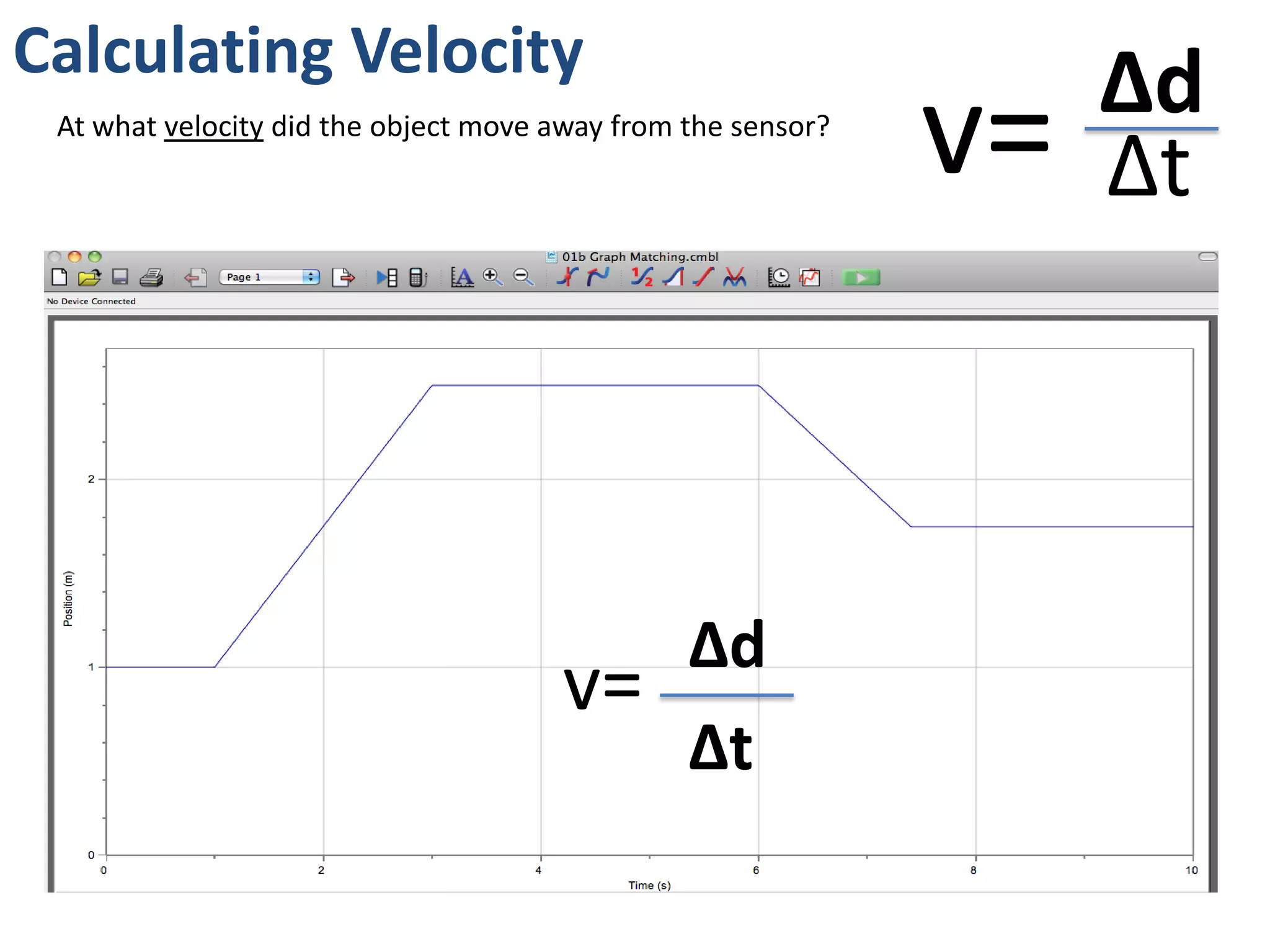
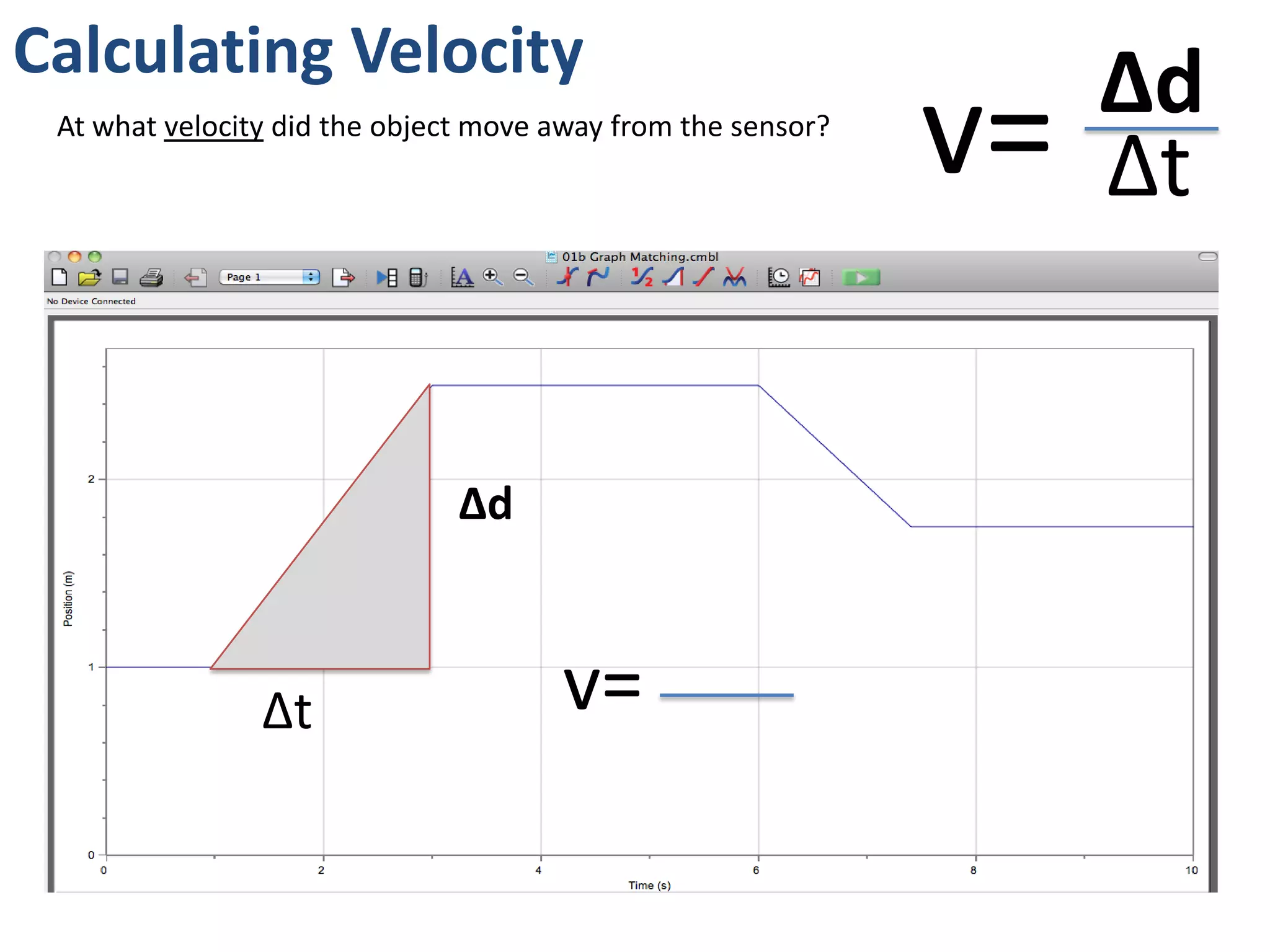
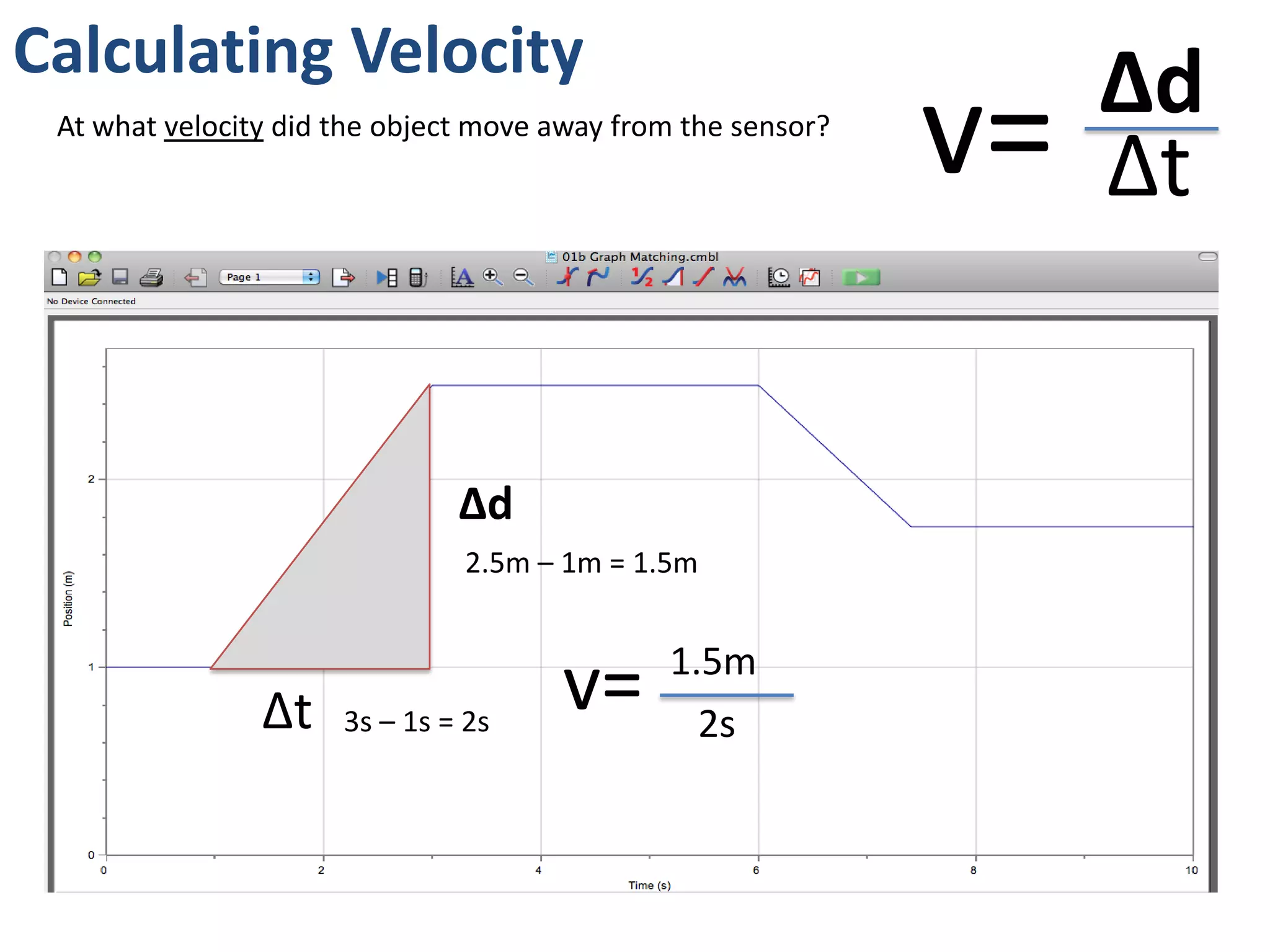
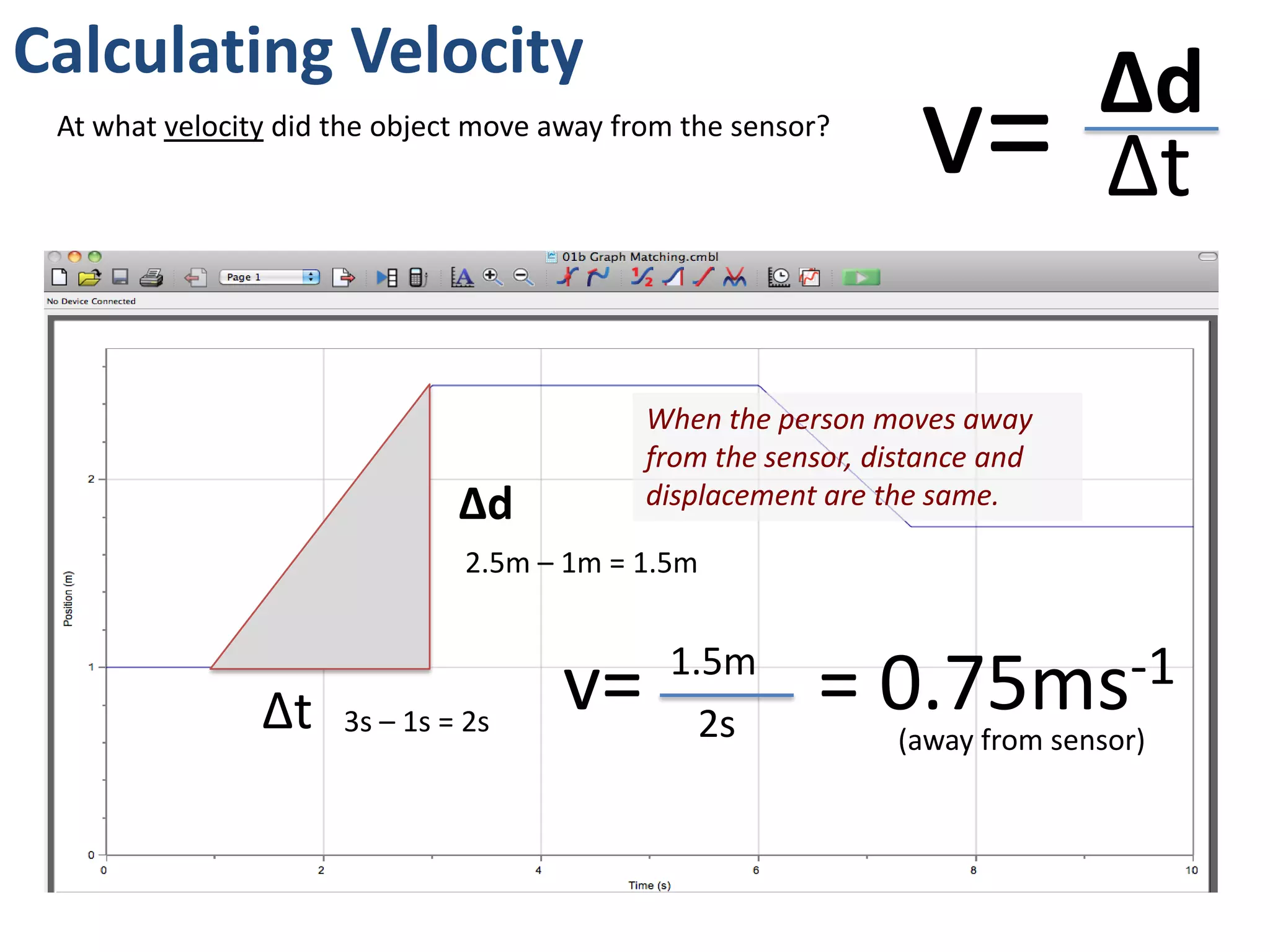
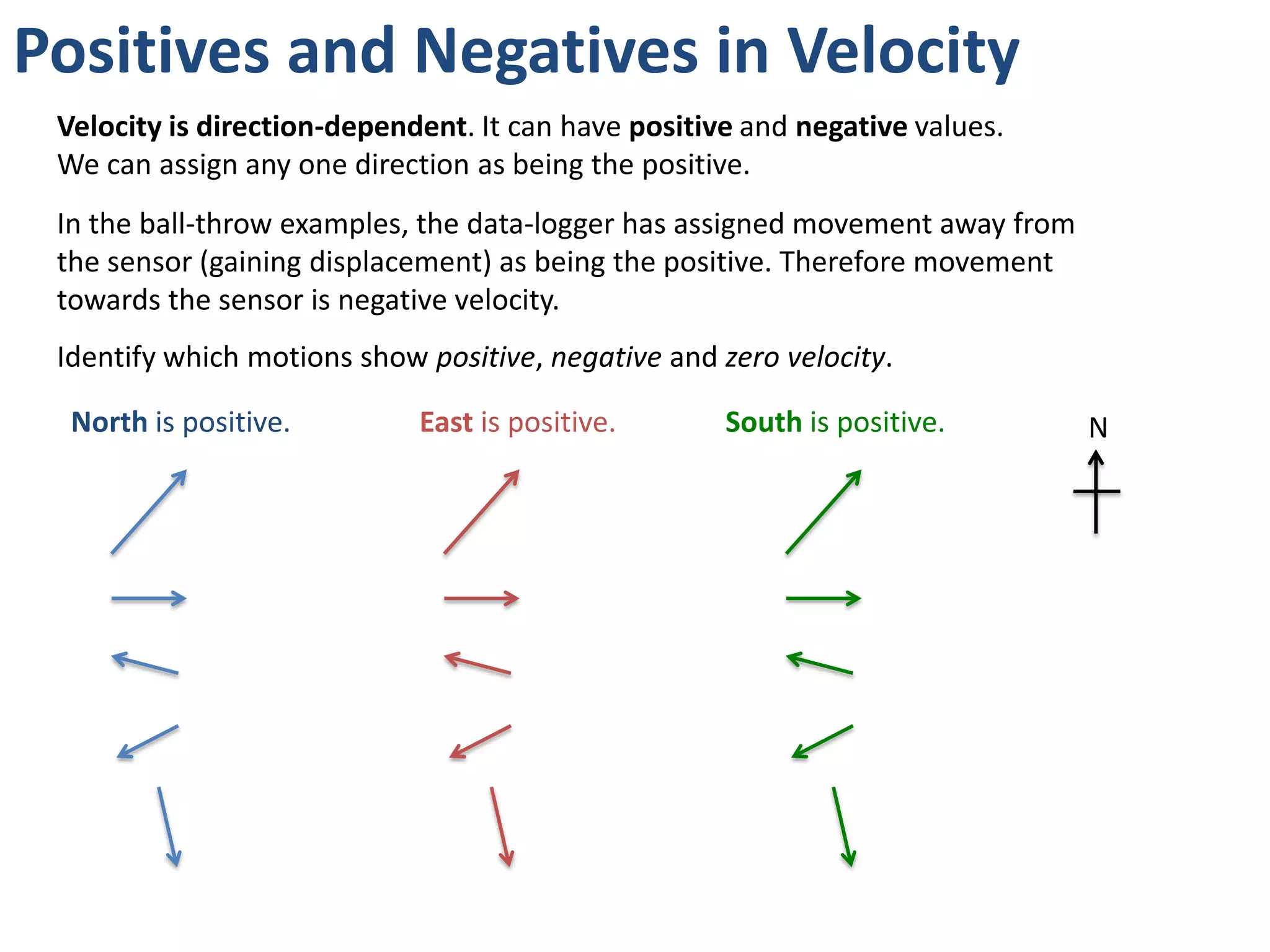
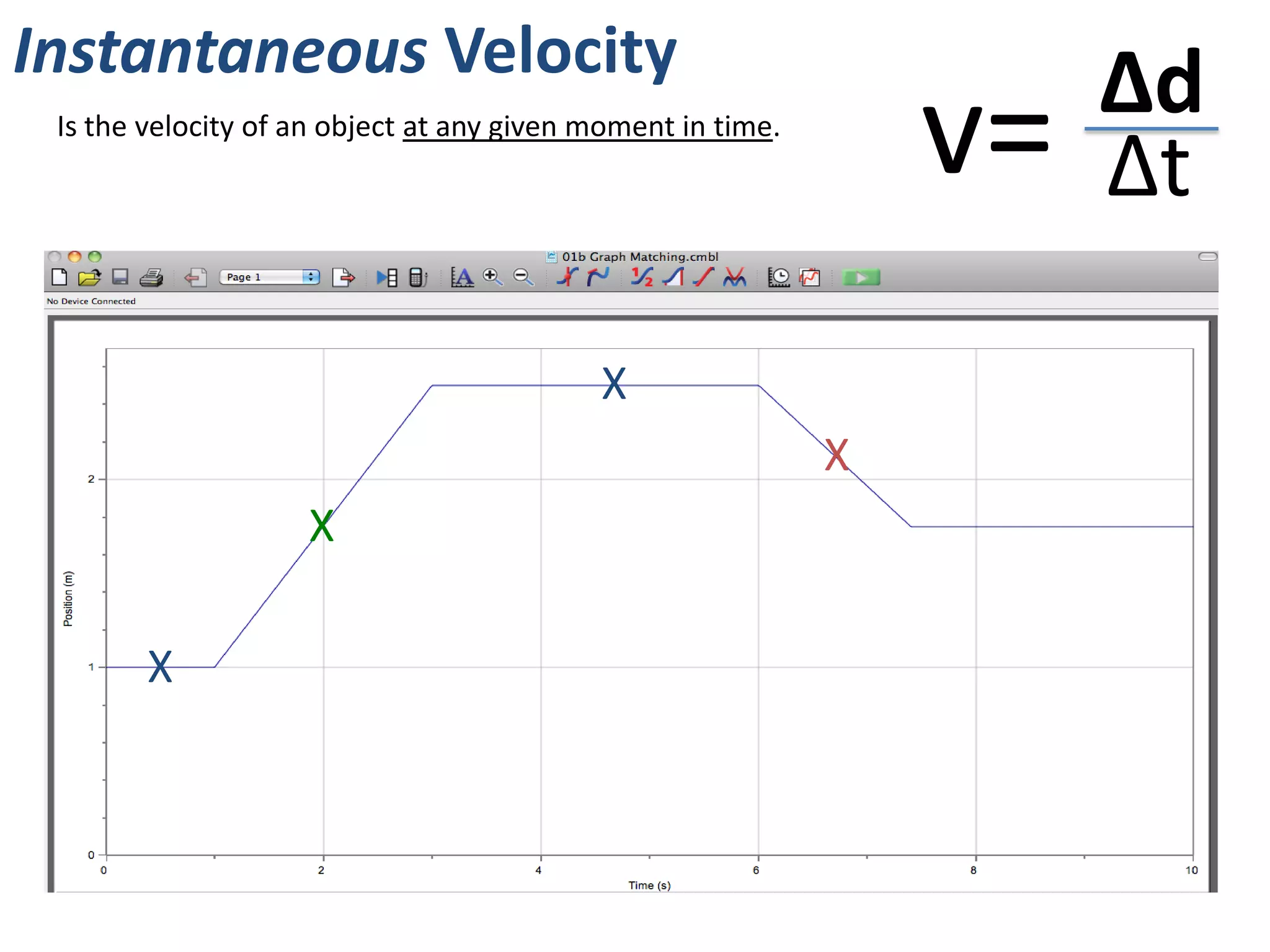
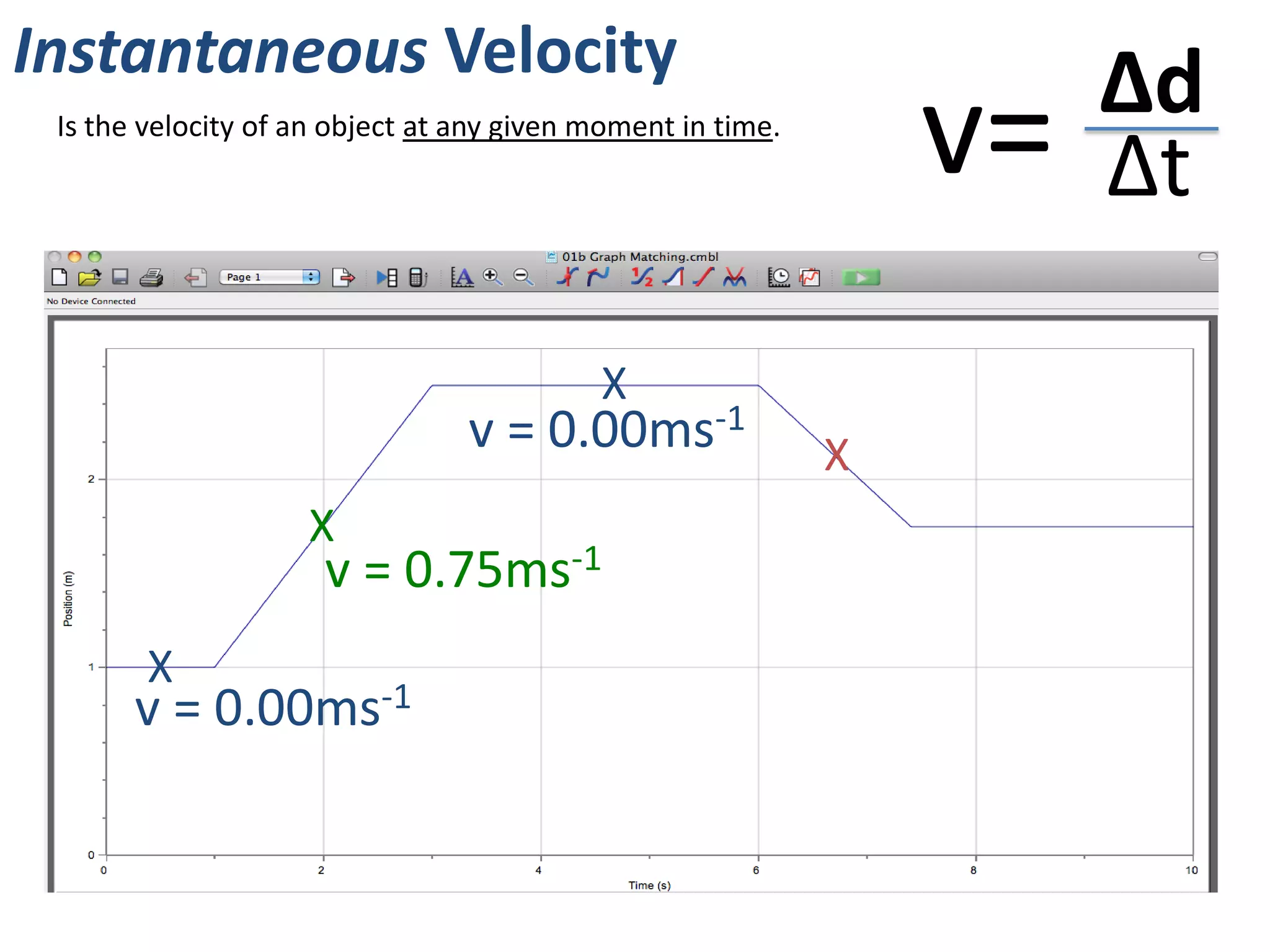
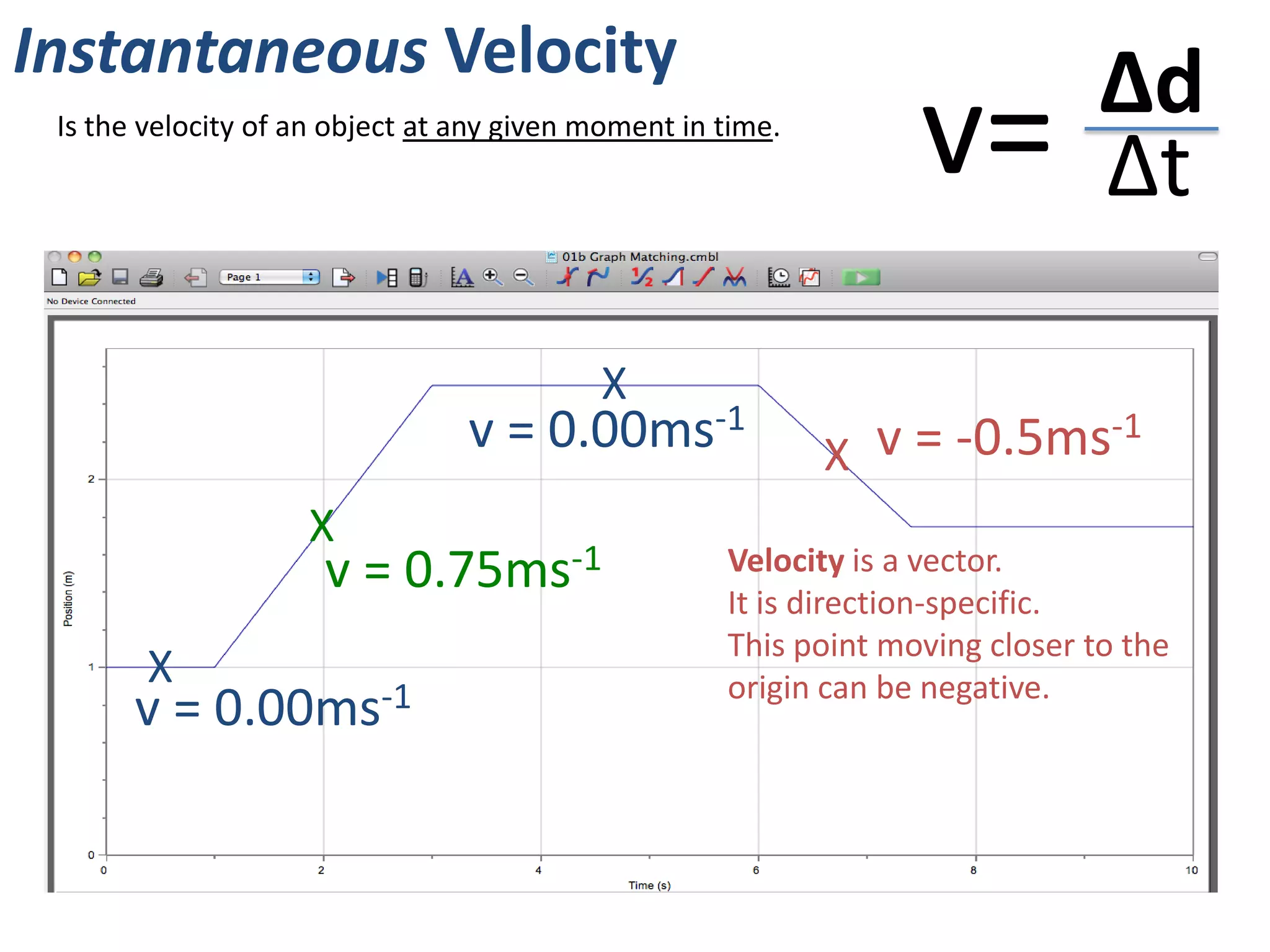
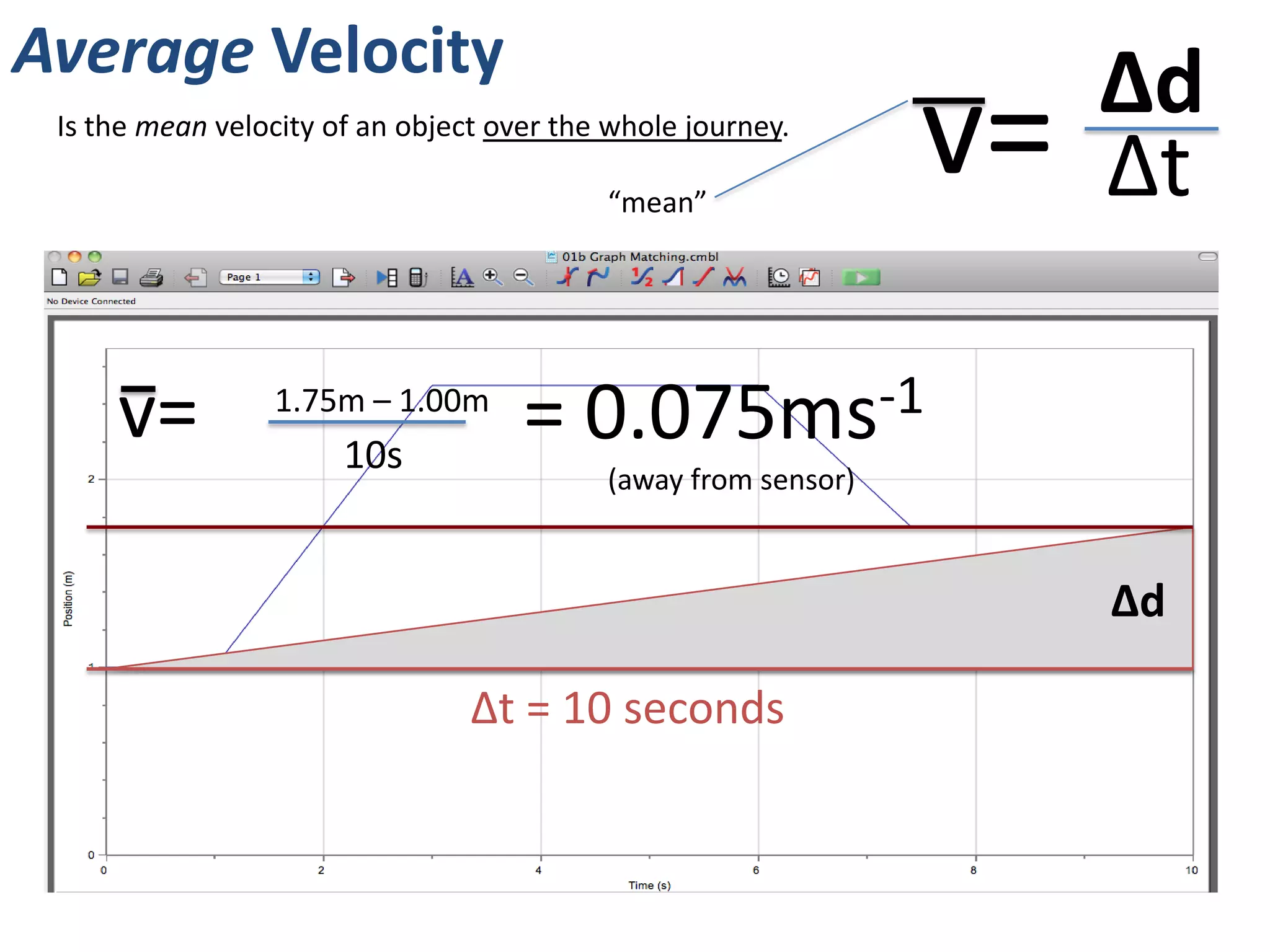
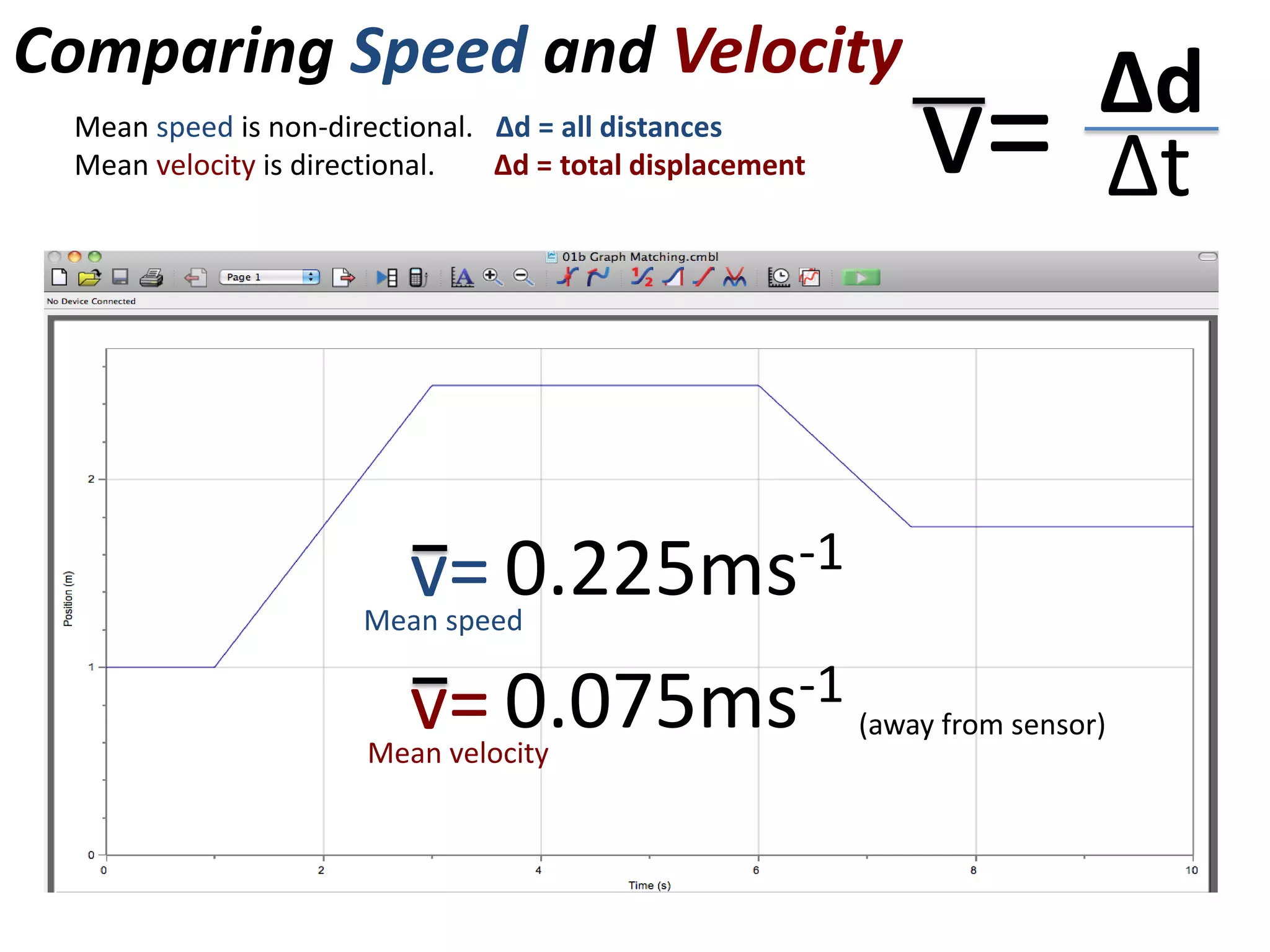
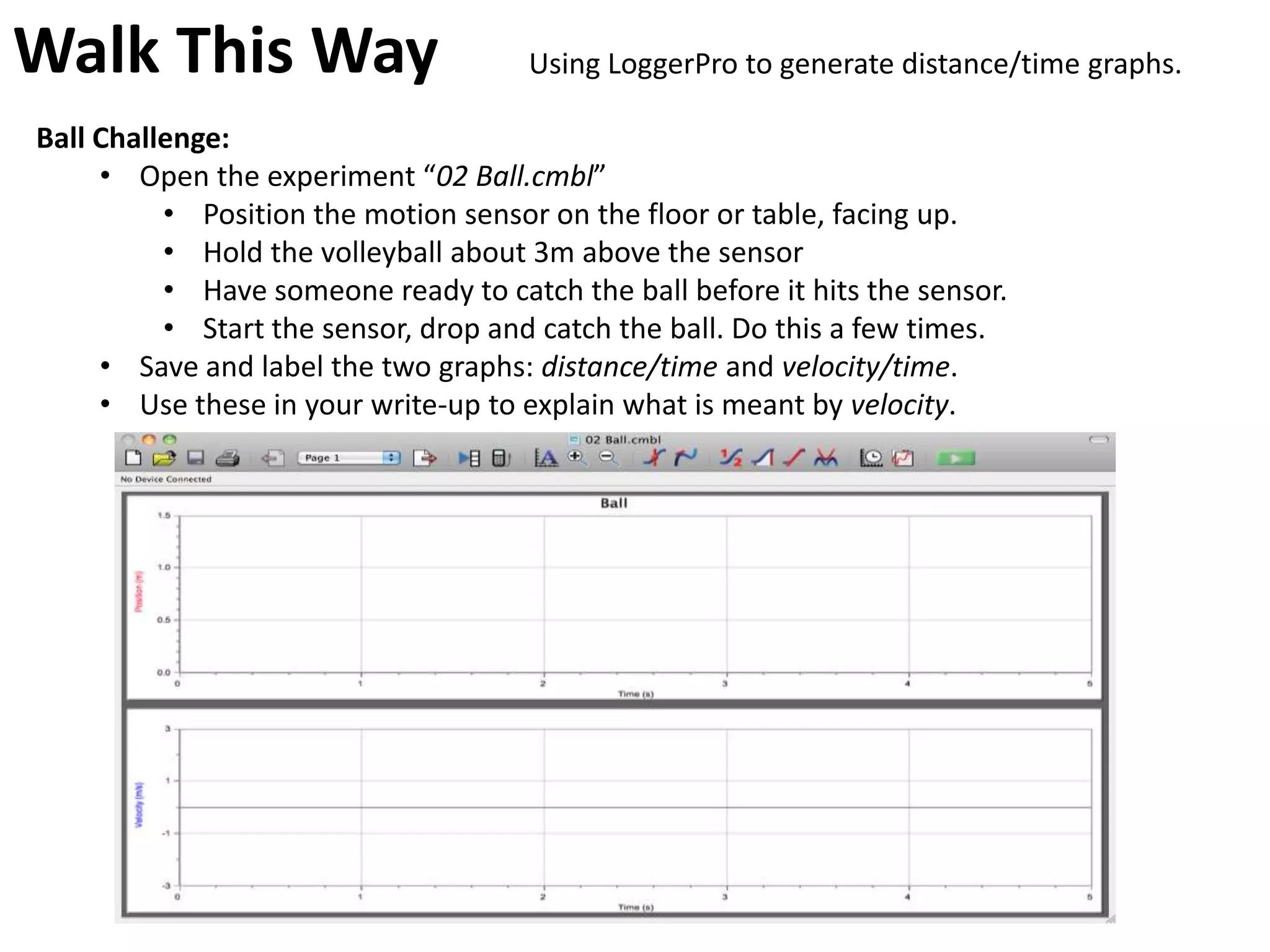
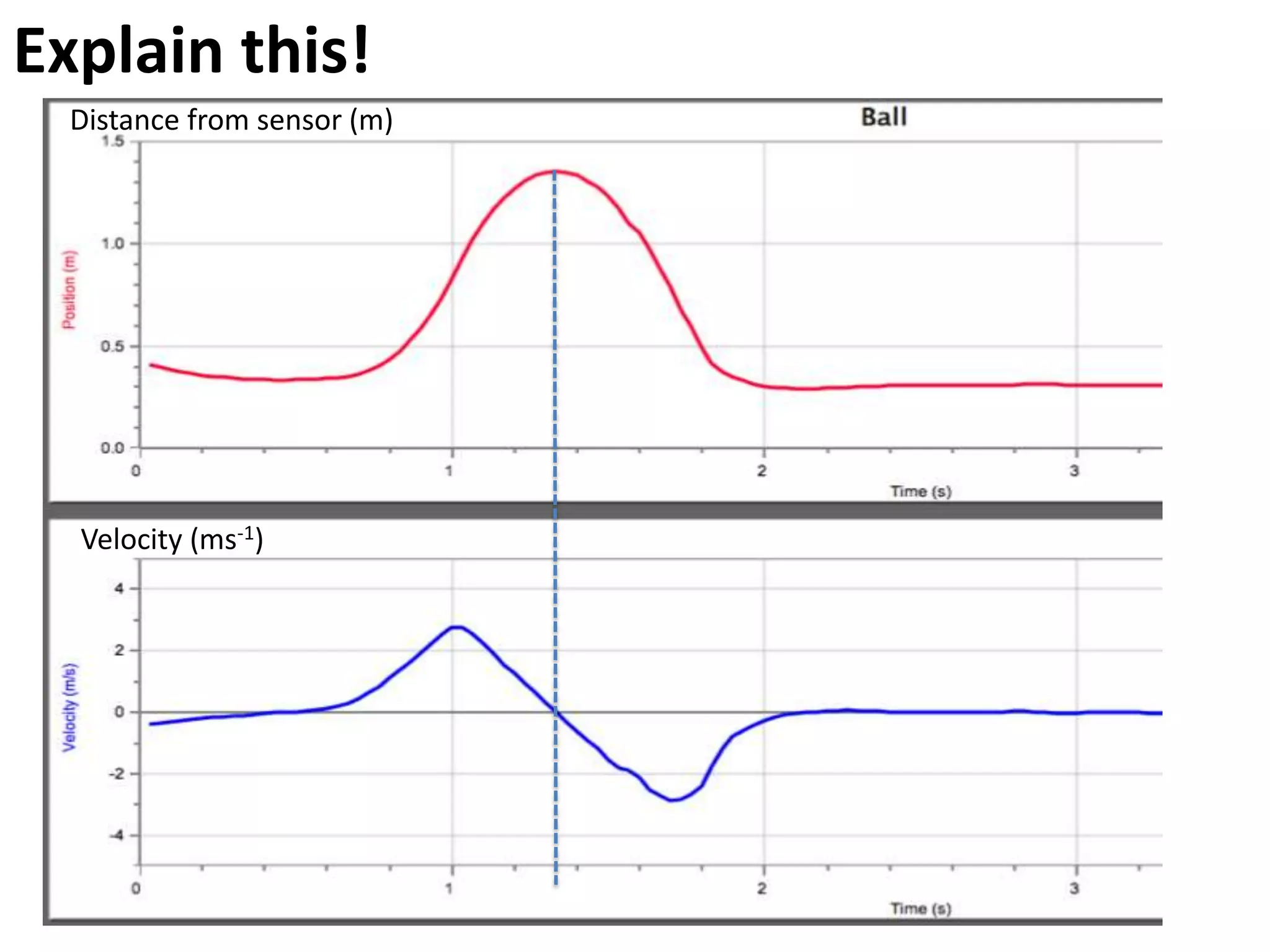
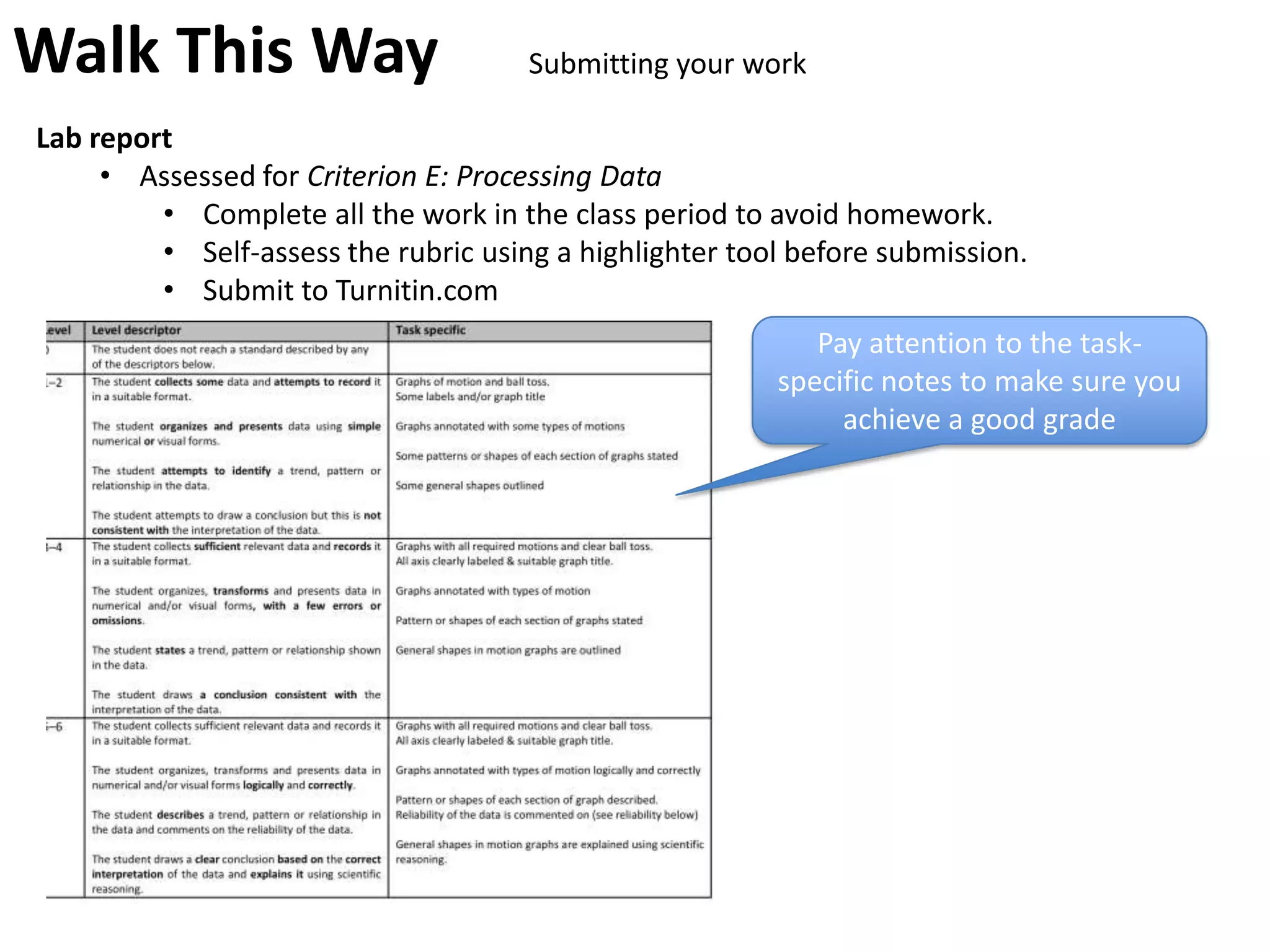
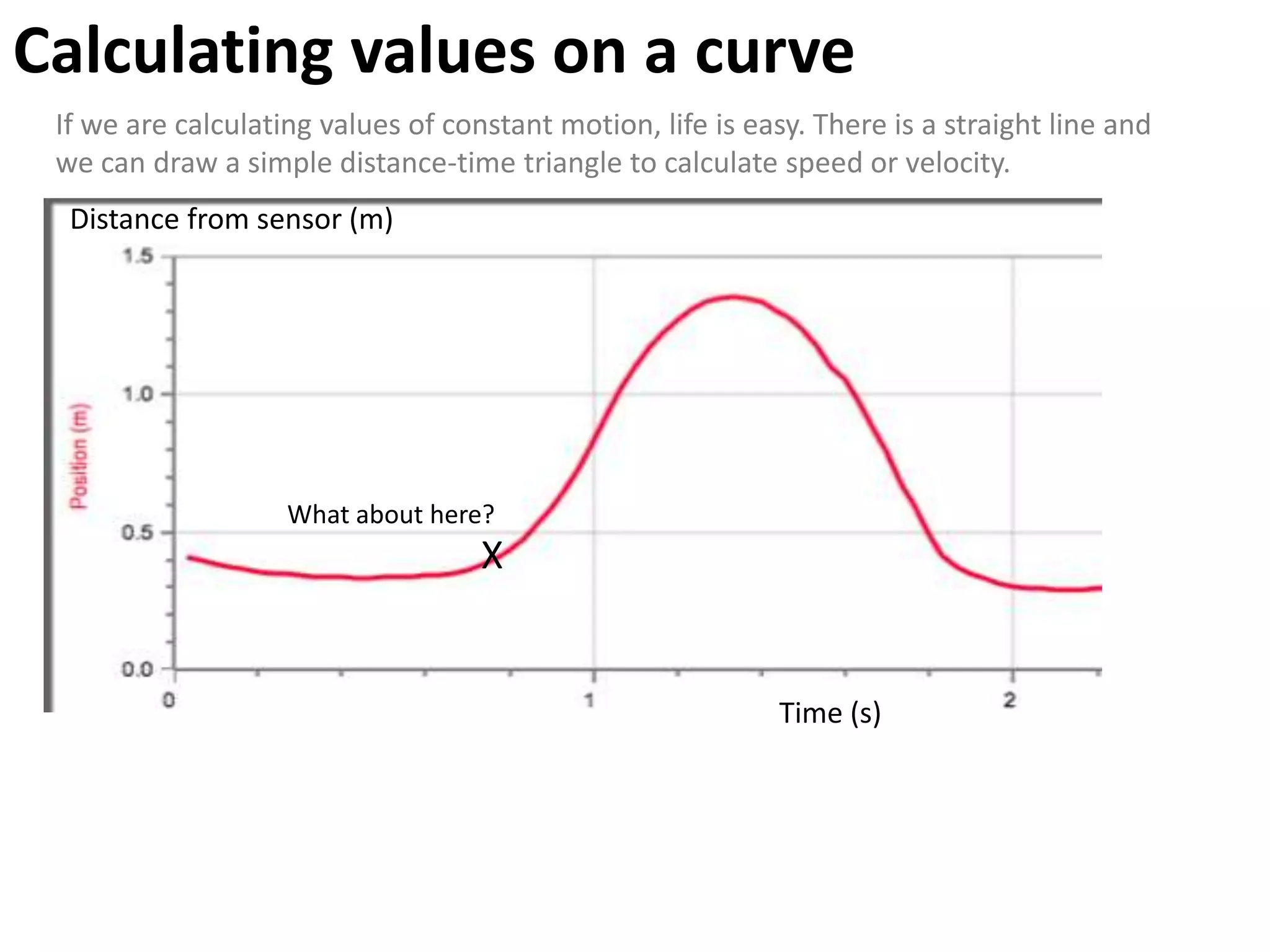
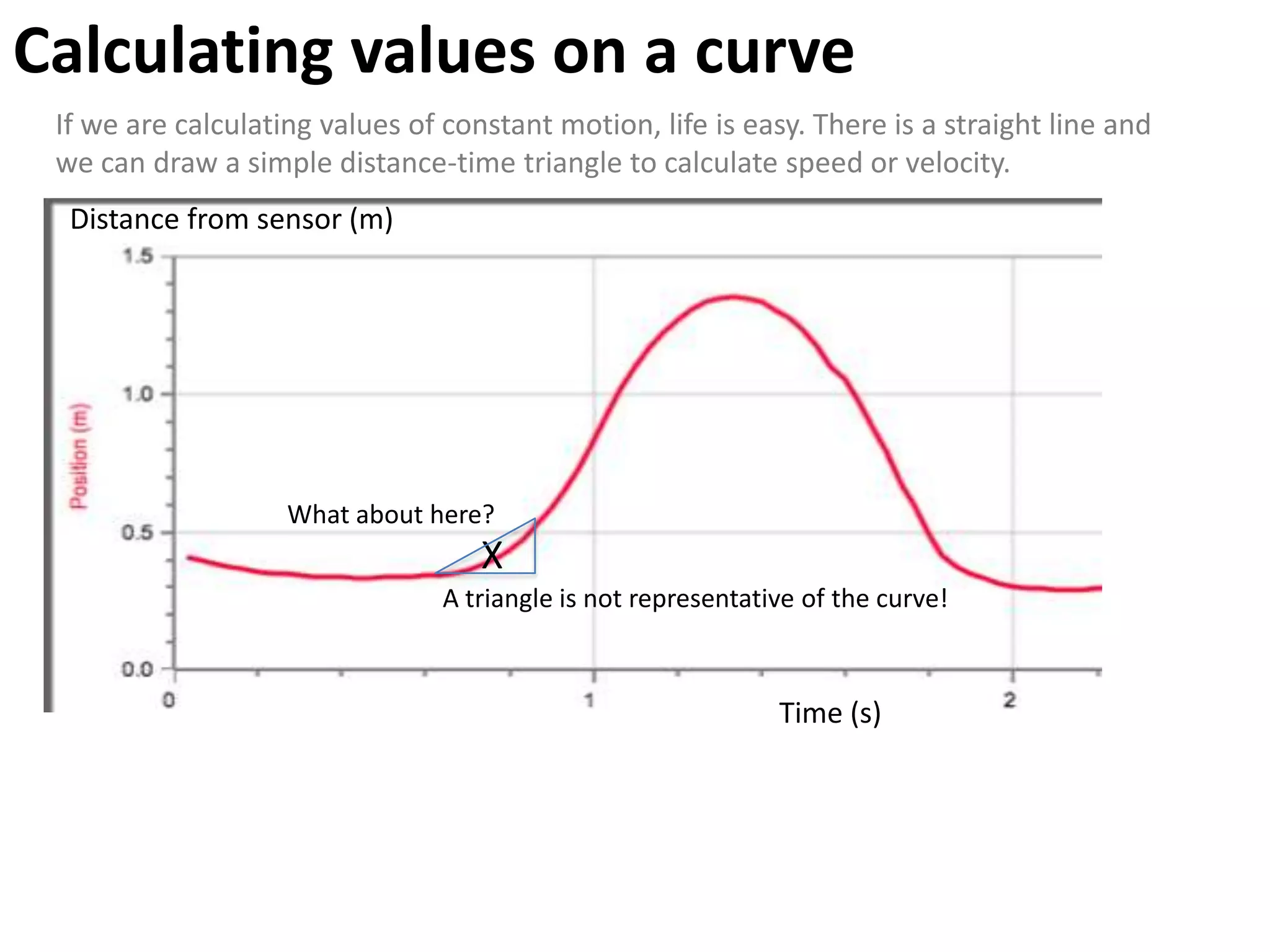
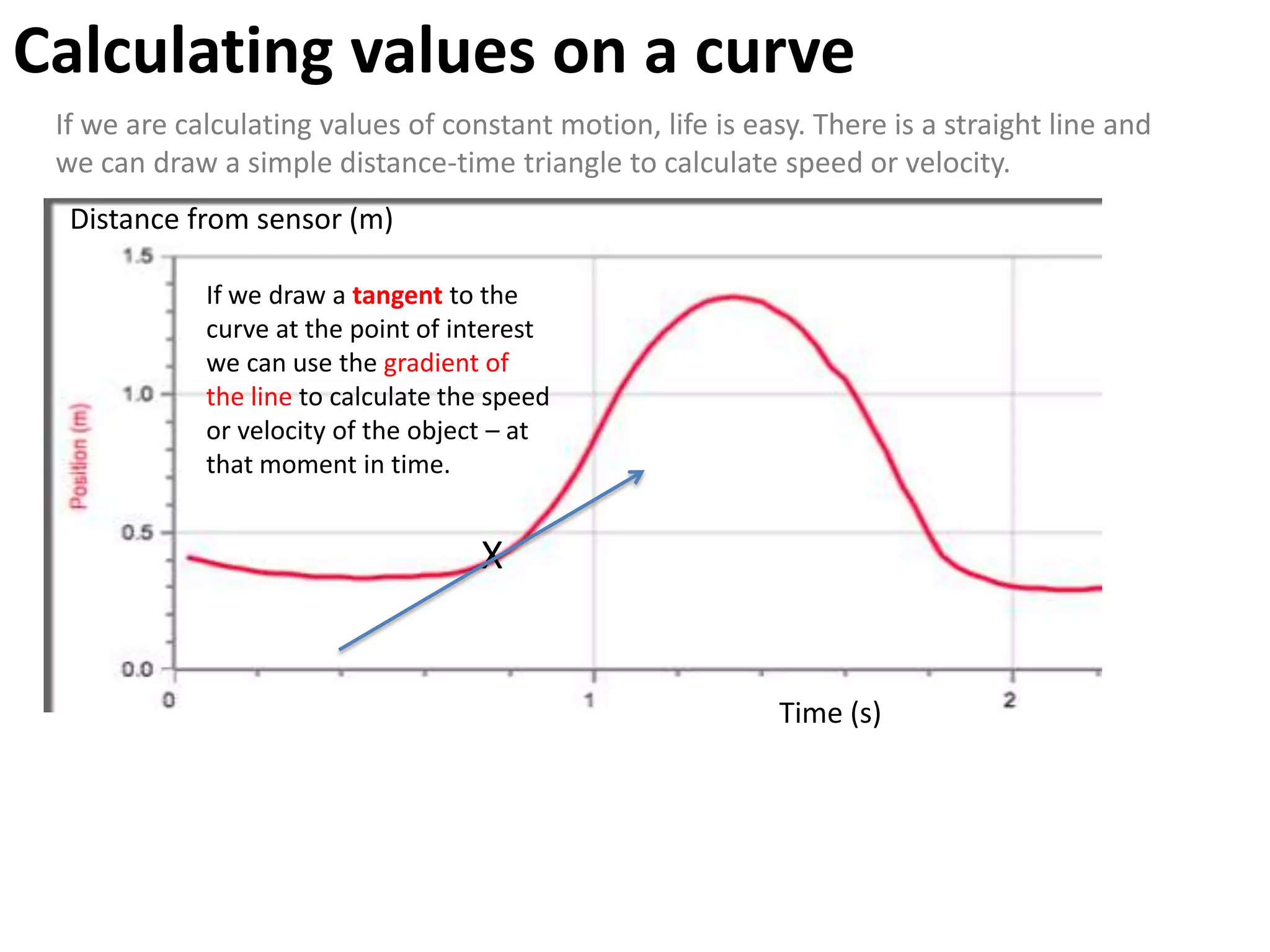
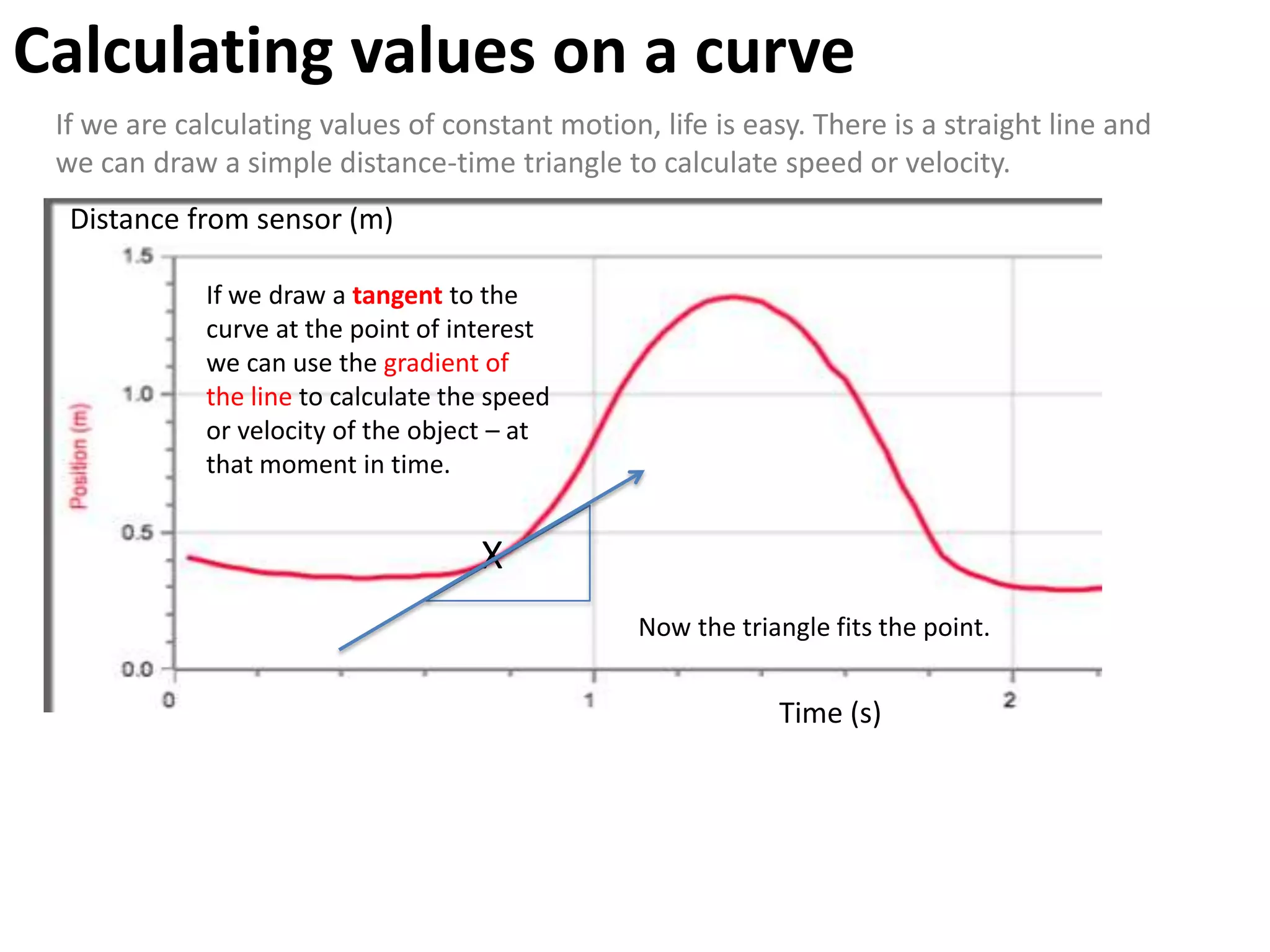
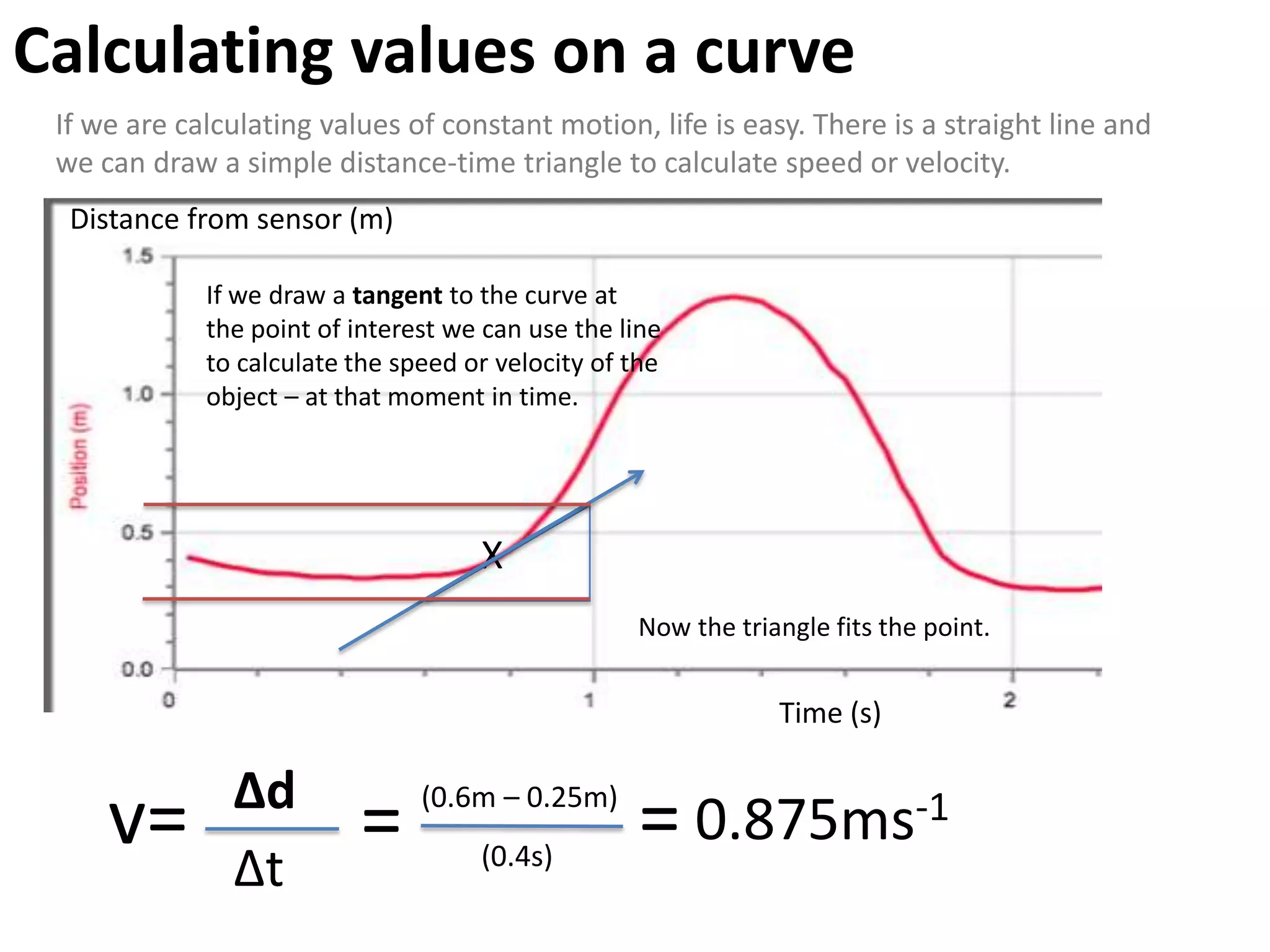
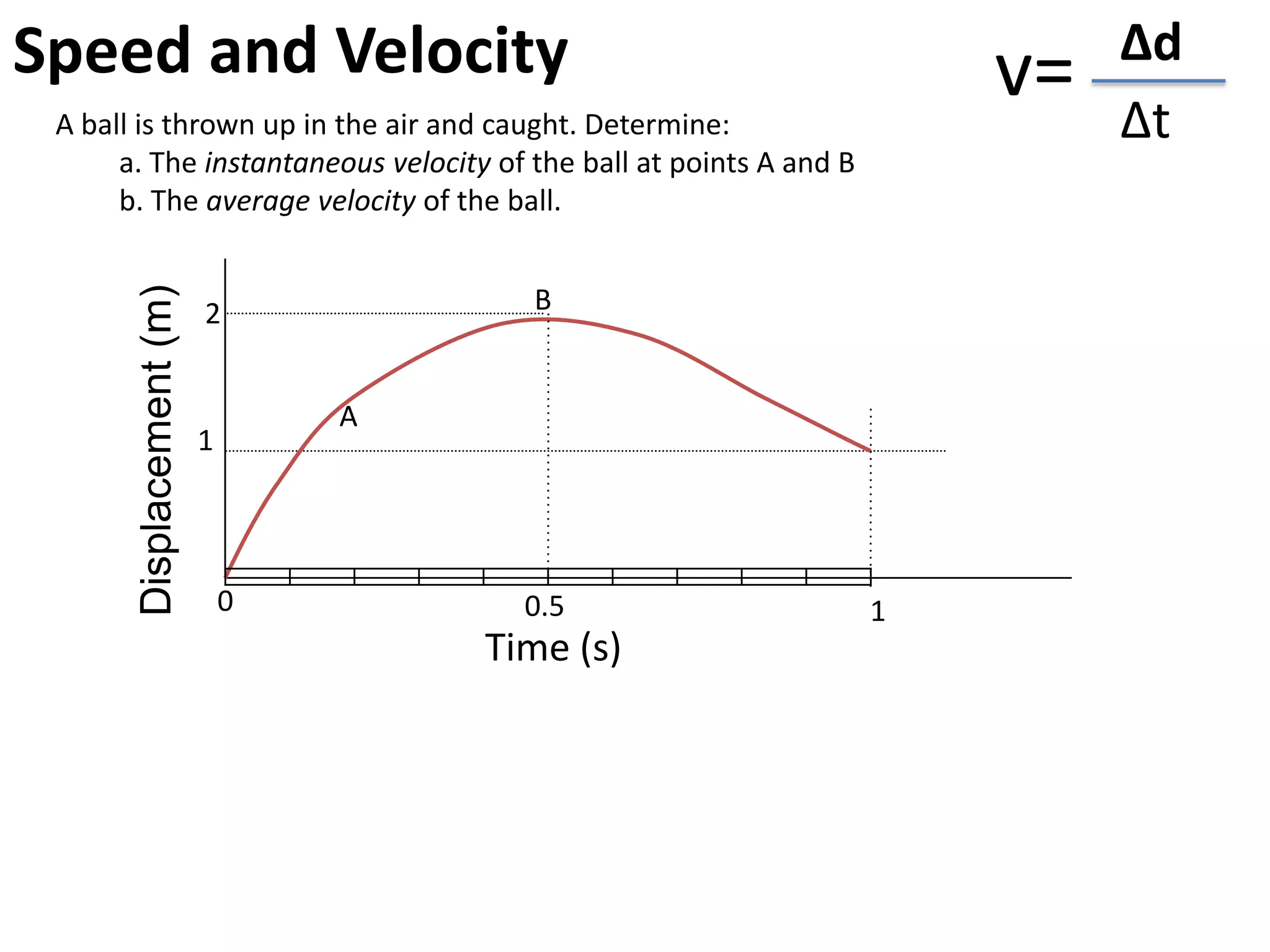
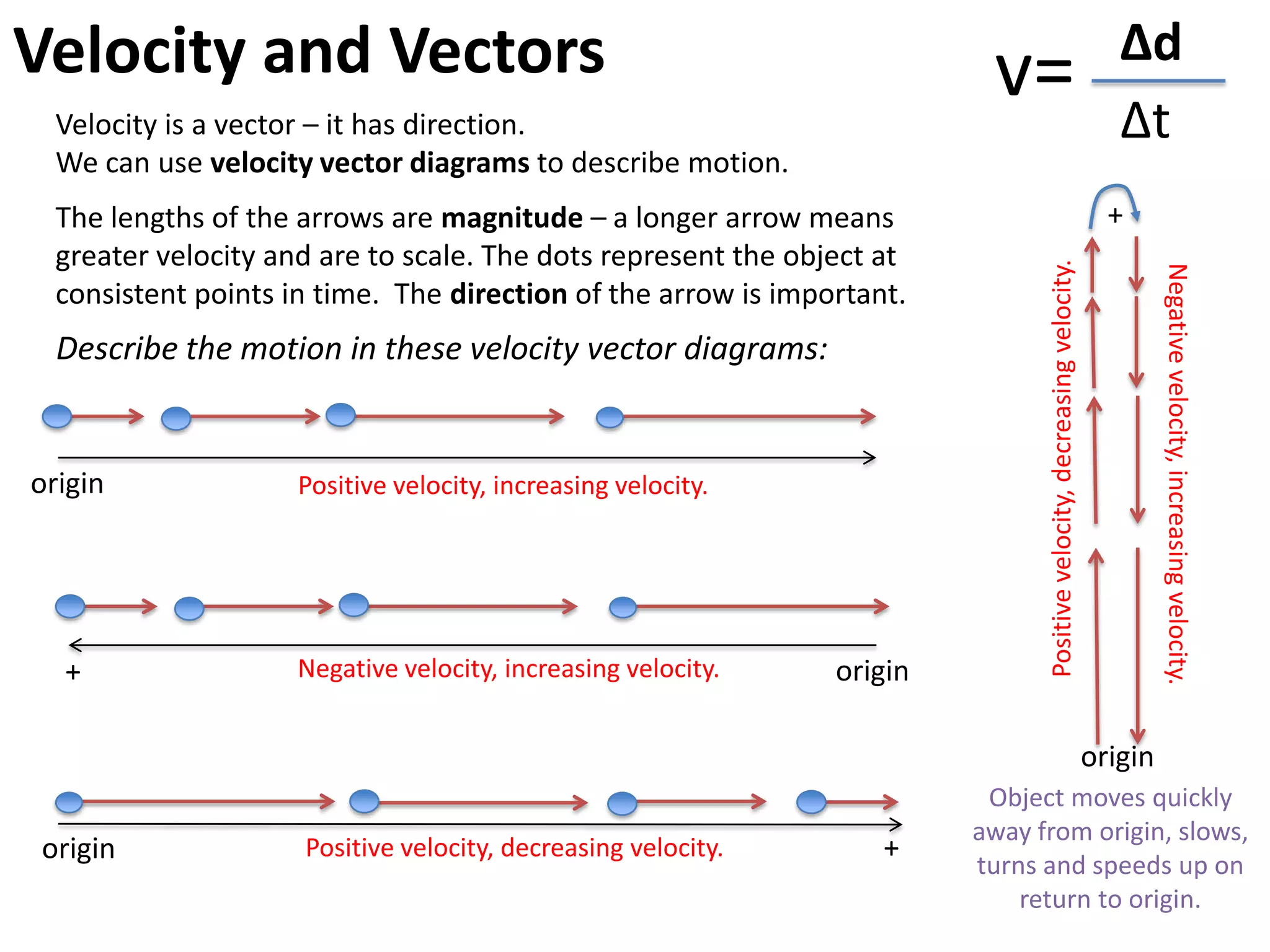
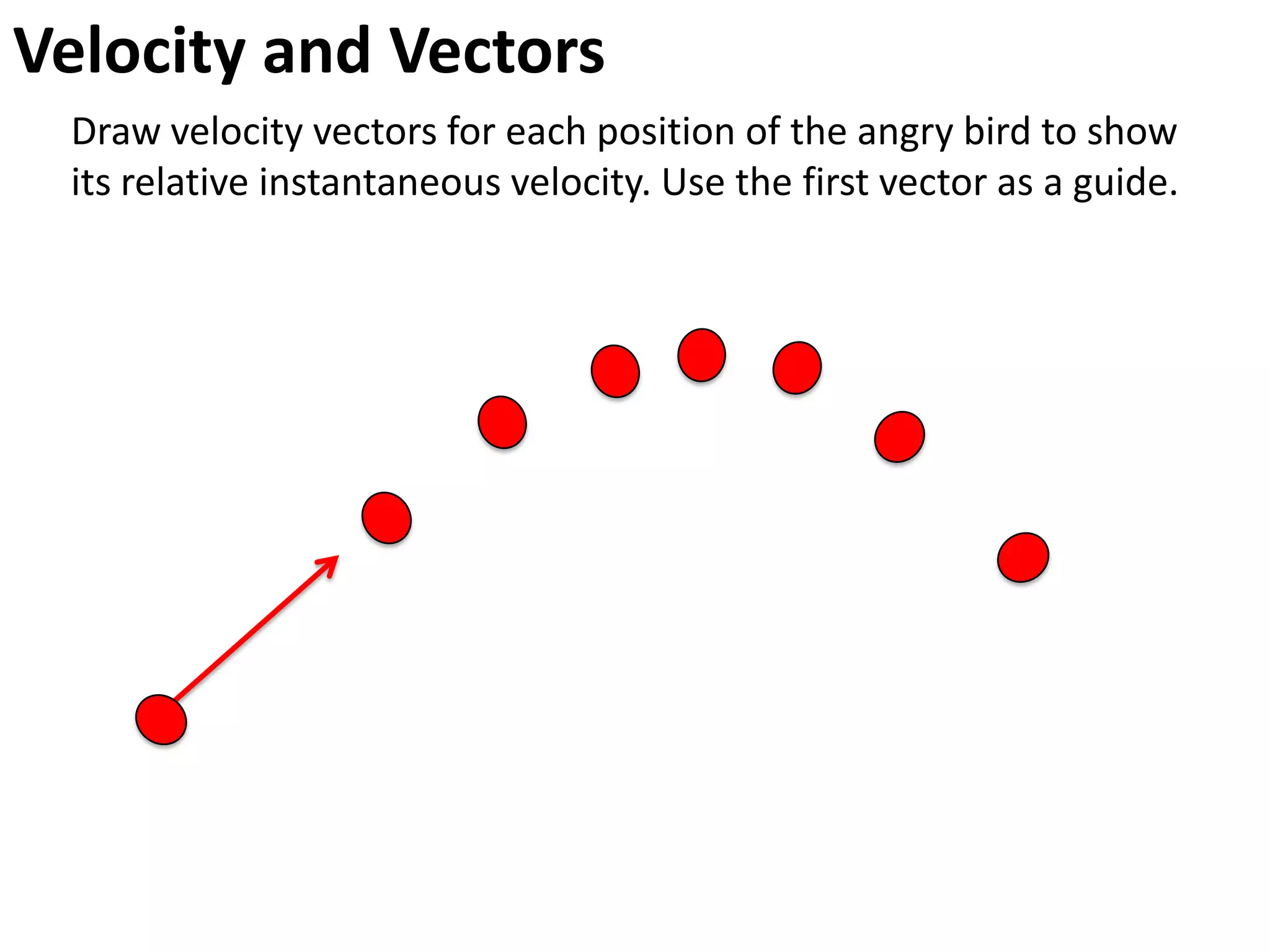
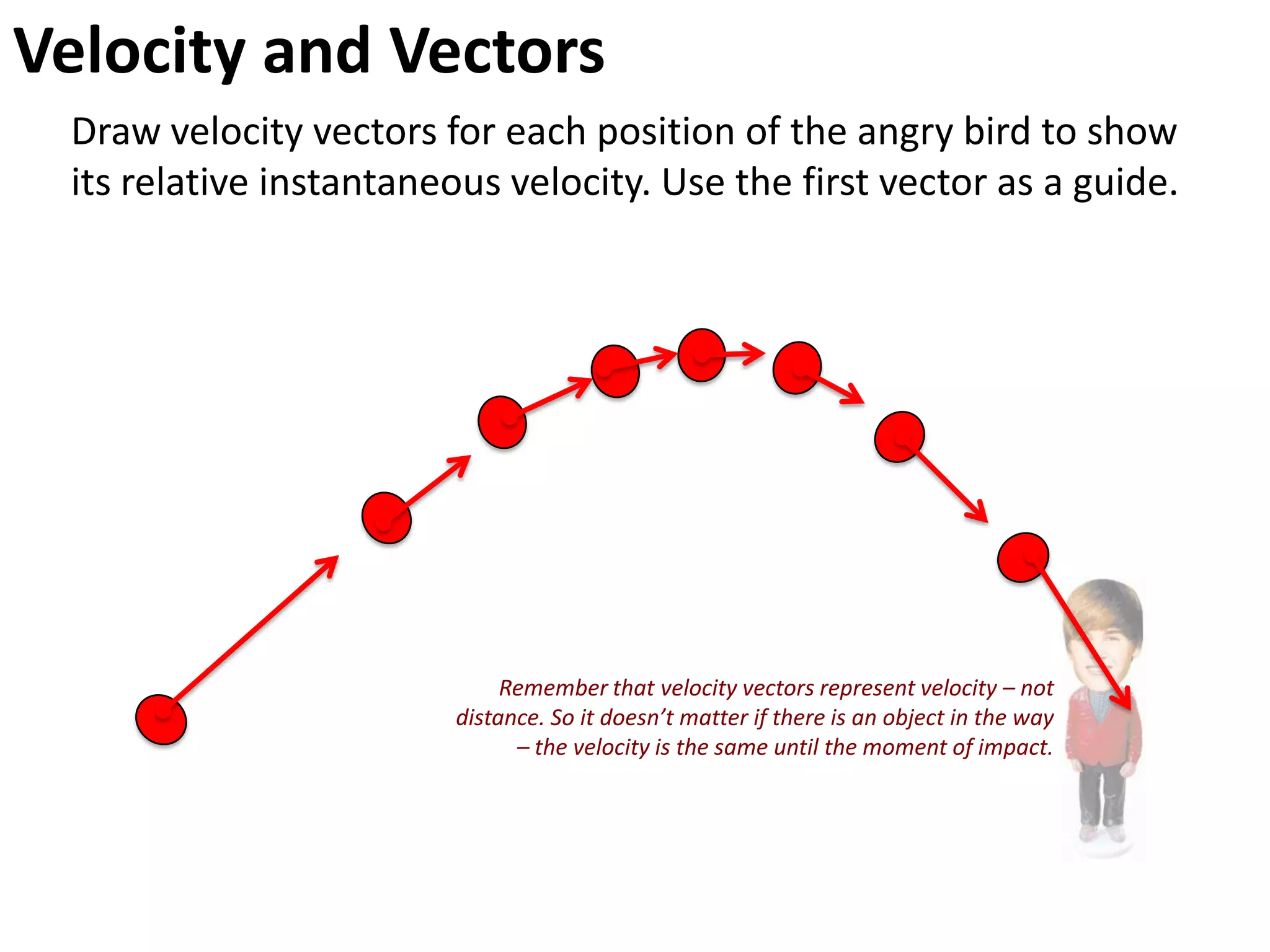
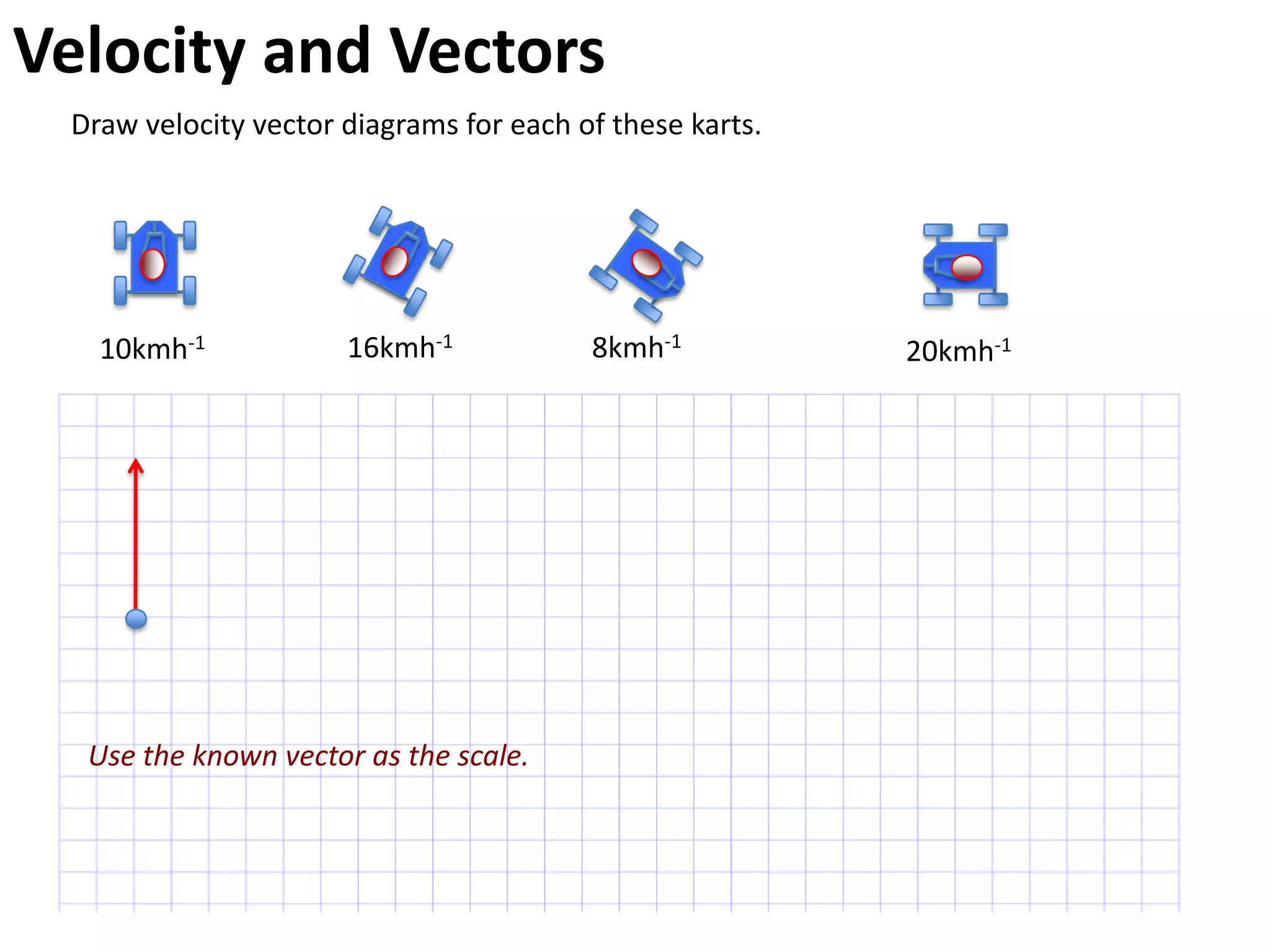
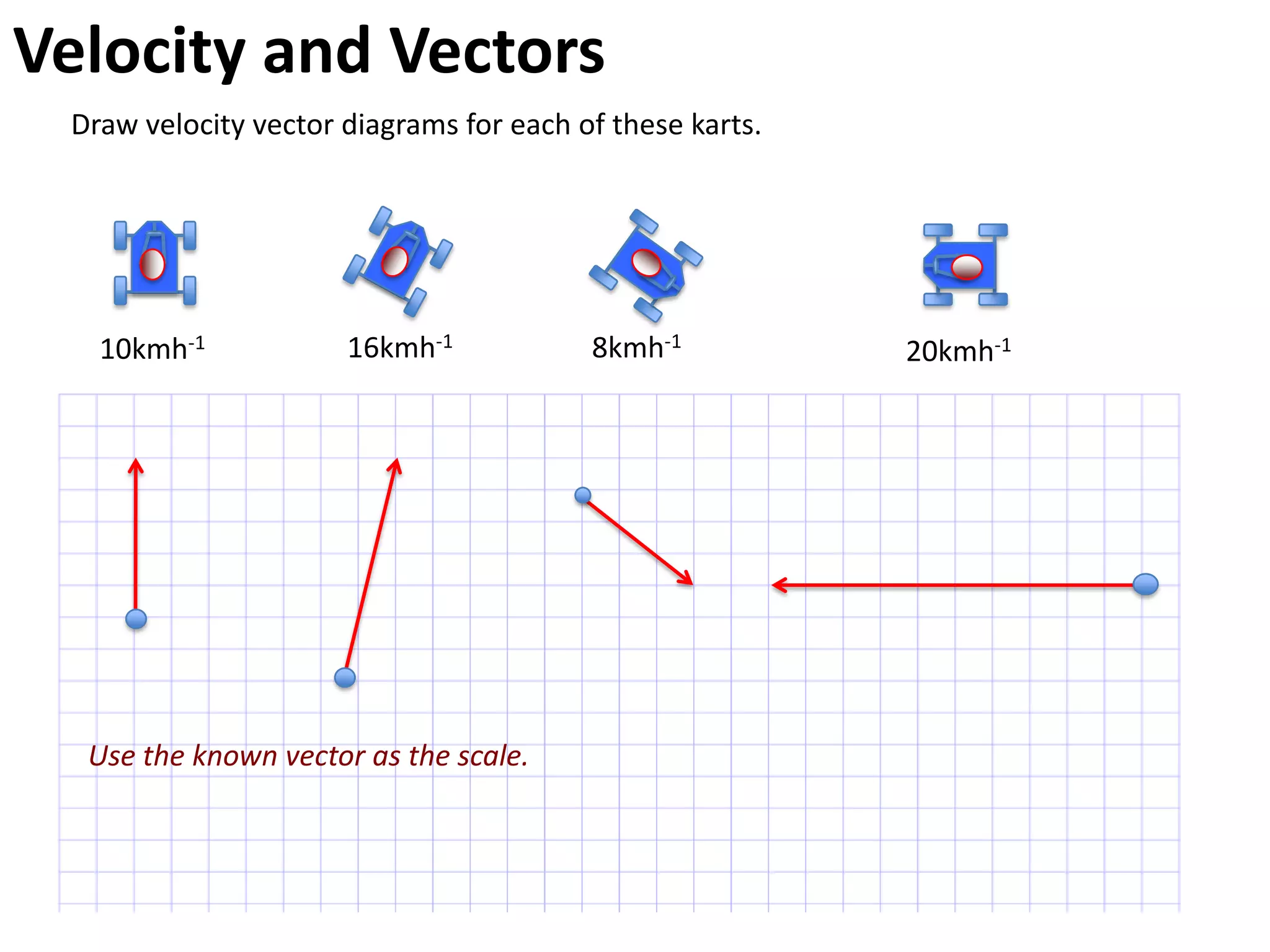
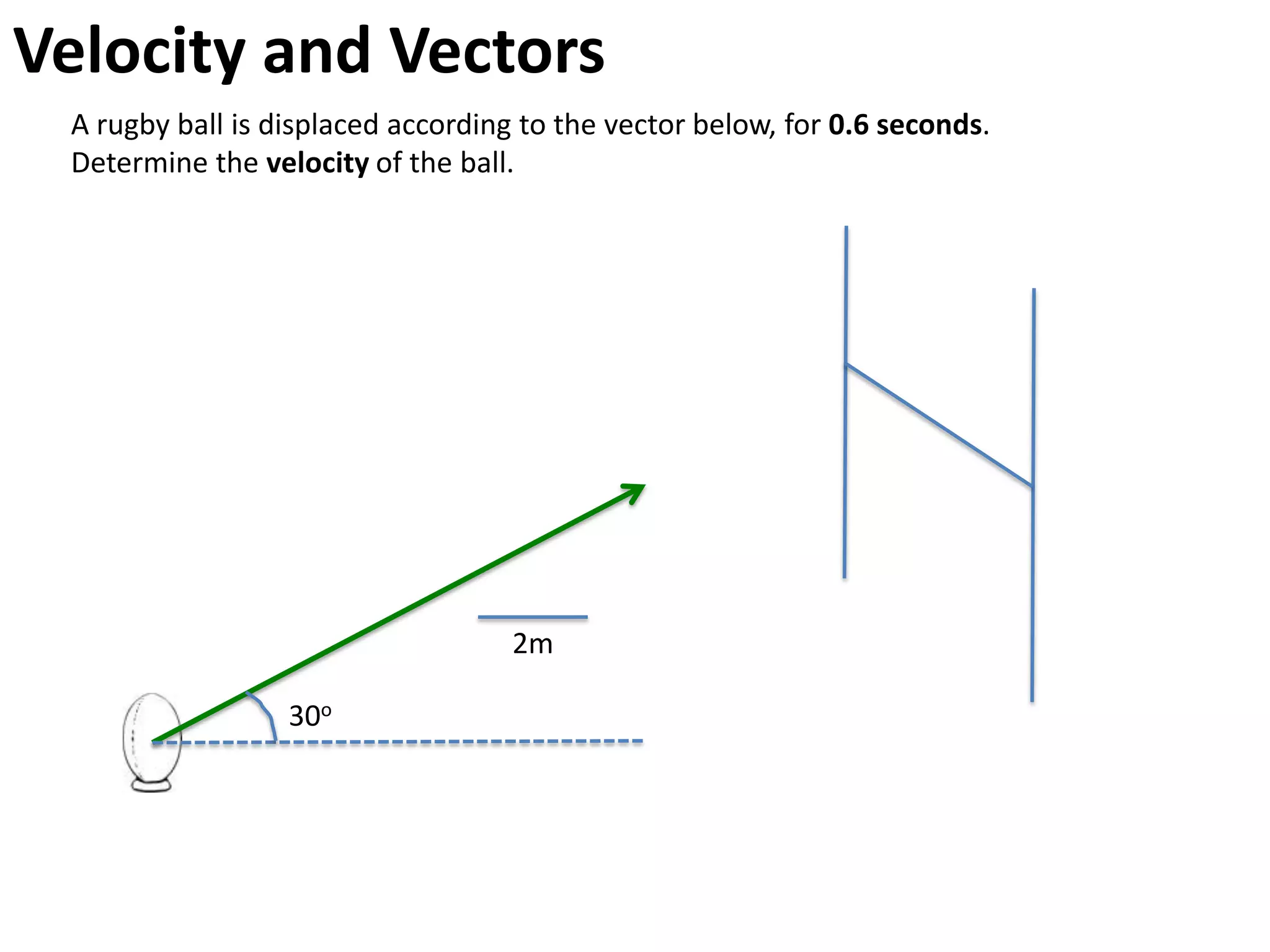
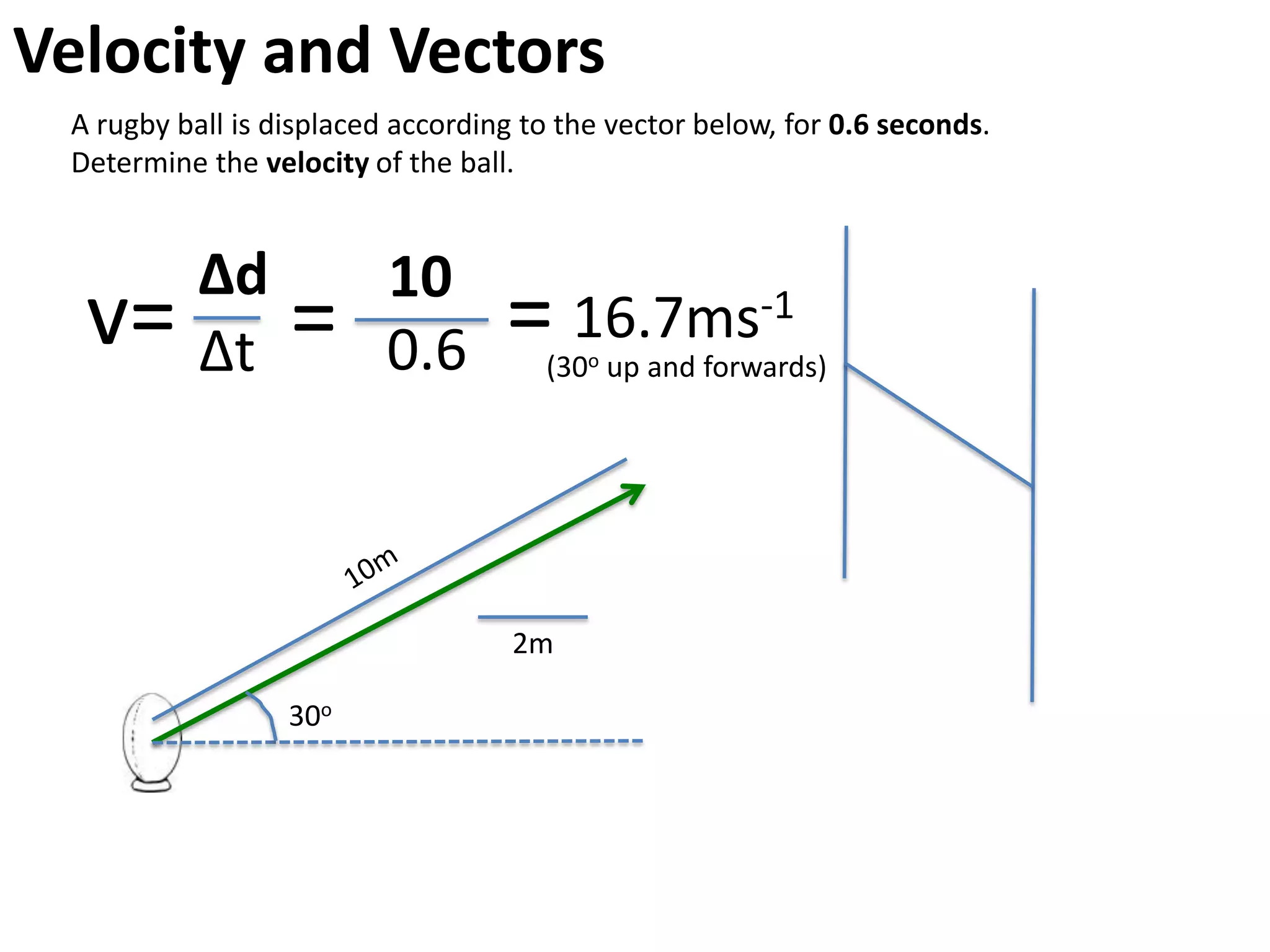
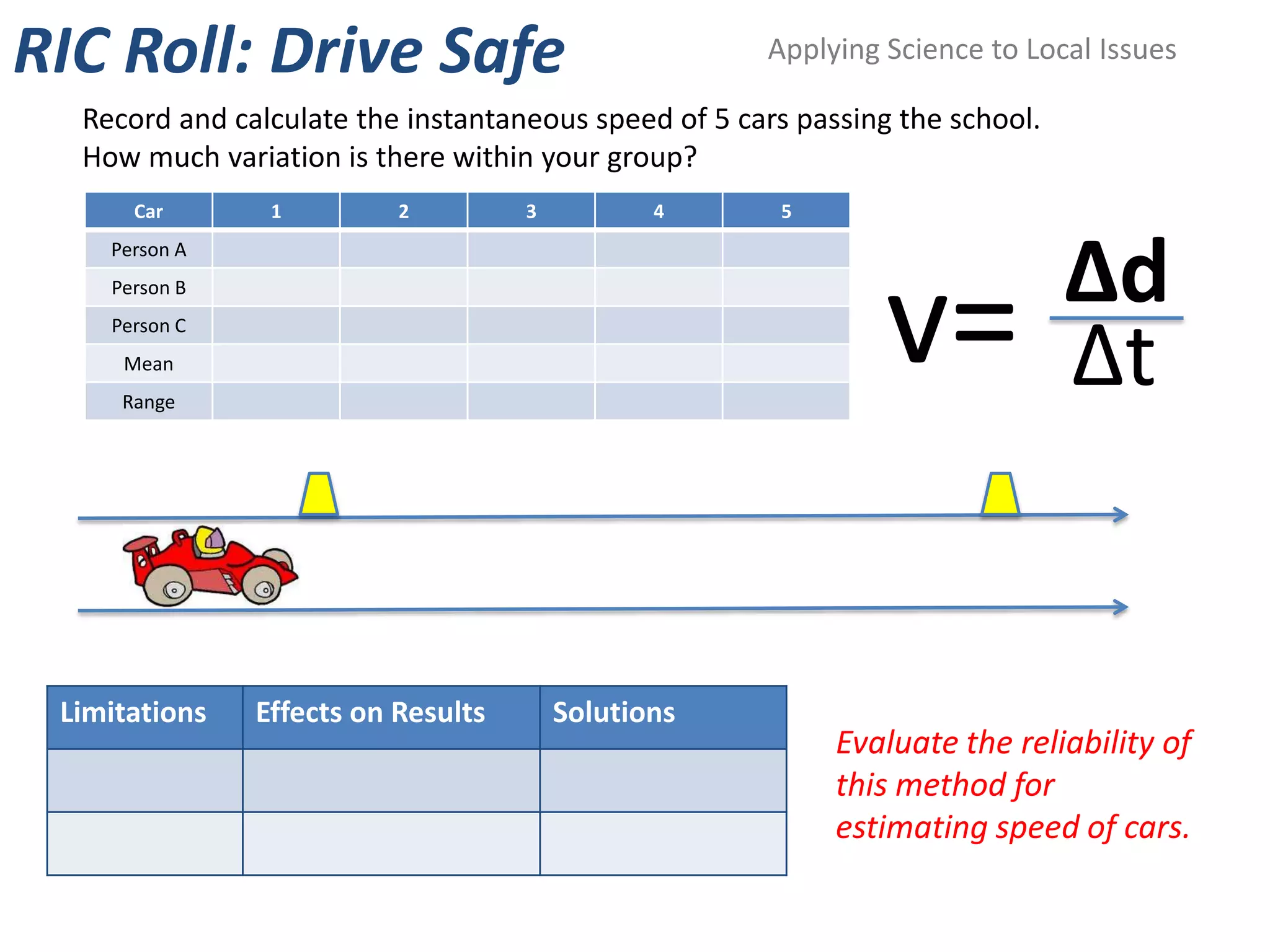
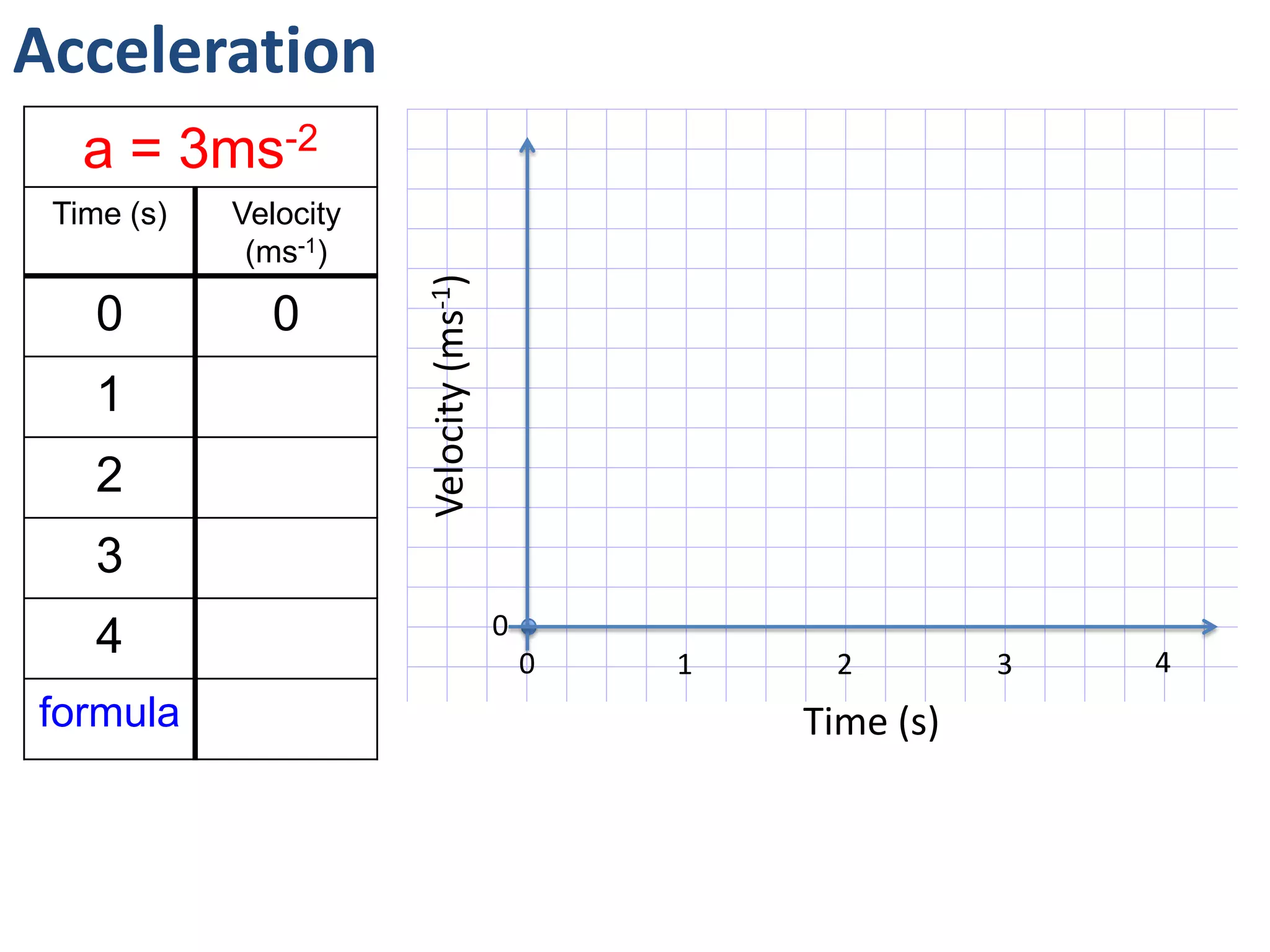
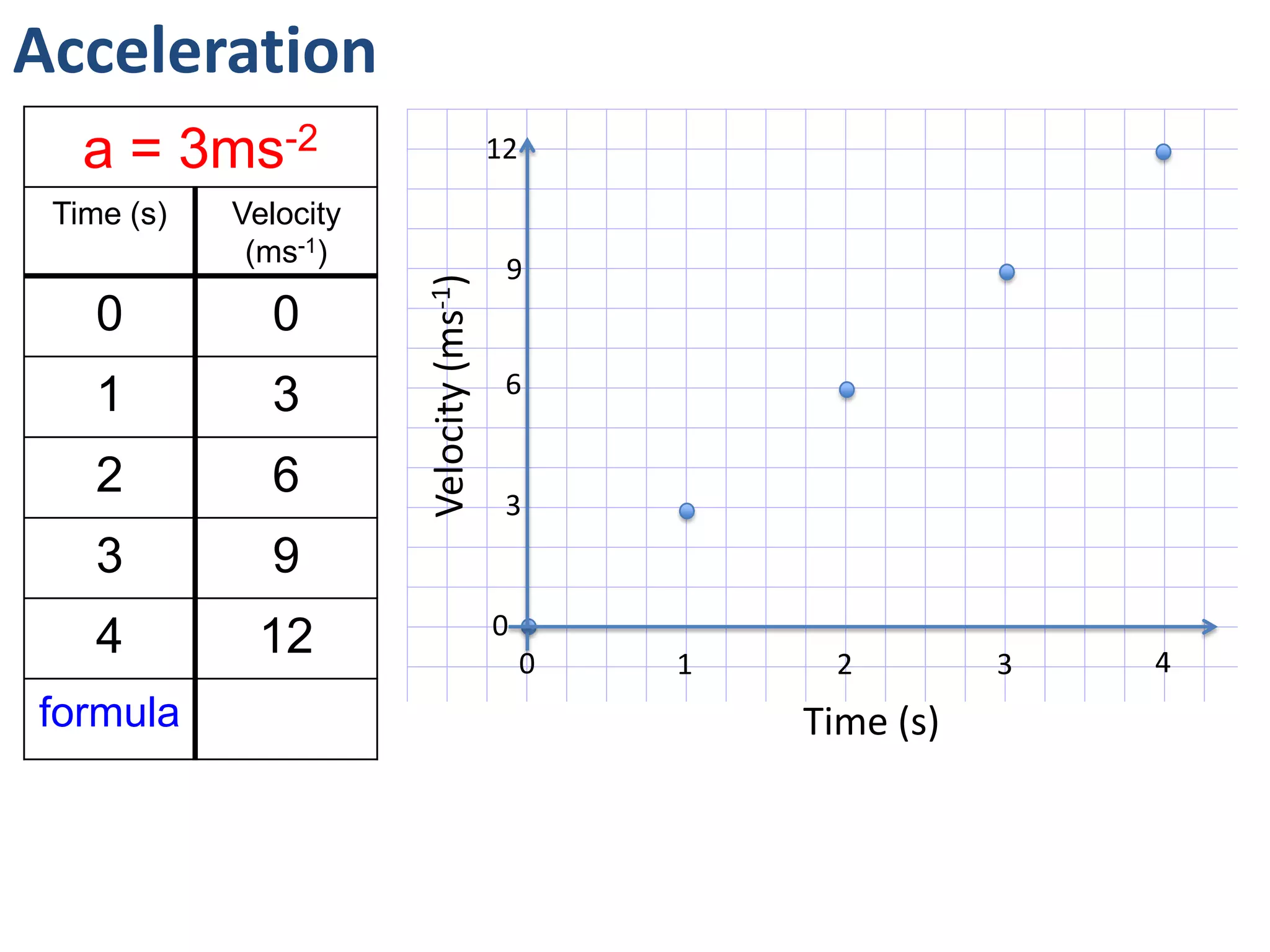
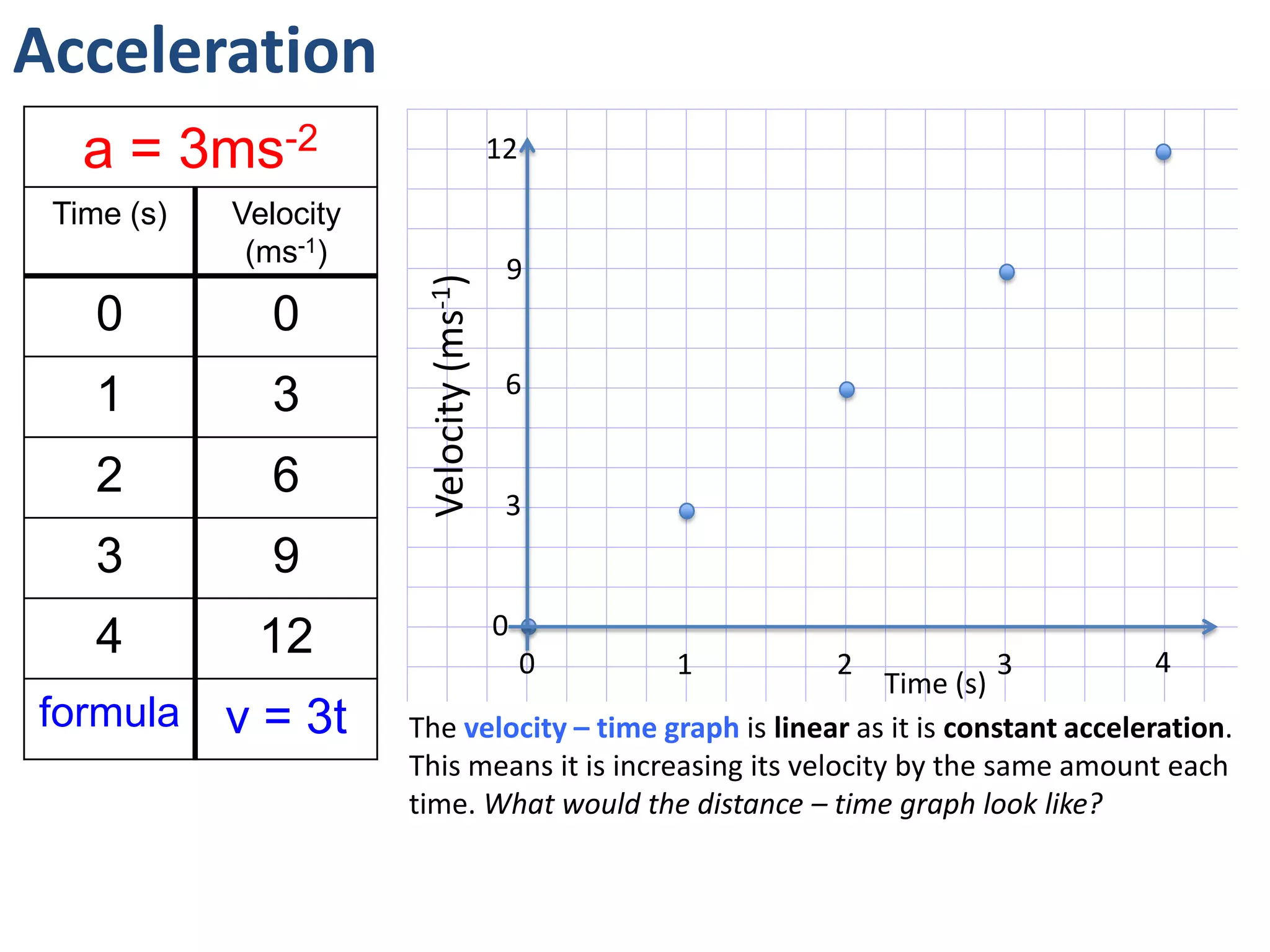
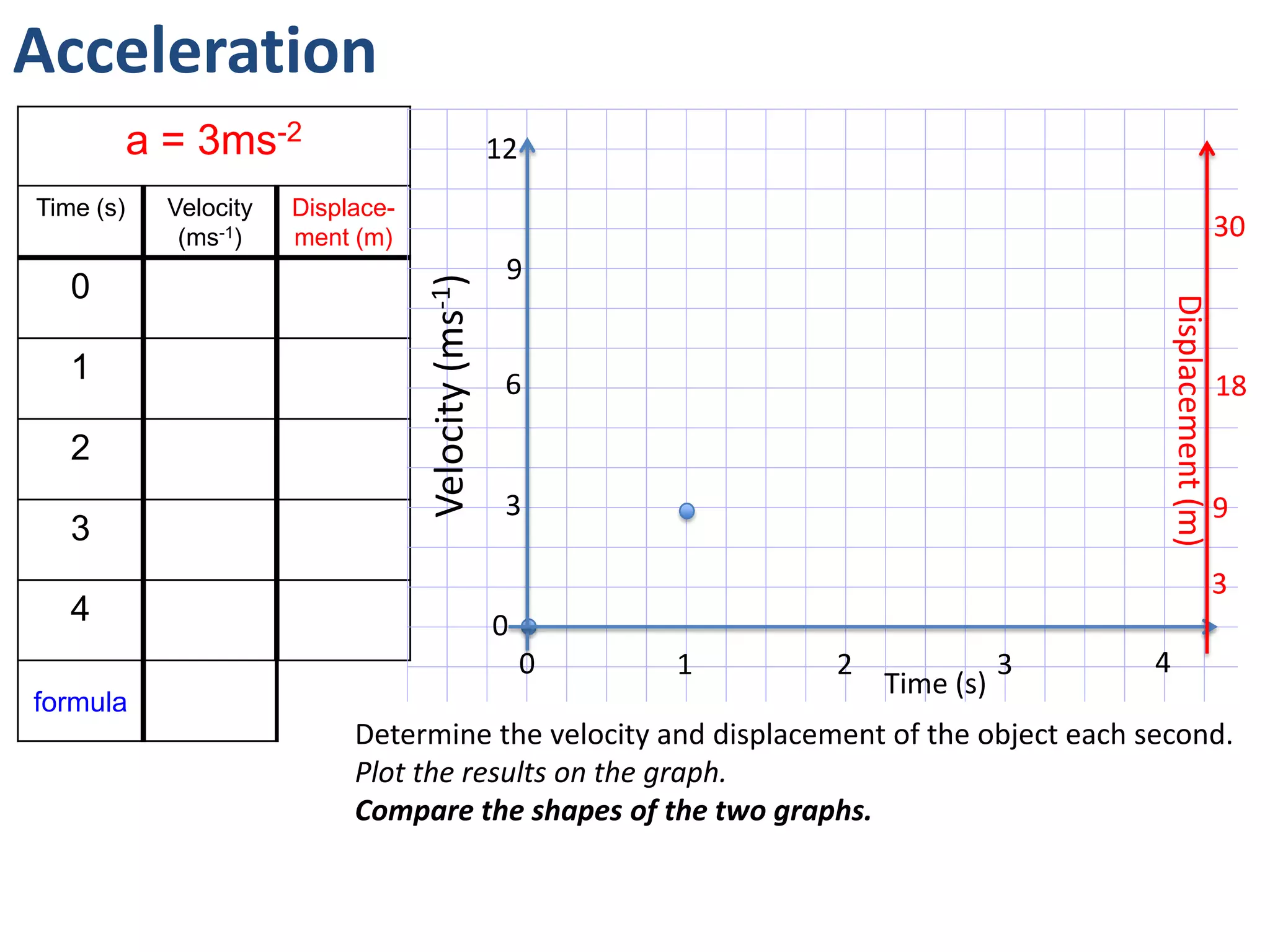
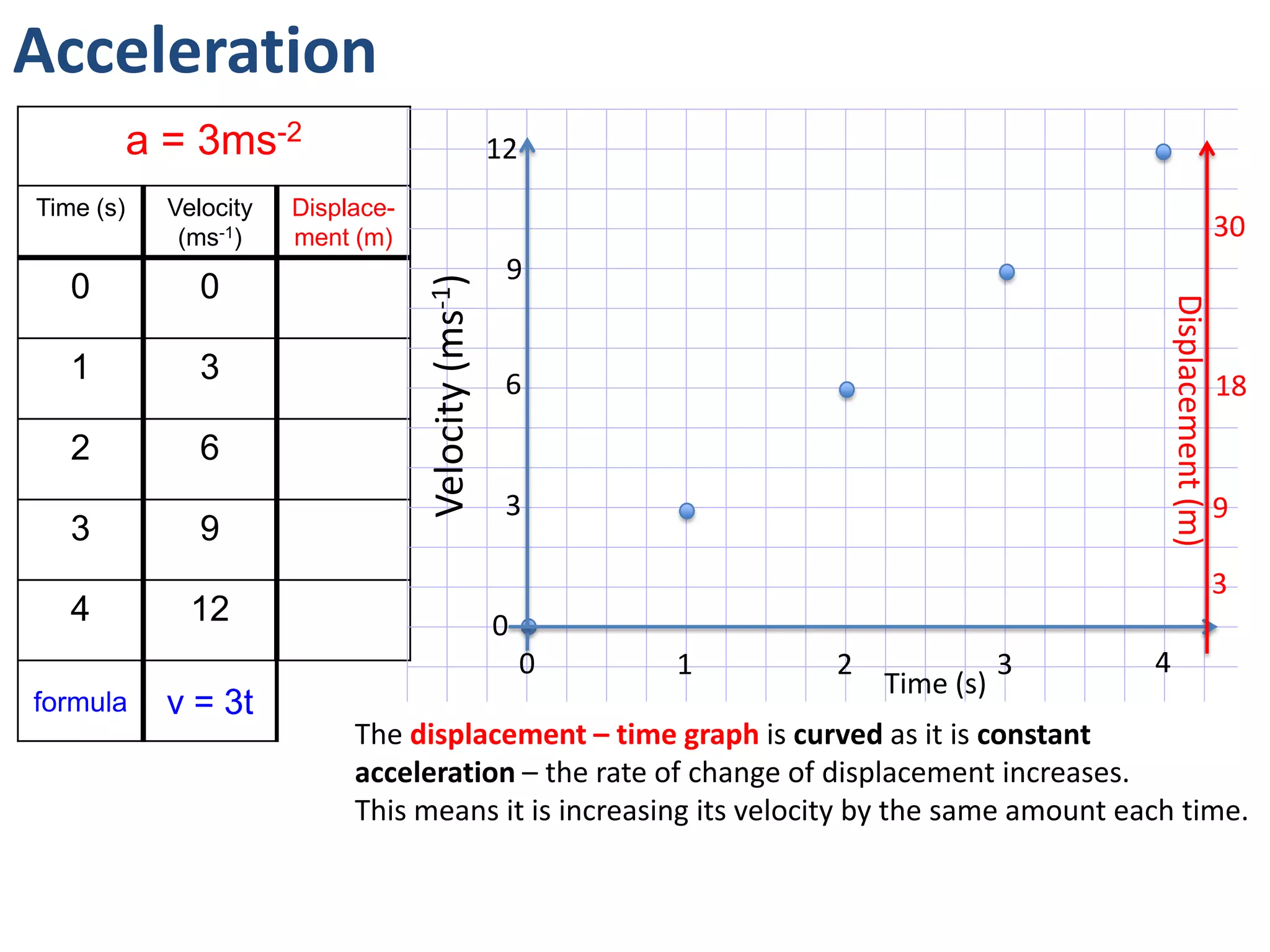
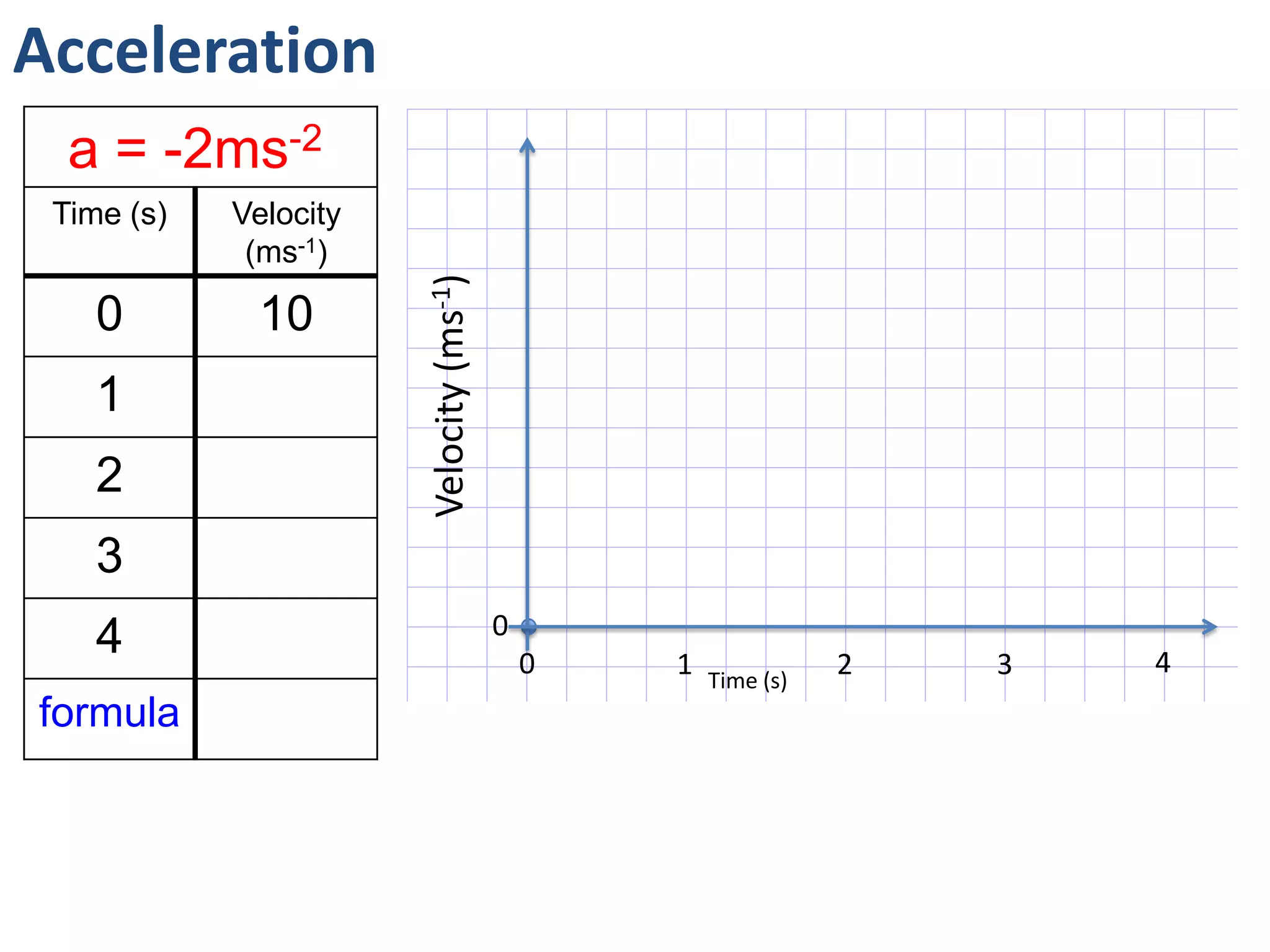
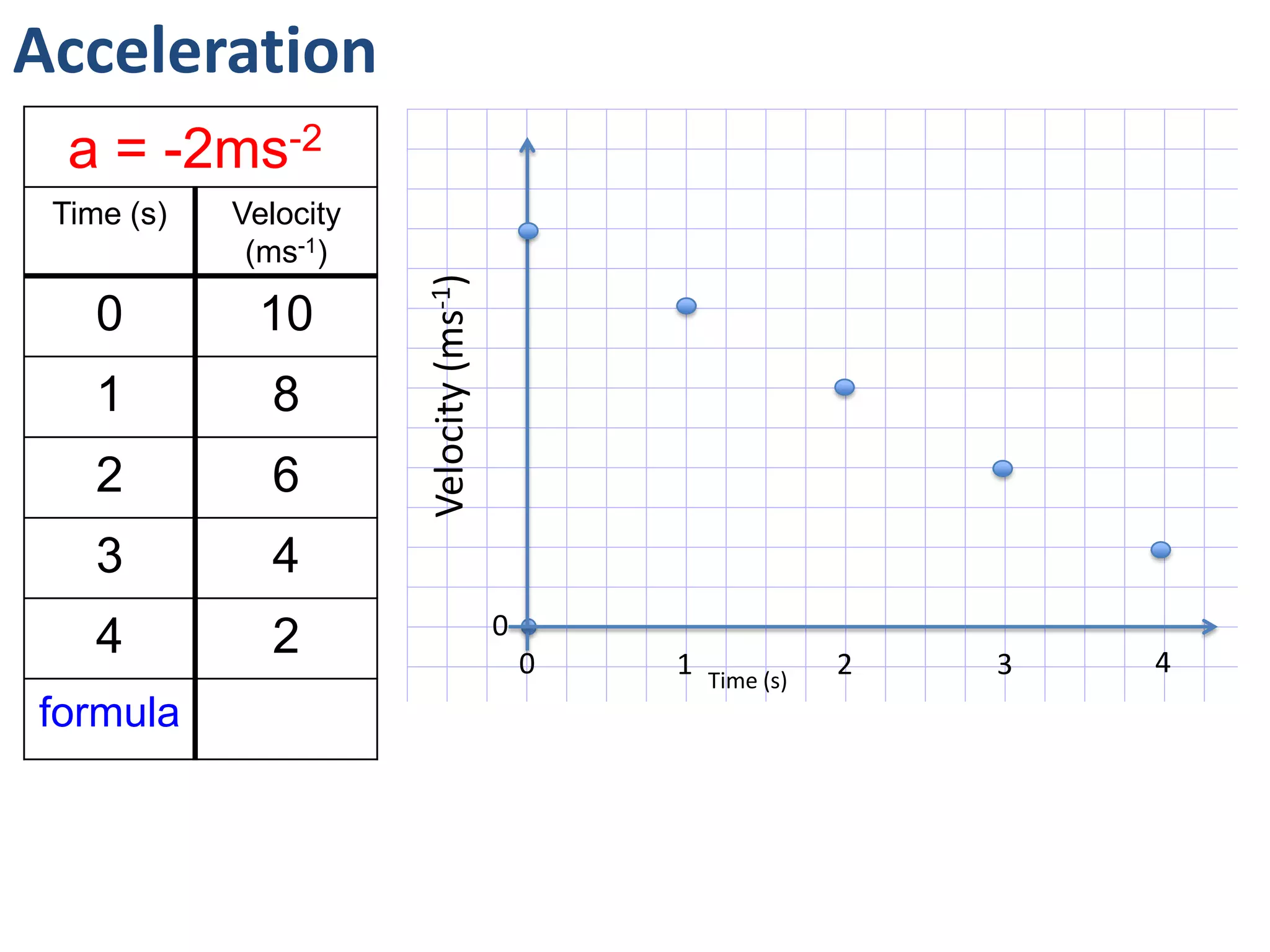
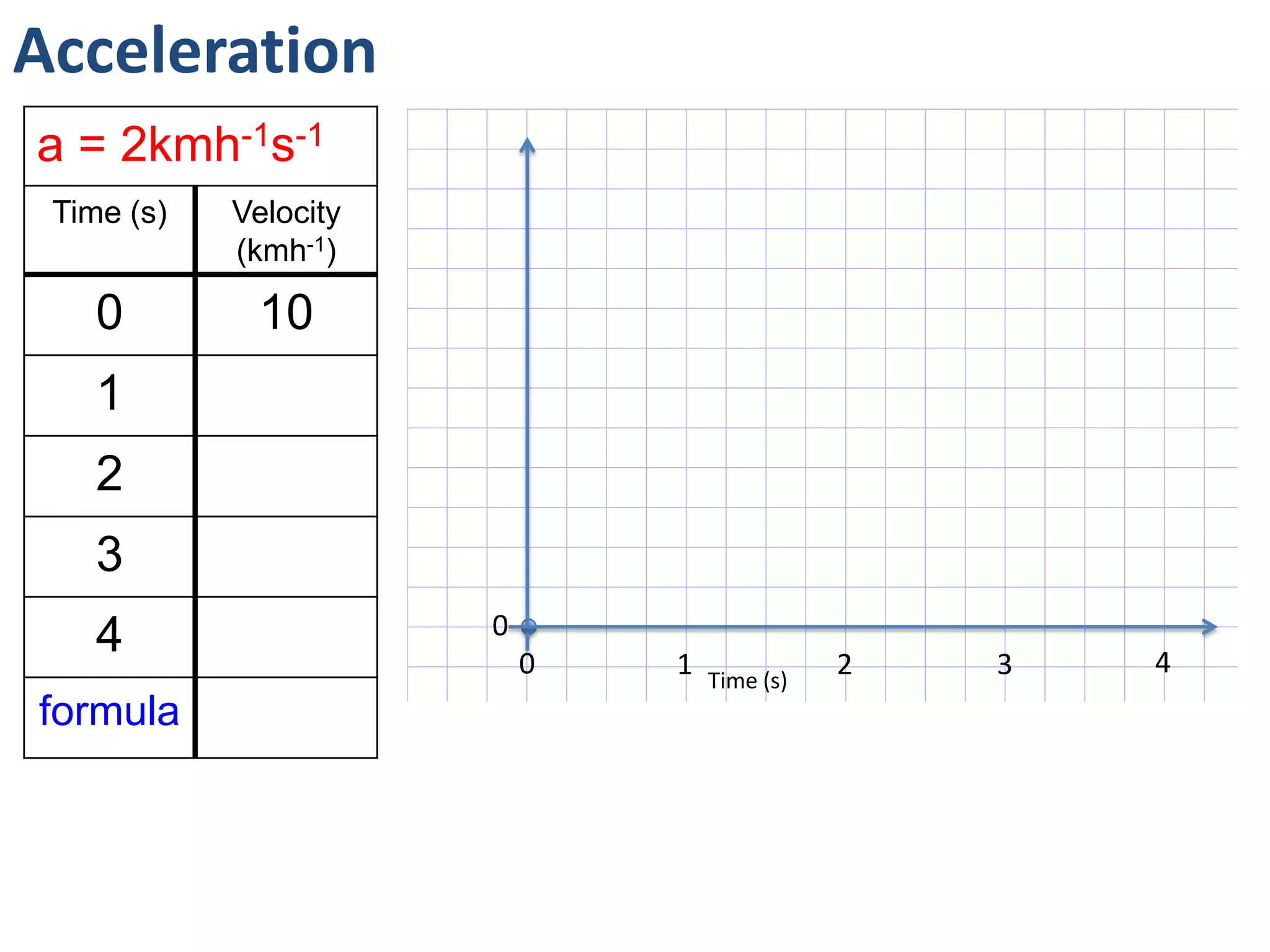
The document introduces kinematics, which is the science of describing motion through graphical representations, calculations, and diagrams. It differentiates between distance (a scalar) and displacement (a vector), emphasizing their significance in analyzing movement and plotting graphs of various motion scenarios. Additionally, the document outlines methods to calculate speed and velocity, highlighting their directional properties and the importance of understanding changes in motion.