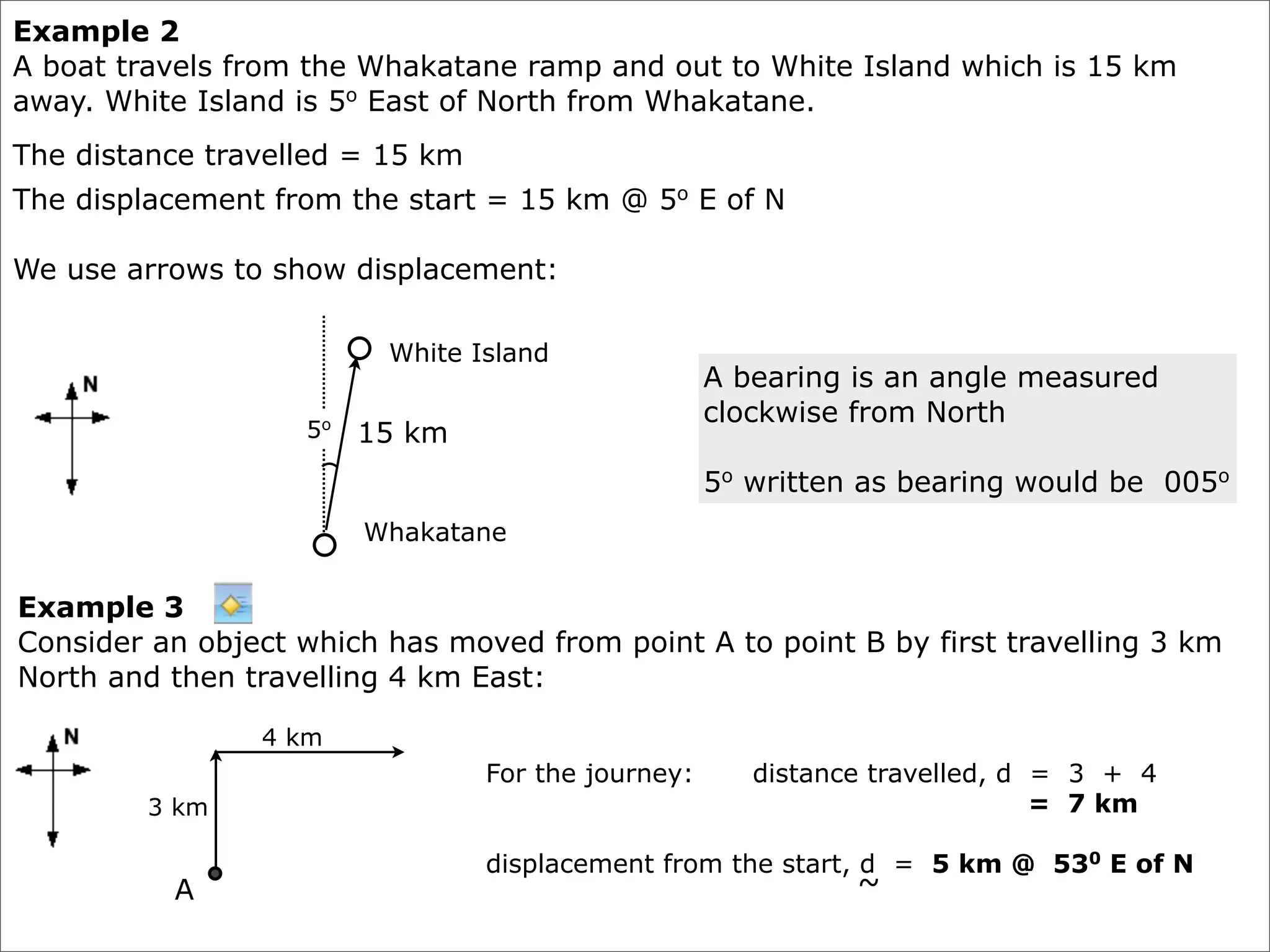
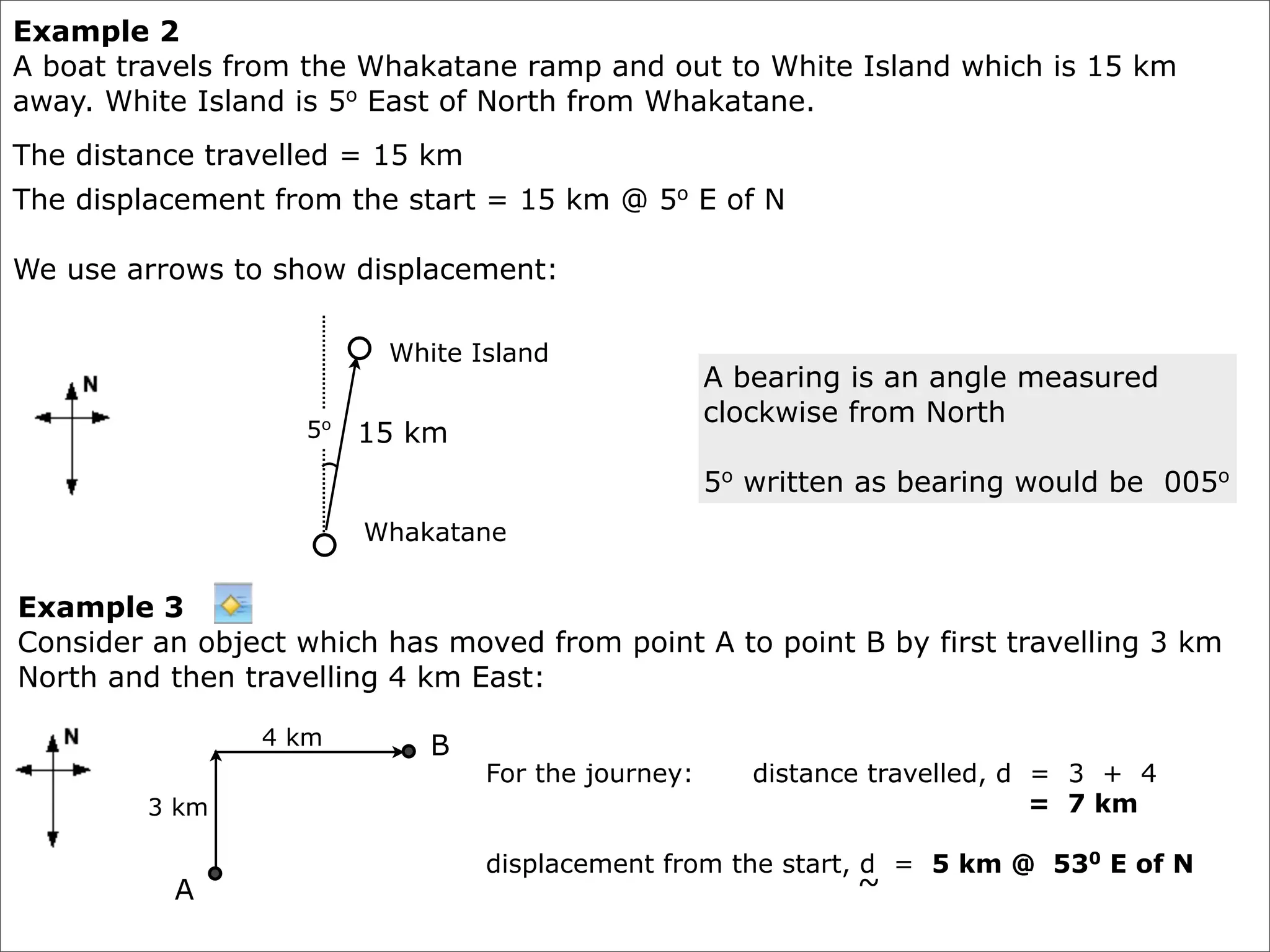
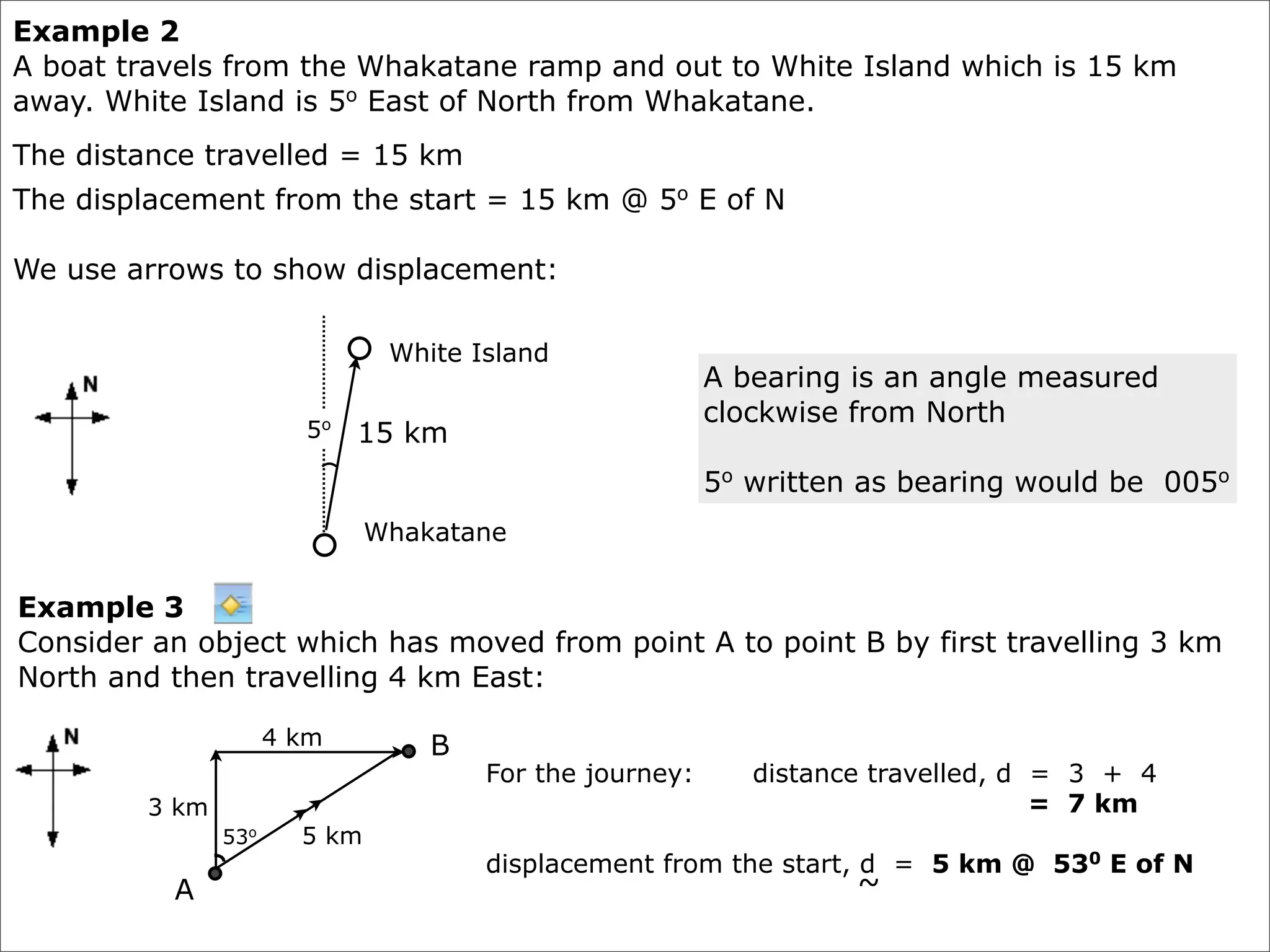
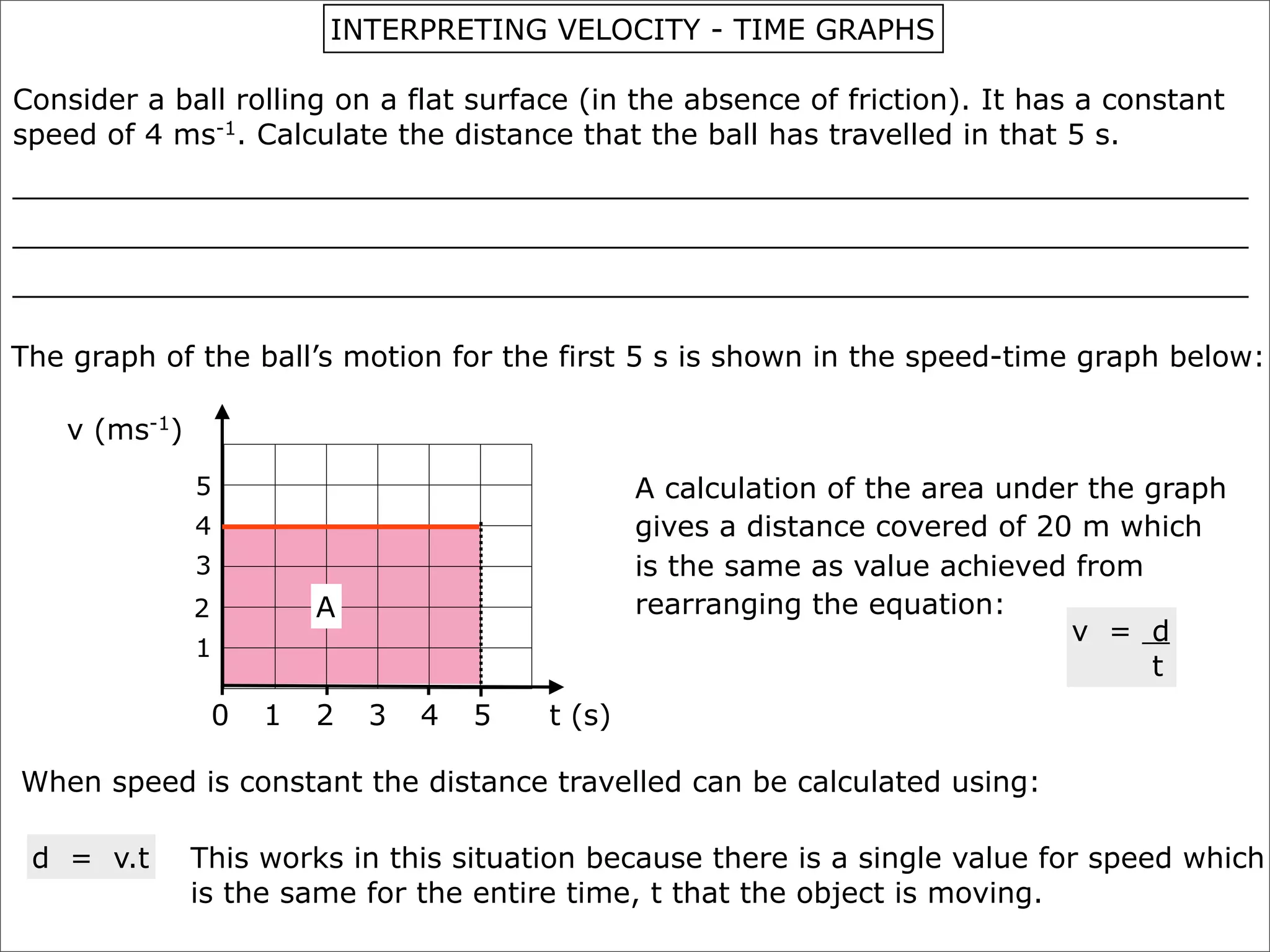
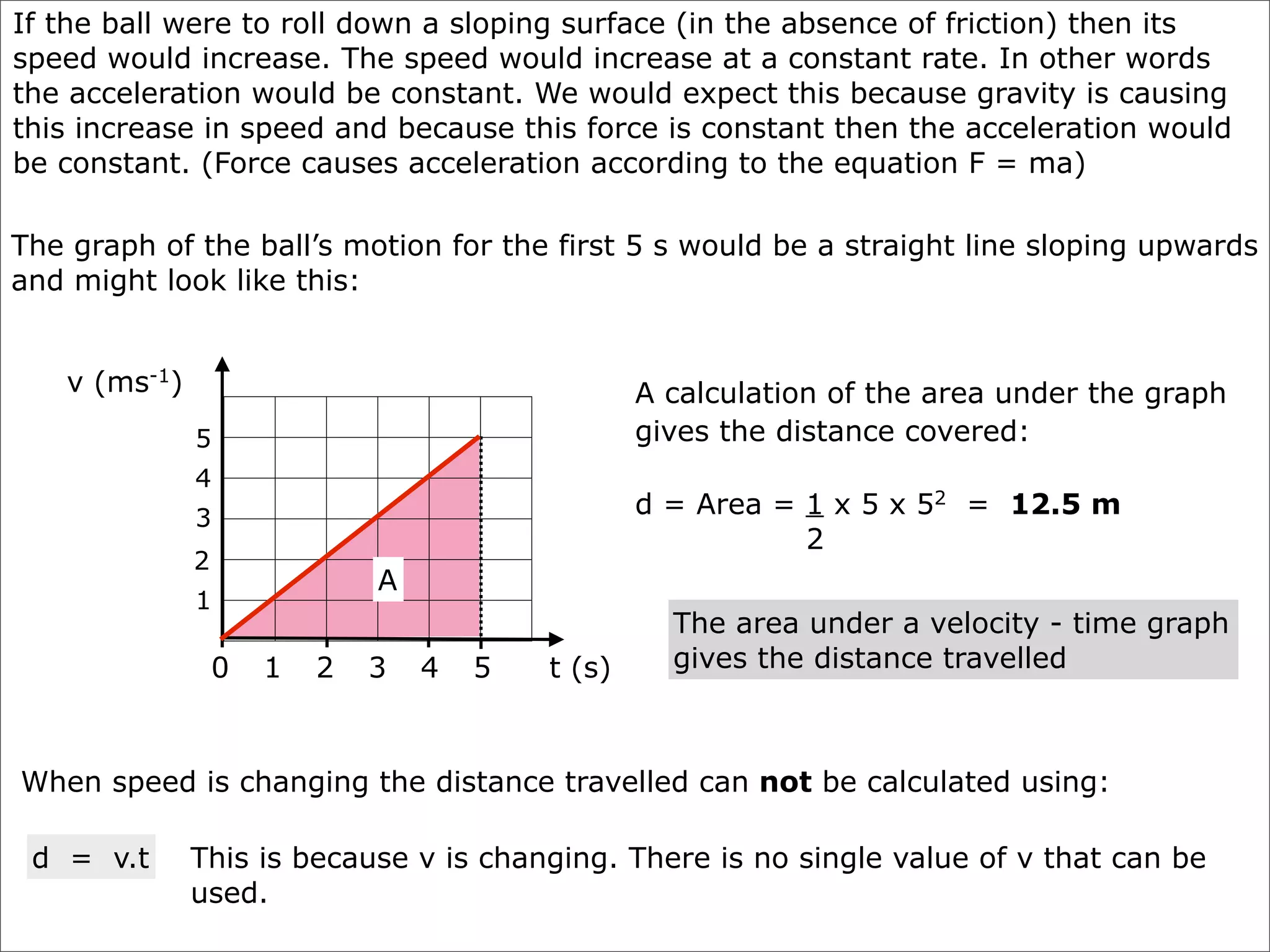
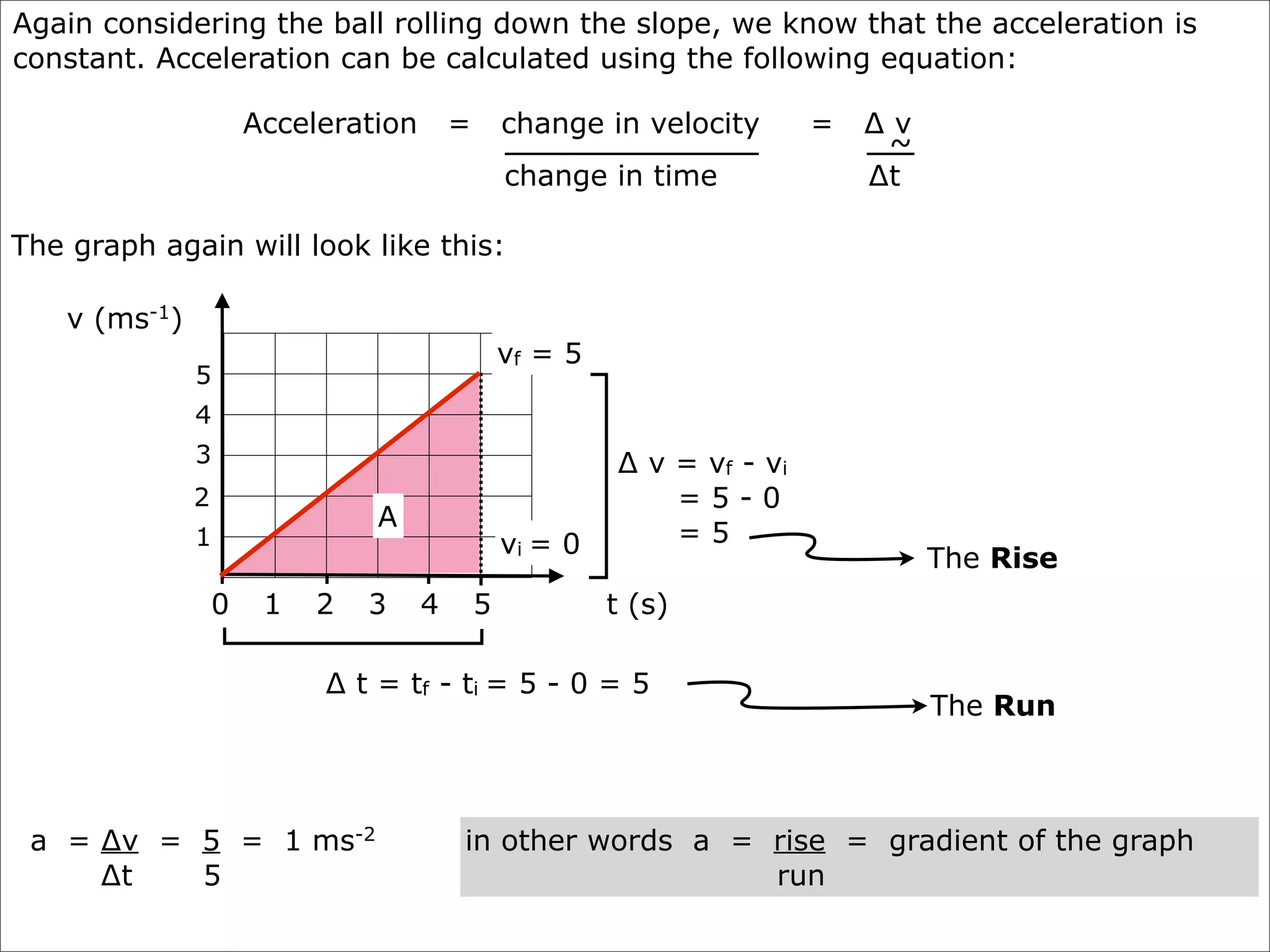
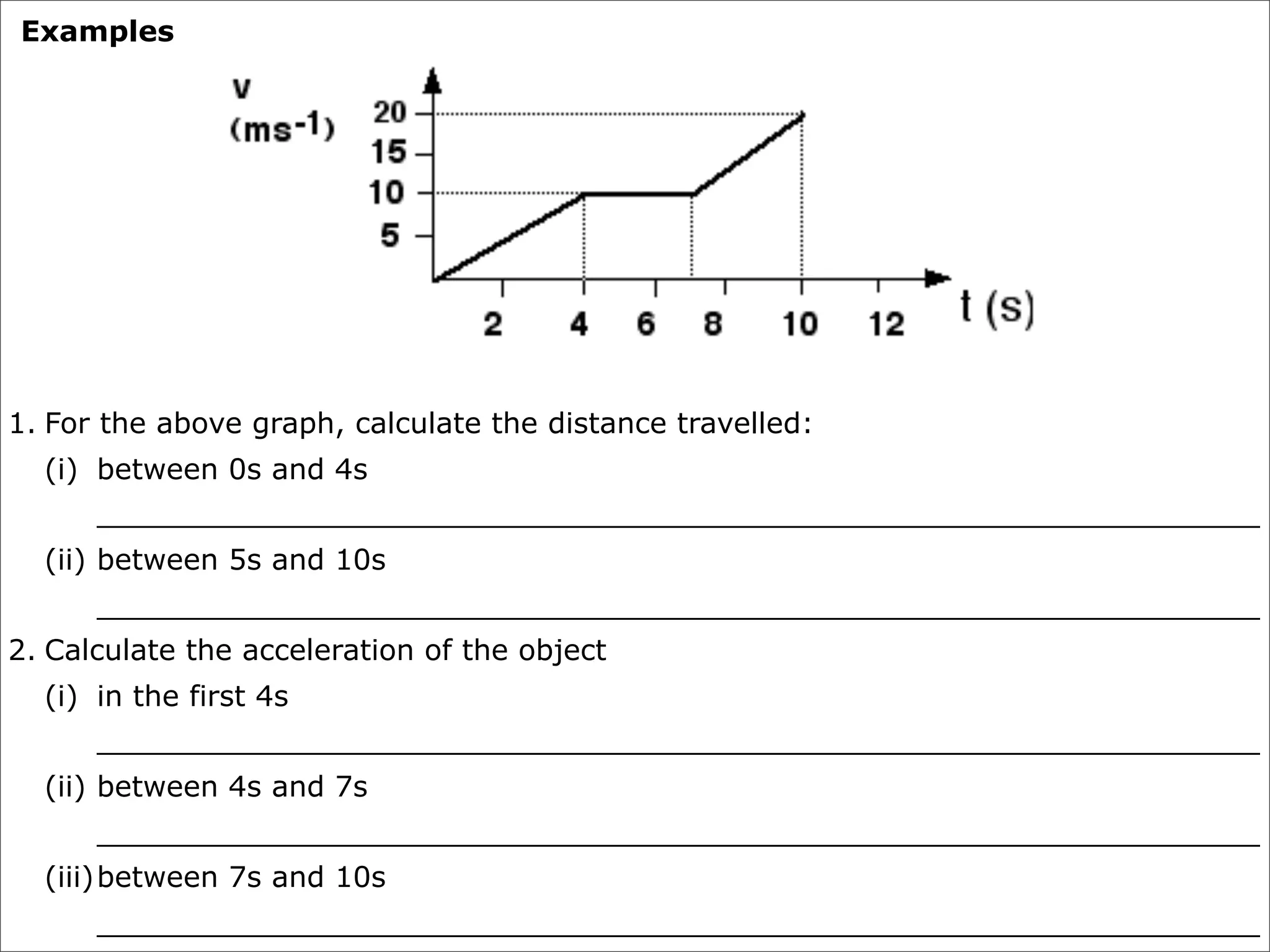
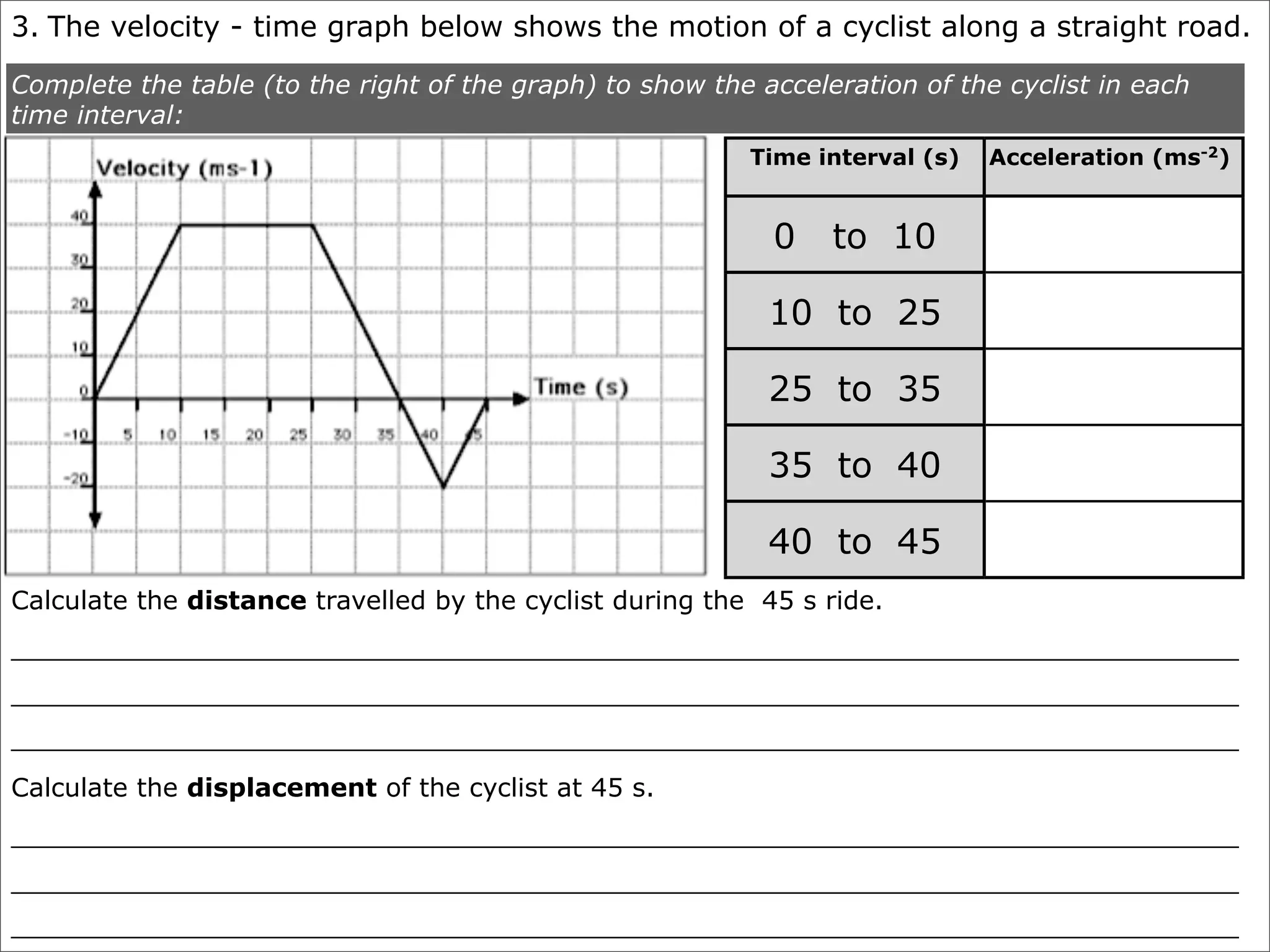
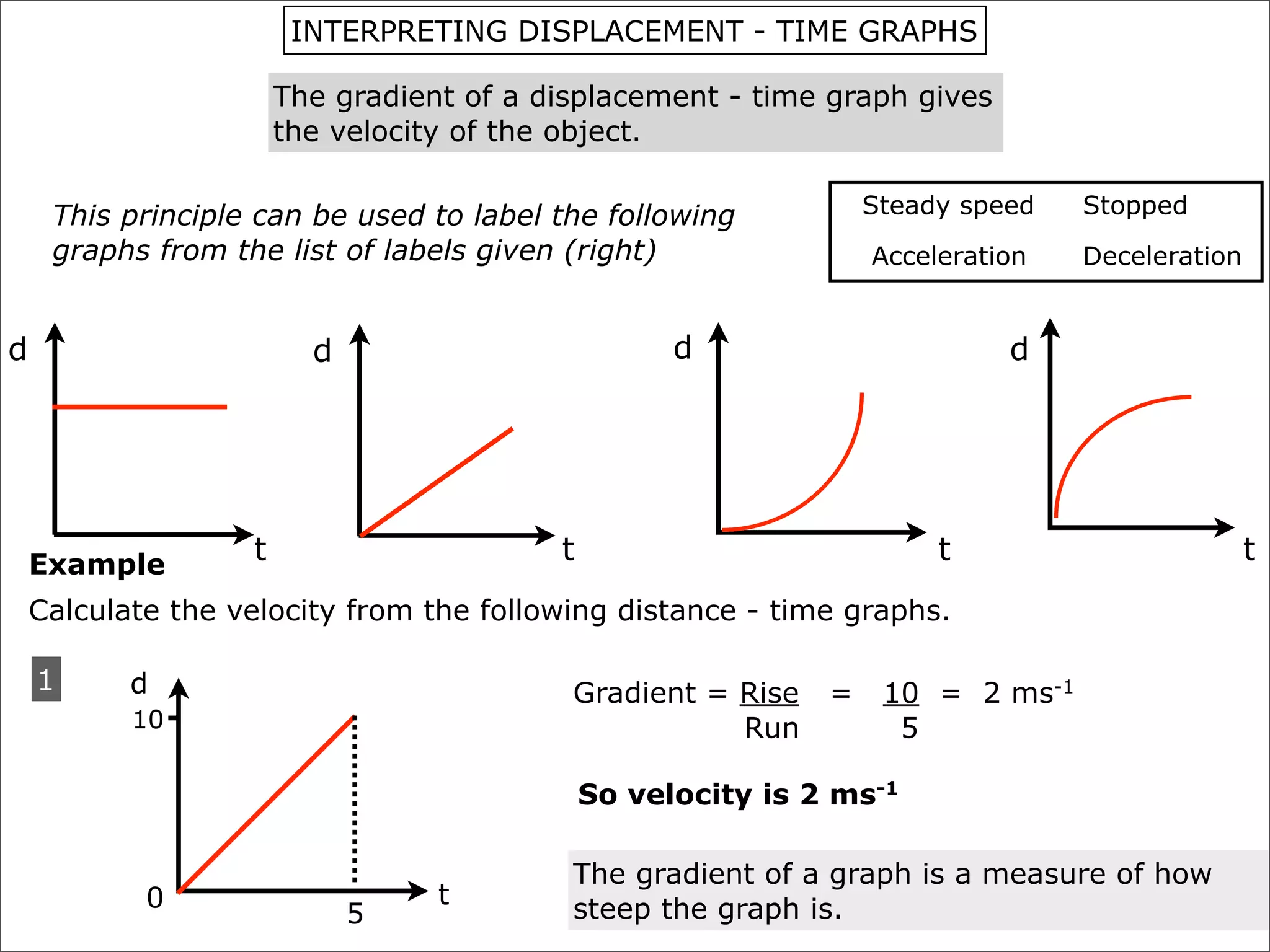
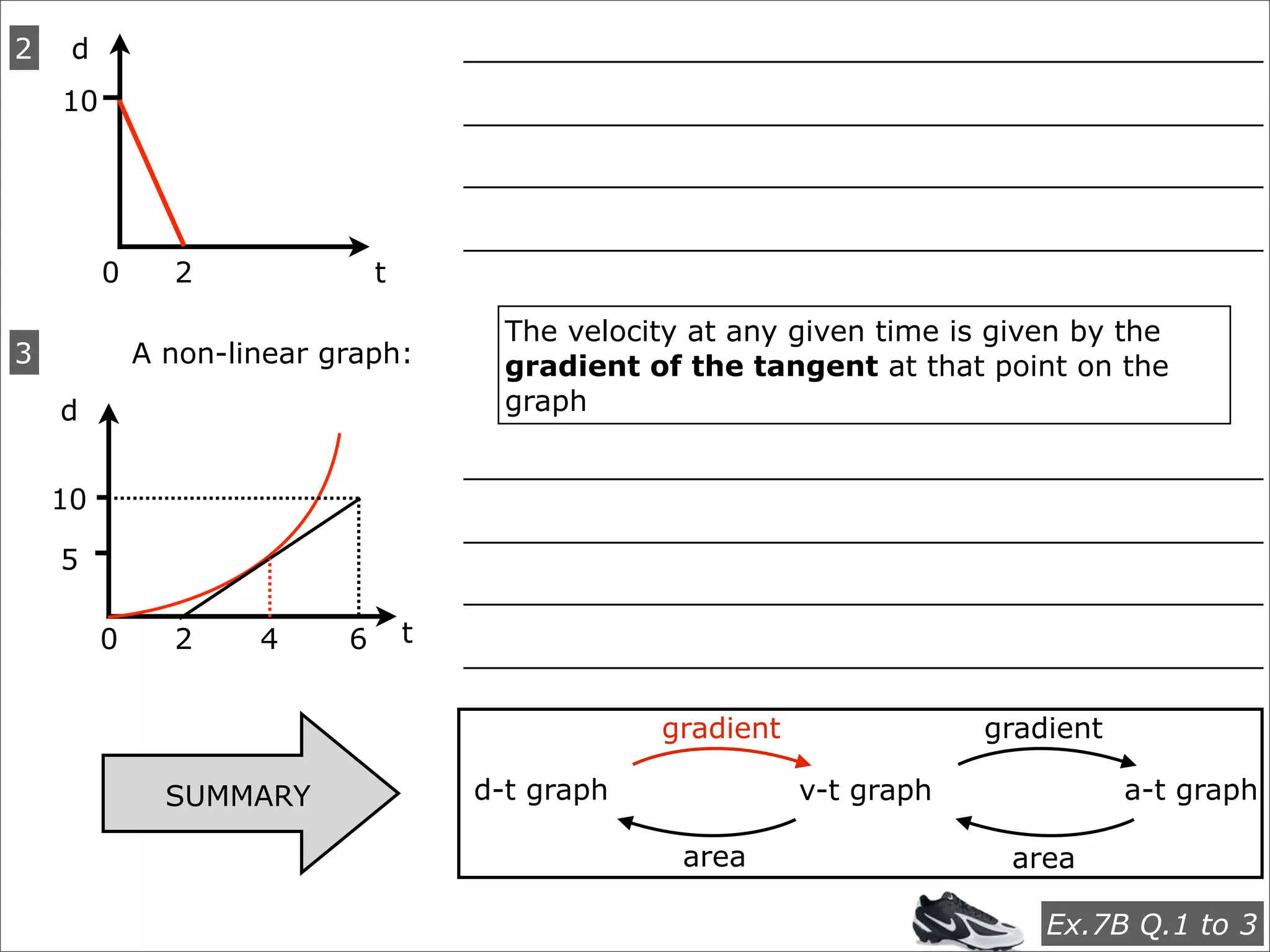
The document discusses concepts related to accelerated motion including: - Constant acceleration in a straight line and projectile motion. - Components of relative motion including change in velocity and the velocity vector. - Circular motion involving constant speed with a single centripetal force. - Key equations for uniformly accelerated motion are listed to solve related problems.

1. ACCELERATED MOTION
constant acceleration in a straight line; free fall under gravity, projectile motion; Relative motion, change in velocity, velocity vector
components, circular motion (constant speed with one force only providing centripetal force).
1. Describe the difference between distance and displacement
2. Describe the difference between speed and velocity and calculation speed and
velocity from distance and displacement
3. Calculate the acceleration of moving objects when information relating to speed
and time are known.
4. Construct a velocity - time graph from ticker tape
5. Determine distance and acceleration from a velocity - time graph
6. Find the velocity from a distance - time graph and make general interpretations of
the nature of the velocity from distance - time sketches
7. Remember these equations for uniformly accelerated motion, and use
them to solve problems:
d = (vf + vi) t
vf = vi + at , 2
vf vi2 + 2ad d = vi t +
1
at 2
= 2
2

2. DISTANCE AND DISPLACEMENT
Distance is the total path length from the starting point to the end point of a
journey.
Displacement means the “shift in an object’s position”. When we state the
displacement of an object we are describing its distance from the starting point and
the direction of the shift from the starting point. We describe the object’s position.
(In other words “displacement is distance with direction”)
Distance, d is called a scalar quantity
A scalar is a physical quantity which has size only
(Examples of scalar quantities: Mass, Temperature, Volume)
Displacement, d is a vector quantity.
~
A vector is a physical quantity which has both size and direction
(Examples of vector quantities: Velocity, Acceleration and Force)
“~” shows a vector quantity
Example 1
An athlete runs 400 m around an athletics track. He starts and finishes in the same
place.
The distance travelled is 400 m (this is the total path length). The displacement is
0m (because the runner has not shifted from the starting point)

3. Example 2
A boat travels from the Whakatane ramp and out to White Island which is 15 km
away. White Island is 5o East of North from Whakatane.
The distance travelled = 15 km
The displacement from the start = 15 km @ 5o E of N
We use arrows to show displacement:
White Island
A bearing is an angle measured
clockwise from North
5o 15 km
5o written as bearing would be 005o
Whakatane
Example 3
Consider an object which has moved from point A to point B by first travelling 3 km
North and then travelling 4 km East:
For the journey: distance travelled, d = 3 + 4
= 7 km
displacement from the start, d = 5 km @ 530 E of N
~

4. Example 2
A boat travels from the Whakatane ramp and out to White Island which is 15 km
away. White Island is 5o East of North from Whakatane.
The distance travelled = 15 km
The displacement from the start = 15 km @ 5o E of N
We use arrows to show displacement:
White Island
A bearing is an angle measured
clockwise from North
5o 15 km
5o written as bearing would be 005o
Whakatane
Example 3
Consider an object which has moved from point A to point B by first travelling 3 km
North and then travelling 4 km East:
For the journey: distance travelled, d = 3 + 4
= 7 km
displacement from the start, d = 5 km @ 530 E of N
A ~

5. Example 2
A boat travels from the Whakatane ramp and out to White Island which is 15 km
away. White Island is 5o East of North from Whakatane.
The distance travelled = 15 km
The displacement from the start = 15 km @ 5o E of N
We use arrows to show displacement:
White Island
A bearing is an angle measured
clockwise from North
5o 15 km
5o written as bearing would be 005o
Whakatane
Example 3
Consider an object which has moved from point A to point B by first travelling 3 km
North and then travelling 4 km East:
For the journey: distance travelled, d = 3 + 4
3 km = 7 km
displacement from the start, d = 5 km @ 530 E of N
A ~

6. Example 2
A boat travels from the Whakatane ramp and out to White Island which is 15 km
away. White Island is 5o East of North from Whakatane.
The distance travelled = 15 km
The displacement from the start = 15 km @ 5o E of N
We use arrows to show displacement:
White Island
A bearing is an angle measured
clockwise from North
5o 15 km
5o written as bearing would be 005o
Whakatane
Example 3
Consider an object which has moved from point A to point B by first travelling 3 km
North and then travelling 4 km East:
4 km
For the journey: distance travelled, d = 3 + 4
3 km = 7 km
displacement from the start, d = 5 km @ 530 E of N
A ~

7. Example 2
A boat travels from the Whakatane ramp and out to White Island which is 15 km
away. White Island is 5o East of North from Whakatane.
The distance travelled = 15 km
The displacement from the start = 15 km @ 5o E of N
We use arrows to show displacement:
White Island
A bearing is an angle measured
clockwise from North
5o 15 km
5o written as bearing would be 005o
Whakatane
Example 3
Consider an object which has moved from point A to point B by first travelling 3 km
North and then travelling 4 km East:
4 km B
For the journey: distance travelled, d = 3 + 4
3 km = 7 km
displacement from the start, d = 5 km @ 530 E of N
A ~

8. Example 2
A boat travels from the Whakatane ramp and out to White Island which is 15 km
away. White Island is 5o East of North from Whakatane.
The distance travelled = 15 km
The displacement from the start = 15 km @ 5o E of N
We use arrows to show displacement:
White Island
A bearing is an angle measured
clockwise from North
5o 15 km
5o written as bearing would be 005o
Whakatane
Example 3
Consider an object which has moved from point A to point B by first travelling 3 km
North and then travelling 4 km East:
4 km B
For the journey: distance travelled, d = 3 + 4
3 km = 7 km
53o 5 km
displacement from the start, d = 5 km @ 530 E of N
A ~

9. Example 4
A toy train travels 0.4 m North, 0.6 m East and 1.0 m South. The time for this journey
is 5 s.
(a) What is the total distance covered by the train?
_________________________________________________________________
(b) Use the grid below to determine the displacement of the train over this journey?
N
W E
on grid = 0.1 m
displacement = _________________________

10. SPEED AND VELOCITY
Speed is a scalar quantity. It is how fast the object is travelling. It is the rate of change of
distance.
Velocity is a vector quantity (it refers to the object’s speed and the direction in which the object
moves)
Speed = change in distance = ∆d
Equation 1
change in time ∆t
Velocity = change in displacement = ∆d
~ Equation 2
change in time ∆t
∆ = “change in”
v = speed
v = velocity ( both have the same unit: ms-1)
~
The equations always calculate the average speed or average velocity
Velocity calculations - Process
1. Calculate the size of the change in displacement (using a diagram if you have to)
2. Apply equation 2
3. State your answer, including units and direction
Note
Speed or velocity can be instantaneous. This is the speed or velocity at an instant in
time.

11. Example 1
A girl walks in a straight line from the hair salon to her home. Her position at 30 s is 20 m North
of the salon and her position at 60 s is 50 m North of the salon. Calculate the girl’s speed and
her velocity during the section of the journey described.
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
Example 2
A toy train travels 0.3 m North, 0.7 m East and 0.9 m South. The time for this journey is 5 s.
(a) Calculate the speed of the train for the entire journey
_________________________________________________________________
(b) Calculate the velocity of the train for the entire journey
_________________________
N _________________________
_________________________
W E
_________________________
velocity = ________________
on grid = 0.1 m

12. ACCELERATION
Acceleration is how fast the velocity changes. It is a vector quantity because
velocity is a vector quantity.
Acceleration = change in velocity = ∆v
~
change in time ∆t
Change in velocity = final velocity - initial velocity
∆v = vf - vi
For now we will consider 2 situations:
1. An object travels in the forward direction only, in which case the velocities can
both be considered to be positive
2. An object can travel forwards or backwards along a straight line, in which case
the forward direction can be considered to be positive and the backward direction
can be considered to be negative.
Note
If the final velocity is smaller than the initial velocity then the object has slowed
down. The value of acceleration will be negative.
A negative value of acceleration is called deceleration.

13. Acceleration calculations - Process
1. Show the positive and negative direction as part of your working.
2. Calculate the change in velocity, using positive and negative values in your
calculation.
3. Determine the change in time
EXAMPLES
4. Use the formula to calculate the acceleration
(a) A motorcyclist speeds up from 2 ms-1 to 22 ms-1 in a time of 10 s. Calculate his
acceleration.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
(b) The same motorcyclist travels at a constant speed of 22 ms-1 for a few seconds
and then slows down for a set of traffic lights which have turned red. He takes 11
s to stop. Calculate his acceleration.
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
_________________________________________________________________
Ex.7A Q.1 to 8

14. INTERPRETING VELOCITY - TIME GRAPHS
Consider a ball rolling on a flat surface (in the absence of friction). It has a constant
speed of 4 ms-1. Calculate the distance that the ball has travelled in that 5 s.
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
The graph of the ball’s motion for the first 5 s is shown in the speed-time graph below:
v (ms-1)
5 A calculation of the area under the graph
4 gives a distance covered of 20 m which
3 is the same as value achieved from
2 A rearranging the equation:
v = d
1
t
0 1 2 3 4 5 t (s)
When speed is constant the distance travelled can be calculated using:
d = v.t This works in this situation because there is a single value for speed which
is the same for the entire time, t that the object is moving.

15. If the ball were to roll down a sloping surface (in the absence of friction) then its
speed would increase. The speed would increase at a constant rate. In other words
the acceleration would be constant. We would expect this because gravity is causing
this increase in speed and because this force is constant then the acceleration would
be constant. (Force causes acceleration according to the equation F = ma)
The graph of the ball’s motion for the first 5 s would be a straight line sloping upwards
and might look like this:
v (ms-1) A calculation of the area under the graph
5 gives the distance covered:
4
3 d = Area = 1 x 5 x 52 = 12.5 m
2
2
A
1
The area under a velocity - time graph
0 1 2 3 4 5 t (s) gives the distance travelled
When speed is changing the distance travelled can not be calculated using:
d = v.t This is because v is changing. There is no single value of v that can be
used.

16. Again considering the ball rolling down the slope, we know that the acceleration is
constant. Acceleration can be calculated using the following equation:
Acceleration = change in velocity = ∆v
~
change in time ∆t
The graph again will look like this:
v (ms-1)
vf = 5
5
4
3 ∆ v = vf - vi
2 =5-0
A
1 vi = 0 =5
The Rise
0 1 2 3 4 5 t (s)
∆ t = tf - ti = 5 - 0 = 5
The Run
a = ∆v = 5 = 1 ms-2 in other words a = rise = gradient of the graph
∆t 5 run

17. Examples
1. For the above graph, calculate the distance travelled:
(i) between 0s and 4s
________________________________________________________________
(ii) between 5s and 10s
________________________________________________________________
2. Calculate the acceleration of the object
(i) in the first 4s
________________________________________________________________
(ii) between 4s and 7s
________________________________________________________________
(iii) between 7s and 10s
________________________________________________________________

18. 3. The velocity - time graph below shows the motion of a cyclist along a straight road.
Complete the table (to the right of the graph) to show the acceleration of the cyclist in each
time interval:
Time interval (s) Acceleration (ms-2)
0 to 10
10 to 25
25 to 35
35 to 40
40 to 45
Calculate the distance travelled by the cyclist during the 45 s ride.
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________
Calculate the displacement of the cyclist at 45 s.
____________________________________________________________________________
____________________________________________________________________________
____________________________________________________________________________

19. INTERPRETING DISPLACEMENT - TIME GRAPHS
The gradient of a displacement - time graph gives
the velocity of the object.
This principle can be used to label the following Steady speed Stopped
graphs from the list of labels given (right) Acceleration Deceleration
d d d d
Example t t t t
Calculate the velocity from the following distance - time graphs.
1 d Gradient = Rise = 10 = 2 ms-1
10 Run 5
So velocity is 2 ms-1
The gradient of a graph is a measure of how
0 t
5 steep the graph is.

20. 2 d ____________________________________________
10 ____________________________________________
____________________________________________
____________________________________________
0 2 t
The velocity at any given time is given by the
3 A non-linear graph: gradient of the tangent at that point on the
d graph
____________________________________________
10
____________________________________________
5
____________________________________________
0 2 4 6 t
____________________________________________
gradient gradient
SUMMARY d-t graph v-t graph a-t graph
area area
Ex.7B Q.1 to 3

21. KINEMATIC EQUATIONS
These equations apply to situations in which the acceleration is
constant:
d = displacement (i.e. distance from the start in the
positive or negative direction)
a = acceleration (positive or negative) Mostly vector quantities
t = time
vf = final velocity (positive or negative)
vi = initial velocity (positive or negative)

22. Process
1. Read the question carefully and underline the relevant information.
2. List the 5 symbols on your page in specific order and write in the known quantities in SI units:
d=
vi =
vf =
a=
t=
3. Use a “?” to indicate the quantity that you want to calculate and if a quantity is not given then
leave it blank.
4. Only three quantities are required out of the five to perform a calculation.
5. Select the equation that you will use based on which of the five quantities is not given.
6. Rearrange the equation to make the required quantity the subject.
7. Substitute the numerical values into the equation and evaluate.
Introduction to rearranging equations
Examples
1. A stone is released from a height of 20 m above the ground. Neglecting air
resistance and using the acceleration due to gravity as 9.81 ms-2, find the velocity
with which the stone will hit the ground .
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________
__________________________________________________________________

23. 2. Calculate the uniform acceleration of a sports car which:
(a) starts from rest and reaches a speed of 15 ms-1 in 10 s.
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
(b) changes its speed from 20 ms-1 to 32 ms-1 in 4.0 s.
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
(c) starts from rest and travels a distance of 98 m in 7.0 s.
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
(d) slows down from a speed of 66 ms-1 and comes to rest in 12 s.
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________

24. 3. A ball rolls from rest down an incline with a uniform acceleration of 4.0 ms-2.
(a) What is its speed after 8.0 s?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
(b) How long will it take to reach a speed of 36 ms-1?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
(c) How long does it take to travel a distance of 200 m, and what is its speed after
that time?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
(d) How far does it travel during the third second of its motion?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________

25. 4. A model train moving at 20 cms-1 increases its speed uniformly to 60 cms-1 in 5.0 s
(a) What was the trains acceleration?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
(b) What distance was travelled in that time?
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
5. A car accelerating uniformly, reaches a speed of 30 ms-1 from rest in 3.0 min.
Calculate its acceleration and the distance travelled in this time. Later it comes to
rest in 20 s when the brakes are applied. Find the deceleration and the distance
covered while it is slowing down.
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________________________________
___________________________________________
Ex.7C Q.1 to 5

26. 12 PHYSICS KINEMATICS MINI ASSIGNMENT Name ___________________
1. A skateboarder starts a rail slide at 8.0 ms-1 and accelerates at 6.0 ms-2 to reach a
speed of 10 ms-1 at the bottom of the rail. How long is the rail?
2. A car slows from 25 ms-1 to 15 ms-1 over a distance of 400 m.
(a) What is the deceleration of the car?
(b) Calculate the time taken for the car to slow.
3. A car is travelling at 12 ms-1. At t = 0 it accelerates at 1.5 ms-2 to a speed of
18 ms-1.
(a) Calculate the time taken for the car to reach the final speed of 18 ms-1.
(b) Calculate the distance travelled in this time.
(c) What is the car’s speed once it has travelled 100 m?
4. A driver is travelling steadily at 12 ms-1 when he spots a dog 48 m ahead. After a
reaction time of 0.75 s, he applies the brakes and stops. The brakes produce a
steady deceleration of 2.0 ms-2.
(a) Calculate how far he travels during his reaction time (with no braking).
(b) Calculate how far he travels while he is braking.
(c) What happens to the dog?

27. 5. A plane drops a Red Cross package from a height of 1200 m. If the package had no
parachute (and by this you can assume negligible air friction):
(a) How fast will the package be travelling just before it hits the ground?
(b) How many seconds will the package take to fall?
6. A 1 kg object is dropped from a tower 120 m high.
(a) Calculate the time it will take for the object to fall to the ground.
(b) Calculate the objects final speed on reaching the ground.
(c) How long does it take to reach a speed of 35 ms-1 ?
7. A shell is fired straight up with an initial speed of 96 ms-1.
(a) Calculate the time it will take for the object to fall to the ground.
(b) When will the shell have an upwards speed of 48 ms-1 ?
(c) Calculate the time for the shell to reach its maximum height.
(d) Calculate the maximum height reached by the shell.
(e) What is the shells acceleration at the top of its motion?