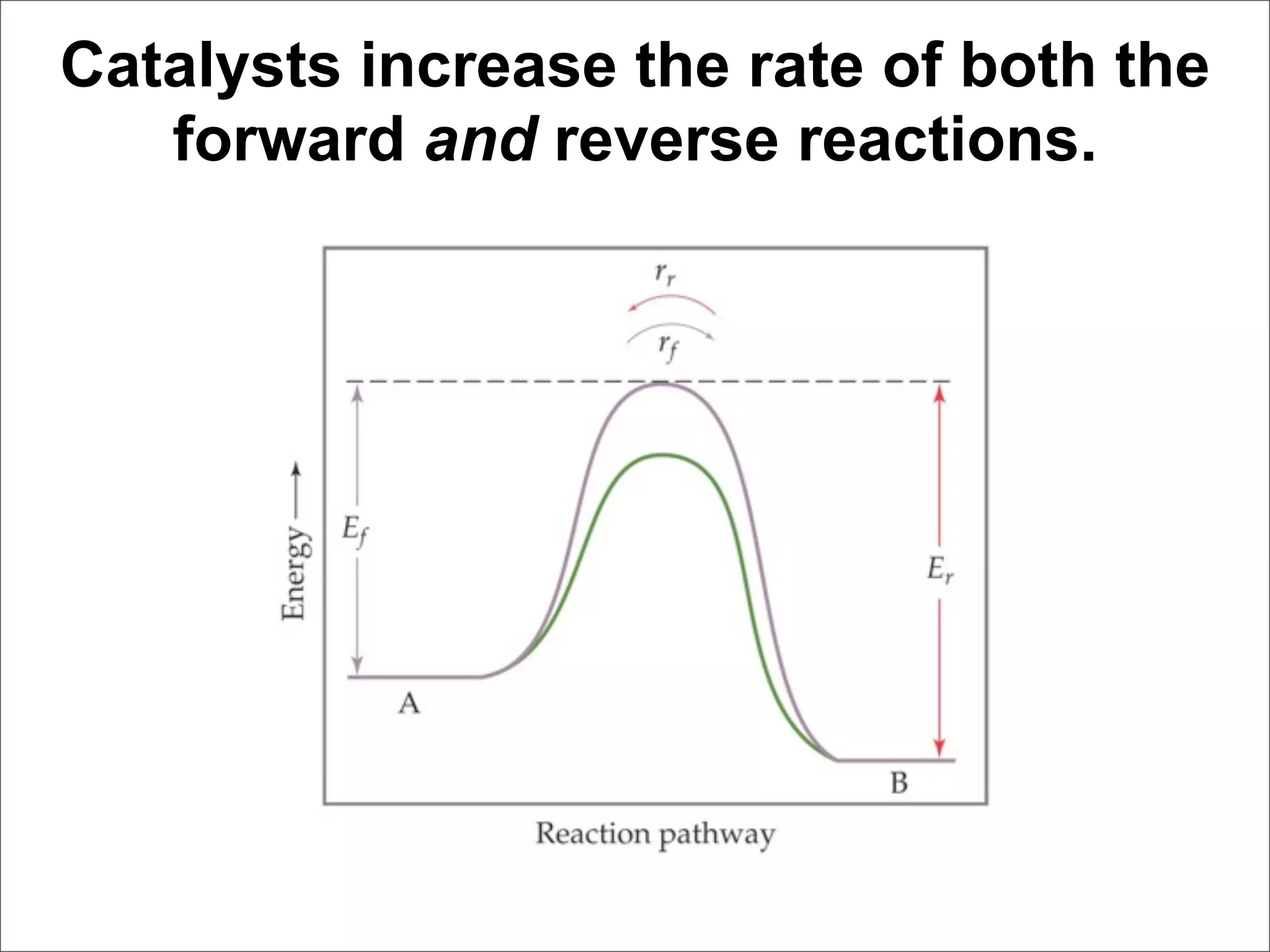
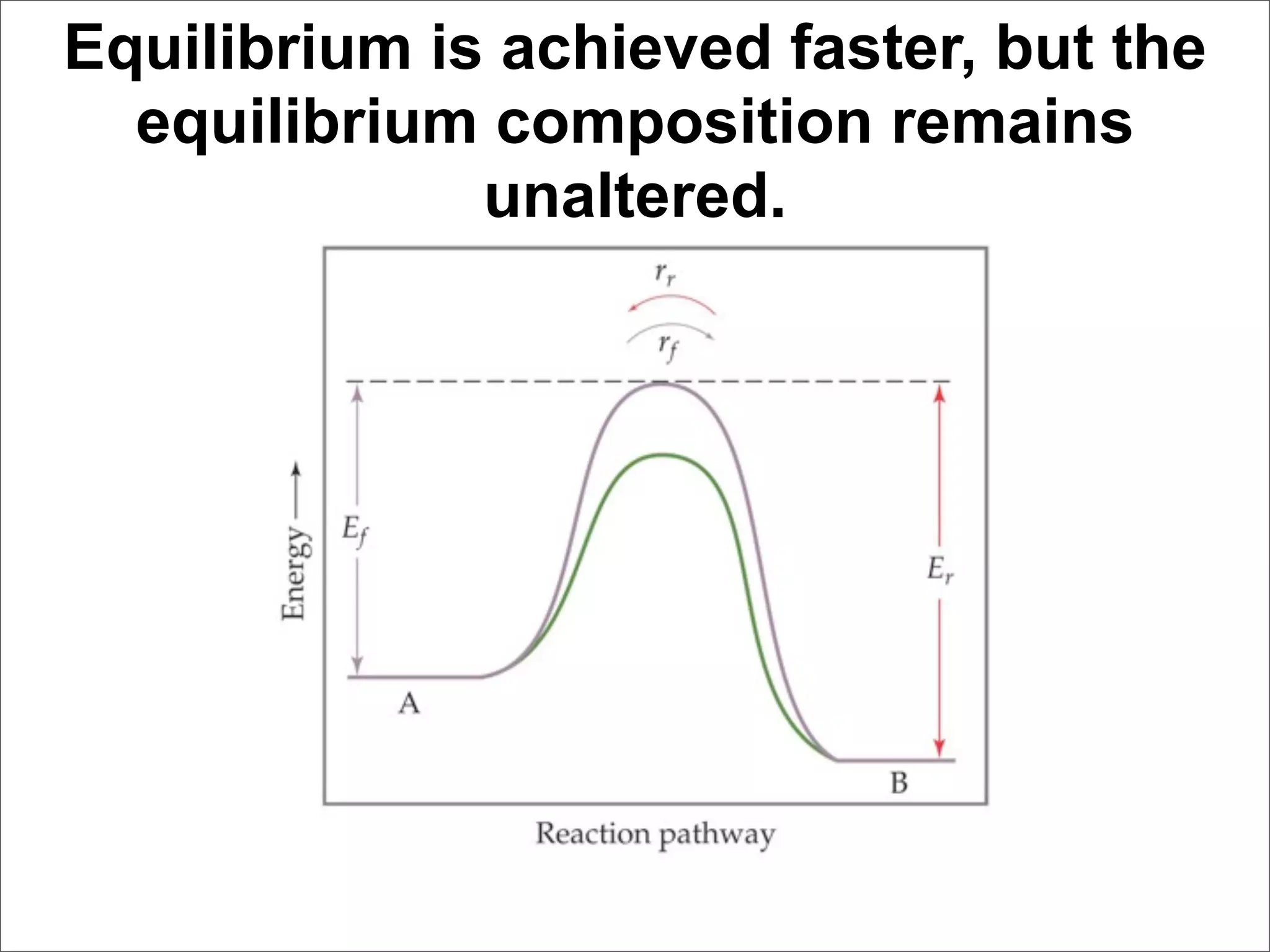
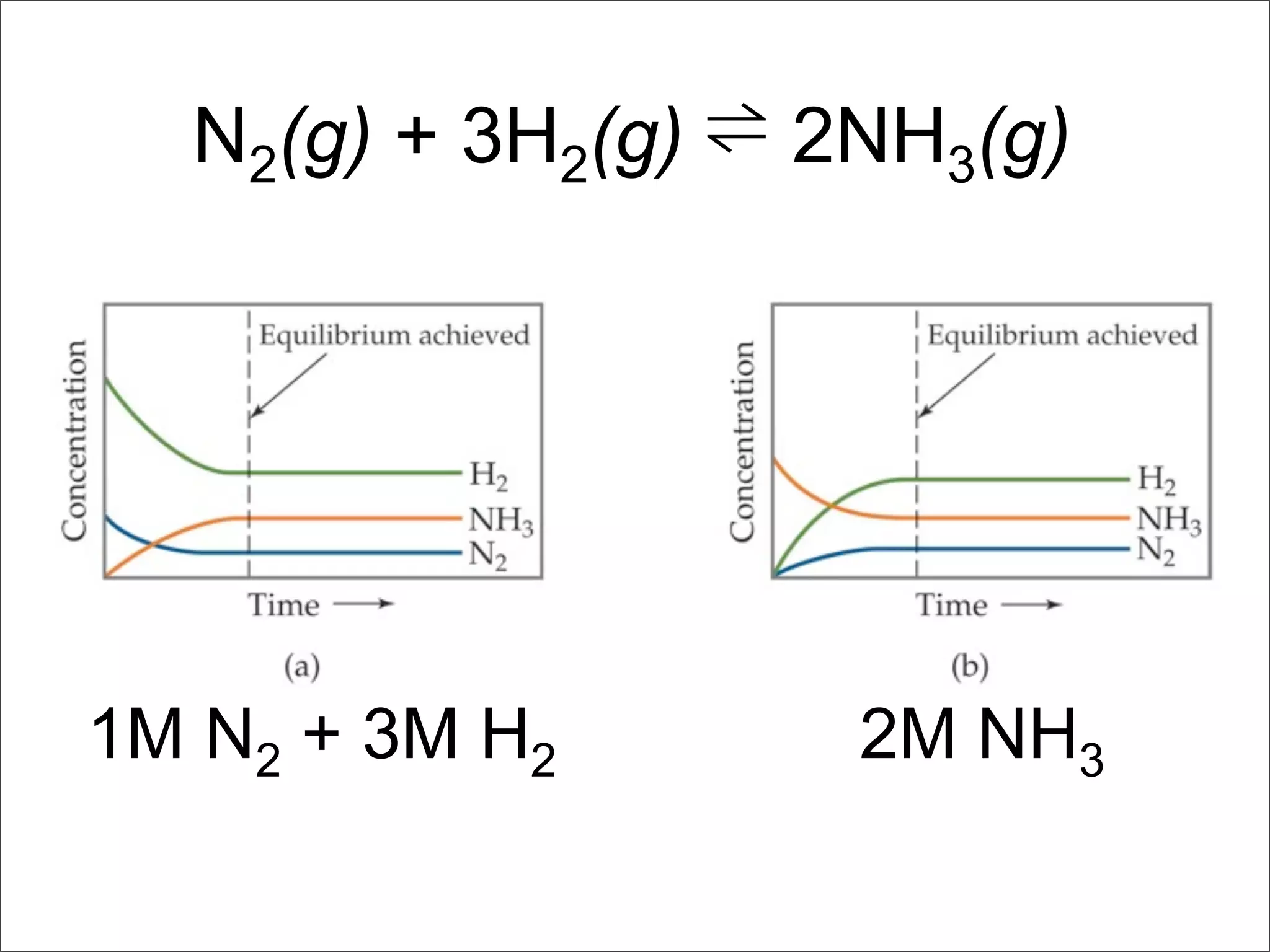
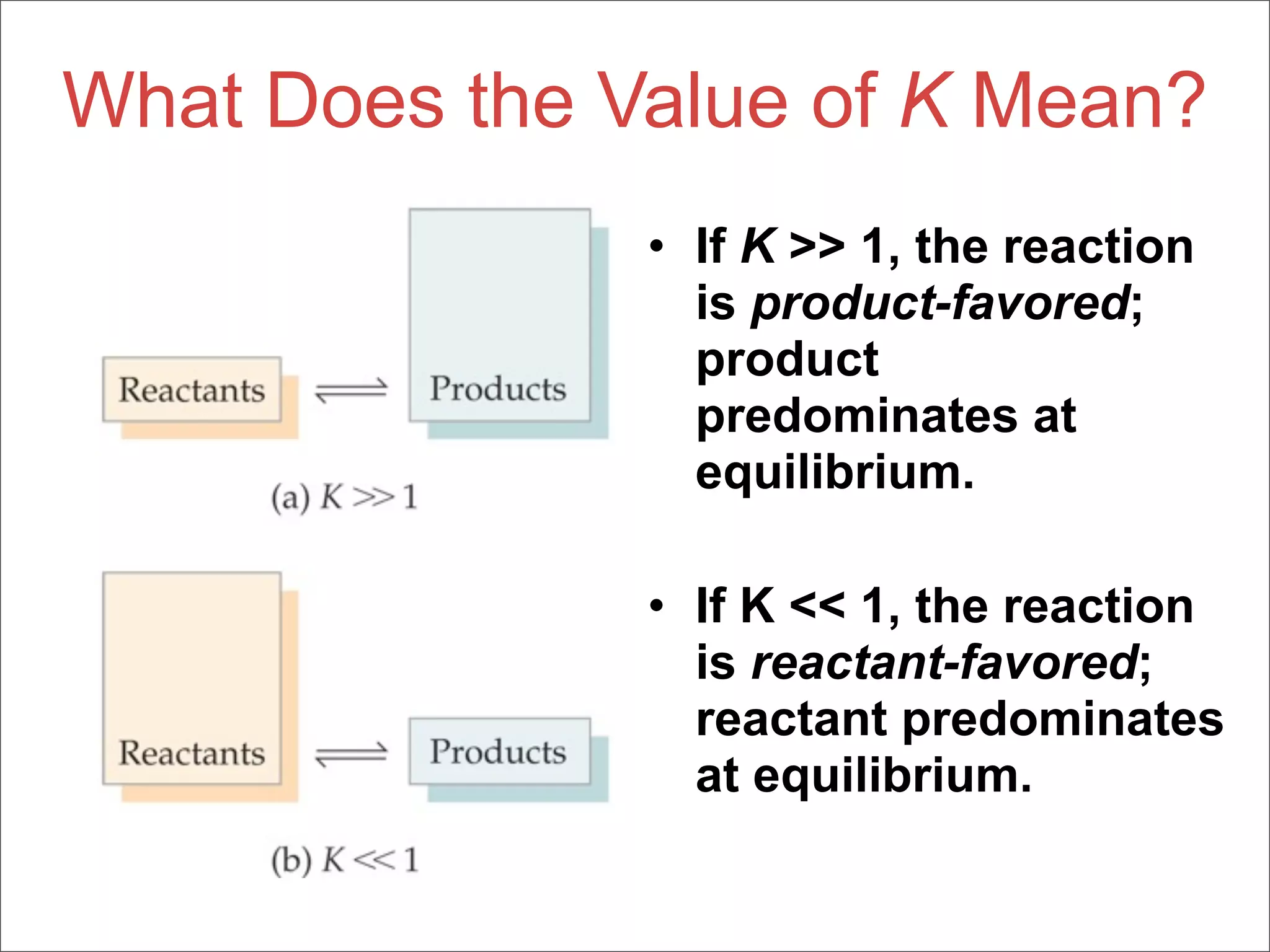
1. The document discusses chemical equilibrium, including the concepts of equilibrium, depicting equilibrium reactions with equations, the equilibrium constant K, and how the value of K relates to whether a reaction favors reactants or products.
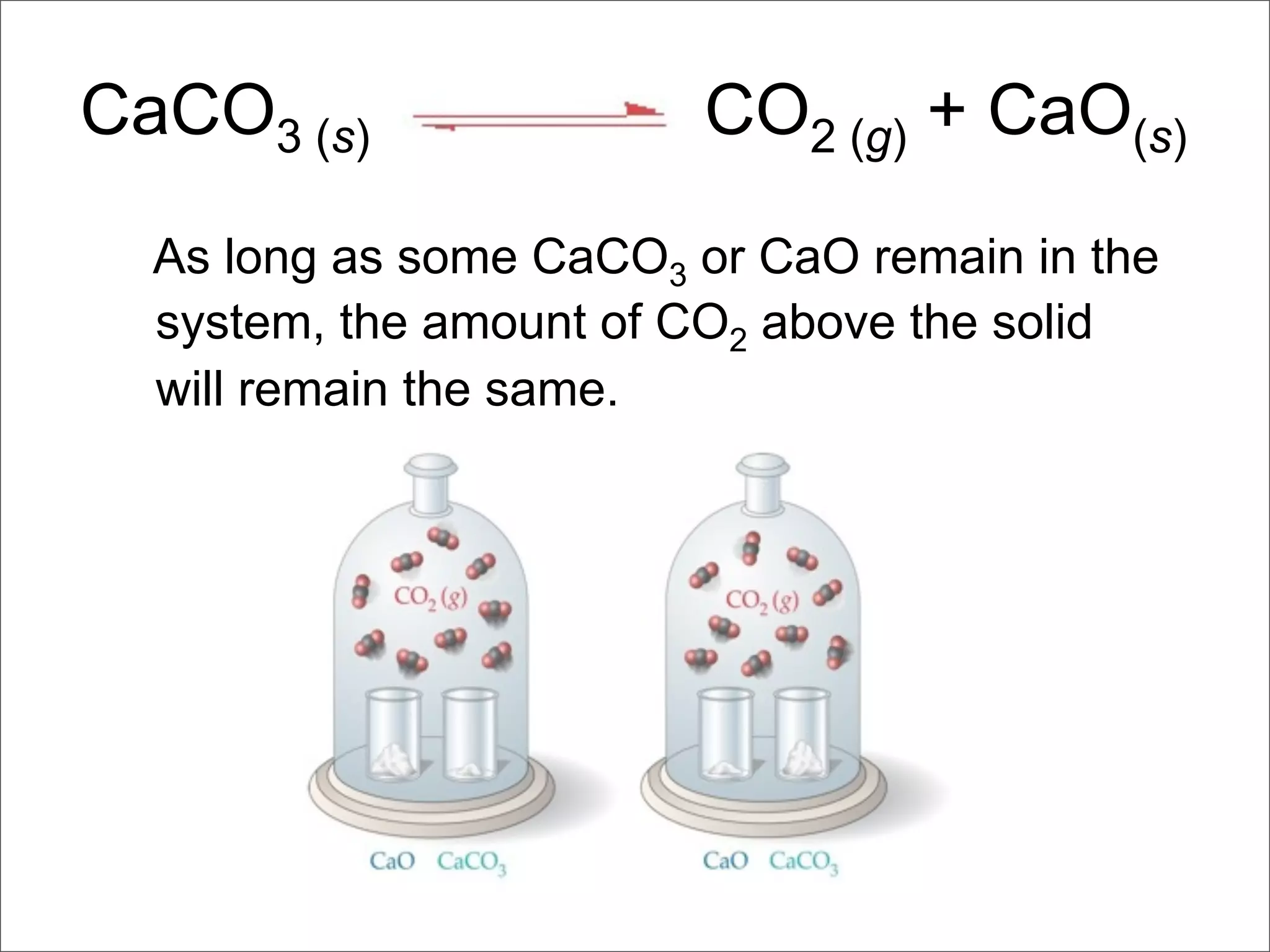
2. It also covers heterogeneous equilibria involving solids or liquids, how the concentrations of solids and liquids do not appear in equilibrium expressions, and examples of heterogeneous equilibrium reactions like the decomposition of calcium carbonate.
3. The key aspects covered are the definition of chemical equilibrium as when forward and reverse reactions proceed at the same rate, the use of concentration ratios and partial pressures to define equilibrium constants Kc and Kp, and how heterogeneous reactions involve gases in equilibrium with solids or liquids.


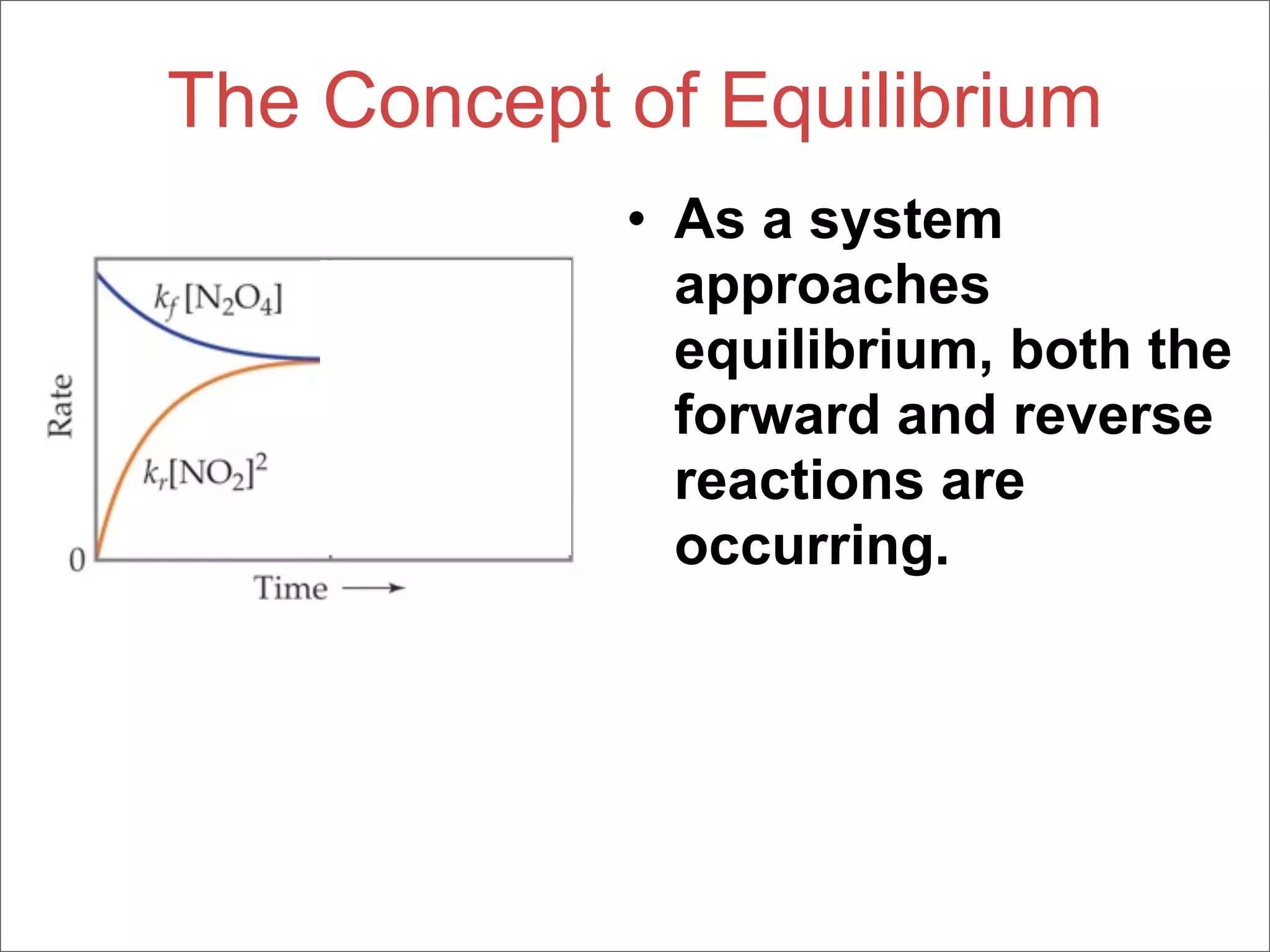




![The Equilibrium Constant
• Forward reaction:
N2O4 (g) → 2 NO2 (g)
✤Rate law: Rate = kf [N2O4]](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-9-2048.jpg)
![The Equilibrium Constant
• Forward reaction:
N2O4 (g) → 2 NO2 (g)
✤Rate law: Rate = kf [N2O4]
• Reverse reaction:
2 NO2 (g) → N2O4 (g)
✤Rate law: Rate = kr [NO2]2](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-10-2048.jpg)
![The Equilibrium Constant
• Therefore, at equilibrium
Ratef = Rater
kf [N2O4] = kr [NO2]2](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-11-2048.jpg)
![The Equilibrium Constant
• Therefore, at equilibrium
Ratef = Rater
kf [N2O4] = kr [NO2]2
• Rewriting this, it becomes
kf [NO2]2
=
kr [N2O4]](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-12-2048.jpg)
![The Equilibrium Constant
The ratio of the rate constants is a
constant at that temperature, and the
expression becomes
kf [NO2]2
Keq = =
kr [N2O4]](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-13-2048.jpg)
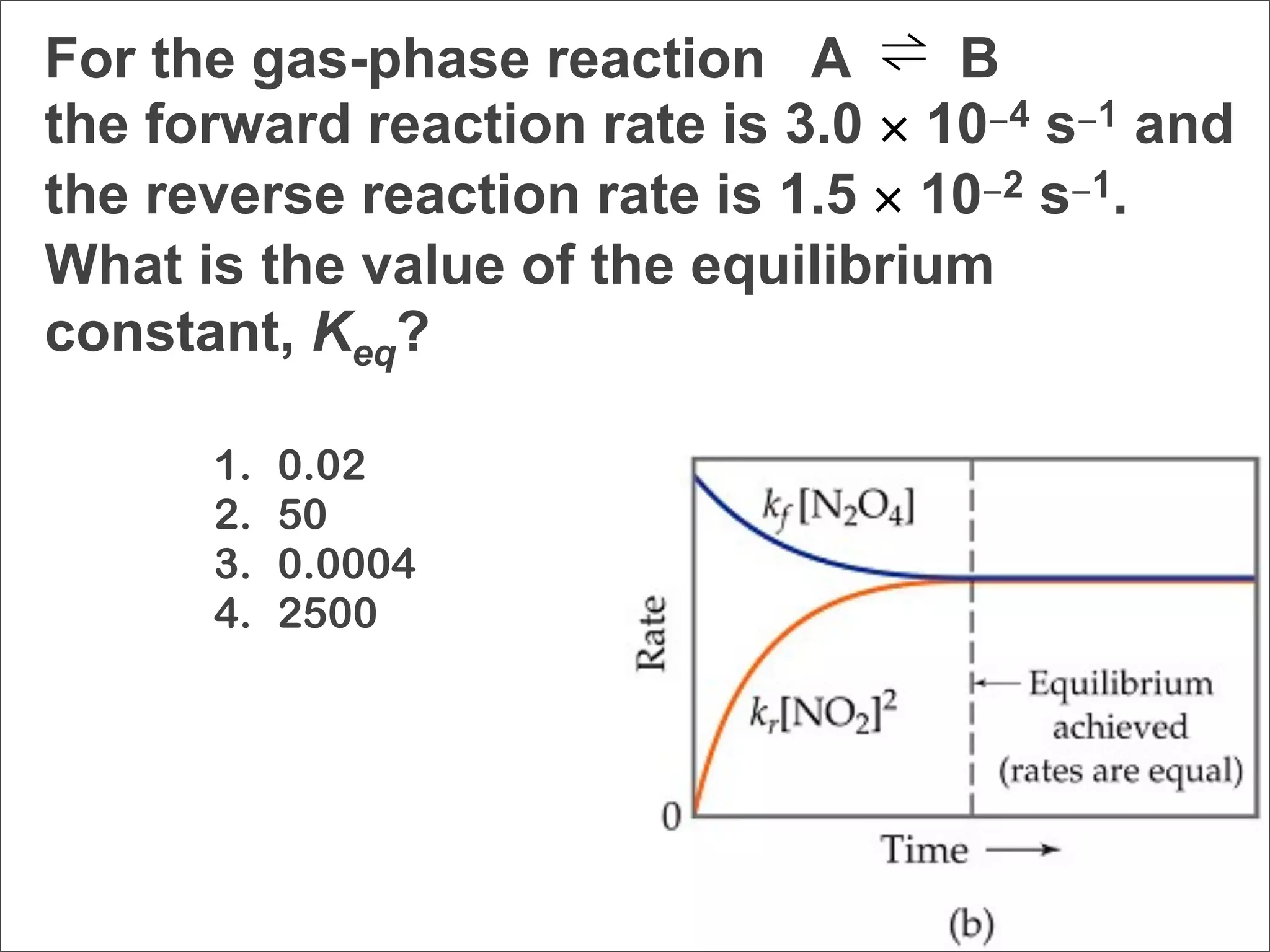

![N2O4 (g) → 2 NO2 (g) Eq 15.1
kf [NO2]2 Eq 15.5
Keq = k = [N O ]
r 2 4
1. moles of reactant always equals moles of
product.
2. mass of reactant always equals mass of product.
3. the rates of opposing reactions are equal.
4. cannot be determined without temperature
information.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-16-2048.jpg)
![N2O4 (g) → 2 NO2 (g) Eq 15.1
kf [NO2]2 Eq 15.5
Keq = k = [N O ]
r 2 4
1. moles of reactant always equals moles of
product.
2. mass of reactant always equals mass of product.
3. the rates of opposing reactions are equal.
4. cannot be determined without temperature
information.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-17-2048.jpg)
![N2O4 (g) → 2 NO2 (g) Eq 15.1
kf [NO2]2
Keq = k = [N O ] Eq 15.5
r 2 4
b) the constant will be______ than 1](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-18-2048.jpg)
![N2O4 (g) → 2 NO2 (g) Eq 15.1
kf [NO2]2
Keq = k = [N O ] Eq 15.1
r 2 4
b) the constant will be greater than 1](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-19-2048.jpg)



![The Equilibrium Constant
• To generalize this expression, consider
the reaction
aA + bB cC + dD
• The equilibrium expression for this
reaction would be
[C]c[D]d
Kc =
[A]a[B]b](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-23-2048.jpg)
![The Equilibrium Constant
• To generalize this expression, consider
the reaction
aA + bB cC + dD
• The equilibrium expression for this
reaction would be
[C]c[D]d
Kc =
[A]a[B]b
a.k.a. the LAW of
MASS ACTION](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-24-2048.jpg)













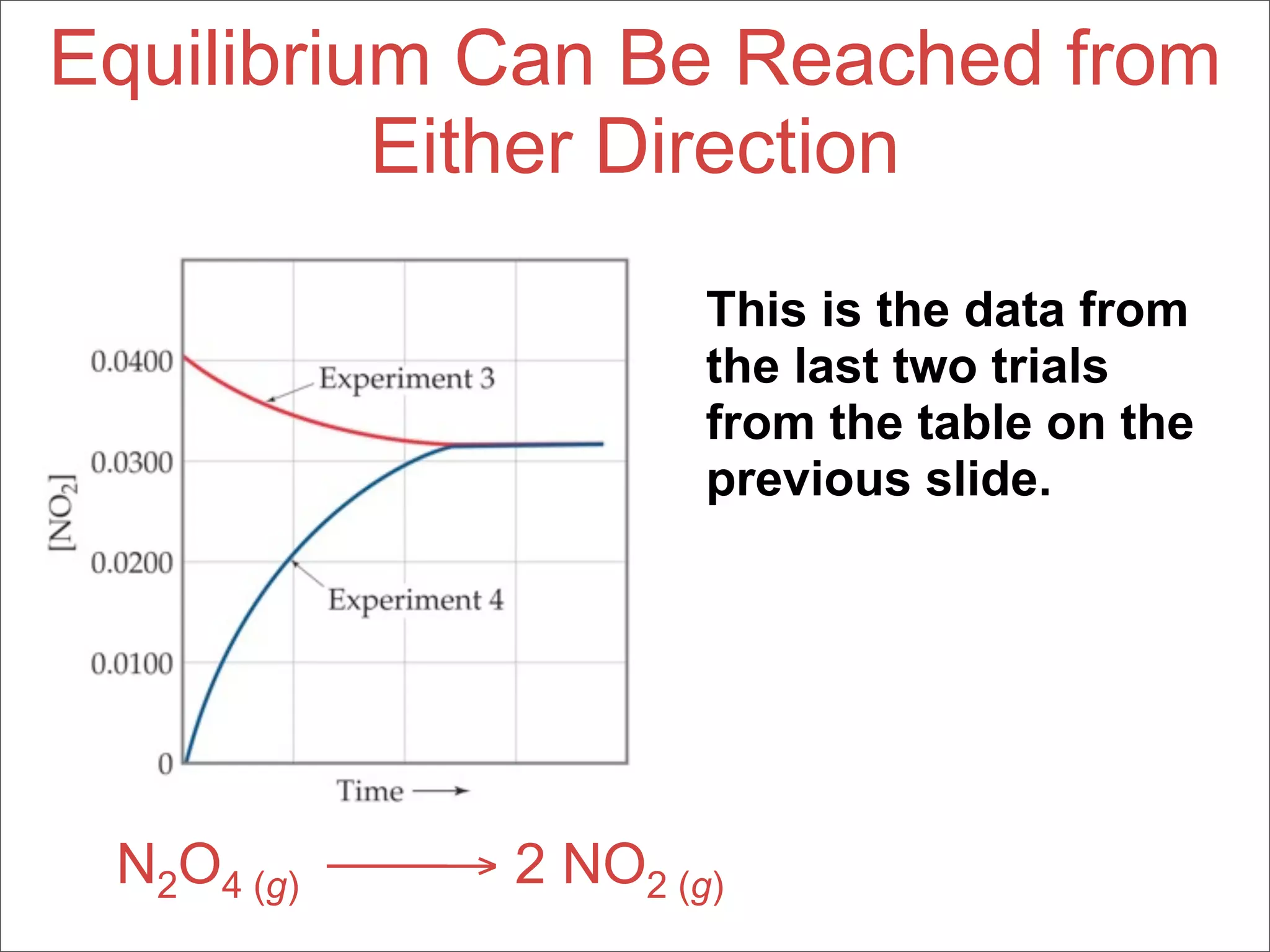
![Equilibrium Can Be Reached from
Either Direction
N2O4 (g) → 2 NO2 (g)
As you can see, the ratio of [NO2]2 to
[N2O4] remains constant at this
temperature no matter what the initial
concentrations of NO2 and N2O4 are.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-38-2048.jpg)




![Manipulating Equilibrium Constants
The equilibrium constant of a
reaction in the reverse reaction is
the reciprocal of the equilibrium
constant of the forward reaction.
[NO2]2
N2O4 (g) 2 NO2(g) Kc = = 0.212 at 100°C
[N2O4]](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-45-2048.jpg)
![Manipulating Equilibrium Constants
The equilibrium constant of a
reaction in the reverse reaction is
the reciprocal of the equilibrium
constant of the forward reaction.
[NO2]2
N2O4 (g) 2 NO2(g) Kc = = 0.212 at 100°C
[N2O4]
[N2O4] 1
2 NO2 (g) N2O4(g) Kc = =
[NO2]2 0.212
= 4.72 at 100°C](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-46-2048.jpg)
![Manipulating Equilibrium Constants
The equilibrium constant of a reaction that has
been multiplied by a number is the equilibrium
constant raised to a power that is equal to that
number.
[NO2]2
N2O4(g) 2 NO2(g) Kc = = 0.212 at 100°C
[N2O4]](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-47-2048.jpg)
![Manipulating Equilibrium Constants
The equilibrium constant of a reaction that has
been multiplied by a number is the equilibrium
constant raised to a power that is equal to that
number.
[NO2]2
N2O4(g) 2 NO2(g) Kc = = 0.212 at 100°C
[N2O4]
[NO2]4
2 N2O4(g) 4 NO2(g) Kc = = (0.212)2 at 100°C
[N2O4]2](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-48-2048.jpg)











![The Concentrations of Solids and
Liquids Are Essentially Constant
Therefore, the concentrations of solids
and liquids do not appear in the
equilibrium expression
PbCl2 (s) Pb2+ (aq) + 2 Cl−(aq)
Kc = [Pb2+] [Cl−]2](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-60-2048.jpg)









![For the following hypothetical reaction:
2 Y(aq) + 3 Z(aq) A(aq)
Calculate Keq given the following
equilibrium concentrations: [A] = 0.50 M,
[Y] = 0.10 M, [Z] = 1.0 M
[C ]c[D ]d
1. 2.5 K eq =
2. 5.0
[A ]a[ ]b
3. 0.40 B
4. 0.025
5. 50.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-71-2048.jpg)
![Correct Answer:
[0.50]
K eq = 2 3
1. 2.5 [0.10] [ ]
1.0
2. 5.0
3. 0.40
4. 0.025
5. 50.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-72-2048.jpg)

![What Do We Know?
[H2], M [I2], M [HI], M
Initially 1.000 x 10-3 2.000 x 10-3 0
Change
At 1.87 x 10-3
equilibrium](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-74-2048.jpg)
![[HI] Increases by 1.87 x 10-3 M
[H2], M [I2], M [HI], M
Initially 1.000 x 10-3 2.000 x 10-3 0
Change +1.87 x 10-3
At 1.87 x 10-3
equilibrium](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-75-2048.jpg)
![Stoichiometry tells us [H2] and [I2]
decrease by half as much
[H2], M [I2], M [HI], M
Initially 1.000 x 10-3 2.000 x 10-3 0
Change -9.35 x 10-4 -9.35 x 10-4 +1.87 x 10-3
At 1.87 x 10-3
equilibrium](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-76-2048.jpg)
![We can now calculate the equilibrium
concentrations of all three compounds…
[H2], M [I2], M [HI], M
Initially 1.000 x 10-3 2.000 x 10-3 0
Change -9.35 x 10-4 -9.35 x 10-4 +1.87 x 10-3
At 6.5 x 10-5 1.065 x 10-3 1.87 x 10-3
equilibrium](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-77-2048.jpg)
![…and, therefore, the equilibrium
constant
[HI]2
Kc =
[H2] [I2]
(1.87 x 10-3)2
=
(6.5 x 10-5)(1.065 x 10-3)
= 51](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-78-2048.jpg)




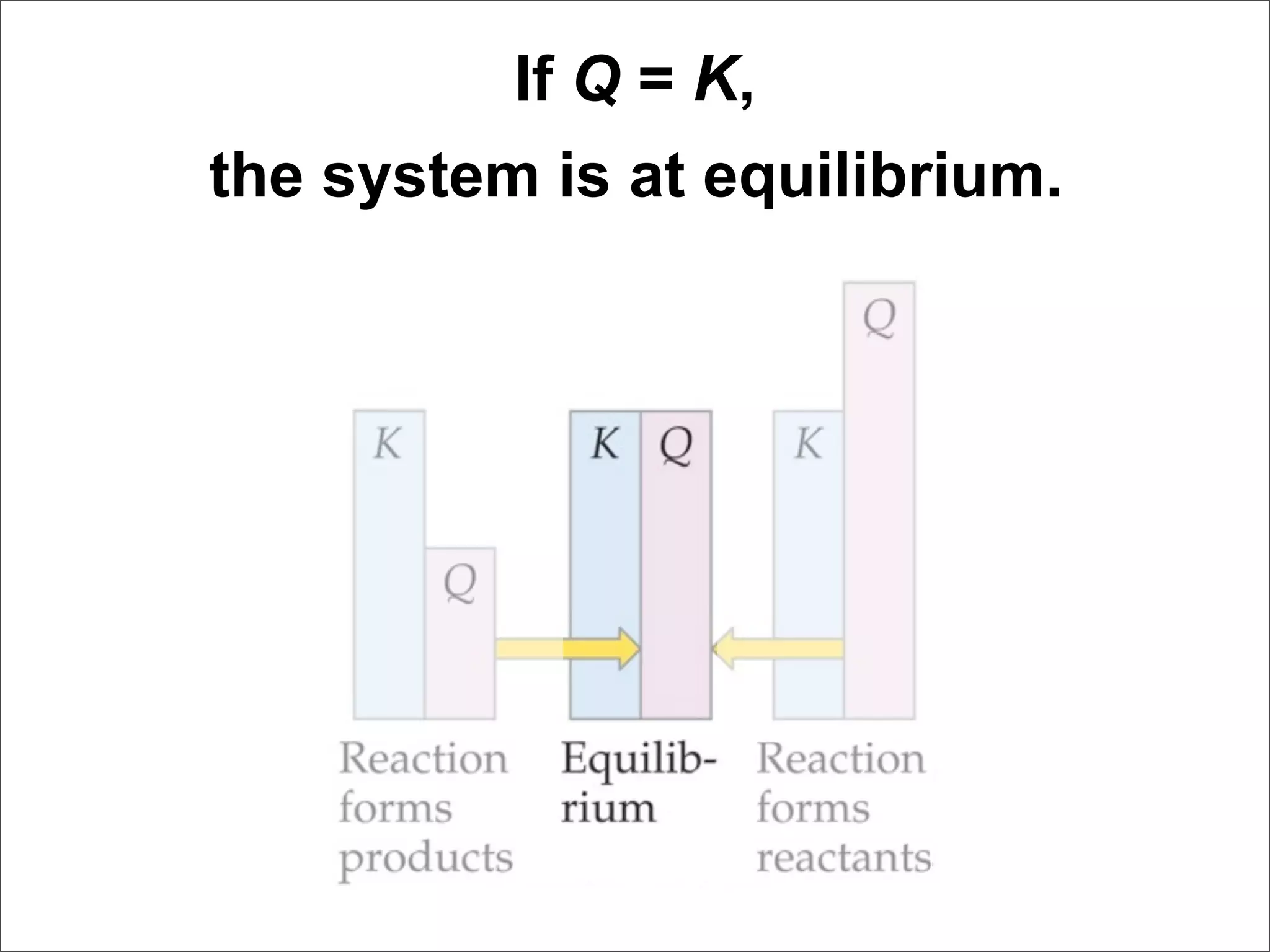
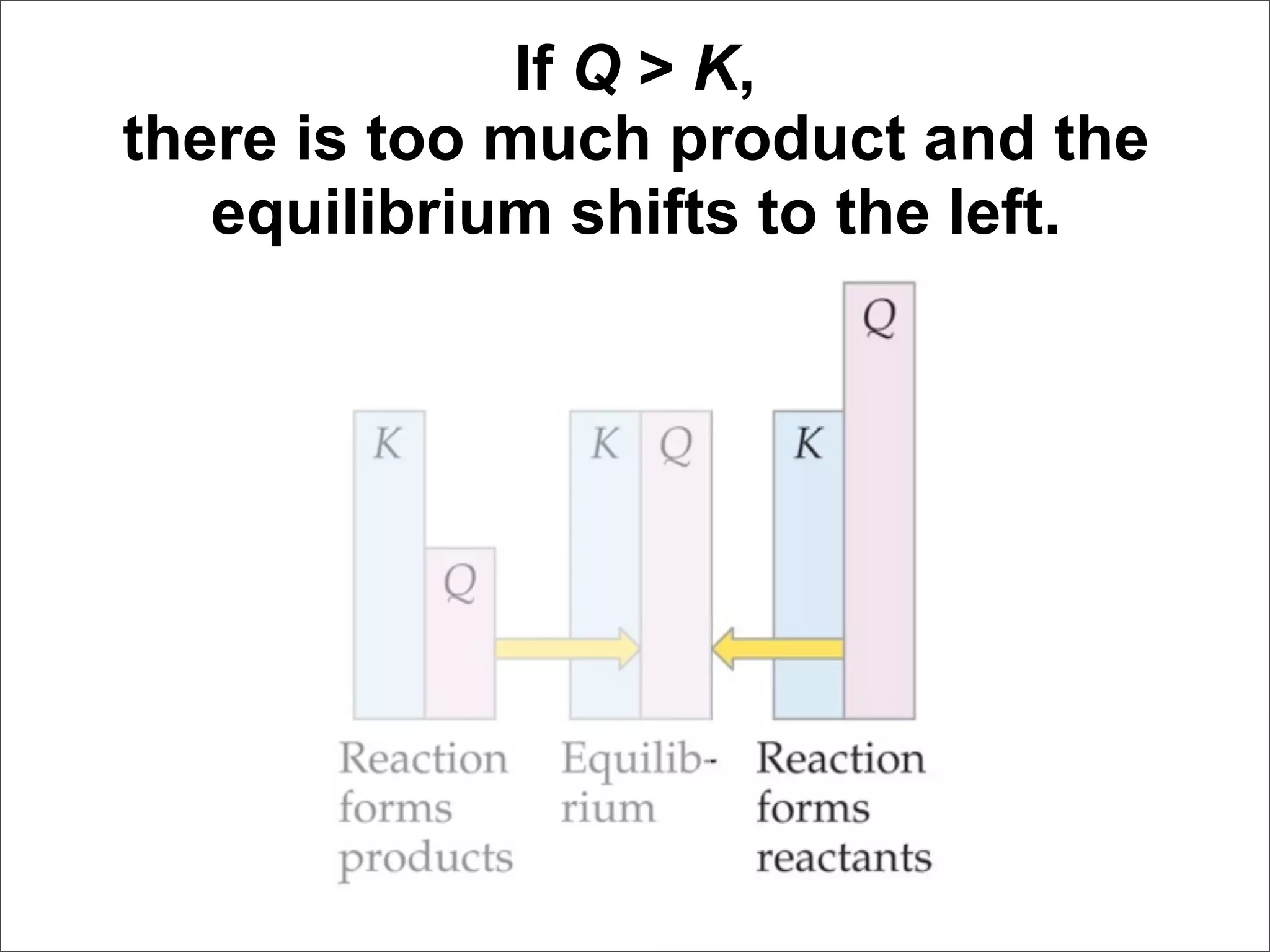
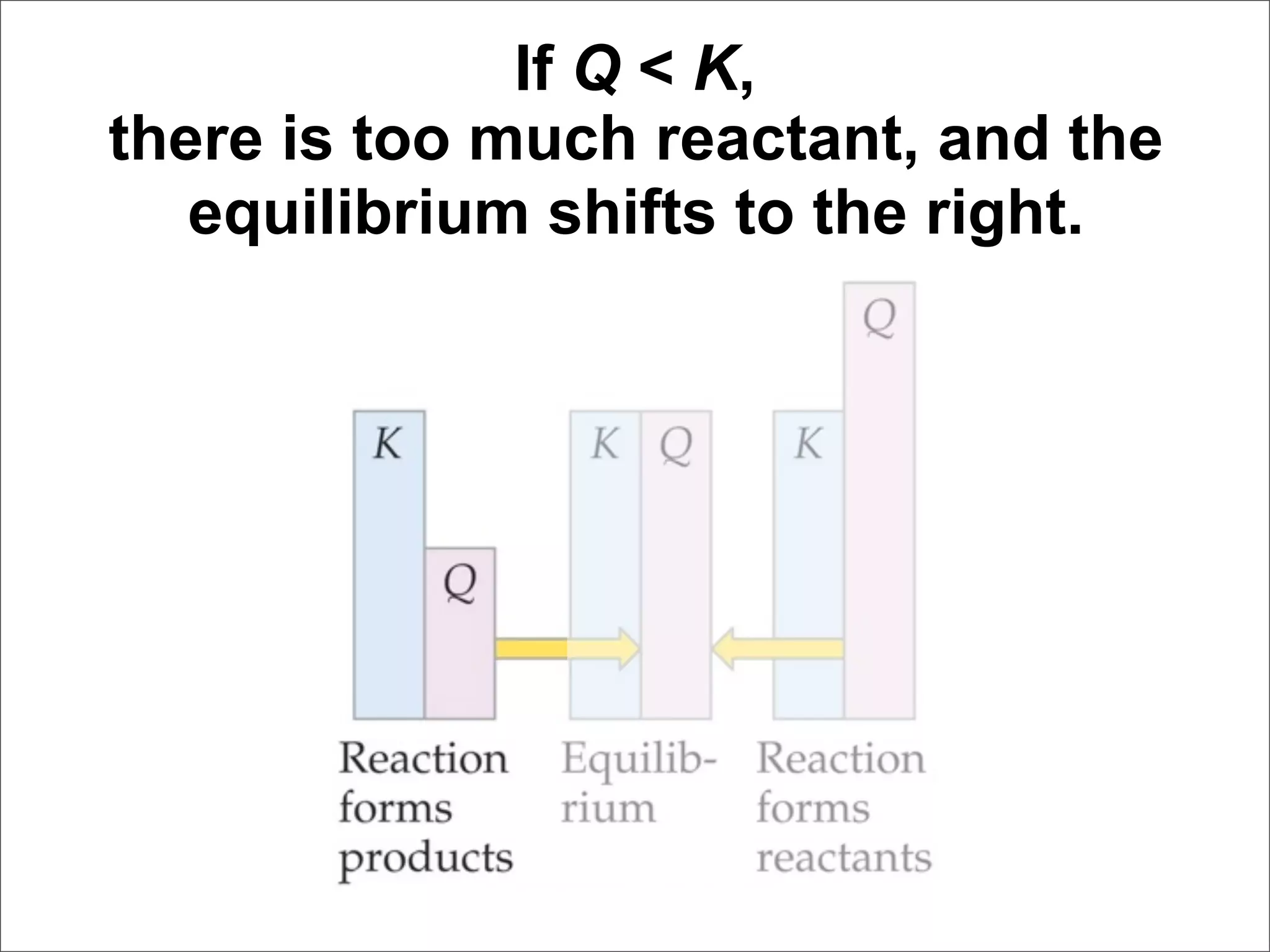
![For the following hypothetical reaction:
2 X(g) + Y(g) A(g)
Keq = 250. At a point during the reaction, the
concentrations are [A] = 1.0 M, [X] = 0.50 M,
and [Y] = 0.10 M. How will the reaction
proceed to achieve equilibrium?
1. From left to right (toward products)
2. From right to left (toward reactants)
3. Already at equilibrium](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-86-2048.jpg)
![Correct Answer:
1. From left to right (toward products)
2. From right to left (toward reactants)
3. Already at equilibrium
[ ]
1.0
Qc =
2
[0.50] [0.10]
Qc = 40
Because Qc < Keq, the reaction will shift from
reactants toward products to achieve equilibrium.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-87-2048.jpg)











![BELLWORK
Equilibrium is established between gases in the
reaction 2A(g) + 3B(g) ⇌ 1C(g) + 2D(g)
a) Write an expression for the equilibrium constant
b) What happens to the forward reaction rate if
more A is added? All reactants are involved in
the forward reaction’s rate law.
c) Would the equilibrium concentrations be the
same as they were before more A was added?
Explain.
d) Would [D] increase, decrease, or stay the same?](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-99-2048.jpg)
![a) [C][D]2
[A]2[B]3
b) Forward reaction rate increases if A is added
c) No, to keep K constant when more A is added,
new equilibrium concentrations will develop.
If all added A stays as A the ratio is “bottom heavy”.
If all added A reacts to form products the ratio is
“top heavy”
So SOME A will react to form products but not all.
All of the concentrations will change, the
amount of change will depend on K,
stoichiometry, and the amount of A added.
USE ICEBOX!
d) D will increase as more products are formed.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-100-2048.jpg)

















![Correct Answer:
1. From left to right (toward products)
2. From right to left (toward reactants)
3. No change in equilibrium
If [NH3] is decreased, to
return to equilibrium,
more NH3 must be
produced from the
reactants. Thus, the
reaction shifts from the
reactants to the
products.](https://image.slidesharecdn.com/15apequilibrium-100125074736-phpapp01/75/Chapter-15-Lecture-Chemical-Equilibrium-118-2048.jpg)