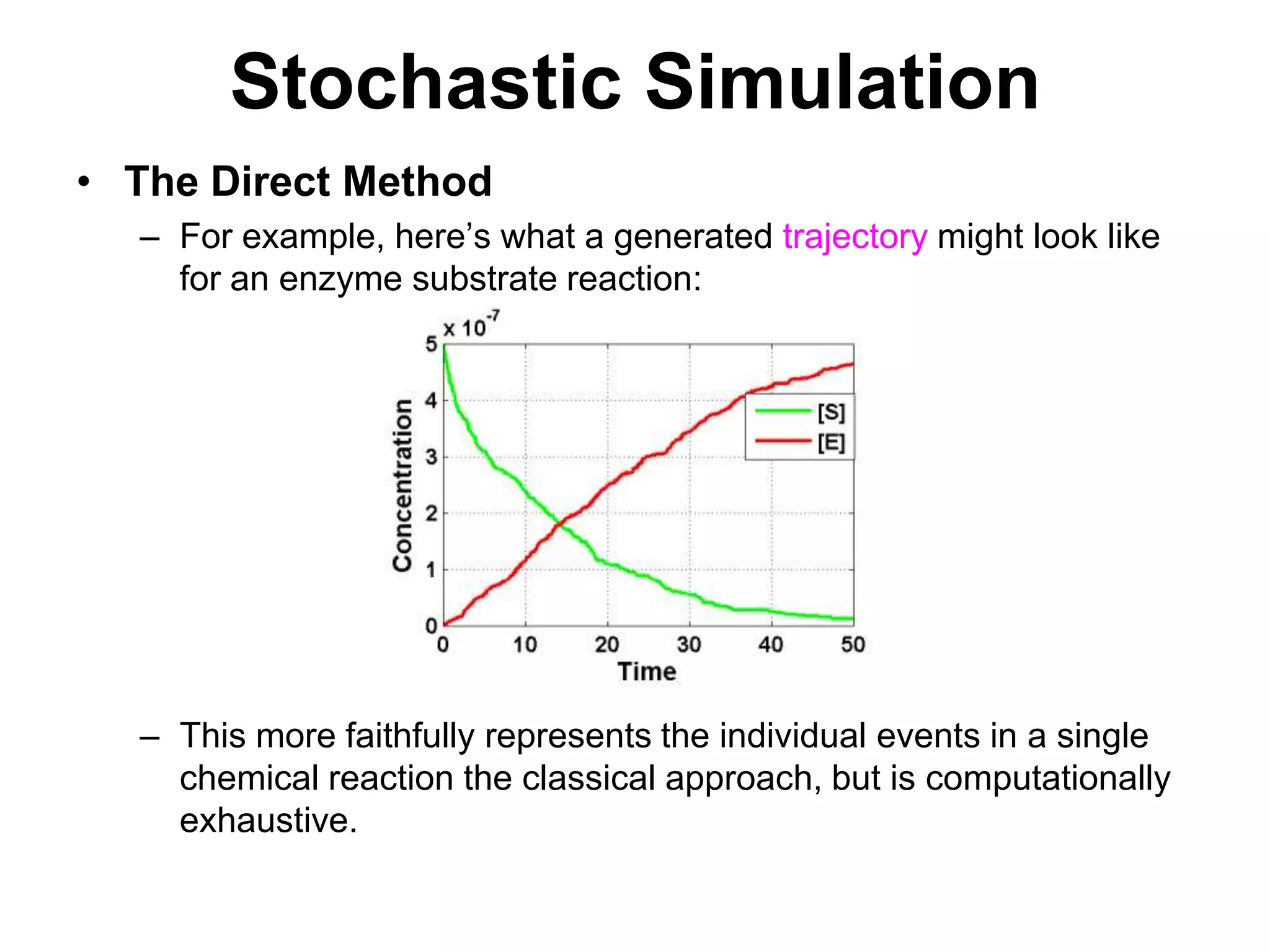
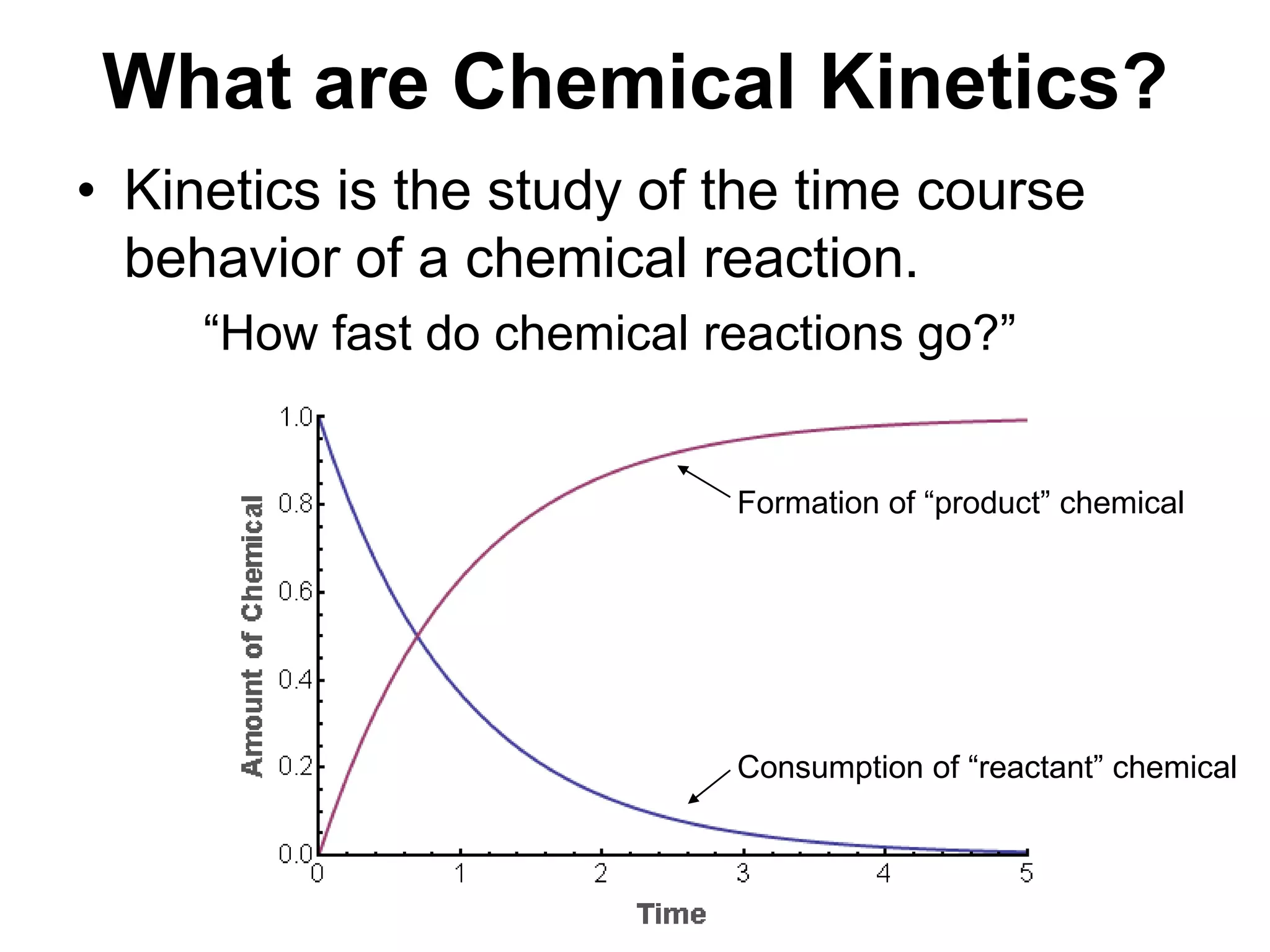
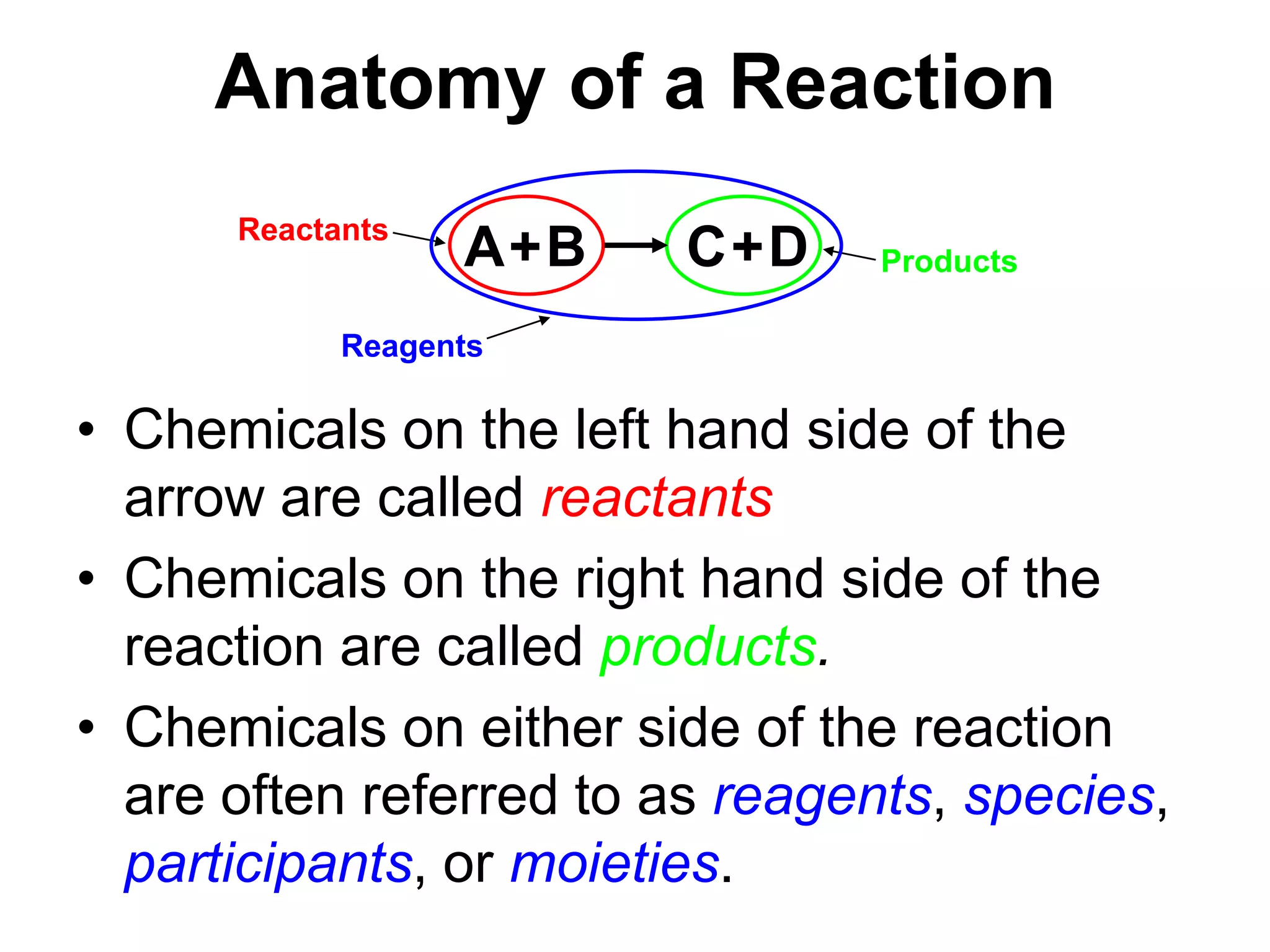
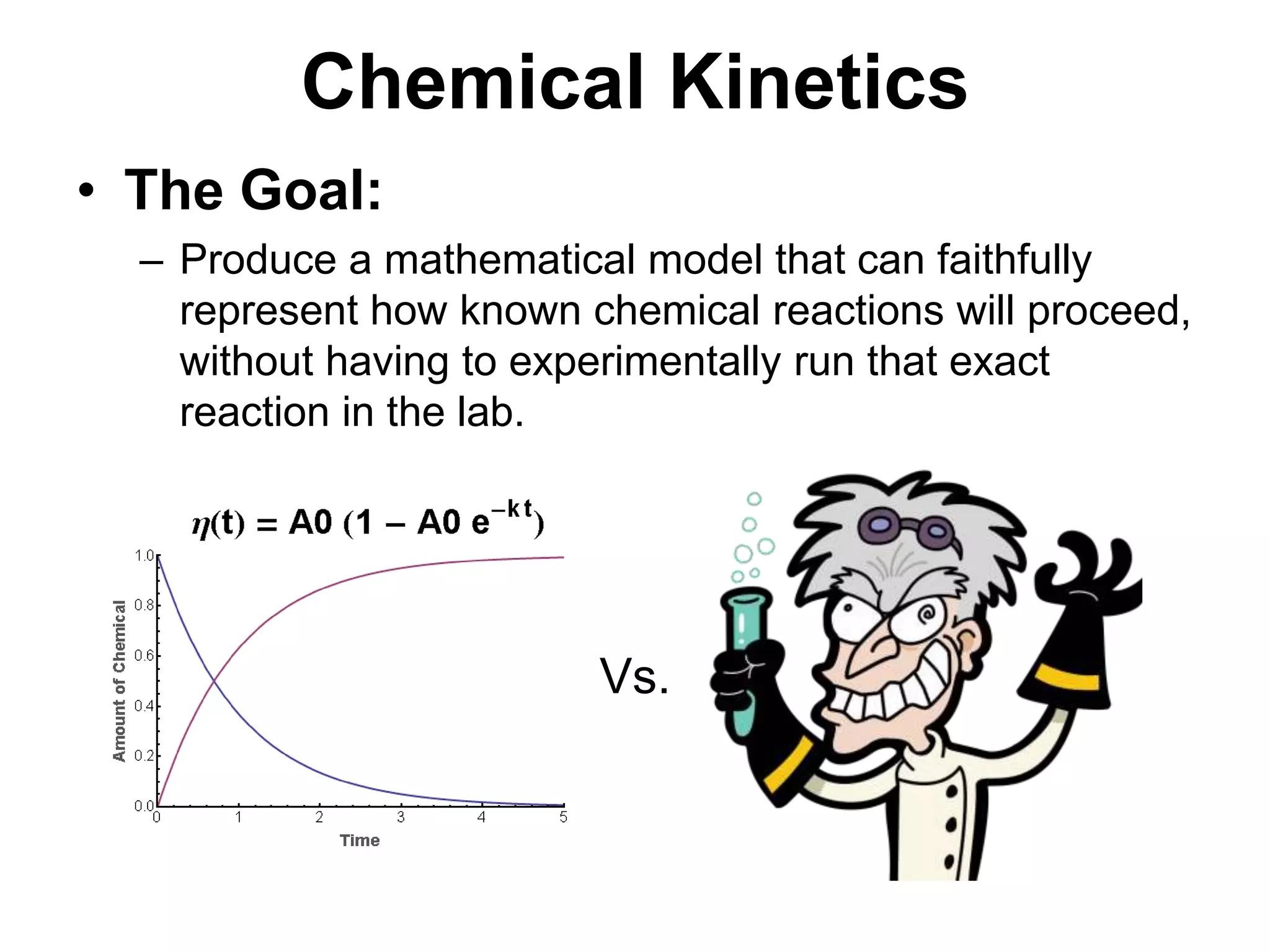
The document provides an overview of chemical kinetics, detailing the time course behavior of chemical reactions, including the significance of reaction rates, stoichiometric coefficients, and mass conservation principles. It discusses both phenomenological and stochastic approaches to modeling reactions, emphasizing the importance of mathematical models for predicting reaction behavior under various conditions. Additionally, the text covers key concepts like rate laws, reaction pathways, and the influence of reaction conditions on reaction kinetics.









![What are the Units?Amounts, or number of molecules of a chemical, are usually specified as Moles (mol) in multiples of Avogadro’s number which is roughly 6.022 x 1023 molecules per mol.A more relevant and commonly employed unit is concentration, or amount per volume. These are specified in Molar (M) and are in units of Moles/LiterSometimes square brackets around a name is used to denote concentration. Eg. [A] means the concentration of A.Both of these units are in metric, so prefixes like milli-(m), micro-(μor u), nano-(n) , etc. are commonly used shorthand for order of magnitude.](https://image.slidesharecdn.com/kineticsprimerv2-1-090928190224-phpapp02/75/Chemical-Kinetics-Made-Simple-12-2048.jpg)







![PhenomenologicalKineticsABExtent of ReactionSo for our example:Integrating and solving for [A]t and [B]t yields:Mass conservation:](https://image.slidesharecdn.com/kineticsprimerv2-1-090928190224-phpapp02/75/Chemical-Kinetics-Made-Simple-22-2048.jpg)





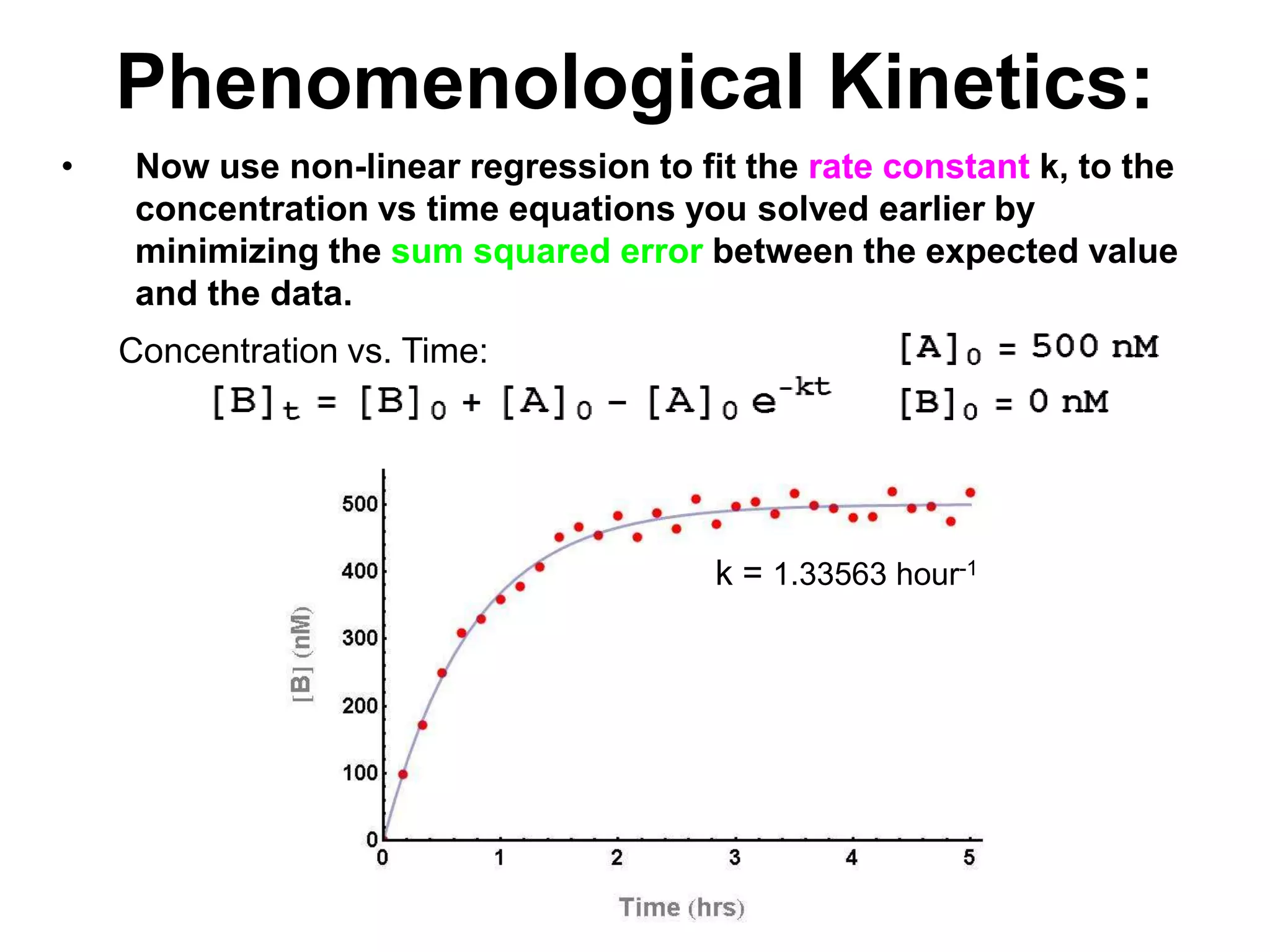
![PhenomenologicalKinetics:AB Victory! We can now simulate this particular reaction under any starting concentrations and couple it with any other reaction.wherek = 1.33563 hour-1[A]0 = 50nM[B]0 = 450nM[A]0 = 250nM[B]0 = 250nM[A]0 = 250nM[B]0 = 0nM](https://image.slidesharecdn.com/kineticsprimerv2-1-090928190224-phpapp02/75/Chemical-Kinetics-Made-Simple-29-2048.jpg)