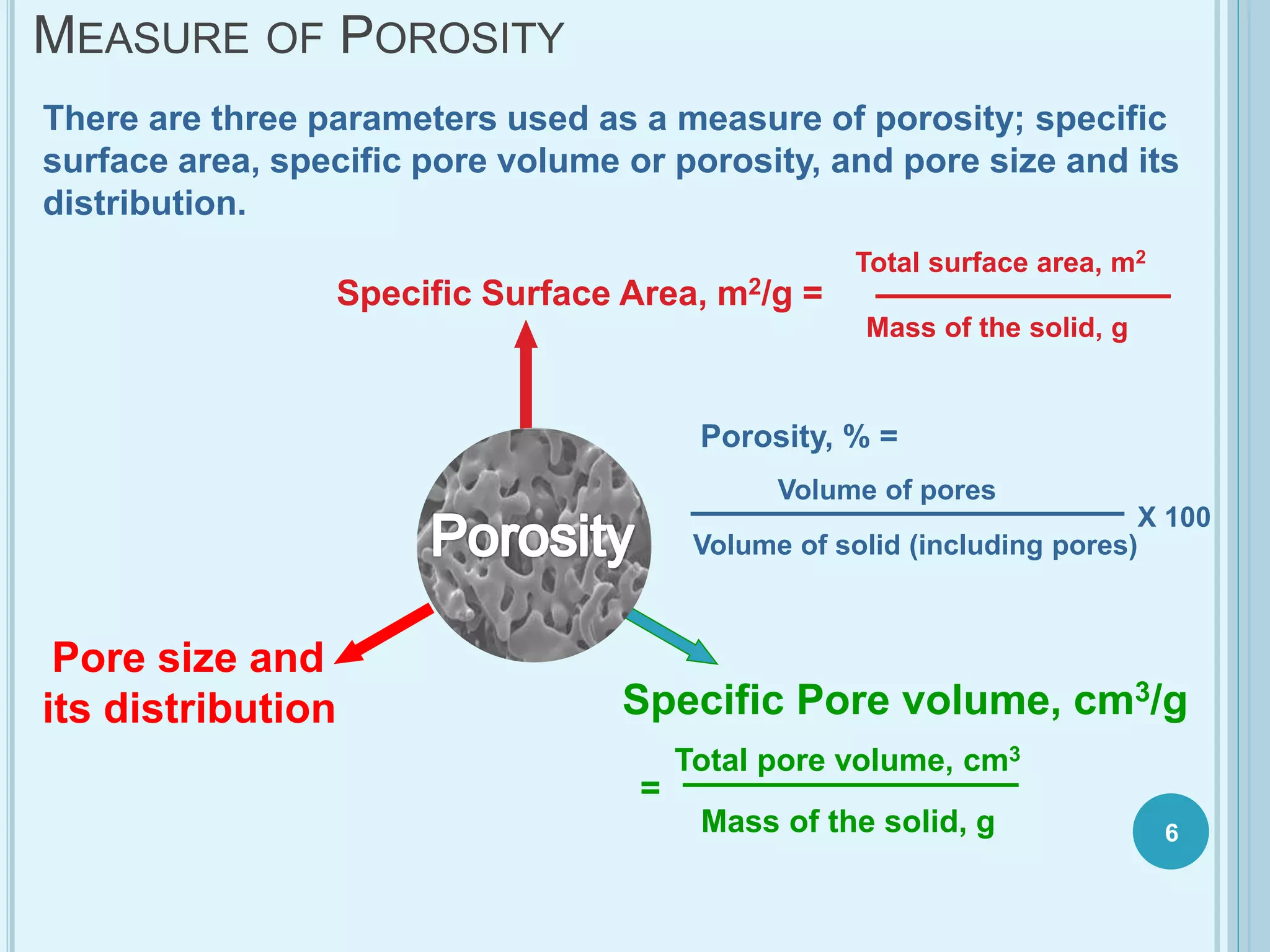
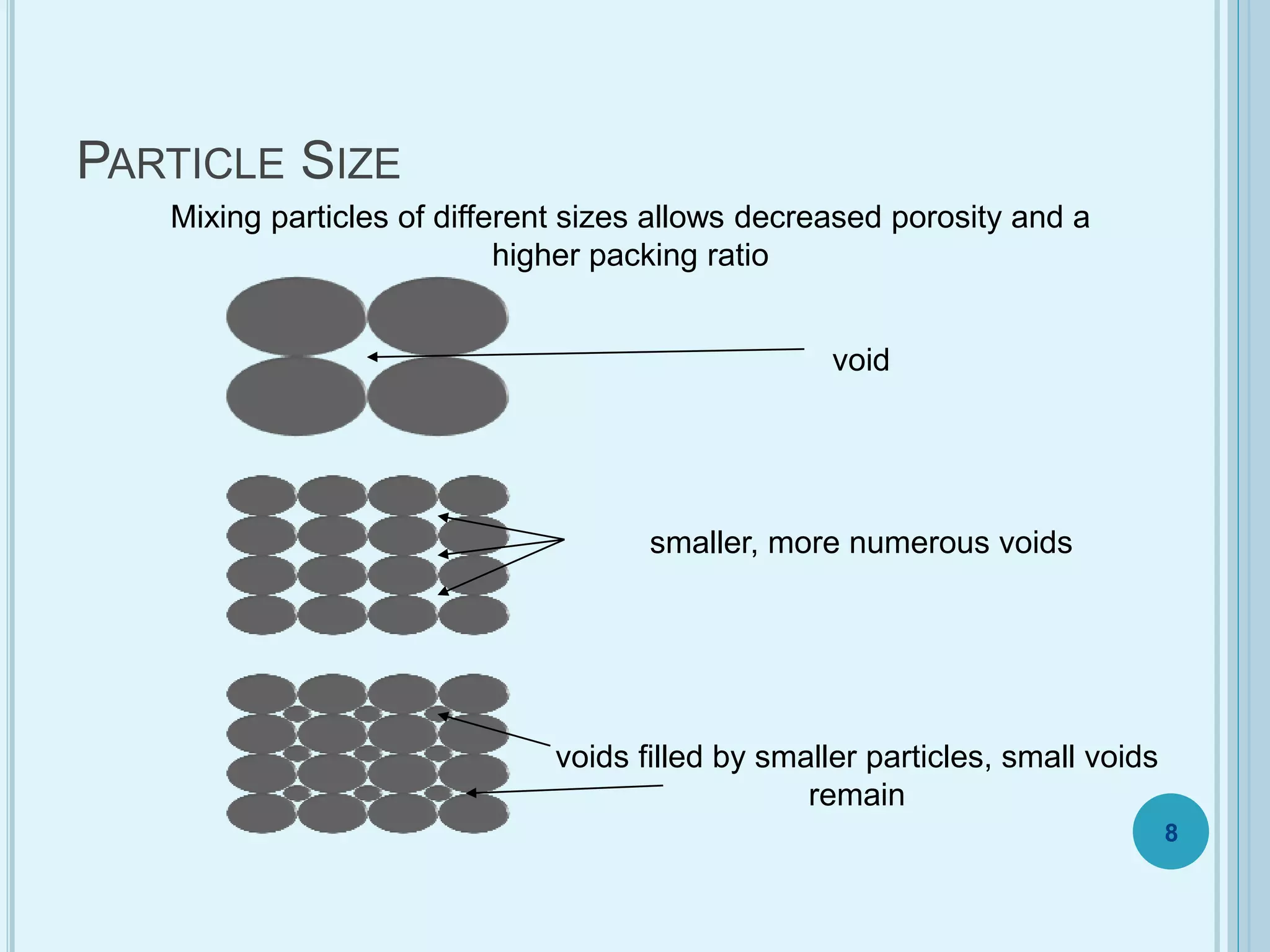
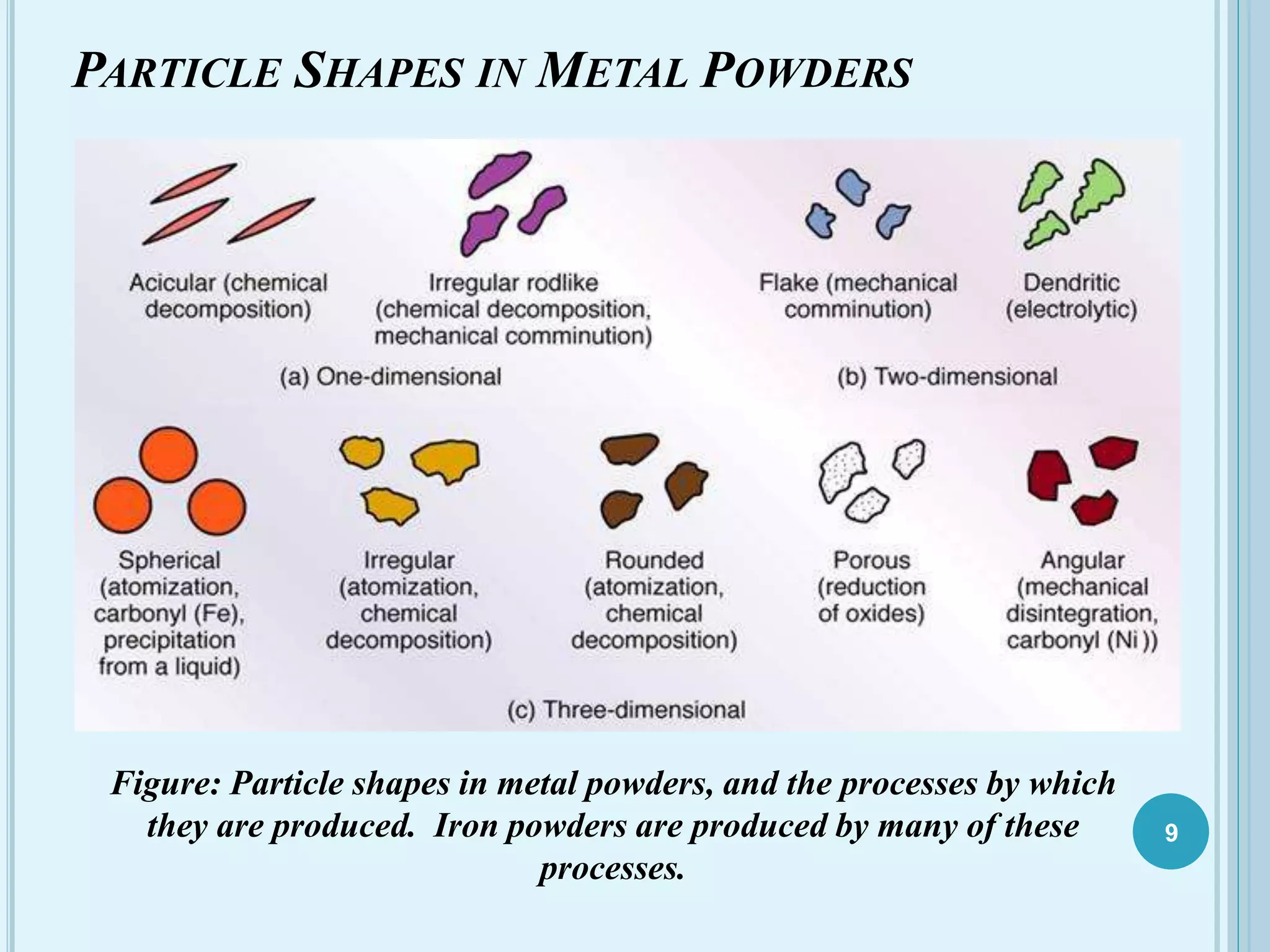
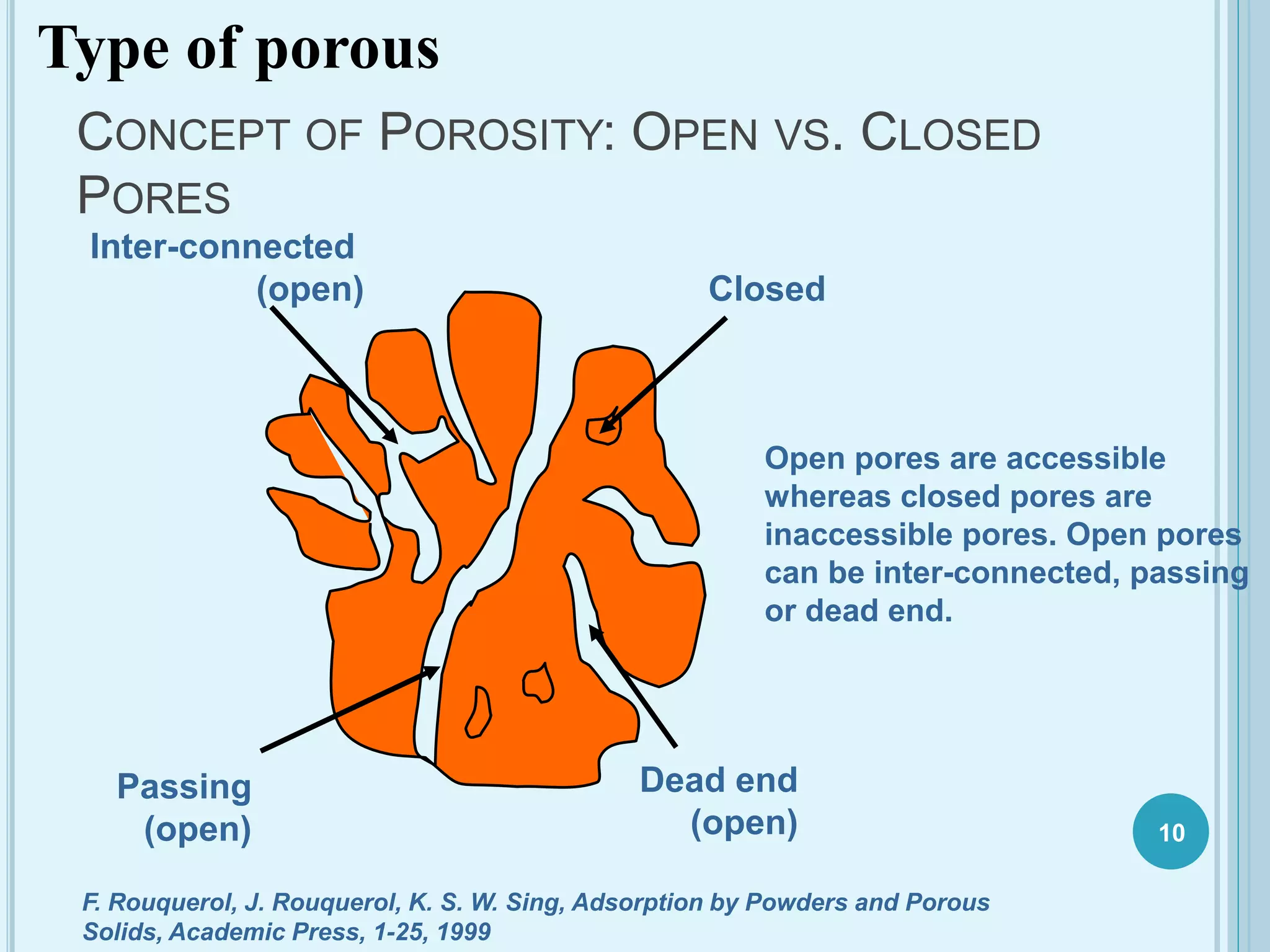
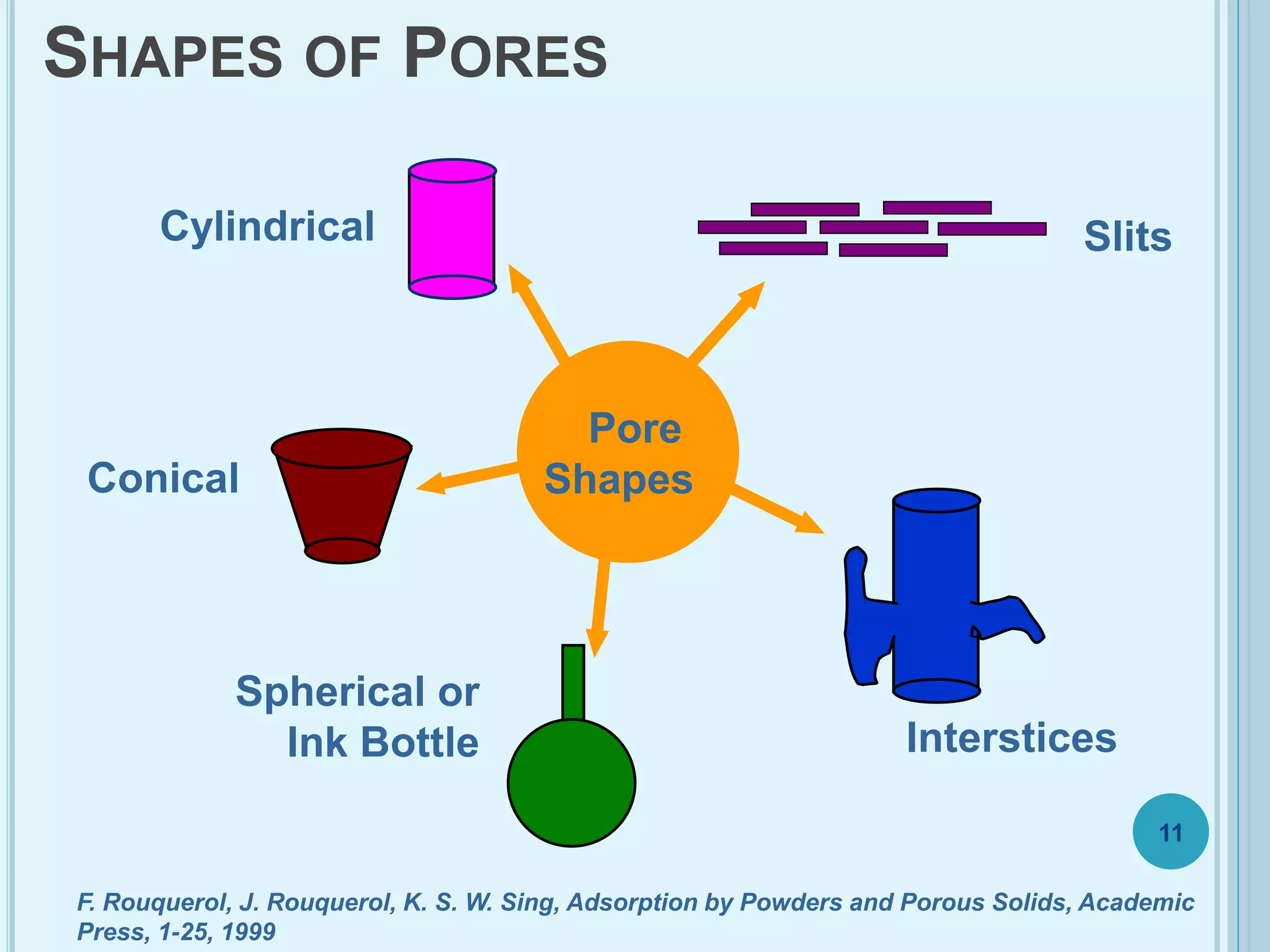
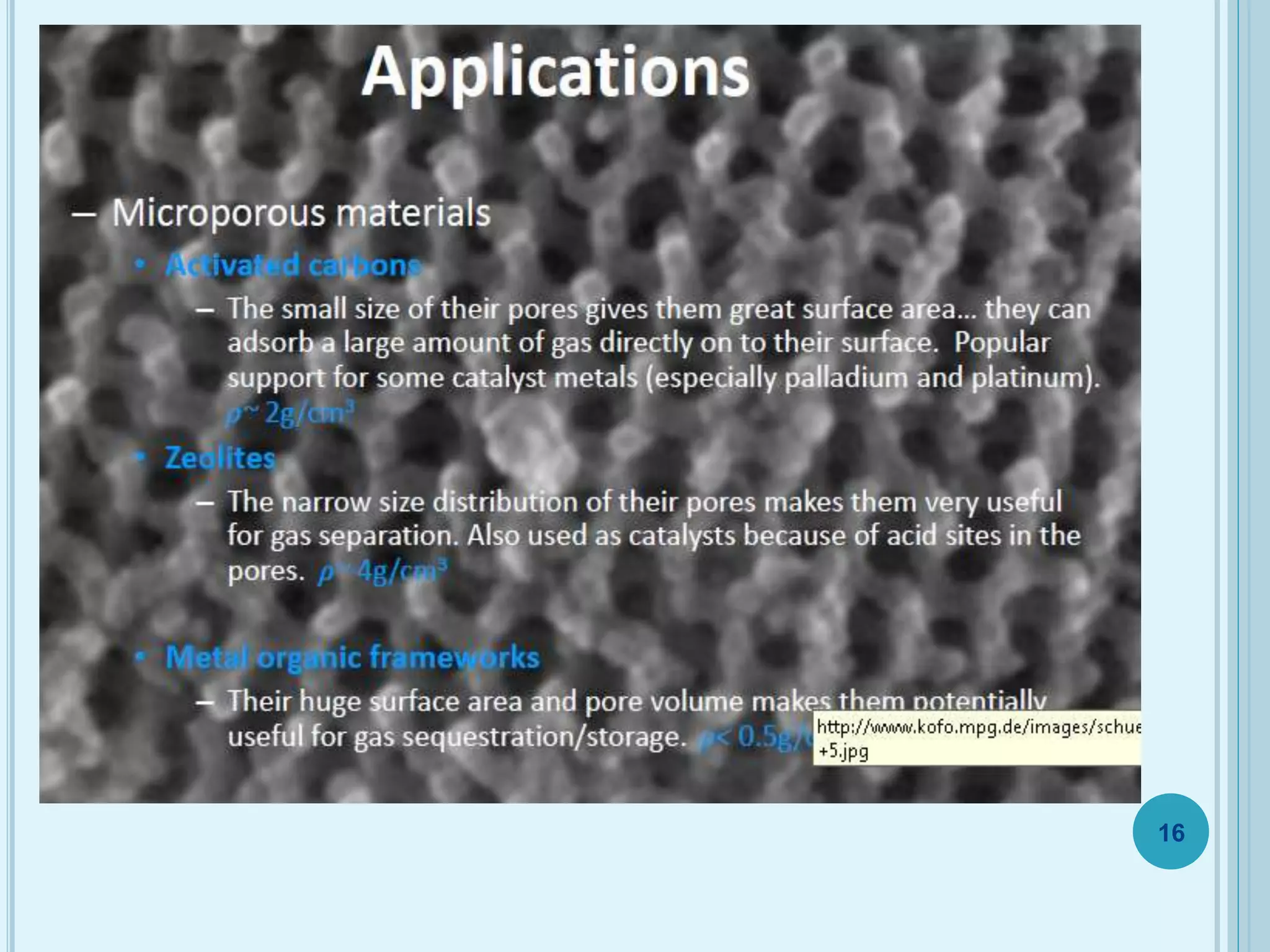
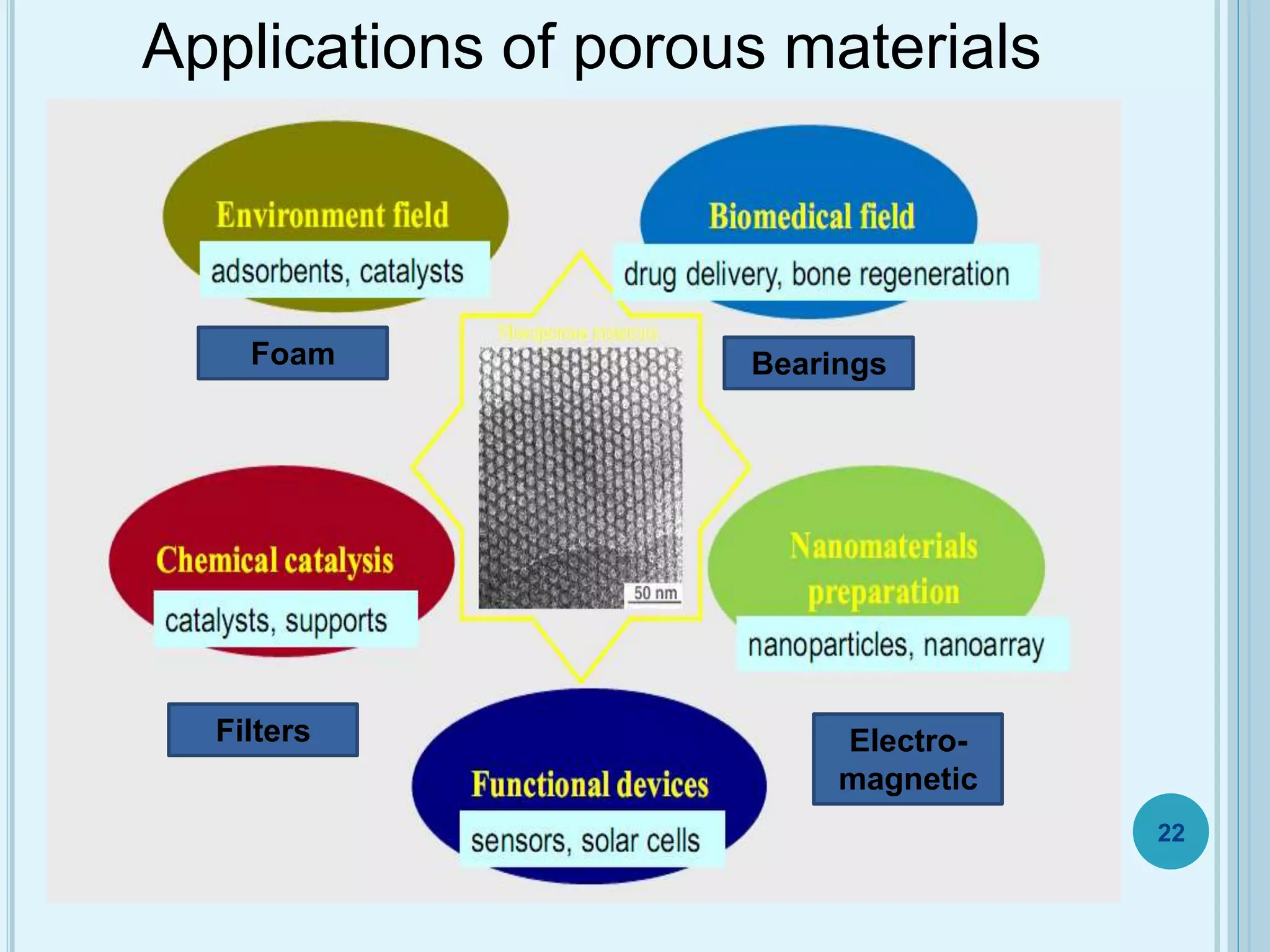
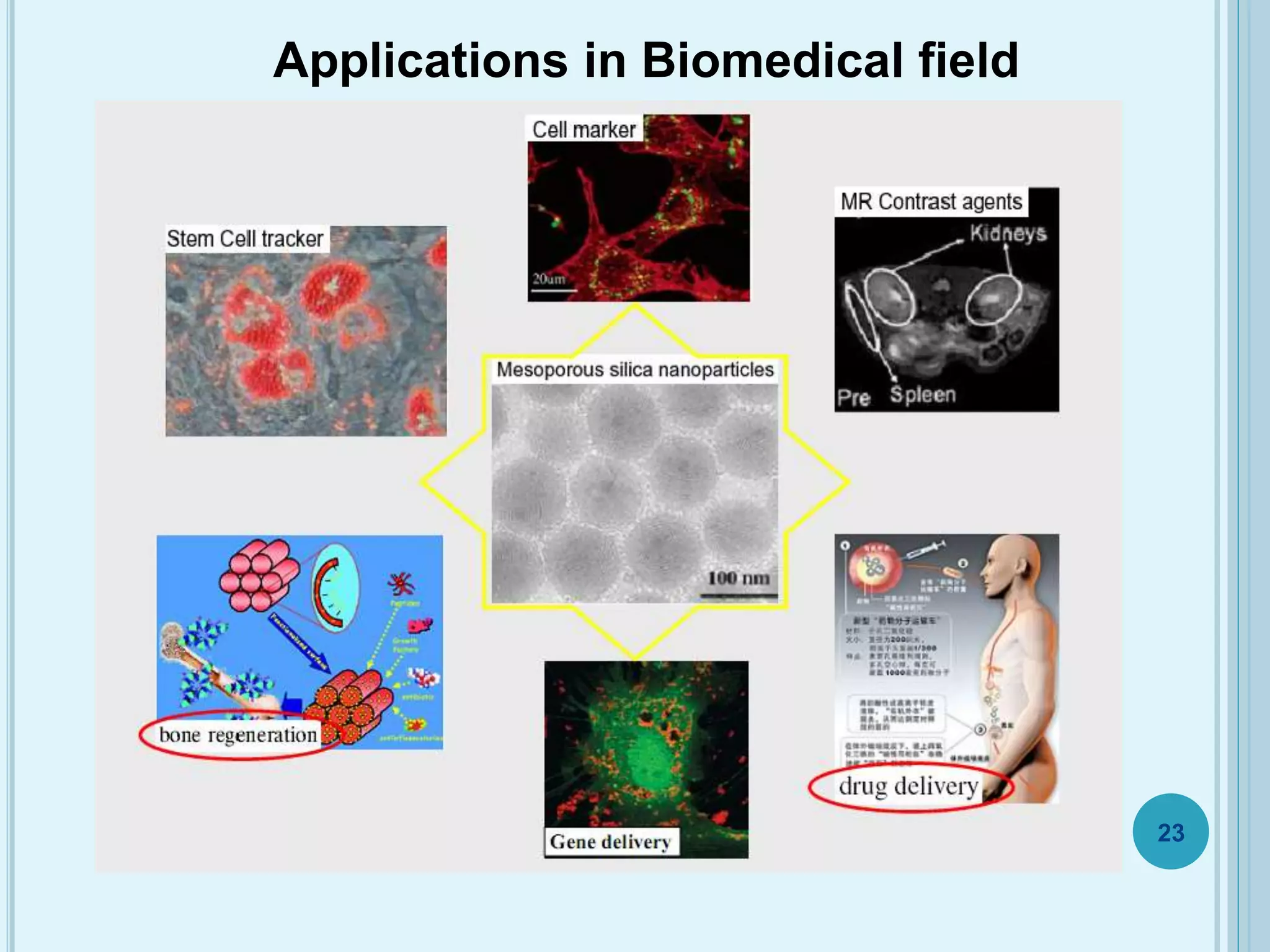
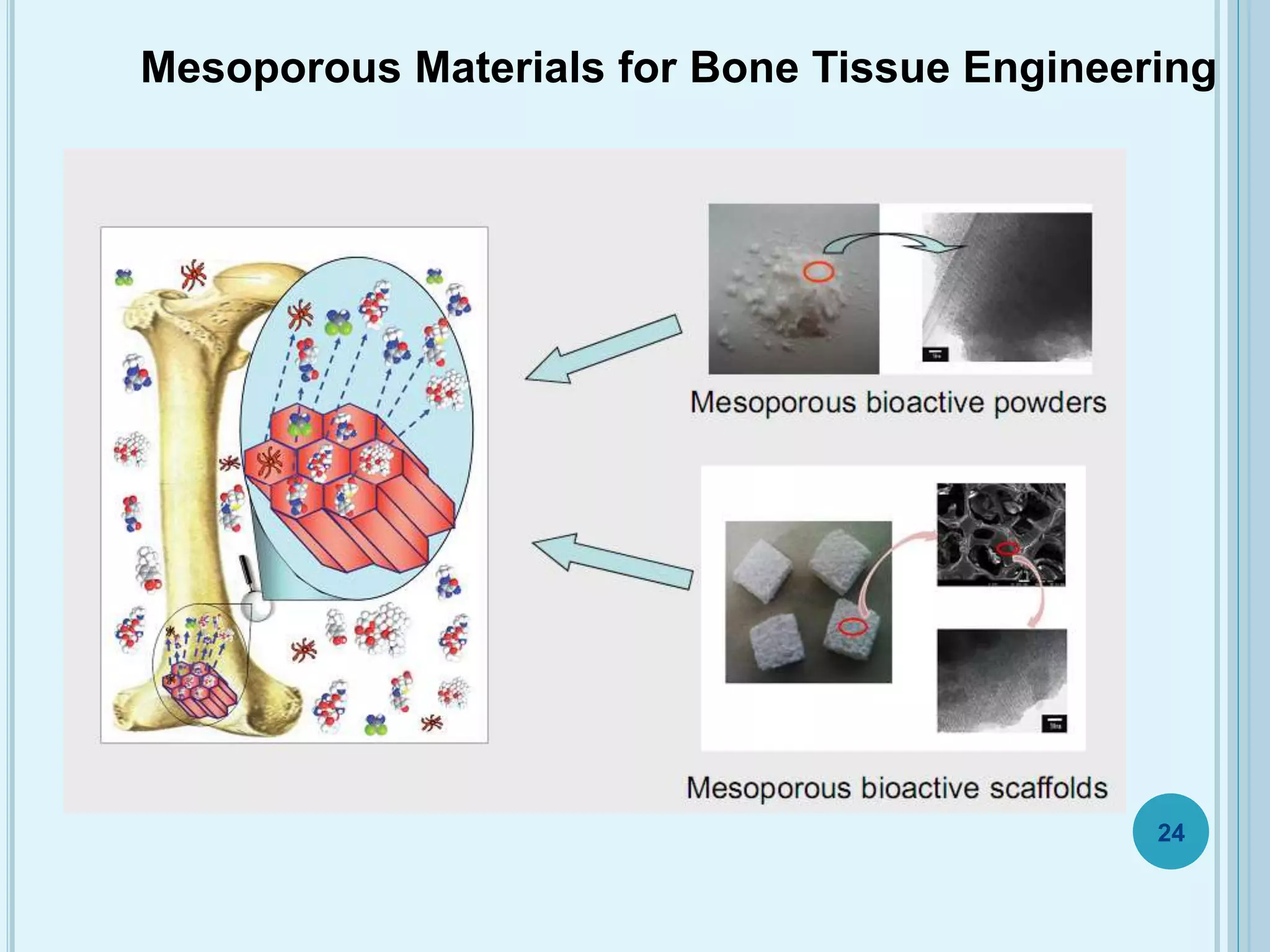
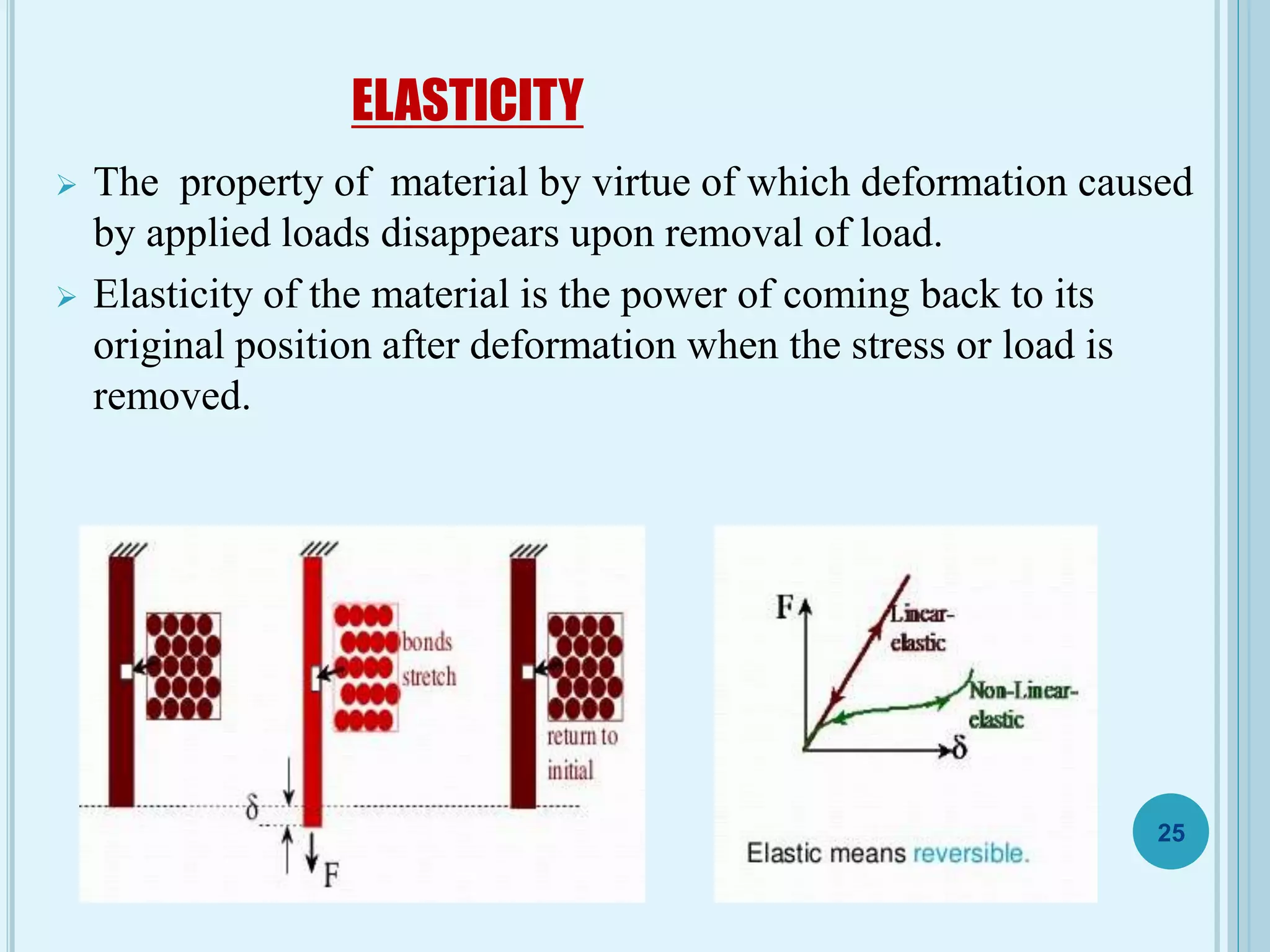
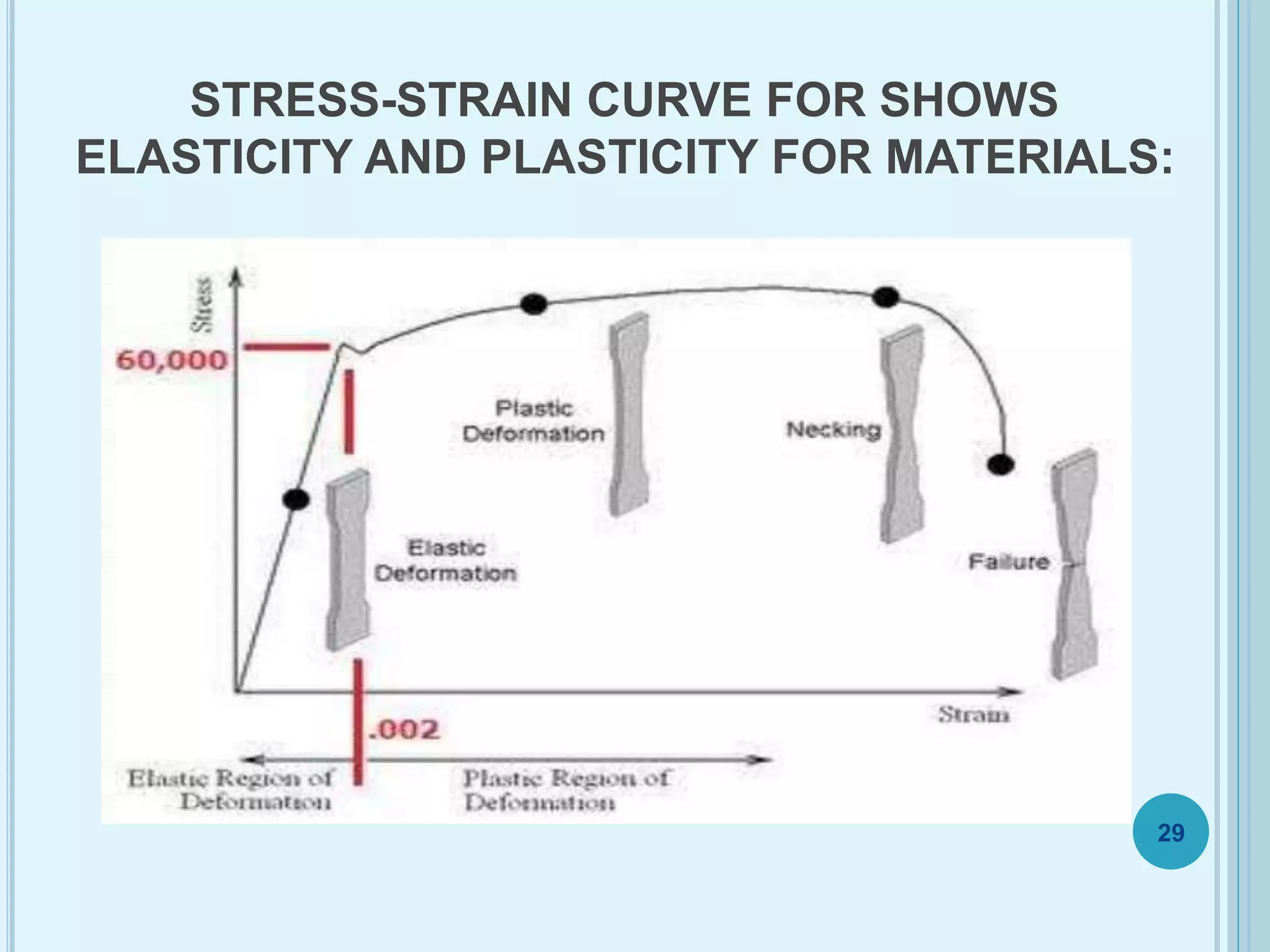
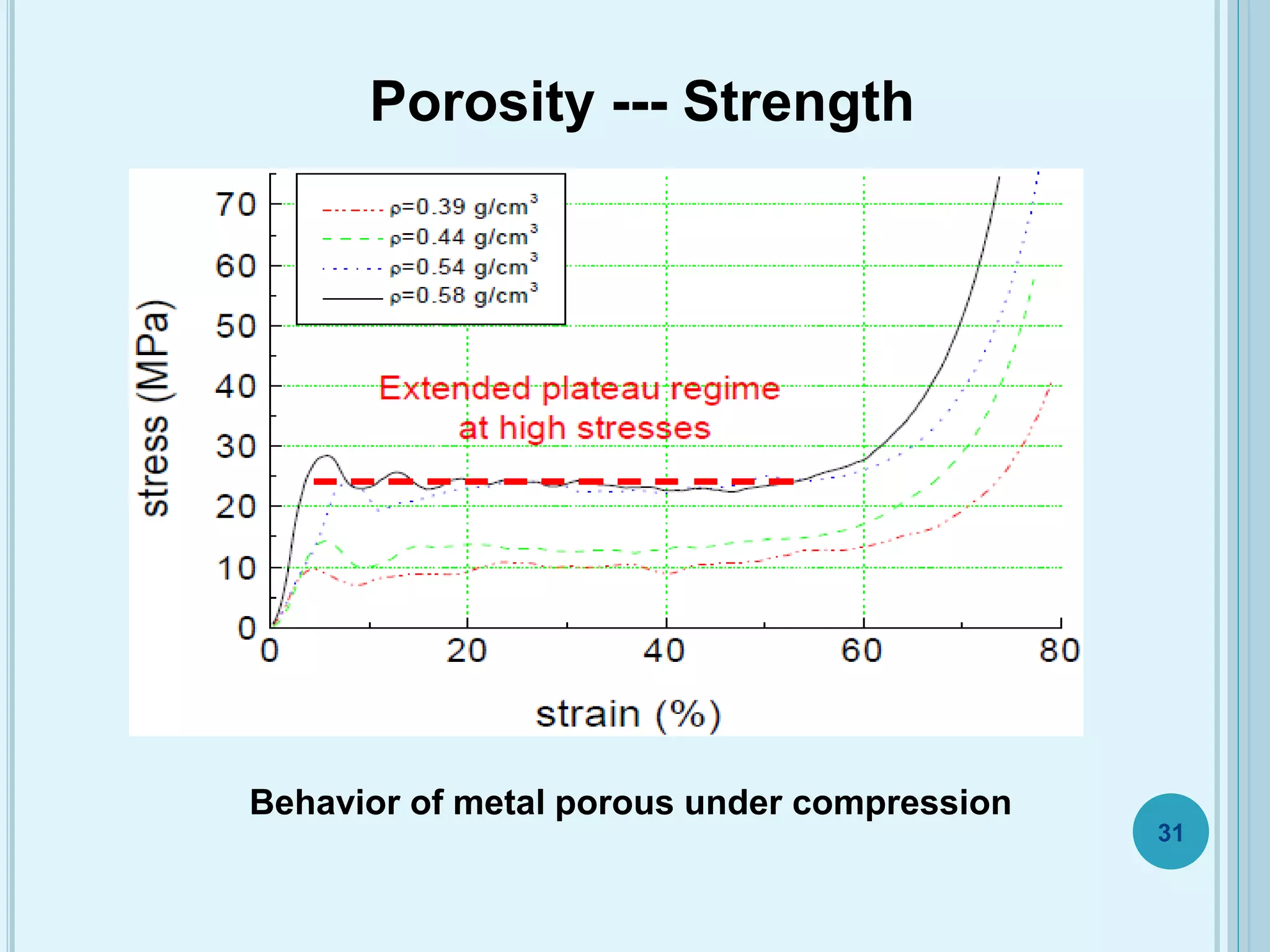
This document discusses plasticity theory related to porous materials. It begins with an introduction to porous materials, defining them as solids with high specific surface area and pore volume. Porosity is measured using specific surface area, specific pore volume, and pore size/distribution. Particle size, shape, and distribution affect porosity, with smaller, irregularly-shaped particles allowing for reduced porosity. Pores are classified as open or closed. Elasticity and plasticity in materials is also introduced, with plasticity defined as the ability to deform without failure. Porous metal plasticity models are discussed, intended for metals with over 90% density, based on void nucleation and failure. The effect of porosity on material strength is analyzed

1. Plasticity theory related to porous
materials
By
Bashar Ridha Younos Al-ogaidi
SUBMİTTED TO
Assistant Prof. ABDULLAH AKPOLAT
1

2. Introduction
Porous materials
Elasticity and plasticity
 summary
Contents
2

3. Introduction
Research in plasticity of porous materials has, at least,
a 40 year history. This research appears to have
proceeded in two primary directions:
(A) plasticity at small overall strains, in particular,
determination of the macroscopic yield surface in
stress space, accounting for porosity, in the cases
when such a surface can be clearly identified
and (B) void growth and coalescence at much larger
overall strains
3

4. 4

5. F. Rouquerol, J. Rouquerol, K. S. W. Sing, Adsorption by Powders and Porous
Solids, Academic Press, 1-25, 1999
WHAT ARE POROUS MATERIALS?
Non-porous solid
 Low specific surface area
 Low specific pore volume
Porous solid
 High specific surface area
 High specific pore volume
Porous materials have highly developed internal surface area that can be
used to perform specific function.
Almost all solids are porous except for ceramics fired at extremely high
temperatures
5

6. MEASURE OF POROSITY
Pore size and
its distribution
Specific Surface Area, m2/g =
There are three parameters used as a measure of porosity; specific
surface area, specific pore volume or porosity, and pore size and its
distribution.
Mass of the solid, g
Total surface area, m2
Specific Pore volume, cm3/g
Mass of the solid, g
Total pore volume, cm3
=
Porosity, % =
Volume of solid (including pores)
Volume of pores
X 100
6

7. Parameters that effected on porousity :-
1- partical size
2- partical shape
3- partical ditripution
7

8. PARTICLE SIZE
void
smaller, more numerous voids
voids filled by smaller particles, small voids
remain
Mixing particles of different sizes allows decreased porosity and a
higher packing ratio
8

9. PARTICLE SHAPES IN METAL POWDERS
9
Figure: Particle shapes in metal powders, and the processes by which
they are produced. Iron powders are produced by many of these
processes.

10. CONCEPT OF POROSITY: OPEN VS. CLOSED
PORES
Dead end
(open)
Closed
Inter-connected
(open)
Passing
(open)
F. Rouquerol, J. Rouquerol, K. S. W. Sing, Adsorption by Powders and Porous
Solids, Academic Press, 1-25, 1999
Open pores are accessible
whereas closed pores are
inaccessible pores. Open pores
can be inter-connected, passing
or dead end.
Type of porous
10

11. SHAPES OF PORES
Conical
Interstices
SlitsCylindrical
Spherical or
Ink Bottle
Pore
Shapes
F. Rouquerol, J. Rouquerol, K. S. W. Sing, Adsorption by Powders and Porous Solids, Academic
Press, 1-25, 1999
11

12. PROPERTIES OF POROUS METALS
 Lightweight structure
 Energy absorber
 High temperature resistant
 Heat exchanger
 Biomaterial
 Filter
12

13. ADVANTAGES OF FORMING OF POROUS METALS
 Forming to desired shape
 Control of porosity and morphology
 Work hardening of matrix
 Improvements in properties
 Unusual microstructure
 Forming of complicated shapes
13

14. SIZE OF PORES (IUPAC STANDARD)
2 nm 50 nm
Micropores Mesopores Macropores
Zeolite,
Activated
carbon,
Metal organic
framework
Mesoporous silica,
Activated carbon Sintered metals
and ceramics
Porous material are classified according to the size of pores: material with
pores less than 2 nm are called micropores, materials with pores between 2
and 50 nm are called mesopores, and material with pores greater than 50
nm are macrospores
Sing, K. S. W. et al. Reporting Physisorption Data for Gas/Solid Systems. Pure & Appl. Chem. 57,
603-619 (1985).
14

15. 15

16. 16

17. 17

18. 18

19. 19

20. 20

21. 21

22. Applications of porous materials
BearingsFoam
Filters Electro-
magnetic
22

23. Applications in Biomedical field
23

24. Mesoporous Materials for Bone Tissue Engineering
24

25. ELASTICITY
 The property of material by virtue of which deformation caused
by applied loads disappears upon removal of load.
 Elasticity of the material is the power of coming back to its
original position after deformation when the stress or load is
removed.
25

26.  The physical reasons for elastic behavior can be quite
different for different materials. In metals, the atomic
lattice changes size and shape when forces are applied
(energy is added to the system). When forces are
removed, the lattice goes back to the original lower
energy state.
 In engineering, the amount of elasticity of a material
is determined by two types of material parameter.
 The first type of material parameter is called
a modulus, which measures the amount of force per
unit area (stress) needed to achieve a given amount of
deformation. The units of modulus are pascals (Pa).
 A higher modulus typically indicates that the material
is harder to deform. 26

27.  The second type of parameter measures the elastic
limit. The limit can be a stress beyond which the
material no longer behaves elastic and deformation of
the material will take place.
 If the stress is released, the material will elastically
return to a permanent deformed shape instead of the
original shape.
27

28. PLASTICITY:
 The plasticity of a material is its ability to undergo
some degree of permanent deformation without rupture
or failure.
 Plastic deformation will take only after the elastic limit
is exceeded.
 It increases with increase in temperature.
28

29. STRESS-STRAIN CURVE FOR SHOWS
ELASTICITY AND PLASTICITY FOR MATERIALS:
29

30. Porous metal plasticity
– The porous metal plasticity model is intended for
metals with relative densities greater than 90% (i.e.,
a dilute concentration of voids).
– The model is based on Gurson’s porous plasticity
model with void nucleation and failure.
– Inelastic flow is based on a potential function which
characterizes the porosity in terms of a single state
variable—the relative density.
– The model is well-tuned for tensile applications,
such as fracture studies with void coalescence, but
it is also useful for compressive cases where the
material densifies.
– The details of this material model are discussed in
the Metal Inelasticity in ABAQUS lecture notes.
30

31. Porosity --- Strength
Behavior of metal porous under compression
31

32. 32

33. 33

34. The effect of porosity on strength during densification by preform working
can be analyzed using a simple model. Consider an ideal porous material
of relative strength στ as defined by Haynes (1970):
σχ = σ/σ0 = (1 - ρ) (1)
where σ is the true stress for flow of the porous preform at a specified level of
strain, σ0 the true stress for flow of the fully dense material at the same level
of strain, and ρ the percent porosity. In a real (nonideal) situation, the pores
give rise to local stress concentrations in addition to reducing the effective
load-bearing cross section. If the stress concentration factor due to pores is
Kp, Eq. (1) is modified into
σχ = σ/σ0 = (1 - p)/Kp (2)
34

35.  II. PLASTİC DEFORMATION OF SINTERED POWDER
METAL
 1.Physical Model
 Investigation of densification of a porous metal is
facilitated by consideration of deformation of a material
element containing a void. It is well known from plasticity
analysis of a thick-walled sphere that it is impossible to
completely colose a hole by hydrostatic pressure of finite
magnitute. The pressure repuired for plastic deformation of
a sphere containing a hole is given by
35

36.  where σ0 is the flow stress of the material, r0 the
outside radius (equivalent to mean space between
voids), and ri is the hole radius (equivalent to void
radius). It is clear that voids of large diameter (large
ri ) require less pressure for densification than
small voids, and that, as the void diameter
approaches zero, the pressure required for
densification becomes unbounded. Under
hydrostatic pressure, the void simply changes size,
but not shape, since the pressure is equal in all
directions.
36

37. 37

38. 38
000

39. 39

40. 40

41. THANK YOU FOR
YOUR ATTENTION
41