More Related Content
PPTX
PPTX
PPTX
PPTX
PPTX
PDF
PPTX
PDF
データサイエンス概論第一=8 パターン認識と深層学習 What's hot
PPTX
PPTX
強化学習エージェントの内発的動機付けによる探索とその応用(第4回 統計・機械学習若手シンポジウム 招待公演) PDF
PDF
最近のKaggleに学ぶテーブルデータの特徴量エンジニアリング PPTX
PDF
PDF
統計的学習理論チュートリアル: 基礎から応用まで (Ibis2012) PDF
PPTX
データサイエンス概論第一=1-2 データのベクトル表現と集合 PPTX
【DL輪読会】ViT + Self Supervised Learningまとめ PDF
PPTX
PDF
ゼロから始める深層強化学習(NLP2018講演資料)/ Introduction of Deep Reinforcement Learning PDF
PDF
PDF
PDF
Visualizing Data Using t-SNE PPTX
データサイエンス概論第一=2-1 データ間の距離と類似度 PPTX
データサイエンス概論第一=3-2 主成分分析と因子分析 PPTX
Swin Transformer (ICCV'21 Best Paper) を完璧に理解する資料 Similar to 統計分析
PDF
PDF
PDF
PDF
PDF
PDF
2022年度秋学期 統計学 第11回 分布の「型」を考える - 確率分布モデルと正規分布 (2022. 12. 6) PDF
2014年度春学期 統計学 第11回 分布の推測とはー分布の「型」を考える - 確率分布モデルと正規分布 (2014. 6. 26) PPTX
PDF
2015年度春学期 統計学 第11回 分布の「型」を考える - 確率分布モデルと正規分布 (2015. 6. 25) PDF
2015年度秋学期 統計学 第11回 分布の「型」を考える - 確率分布モデルと正規分布 (2015. 12. 9) PDF
2013年度秋学期 統計学 第11回「分布の「型」を考える - 確率分布モデルと正規分布」 PDF
2021年度秋学期 統計学 第11回 分布の「型」を考える ー 確率分布モデルと正規分布(2021. 12. 7) PDF
2020年度秋学期 統計学 第11回 分布の「型」を考えるー確率分布モデルと正規分布 (2020. 12. 8) PPTX
データサイエンス概論第一=4-1 相関・頻度・ヒストグラム PPTX
PDF
PDF
PDF
2022年度秋学期 統計学 第10回 分布の推測とはー標本調査,度数分布と確率分布 (2022. 11. 29) PDF
2022年度春学期 統計学 第11回 分布の「型」を考えるー確率分布モデルと正規分布 PDF
2014年度秋学期 統計学 第14回 分布についての仮説を検証する ― 仮説検定 (2015. 1. 14) 



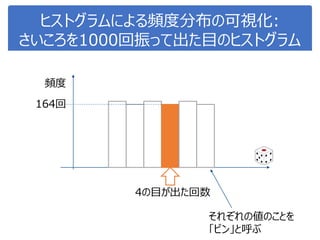

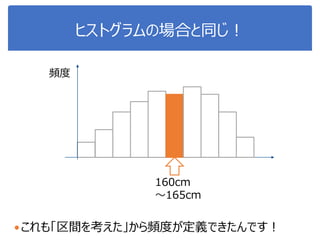
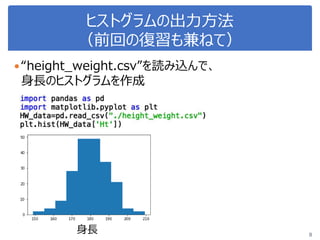
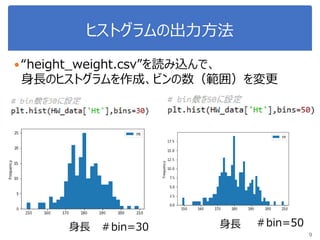



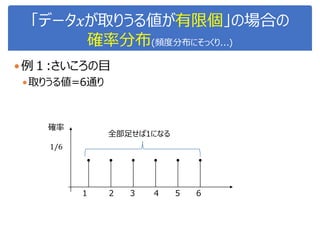
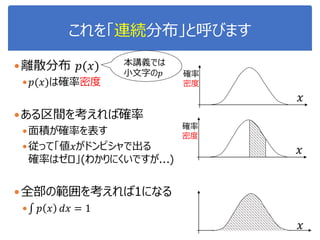
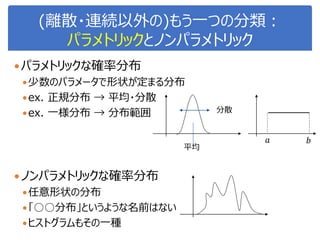
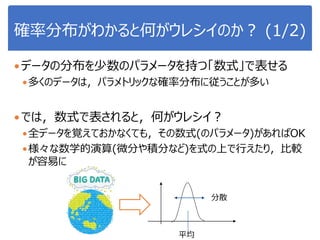
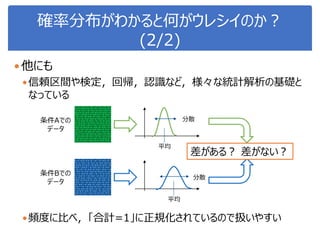

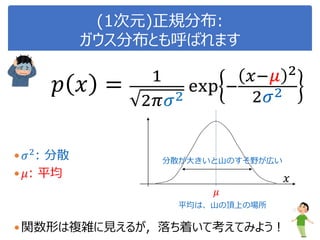
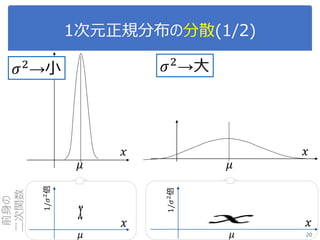
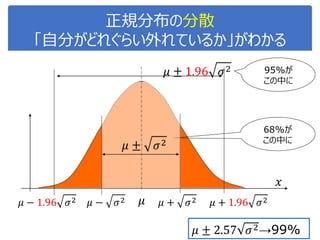
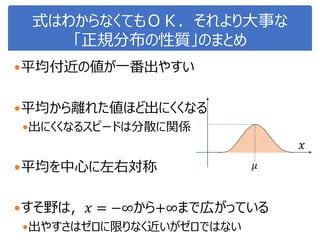

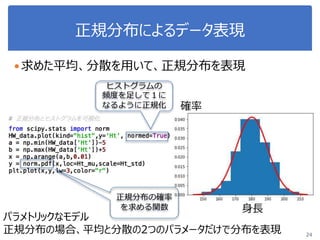


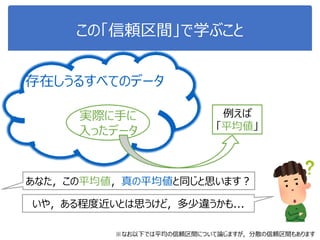
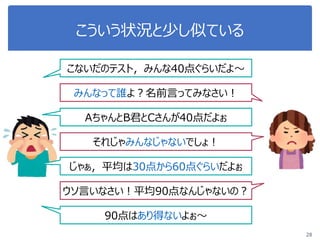

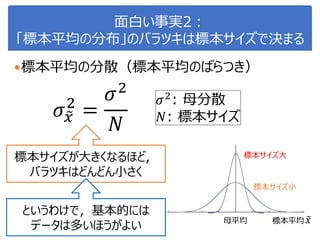

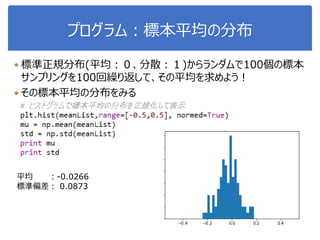



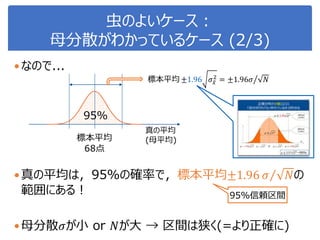
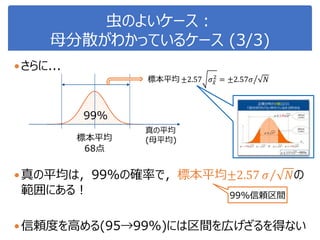
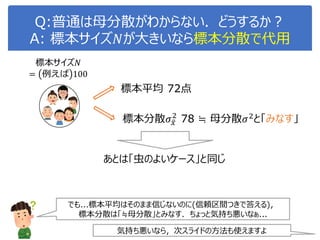
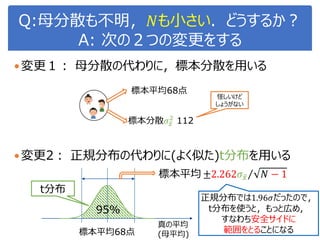
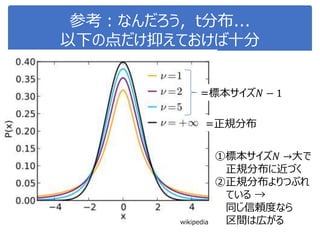
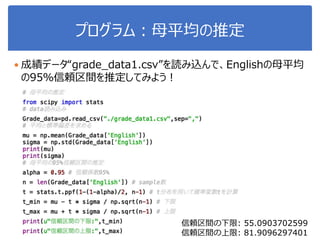










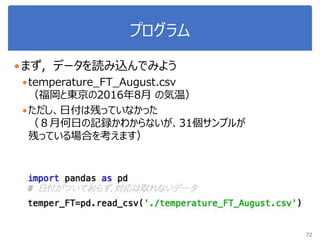
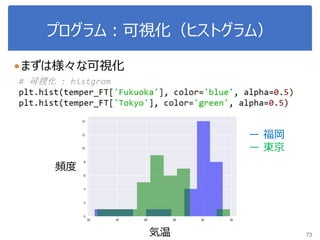
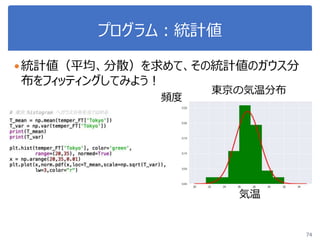






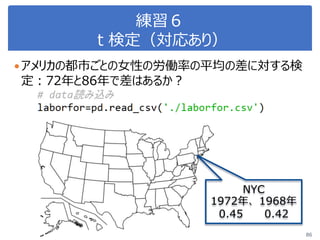

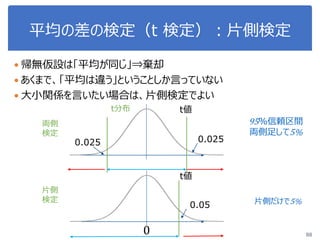
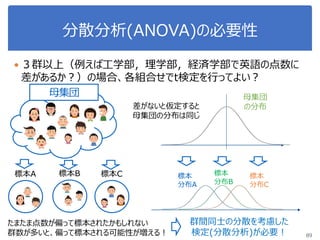




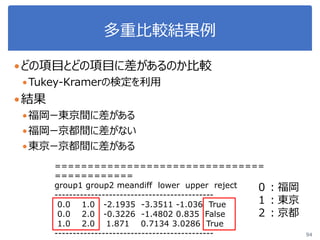
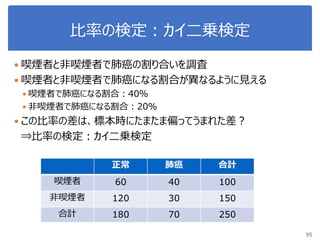
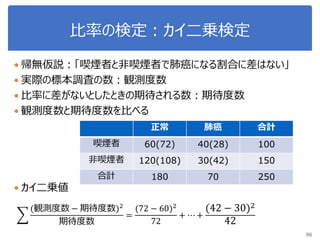
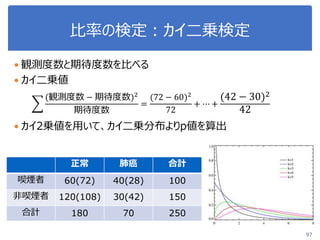
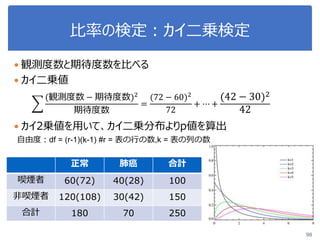






![演習1-3:クラスごとに可視化
105
petal-lengthは、2つの分布があるように見える
⇒クラスに分けてヒストグラム及び正規分布で表現
ヒント
クラスごとに分類
irisSetosa = iris[iris.iloc[:,2]=='Iris-setosa']
irisVersicolor = iris[iris.iloc[:,2]=='Iris-versicolor']
irisVirginica = iris[iris.iloc[:,2]=='Iris-virginica']](https://image.slidesharecdn.com/statisticalanalysis-190124093721/85/slide-105-320.jpg)
![演習1-4:母平均の信頼区間の推定
106
“iris_2metrics2.csv”を読み込んで、sepal-lengthの母平均の
95%信頼区間を推定せよ
ヒント
信頼区間の求め方
alpha = 0.95 # 信頼係数95%
n = len(iris['sepal-length']) # sample数
t = stats.t.ppf(1-(1-alpha)/2, n-1) # t分布を用いて確率変数tを計算
t_min = mu - t * sigma / np.sqrt(n-1) # 下限
t_max = mu + t * sigma / np.sqrt(n-1) # 上限](https://image.slidesharecdn.com/statisticalanalysis-190124093721/85/slide-106-320.jpg)

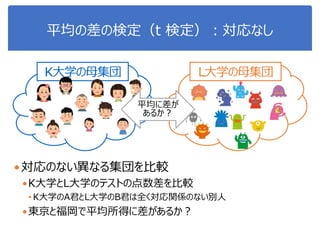
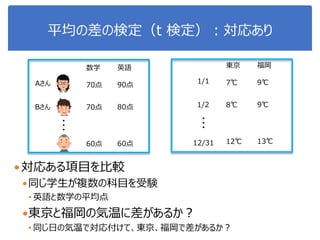
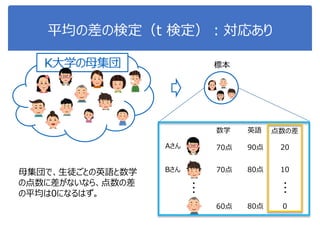
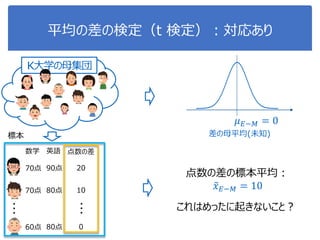
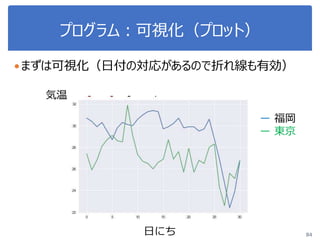
![演習1-6:平均の差の検定
108
クラスを分けて、それぞれsepal-lengthとpetal-lengthの差を
棄却域5%で検定せよ
ヒント
from scipy import stats
t, p = stats.ttest_ind(データA, データB, equal_var=False)
クラスごとに分類
irisSetosa = iris[iris.iloc[:,2]=='Iris-setosa']
irisVersicolor = iris[iris.iloc[:,2]=='Iris-versicolor']
irisVirginica = iris[iris.iloc[:,2]=='Iris-virginica']](https://image.slidesharecdn.com/statisticalanalysis-190124093721/85/slide-108-320.jpg)

