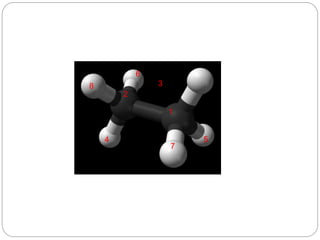
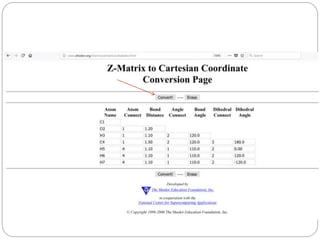
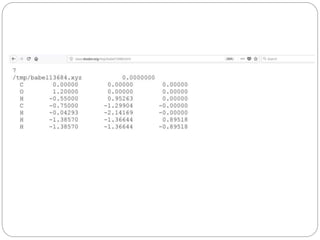
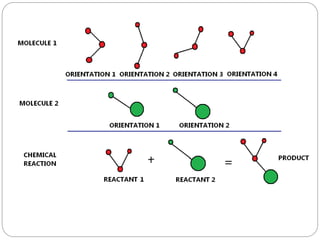
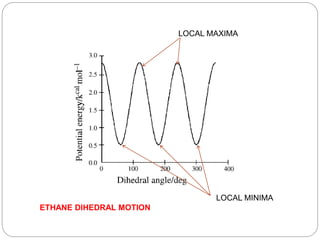
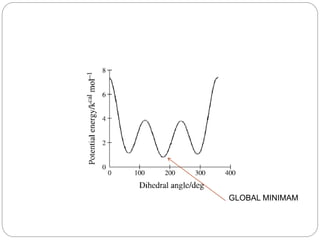
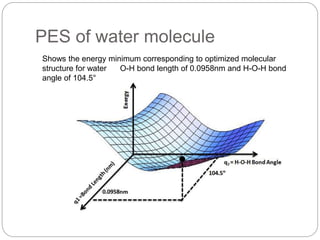
The document discusses Z-matrices and potential energy surfaces. It defines a Z-matrix as a way to represent molecules using internal coordinates like bond lengths, angles, and dihedrals. It then gives an example Z-matrix for methane. It also defines potential energy surfaces as describing the energy of a system, like a collection of atoms, in terms of parameters like atomic positions. It discusses how potential energy surfaces are used to theoretically explore molecular properties and chemical reactions.

1. PRESENTED BY:
VIJAY.S
MSFBI1521
Z MATRIX AND POTENTIAL
ENERGY SURFACE
BHARATHIDASAN UNIVERSITY
DEPARTMENT OF BIOINFORMATICS

2. Z MATRIX

3. INTRODUCTION
 The coordinate system is obviously important to b
able to specify the position of the atoms and
molecules in the system to a modelling program.
 There are two common ways to in which this can
be done.
1.cartesian coordinate
2.internal coordinate
 The most common straightforward approach is to
use specify the cartesian (x,y,z) coordinates of all
the atoms present.
 Internal coordinate in which the position of each
atom is described relative to other atoms in the
system. The internal coordinates is usually
written as a Z MATRIX.

4. Z MATRIX
 The Z-MATRIX is a way to represent a system
built of atoms.
 A Z-matrix is also known as an internal
coordinate
representation.
 It provides a description of each atom in a
molecule in terms of its atomic number, bond
length, bond angle, and dihedral angle, the so-
called internal coordinates.
 However, it is convenient to write a Z-matrix in
terms of bond lengths, angles, and dihedrals
since this will preserve the actual bonding

5.  The name arises because the Z-matrix assigns
the second atom along the Z axis from the first
atom, which is at the origin.
 Z-matrices can be converted to Cartesian
coordinates.
 They are used for creating input geometries for
molecular systems in many molecular modelling
and computational chemistry programs.

6. 1
2
3
6
5
7
8
4

7. A.N B.D A.C B.A A.C D.A D.C
1 C
2 C 1.54 1
3 H 1.0 1 109.5 2
4 H 1.0 2 109.5 1 180.0 3
5 H 1.0 1 109.5 2 60.0 4
6 H 1.0 2 109.5 1 -60.0 5
7 H 1.0 1 109.5 2 180.0 6
8 H 1.0 2 109.5 1 60.0 7
A.N-ATOM NAME
A.C-ATOM CONNECT
B.D-BOND DISTANCE
A.C-ANGLE CONNECT
B.A-BONDANGLE
D.A-DIGYDRAL ANGLE
D.C-DIHYDRAL
CONNECT

8. http://www.shodor.org/chemviz/zmatrices/babel.html

14. POTENTIAL ENERGY
SURFACE

15. INTRODUCTION
 A potential energy surface (PES) describes the
energy of a system, especially a collection of
atoms, in terms of certain parameters, normally
the positions of the atoms.
 The surface might define the energy as a function
of one or more coordinates.
 if there is only one coordinate, the surface is
called a potential energy curve or energy profile.

16.  The PES concept finds application in fields such
as chemistry and physics, especially in the
theoretical sub-branches of these subjects.
 It can be used to theoretically explore properties
of structures composed of atoms, for example,
finding the minimum energy shape of a molecule
or computing the rates of a chemical reaction.

17. BORN-OPPENHEIMER
APPROXIMATION
Ψ total = Ψ electronic x Ψ nuclear
 Computation of the energy and wave function
of a molecule.
 Born–Oppenheimer approximation allows the
wave function of a molecule to be broken into
its electronic and nuclear motions.
 Ψtotal = product function.

18. SCHRODINGER EQUATION
 Describes how the quantum state of a
physical system changes in time(time
independent)
H ψ= E ψ
 For a general quantum system(time
dependent)
 i imaginary unit
 Ψ(r,t) wave function
 ħ Planck constant
 Hamiltonian operator

20. A potential energy surface must be
created to take into account :
 1.Every possible orientation of the reactant
molecules
 2.Every possible orientation of the product
molecules
 3.The electronic energy of the reactant
molecules
 4.The electronic energy of the product
molecules

21. LOCAL MAXIMA
LOCAL MINIMA
ETHANE DIHEDRAL MOTION

22. GLOBAL MINIMAM

23. PES of water molecule
Shows the energy minimum corresponding to optimized molecular
structure for water O-H bond length of 0.0958nm and H-O-H bond
angle of 104.5°

24. ADVANTAGES :
The structure, energetics, properties, reactivity,
spectra and dynamics of molecules can be
readily understood in terms of potential energy
surfaces.
LIMITATIONS:
 Stability and reactivity are not precise
concepts
 Resonance, nucleophilicity, leaving group
ability not considered

25. REFERENCE
 Andrew Leach, Molecular Modelling: Principles
and Applications (2nd Edition), Addison Wesley
Longman, Essex, England, 1996

26. THANK YOU!!!