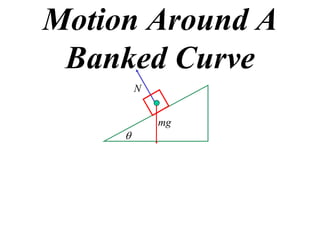
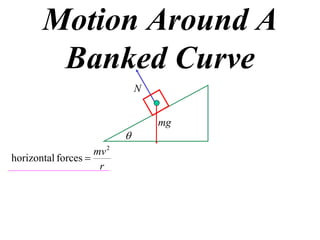
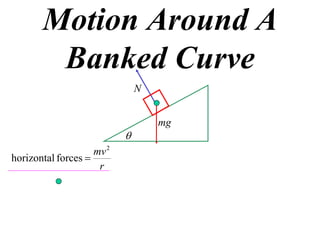
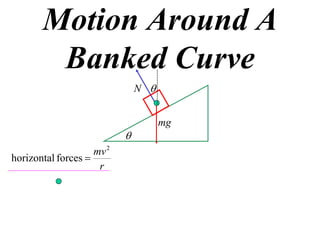
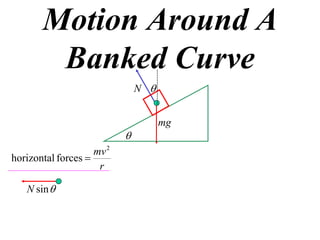
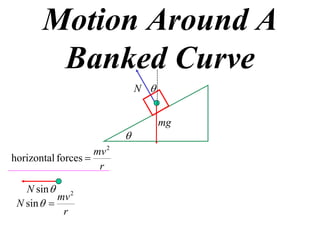
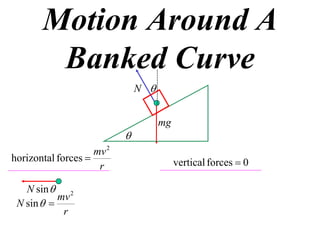
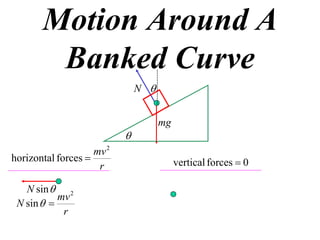
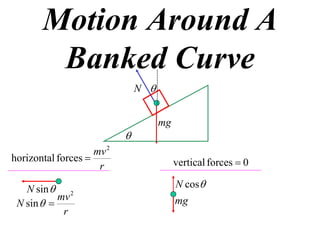
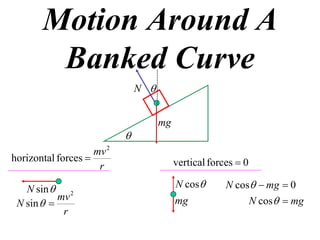
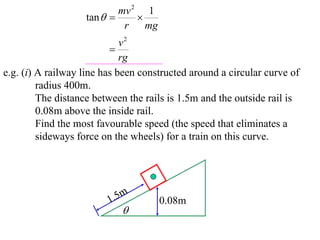
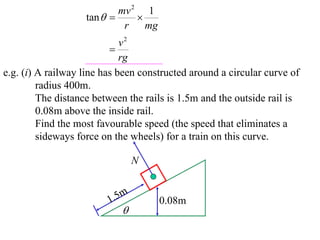
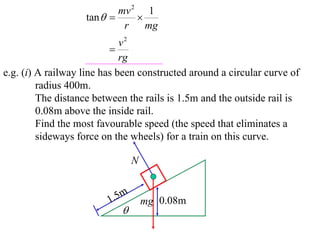
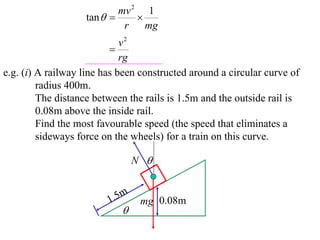
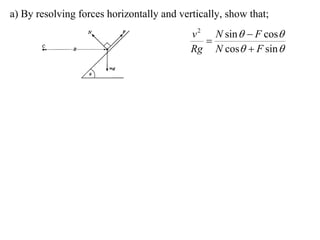
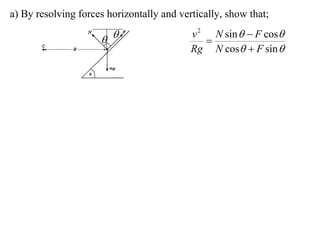
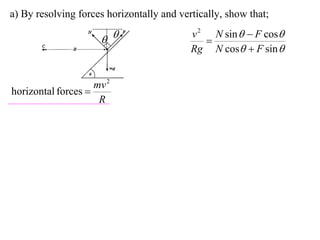
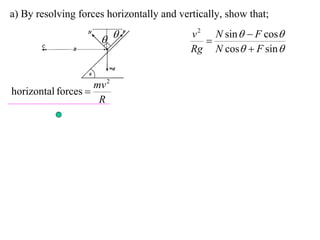
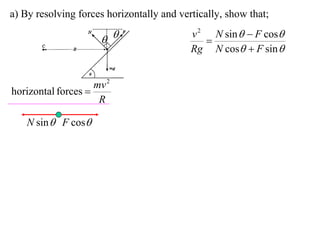
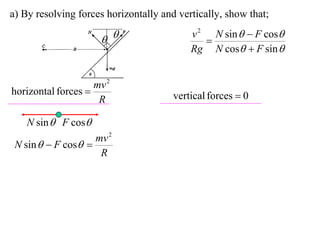
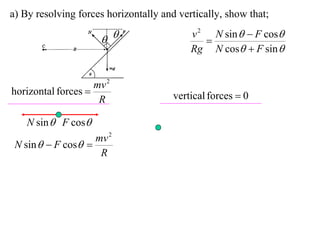
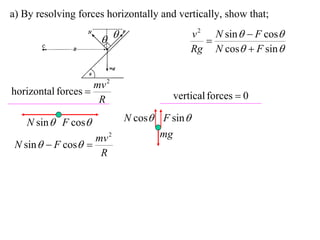
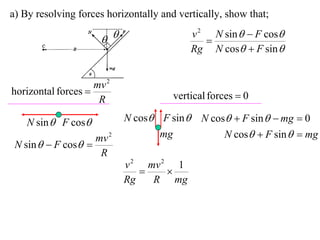
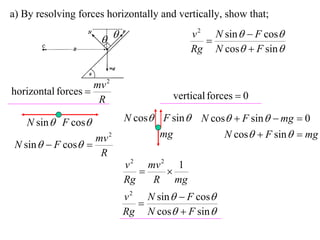
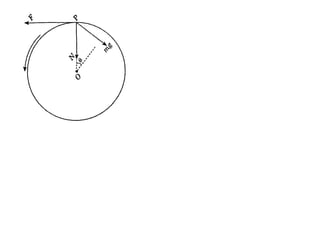
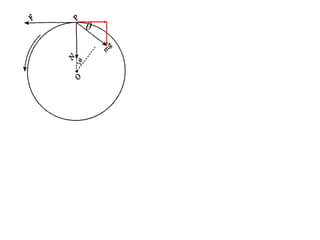
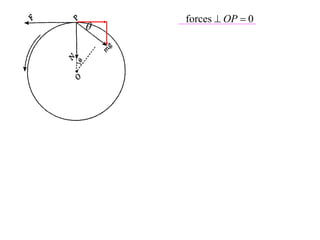
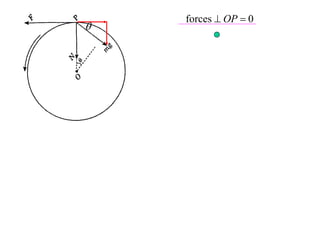
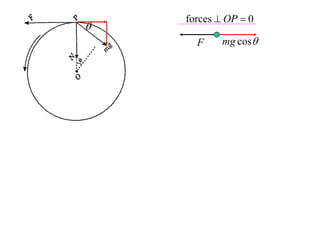
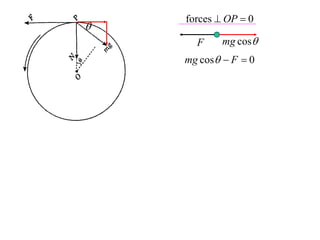
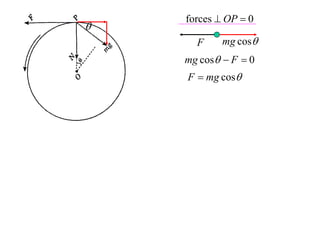
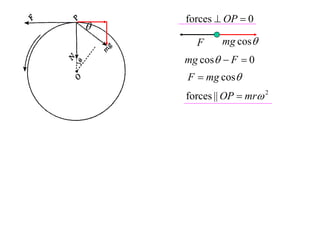
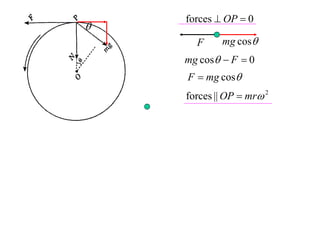
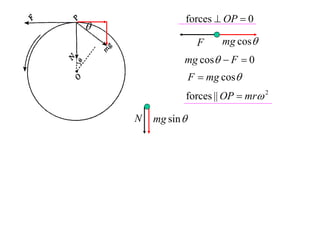
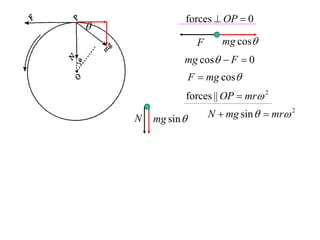
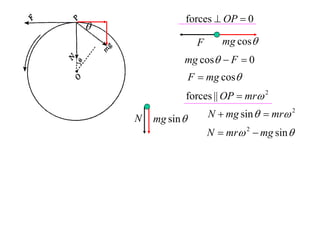
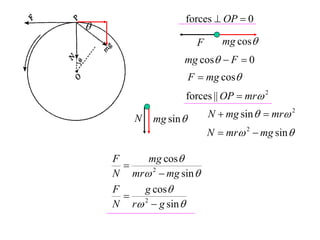
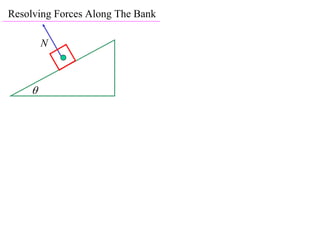
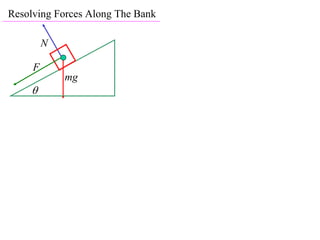
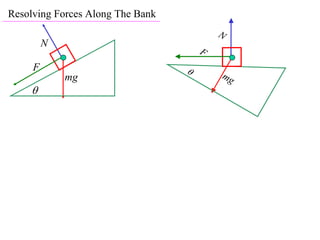
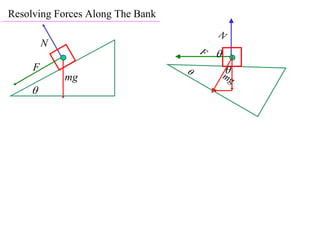
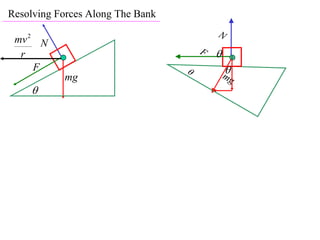
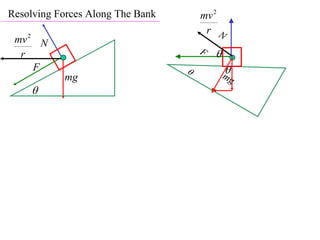
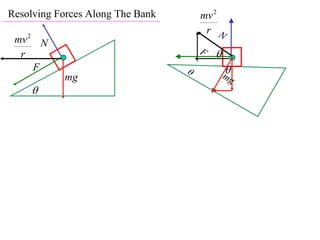
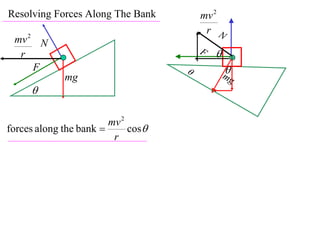
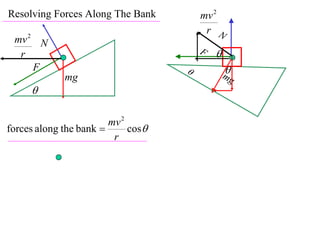
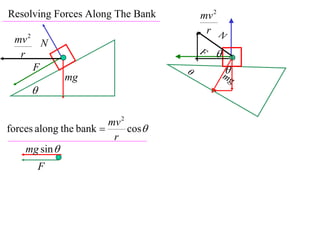
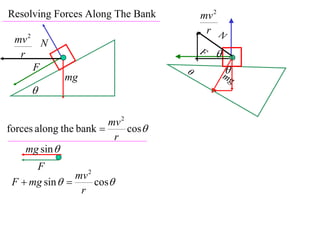
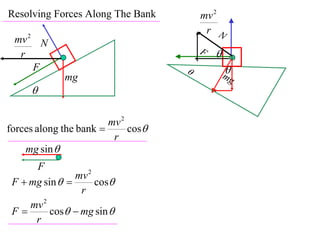
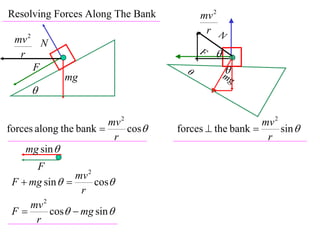
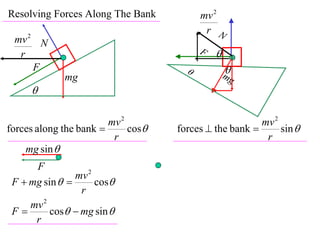
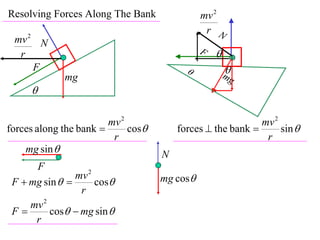
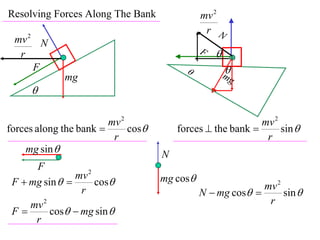
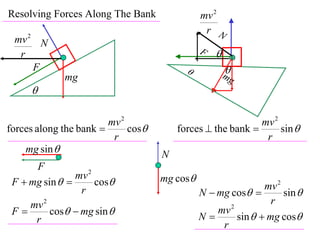
The document discusses motion around a banked curve. It defines the horizontal and vertical forces involved when an object moves around such a curve. It shows that for no sideways force, the horizontal centrifugal force must equal the horizontal component of the normal force from the bank. This allows deriving an equation that relates the angle of the bank, radius of the curve, and required speed to eliminate sideways forces. As an example, it calculates the most favorable speed for a train moving around a curved track with a given radius and bank angle.

1. Motion Around A
Banked Curve

2. Motion Around A
Banked Curve


3. Motion Around A
Banked Curve


4. Motion Around A
Banked Curve
N


5. Motion Around A
Banked Curve
N
mg


6. Motion Around A
Banked Curve
N
mg

mv 2
horizontal forces 
r

7. Motion Around A
Banked Curve
N
mg

mv 2
horizontal forces 
r

8. Motion Around A
Banked Curve
N 
mg

mv 2
horizontal forces 
r

9. Motion Around A
Banked Curve
N 
mg

mv 2
horizontal forces 
r
N sin 

10. Motion Around A
Banked Curve
N 
mg

mv 2
horizontal forces 
r
N sin  2
mv
N sin  
r

11. Motion Around A
Banked Curve
N 
mg

mv 2
horizontal forces  vertical forces  0
r
N sin  2
mv
N sin  
r

12. Motion Around A
Banked Curve
N 
mg

mv 2
horizontal forces  vertical forces  0
r
N sin  2
mv
N sin  
r

13. Motion Around A
Banked Curve
N 
mg

mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos
mv
N sin   mg
r

14. Motion Around A
Banked Curve
N 
mg

mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos N cos  mg  0
mv N cos  mg
N sin   mg
r

15. mv 2 1
tan   
r mg
v2

rg

16. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.

17. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.


18. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.
1 .5m


19. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.
1 .5m 0.08m


20. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.
1 .5m 0.08m


21. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.
N
1 .5m 0.08m


22. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.
N
1 .5m mg 0.08m


23. mv 2 1
tan   
r mg
v2

rg
e.g. (i) A railway line has been constructed around a circular curve of
radius 400m.
The distance between the rails is 1.5m and the outside rail is
0.08m above the inside rail.
Find the most favourable speed (the speed that eliminates a
sideways force on the wheels) for a train on this curve.
N 
1 .5m mg 0.08m


24. mv 2
horizontal forces 
r

25. mv 2
horizontal forces 
r

26. mv 2
horizontal forces 
r
N sin 

27. mv 2
horizontal forces 
r
N sin  2
mv
N sin  
r

28. mv 2
horizontal forces  vertical forces  0
r
N sin  2
mv
N sin  
r

29. mv 2
horizontal forces  vertical forces  0
r
N sin  2
mv
N sin  
r

30. mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos
mv
N sin   mg
r

31. mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos N cos  mg  0
mv N cos  mg
N sin   mg
r

32. mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos N cos  mg  0
mv N cos  mg
N sin   mg
r
mv 2 1
tan   
r mg
v2

rg

33. mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos N cos  mg  0
mv N cos  mg
N sin   mg
r
mv 2 1
tan   
r mg
v2

rg
0.08
But sin  
1.5
4

75

34. mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos N cos  mg  0
mv N cos  mg
N sin   mg
r
mv 2 1
tan   
r mg
v2

rg
0.08
But sin  
1.5
4

75
4
 tan  
5609

35. mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos N cos  mg  0
mv N cos  mg
N sin   mg
r
mv 2 1 v2 4
tan     
r mg 4009.8 5609
v2

rg
0.08
But sin  
1.5
4

75
4
 tan  
5609

36. mv 2
horizontal forces  vertical forces  0
r
N sin  2 N cos N cos  mg  0
mv N cos  mg
N sin   mg
r
mv 2 1 v2 4
tan     
r mg 4009.8 5609

v2 4400 9.8
rg v2 
5609
0.08
But sin   v  14.47 m/s
1.5 v  52km/h
4

75
4
 tan  
5609

37. (ii) (1995)
A particle of mass m travels at a constant speed v round a circular
track of radius R, centre C. The track is banked inwards at an angle  ,
and the particle does not move up or down the bank.
The reaction exerted by the track on the particle
has a normal component N, and a component F
due to friction, directed up or down the bank.
The force F lies in the range  N to N ,
where  is a positive constant and N is the
normal component; the sign of F is positive
when F is directed up the bank.
The acceleration due to gravity is2 g. The acceleration related to the
circular motion is of magnitude v and is directed towards the centre
of the track. R

38. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos

Rg N cos  F sin 

39. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 

40. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces 
R

41. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces 
R

42. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces 
R
N sin  F cos

43. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces 
R
N sin  F cos
mv 2
N sin   F cos 
R

44. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces  vertical forces  0
R
N sin  F cos
mv 2
N sin   F cos 
R

45. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces  vertical forces  0
R
N sin  F cos
mv 2
N sin   F cos 
R

46. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces  vertical forces  0
R
N sin  F cos N cos F sin 
mv 2 mg
N sin   F cos 
R

47. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces  vertical forces  0
R
N sin  F cos N cos F sin  N cos  F sin   mg  0
mv 2 mg N cos  F sin   mg
N sin   F cos 
R

48. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces  vertical forces  0
R
N sin  F cos N cos F sin  N cos  F sin   mg  0
mv 2 mg N cos  F sin   mg
N sin   F cos 
R
v 2 mv 2 1
 
Rg R mg

49. a) By resolving forces horizontally and vertically, show that;
v 2 N sin   F cos
  
Rg N cos  F sin 
mv 2
horizontal forces  vertical forces  0
R
N sin  F cos N cos F sin  N cos  F sin   mg  0
mv 2 mg N cos  F sin   mg
N sin   F cos 
R
v 2 mv 2 1
 
Rg R mg
v 2 N sin   F cos

Rg N cos  F sin 

50. b) Show that the maximum speed vmaxat which the particle can travel
without slipping up the track is given by; vmax tan   
2

Rg 1   tan 
You may suppose that  tan   1

51. b) Show that the maximum speed vmaxat which the particle can travel
without slipping up the track is given by; vmax tan   
2

Rg 1   tan 
You may suppose that  tan   1
As it is the friction that resists the particle moving up or down the slope,
then if the particle is not slipping up, then friction must be at a maximum
in the opposite direction, i.e. F   N

52. b) Show that the maximum speed vmaxat which the particle can travel
without slipping up the track is given by; vmax tan   
2

Rg 1   tan 
You may suppose that  tan   1
As it is the friction that resists the particle moving up or down the slope,
then if the particle is not slipping up, then friction must be at a maximum
in the opposite direction, i.e. F   N
vmax N sin   N cos
2

Rg N cos  N sin 

53. b) Show that the maximum speed vmaxat which the particle can travel
without slipping up the track is given by; vmax tan   
2

Rg 1   tan 
You may suppose that  tan   1
As it is the friction that resists the particle moving up or down the slope,
then if the particle is not slipping up, then friction must be at a maximum
in the opposite direction, i.e. F   N
vmax N sin   N cos
2

Rg N cos  N sin 
sin  cos

 cos cos
cos sin 

cos cos
tan   

1   tan 

54. c) Show that if   tan  , then the particle will not slide down the track,
regardless of its speed.

55. c) Show that if   tan  , then the particle will not slide down the track,
regardless of its speed.
vmin is the minimum speed the particle can travel without sliding down
the track. In this case friction must be a maximum up the slope
i.e. F  N

56. c) Show that if   tan  , then the particle will not slide down the track,
regardless of its speed.
vmin is the minimum speed the particle can travel without sliding down
the track. In this case friction must be a maximum up the slope
i.e. F  N
vmin tan   
2

Rg 1   tan 

57. c) Show that if   tan  , then the particle will not slide down the track,
regardless of its speed.
vmin is the minimum speed the particle can travel without sliding down
the track. In this case friction must be a maximum up the slope
i.e. F  N
vmin tan   
2

Rg 1   tan 
If   tan  ;

58. c) Show that if   tan  , then the particle will not slide down the track,
regardless of its speed.
vmin is the minimum speed the particle can travel without sliding down
the track. In this case friction must be a maximum up the slope
i.e. F  N
vmin tan   
2

Rg 1   tan 
If   tan  ; 2
vmin
 0
Rg

59. c) Show that if   tan  , then the particle will not slide down the track,
regardless of its speed.
vmin is the minimum speed the particle can travel without sliding down
the track. In this case friction must be a maximum up the slope
i.e. F  N
vmin tan   
2

Rg 1   tan 
If   tan  ; 2
vmin
 0
Rg
vmin  0
2
vmin  0

60. c) Show that if   tan  , then the particle will not slide down the track,
regardless of its speed.
vmin is the minimum speed the particle can travel without sliding down
the track. In this case friction must be a maximum up the slope
i.e. F  N
vmin tan   
2

Rg 1   tan 
If   tan  ; 2
vmin
 0
Rg
vmin  0
2
vmin  0
Thus if the minimum velocity the particle can travel without sliding
down the track is 0, the particle will not slide down the track, regardless
of its speed.

61. (iii) (1996)
A circular drum is rotating with uniform angular velocity round a
horizontal axis. A particle P is rotating in a vertical circle, without
slipping, on the inside of the drum.
The radius of the drum is r metres and its angular velocity is 
radians/second. Acceleration due to gravity is g metres/second 2, and
the mass of P is m kilograms.
The centre of the drum is O, and OP makes an
angle of  to the horizontal.
The drum exerts a normal force N on P, as well
as frictional force F, acting tangentially to the
drum, as shown in the diagram.
By resolving forces perpendicular to and
parallel to OP, find an expression for F in
terms of the data. N

63. 

64. forces  OP  0


65. forces  OP  0


66. forces  OP  0

F mg cos

67. forces  OP  0

F mg cos
mg cos  F  0

68. forces  OP  0

F mg cos
mg cos  F  0
F  mg cos

69. forces  OP  0

F mg cos
mg cos  F  0
F  mg cos
forces || OP  mr 2

70. forces  OP  0

F mg cos
mg cos  F  0
F  mg cos
forces || OP  mr 2

71. forces  OP  0

F mg cos
mg cos  F  0
F  mg cos
forces || OP  mr 2
N mg sin 

72. forces  OP  0

F mg cos
mg cos  F  0
F  mg cos
forces || OP  mr 2
N mg sin  N  mg sin   mr 2

73. forces  OP  0

F mg cos
mg cos  F  0
F  mg cos
forces || OP  mr 2
N mg sin  N  mg sin   mr 2
N  mr 2  mg sin 

74. forces  OP  0

F mg cos
mg cos  F  0
F  mg cos
forces || OP  mr 2
N mg sin  N  mg sin   mr 2
N  mr 2  mg sin 
F mg cos

N mr 2  mg sin 
F g cos
 2
N r  g sin 

75. Resolving Forces Along The Bank

76. Resolving Forces Along The Bank


77. Resolving Forces Along The Bank


78. Resolving Forces Along The Bank
N


79. Resolving Forces Along The Bank
N
mg


80. Resolving Forces Along The Bank
N
F
mg


81. Resolving Forces Along The Bank
N
N
F
F 
mg mg


82. Resolving Forces Along The Bank
N
N
F 
F  
mg
mg


83. Resolving Forces Along The Bank
N
mv 2 N
r F 
F  
mg
mg


84. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg


85. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg


86. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2
forces along the bank  cos
r

87. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2
forces along the bank  cos
r

88. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2
forces along the bank  cos
r
mg sin 
F

89. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2
forces along the bank  cos
r
mg sin 
F
mv 2
F  mg sin   cos
r

90. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2
forces along the bank  cos
r
mg sin 
F
mv 2
F  mg sin   cos
r
mv 2
F cos  mg sin 
r

91. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2 mv 2
forces along the bank  cos forces  the bank  sin 
r r
mg sin 
F
mv 2
F  mg sin   cos
r
mv 2
F cos  mg sin 
r

92. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2 mv 2
forces along the bank  cos forces  the bank  sin 
r r
mg sin 
F
mv 2
F  mg sin   cos
r
mv 2
F cos  mg sin 
r

93. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2 mv 2
forces along the bank  cos forces  the bank  sin 
r r
mg sin  N
F
mv 2 mg cos
F  mg sin   cos
r
mv 2
F cos  mg sin 
r

94. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2 mv 2
forces along the bank  cos forces  the bank  sin 
r r
mg sin  N
F
mv 2 mg cos
F  mg sin   cos mv 2
r N  mg cos  sin 
mv 2 r
F cos  mg sin 
r

95. Resolving Forces Along The Bank mv 2
r N
mv 2 N
r F 
F  
mg
mg

mv 2 mv 2
forces along the bank  cos forces  the bank  sin 
r r
mg sin  N
F
mv 2 mg cos
F  mg sin   cos mv 2
r N  mg cos  sin 
mv 2 r
F cos  mg sin 
2
mv
r N sin   mg cos
r

96. Exercise 9D; all