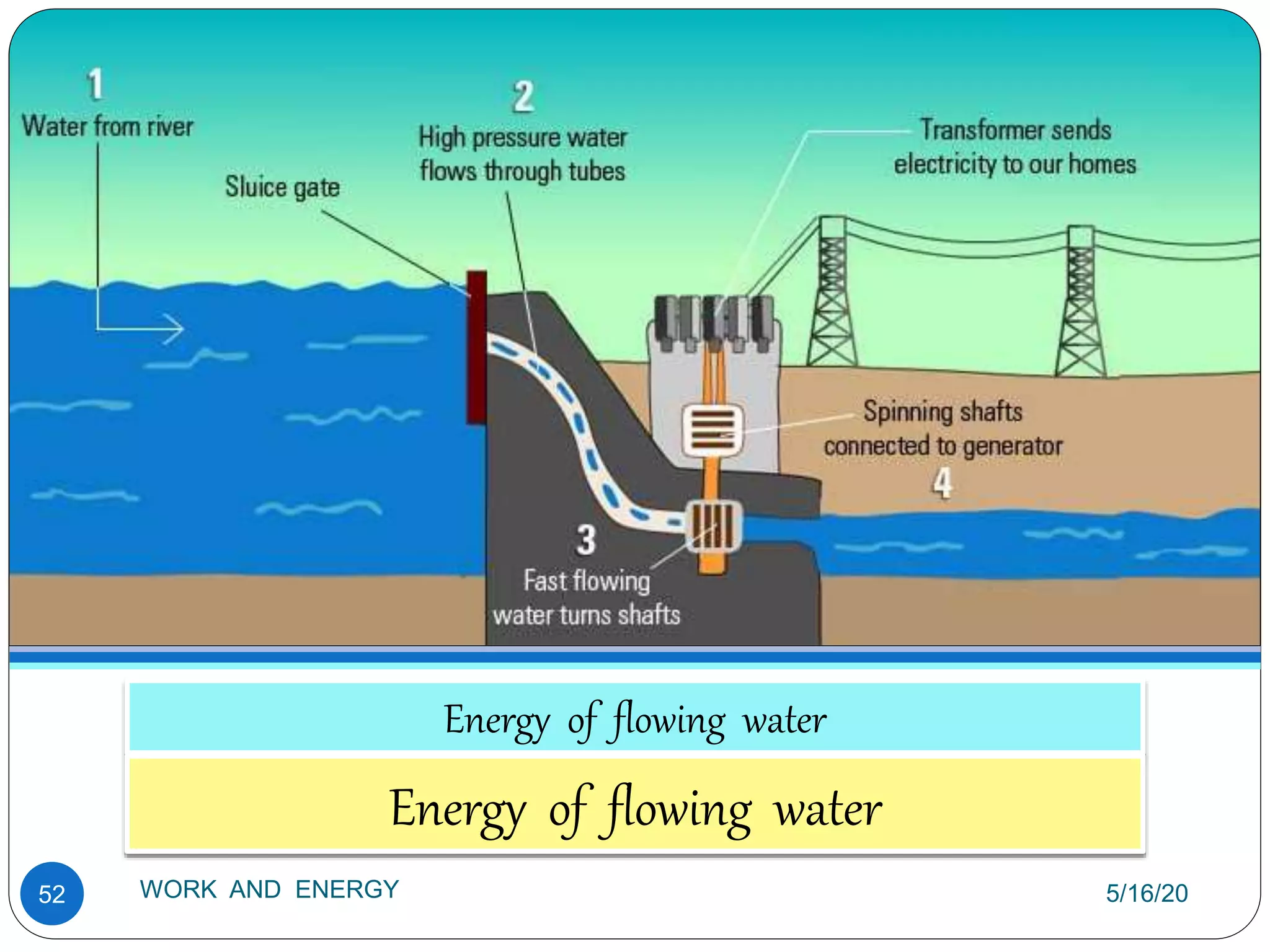
This document provides information about work and energy covered in class 9th C. It discusses various topics like concept of work, factors on which amount of work depends, positive and negative work, zero work, different forms of energy, mechanical energy, kinetic energy and potential energy. Examples are given to explain these concepts in detail. The document also provides units of work, power and energy.

1. •Name:- Ojaswa Maurya
•Class :- 9th C
•Roll no:- 33
•School:- Kendriya Vidyalya Ambernath
Work and energy

2. Topics covered in this chapter
 Concept of Work
 Factors on Which Amount of Work Done
Depends.
 Work Done by a Constant Force.
 Unit of Work.
 Work Done Against Gravitational Force.
 Nature of Work
 Positive Work .
 Negative Work .
 Zero Work .
5/16/20
2 WORK AND ENERGY

3. Forms of Energy
•Transformation of Energy
 Transformation of Energy in Nature
•Law of Conservation of Energy
 Verification of law of Conservation of Energy
•Rate of Doing Work : Power
 Power in Terms of Energy
Average Power
Units of Power
Commercial Unit of Energy
•ENERGY
5/16/20
3 WORK AND ENERGY

4. 5/16/20
4 WORK AND ENERGY
Note :- In layman language the word “Work”
means any physical or mental activity that
we do in our daily life.

5. What is work ?
5/16/20
WORK AND ENERGY
5
ANS:- Work is a physical quantity in which
some conditions are needed to be satisfied
for it to be done. To understand it’s concept
let’s take a example. :- A book on table when
you push it , it move change it’s state and
direction.

6. FACTORS ON WHICH AMOUNT OF WORK DEPENDS
5/16/20
WORK AND ENERGY
6
1. Magnitude of force applied on a body.
W is directly proportion to F
2. Displacement of body.
W is directly proportion to s
3. Work done is also depends angle of
between force and displacement.
W is directly proportion to
FSCOSt
Note:- W = work s=
displacement
F = force t= theta

7. Work done by constant force
5/16/20
WORK AND ENERGY
7
 A constant force F acting on a body produces
displacement s in the direction of the force, work
done W by this, force is equal to the product force
and the displacement.
W = Fs
As displacement is in direction of the applied force
=> t = 0°=> COS0°=1

8. 5/16/20
WORK AND ENERGY
8
• A constant retarding force F acting on a body
moving with a uniform velocity along a particular
direction. The body will stop after covering certain
displacement s. In this situation the applied force is
opposing the motion of the body , applied force F is
taken as negative.
W=(-Fs)
Negative sign represent that the work is done by
retarding force
CONCLUSION:- “Work is said to be done by a
force when a force is applied on a body and body
gets displaced due to the action of applied force.”

9. UNIT OF WORK
5/16/20
WORK AND ENERGY
9
 The SI unit of force is Newton (N) and that of
displacement is meter (m). So the SI unit of work
is Newton meter which is written as Nm. This unit
is called joule (J) In the honor of a British
scientist, James Prescott Joule.
If F=1N,s=1m
then W=1N*1m=1Nm
Thus, 1 joule is the amount of work done on an
object when force of 1N displaces it by 1m in the
direction of force applied .
1J=1Nm

10. Work done against gravitational force
5/16/20
WORK AND ENERGY
10
 If we lift a bucket from ground, we do work
against gravitational force. When a body is lifted
vertically upwards the force required to lift the
body is equal to it’s weight. Thus, “whenever work
is done against gravity, then amount of work done
is equal to product of the weight of the body and
vertical distance through which the body is lifted”.

11. 5/16/20
WORK AND ENERGY
11
Let a body of mass m be lifted vertically
upwards through a height h. Here the force
required to lift the body will be equal to weight of
the body (mg), where g is acceleration due to
gravity.
Then work done in lifting of the body
W= weight of the body * vertical distance
W=(mg)(h)

12. 5/16/20
WORK AND ENERGY
12

13. POSITVE WORK
5/16/20
WORK AND ENERGY
13
Work done is said to be positive if the force
applied on an object and it’s displacement are in
the same direction or angel or angel between the
force and displacement of the object is less than
90 degree (theta < 90 degree).
Illustration 1:- when a lawn mower is pushed by
applying force along the handle at an acute angle,
work done by the applied force is positive as
shown in the figure.

14. 5/16/20
WORK AND ENERGY
14
Illustration 2:- When a body falls under the
action of gravity, angle between the force
and displacement is zero, t=0. therefore the
work done by the body is positive.
s

15. Negative work
5/16/20
WORK AND ENERGY
15
 Work done is said to be negative if the applied
force on an object and it’s direction of motion is
opposite or component for the applied force and
direction of motion should be obtuse (theta > 90
degree).
Example:- A bucket is pulled upward by a force F
and it moves some distance s vertically upward.
But the force of gravity always acts in the
downward direction. Then work done by the
gravity is given by.
W=( -Fs)

16. 5/16/20
WORK AND ENERGY
16
Illustration 1:-When a body is displaced by
distance d vertically upwards, its motion is
opposed by the gravity. In this case angel
between weight and displacement
theta=180 degree.
Work done by gravity
The motion is opposed by gravity, In this
case angel between weight and
displacement, theta=180 degree because
the gravitational force displacement are in
opposite direction.
W=(-Fs )
Thus, work done is negative.

17. 5/16/20
WORK AND ENERGY
17
Work done by applied force
In this case, angel between applied
force and displacement, theta=0 degree,
because the applied force and
displacement are in same direction.
W=Fs
Thus, work done by the applied force is
positive
Work done by the gravity is negative
while work done by the applied force is
positive.

18. ZERO WORK
5/16/20
WORK AND ENERGY
18
 Work done will be 0 if
a. Force acting is zero
b. Displacement is 0
c. Angel between applied force on an object and
it’s displacement is 90 degree
Illustration1:- When a body is tied to one end of a
string and is moved in a circular path, work
done by the centripetal force is zero. Because,
force is always perpendicular to the
displacement of the body.

19. 5/16/20
WORK AND ENERGY
19
Illustration 2:- Work done by tension in the string
of a simple pendulum is zero. Because, tension
is always perpendicular to the displacement of
the bob.

20. 5/16/20
WORK AND ENERGY
20

21. What is energy ?
5/16/20
WORK AND ENERGY
21
 Energy of a body is defined as the capacity or
ability of the body to do work. The amount of
energy possessed by a body is equal to the
amount of work it can do when its energy is
released.
Note:- More the amount of energy possessed by a body,
more the amount of work it can do an vice versa.
Energy is a scalar quantity. It has only magnitude
but no direction.

22. 5/16/20
WORK AND ENERGY
22

23. Unit of energy
5/16/20
WORK AND ENERGY
23
 As we know that, energy possessed by a body is
measured in terms of ability of the body to do
work. Therefore, the S.I unit of energy is the
same as the unit of work i.e. joule.
1 joule is the energy required to do 1 joule
of work.
larger unit is KJ
1KJ=1000 J
Smaller unit of energy is eV ( electron volt)
1eV=1.6*10^(-9) J
CGS unit of energy is
1J=10^7 erg

24. FORMS OF ENERGY
5/16/20
WORK AND ENERGY
24
ENERGY
HEAT
ENERG
Y
NIL
NIL
LIGHT
ENERG
Y
NIL

25. 5/16/20
WORK AND ENERGY
25
HEAT ENERGY:- Heat can be defined as
the form of energy that is transferred
between two points .
EXAMPLE:-
• Steam of water
• Car engine
LIGHT ENERGY:- Light is also form of
energy to prove that let’s take example plant
make their own food with the help of light
energy or when light energy falls on
photographic plate it cause a chemical
reaction and hence image are recorded in

26. 5/16/20
WORK AND ENERGY
26
ENERGY
2
Electrical
Energy
NIL
NIL
Chemical
Energy NIL

27. 5/16/20
WORK AND ENERGY
27
ELECTRICAL ENERGY:- Electrical energy is a
form of energy resulting from the flow
of electric charge. Energy is the ability to do work
or apply force to move an object. In the case
of electrical energy, the force
is electrical attraction or repulsion between
charged particles.
CHEMICAL ENERGY:- Chemical
energy is energy stored in the bonds
of chemical compounds, like atoms and
molecules. This energy is released when
a chemical reaction takes place. Usually,
once chemical energy has been released from a

28. 5/16/20
WORK AND ENERGY
28
ENERG
Y 3
SOUND
ENERGY
NIL
NIL
Magnetic
Energy NIL

29. 5/16/20
WORK AND ENERGY
29
• SOUND ENERGY:- In physics, sound energy
is a form of energy that can be heard by
humans. Sound is a mechanical wave and as
such consists physically in oscillatory elastic
compression and in oscillatory displacement of
a fluid. Therefore, the medium acts as storage
for both potential and kinetic energy.
• MEGNETIC ENERGY:- Magnetic energy and
electrostatic potential energy are related by
Maxwell's equations. The potential energy of a
magnet of magnetic moment in a magnetic
field is defined as the mechanical work of the

30. 5/16/20
WORK AND ENERGY
30
ENERGY
4
Mechani
cal
Energy
Kinetic
energy
Potential
energy
Nuclear NIL

31. 5/16/20
WORK AND ENERGY
31
NUCLEAR ENERGY:- Nuclear power
is the use of nuclear reactions
that release nuclear energy to
generate heat, which most
frequently is then used in steam
turbines to produce electricity in
a nuclear power plant. Nuclear
power can be obtained from
nuclear fission, nuclear decay
and nuclear fusion reactions.

32. What is mechanical energy
5/16/20
WORK AND ENERGY
32
In physical sciences, mechanical energy
is the sum of potential energy and
kinetic energy. It is the macroscopic
energy associated with a system. The
principle of conservation of mechanical
energy states that in an isolated system
that is only subject to conservative
forces, the mechanical energy is
constant. There are two types of
mechanical energy KINETIC ENERGY
and POTENTIAL ENERGY.

33. MECHANICAL ENERGY
KINETIC ENERGY POTENTIAL ENERGY
5/16/20
WORK AND ENERGY
33
The energy
possessed by the
body by the virtue of
it’s motion is called
kinetic energy. An
object in motion
has the ability to do
work and hence
possesses kinetic
energy.
In physics, potential
energy is
the energy held by
an object because of
its position relative
to other objects,
stresses within
itself, its electric
charge, or other
factors.

34. KINETIC ENERGY
5/16/20
WORK AND ENERGY
34
 Expression for kinetic energy(work-
energy theorem)
Question 1):- Consider an object of mass m moving
with a uniform velocity, u. let it now be displaced
through a distance s, when a constant force ,F,
act on it. The work done on the object will cause a
change in it’s velocity change from u to v. Let ‘a’
be the acceleration produced.
v^2 = u^2 + 2as
s = (v^2 - u^2) / 2a …….(i)

35. 5/16/20
WORK AND ENERGY
35
According to Newton's second law of motion the
force applied on an body is
F=ma ……(ii)
The work done by the force is
W = force * displacement
= ma * (v^2 – u^2) / 2a
W = ½*m(v^2 – u^2)= ½*mv^2 –
½*mu^2=change in KE
The energy spent in doing this work of moving body
from rest (u=0) to attain a uniform velocity v is
stored in the body in the form of kinetic energy.

36. 5/16/20
WORK AND ENERGY
36
Therefore, work done = change in kinetic energy.
This is the work-energy theorem
So, K.E.=(1/2)*mv^2 …....(iii) [ when u= 0]

37. Potential energy
5/16/20
WORK AND ENERGY
37
The energy possessed by a body by the
virtue of it’s position or it’s configuration
is called potential energy. An object may
have the capacity of doing work as a
result of it’s position in a gravitational
field, an electric field or a magnetic field.
Potential energy may be positive or
negative. Potential energy is often
referred by stored energy. There are two
types of potential energy elastic
potential energy and gravitational
potential energy.

38. 5/16/20
WORK AND ENERGY
38

39. ELASTIC POTENTIAL ENERGY
5/16/20
WORK AND ENERGY
39
 Elastic energy is the mechanical
potential energy stored in the
configuration of a material or
physical system as it is
subjected to elastic deformation
by work performed upon it.
Elastic energy occurs when
objects are impermanently
compressed, stretched or

40. 5/16/20
WORK AND ENERGY
40
Some examples of elastic
potential energy.
•The coil spring of a wind-up clock.
•An archer's stretched bow.
•A bent diving board, just before a
divers jump.
•The twisted rubber band which
powers a toy airplane.
•A bouncy ball, compressed at the
moment it bounces off a brick wall.

41. GRAVITATIONAL POTENTIAL ENERGY
5/16/20
WORK AND ENERGY
41
In classical mechanics, the
gravitational potential at a
location is equal to the work
per unit mass that would be
needed to move an object to
that location from a fixed
reference location. It is
analogous to the electric
potential with mass playing
the role of charge

42. 5/16/20
WORK AND ENERGY
42
 Some examples of gravitational
potential energy
(a) The work done to lift the
weight is stored in the mass-
Earth system as gravitational
potential energy.
(b) As the weight moves
downward, this gravitational
potential energy is transferred

43. 5/16/20
WORK AND ENERGY
43

44. 5/16/20
WORK AND ENERGY
44

45. 5/16/20
WORK AND ENERGY
45
The change in one form of energy into
other is known as transformation of energy.
Examples:- When a piece of stone is thrown
upward. It’s kinetic energy start decreasing
and potential energy start increasing and when
the stone reaches at the maximum height of
it’s path, it’s kinetic becomes zero and it’s
potential energy becomes maximum. Thus at
the highest point, the total energy of the stone
will be only potential energy. So it can be
concluded that, “ when a body is thrown
upwards the kinetic energy of a body is
changed into potential energy.

46. 5/16/20
WORK AND ENERGY
46

47. TRANSFORMATION OF ENERGY IN NATURE
5/16/20
WORK AND ENERGY
47
1. ENERGY OF WIND:- The sun heat causes
uneven heating of land and produces
different air pressure at different places.
These differences in air pressure produces
wind, having kinetic energy. Wind energy is
used to run wind mill.
2. ENERGY OF FOOD:- The plants use the
sun energy to prepare food by the process
of photosynthesis. This energy gets stored in
food in the form of chemical energy. Humans
and animals eat these as food. This food
supplies energy to us. Muscular energy is
used by us to do work.

48. ENERGY OF WIND
ENERGY OF WIND
5/16/20
WORK AND ENERGY
48

49. ENERGY OF FOOD
ENERGY OF FOOD
5/16/20
WORK AND ENERGY
49

50. 5/16/20
WORK AND ENERGY
50
3. ENERGY OF FOSSIL FUEL:- The dead plants
and animals buried under earth millions of years
ago have been converted into fossil fuel like coal,
petroleum, oil and natural gas. The energy of
fossil fuel have can be used to produce thermal
energy, electrical energy and mechanical energy.
4. ENERGY OF FLOWING WATER:- The sun’s heat
energy causes water to evaporate from lakes,
rivers and oceans. The water vapours rise in the
air to form clouds. When this water falls back to
the earth in form of rain some amounts of this
stored in dam, it’s potential energy is converted
into kinetic energy which can be used to turn
turbine in the dams to generate electricity.

51. ENERGY OF FOSSIL FUEL
ENERGY OF FOSSIL FUEL
5/16/20
WORK AND ENERGY
51

52. Energy of flowing water
Energy of flowing water
5/16/20
WORK AND ENERGY
52

53. 5/16/20
WORK AND ENERGY
53

54. 5/16/20
WORK AND ENERGY
54
According to the law of
conservation of energy,
energy neither be created
nor be destroyed. It can only
change from on to another
form. The total energy after
conversation will be same. It
is valid in all situation and

55. Verification of law of conservation of energy
5/16/20
WORK AND ENERGY
55
 Consider a body of mass m, allowed to fall
freely from a height h.
GROUND
h
x
( h-x)
A
B
C

56. 5/16/20
WORK AND ENERGY
56
At position A
Kinetic energy of body (K.E.)= 0,
Because velocity is 0
Potential energy of body at A, is
P.E.= mgh
Total mechanical energy at A is (E1)
E1 = (K.E.)+(P.E.)
= 0 + mgh
E1=mgh
As it falls, it’s potential energy decreases and kinetic
energy increases. Let the body at B have velocity V1
where AB=x.

57. 5/16/20
WORK AND ENERGY
57
v1^2=u^2 + 2as
v1^2=0+2gx
v1^2=2gx
At position B
Kinetic energy=(1/2)*mv1^2=(1/2)m*2gx=mgx
Potential energy=mg(h-x)
Total mechanical energy at B is (E2)
E2= K.E.+P.E.
= mgx+mg(h-x)
E2=mgh
When the body is about to reach the ground at C
with velocity v.

58. 5/16/20
WORK AND ENERGY
58
At position C
Kinetic energy of the body (K.E.)=(1/2)mv^2
V^2=0+2gh=2gh
K.E.=mgh
Potential energy of the body at C
P.E.=mg(0)=0
Total mechanical energy E3
E3=K.E.+P.E.=mgh+0=mgh
E3=mgh
Thus, we find that
E1=E2=E3=mgh
Total mechanical energy always remain constant at
each point of motion of a body falling freely under
gravity, this verifies the law of conservation of energy.

59. 5/16/20
WORK AND ENERGY
59
CONCLUSION:-
As the body falls it’s potential energy decreases and
kinetic energy increases. The potential energy gets
converted into kinetic energy.
AT A:- The energy of the body is entirely potential
AT B:- The energy is partly kinetic and partly
potential. But total mechanical energy remains
constant.
AT C:- The energy is entirely kinetic, potential energy
is zero but total mechanical energy remains constant.
i.e.… K.E.+P.E.=Constant.

60. 5/16/20
WORK AND ENERGY
60

61. 5/16/20
WORK AND ENERGY
61
The definition of work say nothing
about how long it takes to do the work.
The same amount of work is done
when carrying up a load on stairs,
whether we walk up or ran up. So, why
we tired more after running up stairs in
a few second than after walking
upstairs in a few minutes? To
understand this difference we need to
talk about a measure of how fast the
work is done- power. Power is equal to
the amount of work done per unit time

62. 5/16/20
WORK AND ENERGY
62
Let two persons A and B of equal
weight, both start climbing up a rope
separately and reach at the height of
8 m. Let A takes 30 seconds while B
takes 20 seconds to accomplish the
task. Their work is same however A
has taken much time than B to do the
same work. i.e., The rate of doing
work by A is smaller than that of B.
Rate of doing work is power.

63. 5/16/20
WORK AND ENERGY
63
i.e., Power= Work done / Time taken
Or, P=W/T
Thus, power depends upon two factors, viz. On the
amount of work done and time taken.
i. When a body takes lesser time to do a particular
amount of work, it’s power is said to be greater
because Power is directly
proportion to (1/time) and vice-versa
ii. When a body does more amount of work in a
given time, it’s power said to be greater and vice-
versa, because Power is directly
proportion to Work.

64. Power in terms of energy
5/16/20
WORK AND ENERGY
64
As we know that energy is the ability of a body
to do work and power is the rate of doing
work. Thus, for doing particular work, an equal
amount of energy is required
Therefore,
Work done = Energy transferred
=> Power =(Energy transferred/Time
taken)= E/T
So, the rate of energy transferred by a body is
also called it’s power.

65. Average power
5/16/20
WORK AND ENERGY
65
Average power= Total amount of
work done/ Total time taken
= Total energy
supplied/ Total time taken
Power is a scalar quantity. It has
only magnitude but no direction.

66. Units of power
5/16/20
WORK AND ENERGY
66
Work is measured in ‘joule’ and
time is measured in ‘seconds’.
So, unit of power is joule per
second. This unit of power is
called ‘watt’.
i.e., 1 watt = 1 joule/1 second
One watt is a power of an agent
which does work at the rate:- 1
joule / second.
The bigger units of power are :
1 kilowatt=1000 watt or 1kW

67. commercial unit of energy
5/16/20
WORK AND ENERGY
67
Kilowatt hour (kWh) or 1 unit
The electrical energy used in
household, industries and
commercial establishment are
usually expressed in kilowatt
hour.
1 kWh is the energy used in 1
hour at rate of 1000 J/s or

68. 5/16/20
WORK AND ENERGY
68
1kWh = 1kW * 1h
= 1000 W * 3600
s
= 3600000 J
1kWh = 3.6 * 10^6 J
1 unit = 1 kilowatt
hour

69. 5/16/20
WORK AND ENERGY
69

70. 5/16/20
WORK AND ENERGY
70

71. 5/16/20
WORK AND ENERGY
71

72. 5/16/20
WORK AND ENERGY
72