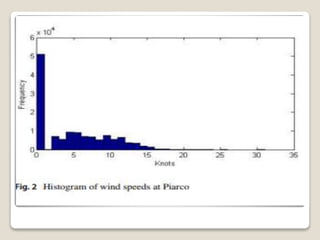
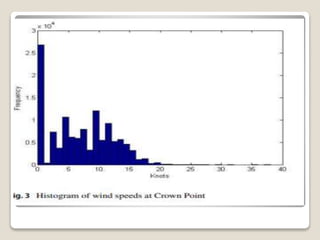
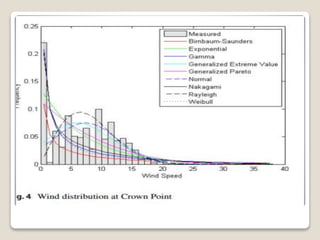
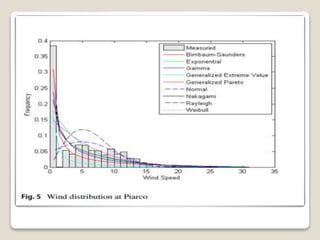
This document discusses different probability distributions that can be used to model wind speed data. It notes that the Weibull distribution is commonly used, but that other distributions like the generalized extreme value distribution, generalized Pareto distribution, Rayleigh distribution, autoregressive models, maximum entropy distributions, Nakagami distribution, normal distribution and exponential distribution have also been explored. The document aims to compare the performance of these distributions using goodness-of-fit tests and an application-specific information criteria method to identify the best distribution for wind energy applications. It then reviews the probability density functions for various candidate distributions considered.

1. Wind speed probability
distribution
Prepared by:-
Sonu kumar bairwa

2. introduction
 Many studies have aimed at
characterizing or comparing wind speed
distributions at different locations.
 Several emphasize seasonal variations
while diurnal variations have also been
examined .
 However, these have either been located
outside the Caribbean or have been
limited in their exploration of candidate
distributions.

3.  Furthermore, there is no consensus on
the goodness of ft criterion which is most
suitable for evaluating the appropriateness
of the distribution to a particular
application.
 The relative performance of these
distributions is compared using goodness
of ft tests.
 The concept of application-specific
information criteria (ASIC), is introduced
as an improved method for distribution
ranking in the case of wind energy studies.

4. Distribution fitting
 Typically, wind data is modelled as a
Weibull distribution, especially when the
aim is to characterise the annual
resource.
 For other applications such as statistical
analysis of extreme wind speeds, the
Weibull (or reverse Waybull) has also
been recommended while other
distributions such as the generalized
extreme value distribution and the
generalized pare to have been explored.

5.  Identifed the weakness of the Weibull
distribution as its failure to describe the
upper tail.
 The Rayleigh distribution has also been
used as a probability model for wind
speed , although some applications have
found Weibull to be more accurate .
 Recent studies found autoregressive
models and maximum entropy
distributions to be better suited to wind
speed applications than Weibull or
Rayleigh.

6.  Recent studies found autoregressive
models and maximum entropy
distributions to be better suited to wind
speed applications than Weibull or
Rayleigh.
 Alavi et al. found that the Nakagami
distribution performed well when
compared to other distributions frequently
used to model wind speed.

7.  Additionally, the Normal and Exponential
Distributions were identifed as potential
candidates via visual inspection of the
histogram shape.
 The Birnbaum–Saunders and Gamma
distributions performed well when
goodness of ft was assessed using the
Akaike information criterion (AIC) and the
Bayesian information criterion (BIC)
criteria, and were thus included in the
comparative analysis (Figs. 2, 3).

10. Review of probability distribution
functions
 The equations defining the probability
density functions (PDFs) for various
candidate distributions of interest are
given below. While by no means
exhaustive, the distributions represent
those commonly used in the literature.