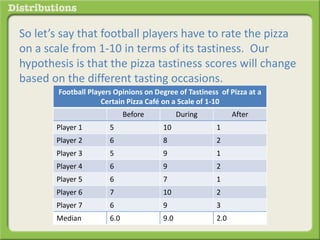
The Friedman test is a non-parametric statistical test that is used as an alternative to repeated measures ANOVA when the data is ordinal or not normally distributed. It compares the median values across three or more related groups or time points. Unlike ANOVA, it does not assume normal distribution of the data or equal intervals between ranks. The Friedman test determines if there are statistically significant differences in the distributions of a dependent variable among multiple groups or time points. It is appropriate to use when the underlying data is on an ordinal scale or highly skewed.

1. Friedman Test
The non-parametric analogue to the repeated
measures ANOVA is the Friedman test.

2. First let’s review what a repeated measures ANOVA is.

3. First let’s review what a repeated measures ANOVA.
A repeated measures ANOVA is used to determine if
there is a statistically significant difference between the
results of the same measure with the same group
across multiple occasions.

4. For example,
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1
Player 2
Player 3
Player 4
Player 5
Player 6
Player 7

5. Here is the fictitious data:
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1 5
Player 2 4
Player 3 3
Player 4 5
Player 5 4
Player 6 3
Player 7 4

6. Here is the fictitious data:
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1 5 14
Player 2 4 2
Player 3 3 3
Player 4 5 2
Player 5 4 1
Player 6 3 2
Player 7 4 3

7. Here is the fictitious data:
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1 5 14 2
Player 2 4 2 8
Player 3 3 3 9
Player 4 5 2 8
Player 5 4 1 7
Player 6 3 2 1
Player 7 4 3 8

8. Here is the fictitious data:
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1 5 14 2
Player 2 4 2 8
Player 3 3 3 9
Player 4 5 2 8
Player 5 4 1 7
Player 6 3 2 1
Player 7 4 3 8
Mean 3.9 3.4 6.9

9. *Note 1:
Remember that a Repeated Measures
ANOVA does not pin point which pair is
significantly different. It just let’s you
know that there is a difference. Post hoc
tests must be performed to determine
which pair is different.

10. *Note 2:
Because a pair-wise t-test is generally
used to determine if there is a difference
between two separate observation
occasions, the Repeated Measures
ANOVA is generally used with three or
more occasions even though it could be
used with just two.

11. The Friedman test is appropriate to use when the
underlying measurement is on an ordinal scale or the
distribution of a dependent variable is highly skewed.
The Friedman test will estimate whether there are
significant differences among distributions at multiple
(more than two) observation periods.

12. The Friedman test is appropriate to use when the
underlying measurement is on an ordinal scale or the
distribution of a dependent variable is highly skewed.
The Friedman test will estimate whether there are
significant differences among distributions at multiple
(more than two) observation periods.
While the Repeated Measures ANOVA compares group
means, the Friedman Test compares group medians.
Remember that a Median is less resistant to outliers

13. So let’s go back to our pizza-eating football player
example:
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1 5 14 2
Player 2 4 2 8
Player 3 3 3 9
Player 4 5 2 8
Player 5 4 1 7
Player 6 3 2 1
Player 7 4 3 8
Mean 3.9 3.4 6.9

14. Notice that the highlighted numbers are outliers in
each group which can skew the results for a Repeated
Measures ANOVA.
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1 5 14 2
Player 2 4 2 8
Player 3 3 3 9
Player 4 5 2 8
Player 5 4 1 7
Player 6 3 2 1
Player 7 4 3 8
Mean 3.9 3.4 6.9

15. Because the Median is less resistant to these outliers,
notice how the Median shows more of a separation
between these groups. The Median in this case may
reflect reality better than the Mean.
Number of Pizza Slices Eaten by a Group of Football Players
Before During After
Player 1 5 14 2
Player 2 4 2 8
Player 3 3 3 9
Player 4 5 2 8
Player 5 4 1 7
Player 6 3 2 1
Player 7 4 3 8
Mean 3.9 3.4 6.9
Median 4.0 2.0 8.0

16. Friedman test is also used when the data is rank
ordered or ordinal (no equal intervals).

17. So let’s say that football players have to rate the pizza
on a scale from 1-10 in terms of its tastiness. Our
hypothesis is that the pizza tastiness scores will change
based on the different tasting occasions.

18. So let’s say that football players have to rate the pizza
on a scale from 1-10 in terms of its tastiness. Our
hypothesis is that the pizza tastiness scores will change
based on the different tasting occasions.
Football Players Opinions on Degree of Tastiness of Pizza at a
Certain Pizza Café on a Scale of 1-10
Before During After
Player 1 5 10 1
Player 2 6 8 2
Player 3 5 9 1
Player 4 6 9 2
Player 5 6 7 1
Player 6 7 10 2
Player 7 6 9 3
Median 6.0 9.0 2.0

19. Once again the median is used here because on a scale
of 1-10 there is not an agreed upon definition usually
on how a 1 differs from a 2 compared to how a 7 differs
from an 8. Rating pizza taste is more subjective in
terms of how equal the intervals are compared to the
number of pizza slices which is a more objective
measure.

20. Once again the median is used here because on a scale
of 1-10 there is not an agreed upon definition usually
on how a 1 differs from a 2 compared to how a 7 differs
from an 8. Rating pizza taste is more subjective in
terms of how equal the intervals are compared to the
number of pizza slices which is a more objective
measure.
That is why in this case we would use a Friedman Test